随着人类对水资源利用程度的增长,水库修建深刻改变水沙条件,导致坝下游河床变形等响应性调整[1-2]. 大型水利工程蓄水运用后,坝下河段再造床过程中的河道冲淤调整是河床演变学、河流地貌学的研究重点之一. 由于水库调蓄方式、规模大小、河床边界条件不同,河道呈现出束窄、展宽、下切等差异性调整特征[3-5],而河床调整幅度、冲淤量大小及冲淤发展态势对于河势稳定、黄金水道建设、保障防洪安全等具有重要意义,沙量平衡分析是合理评估水库运行对坝下游河道演变影响的重要依据之一.
长江中下游宜昌至大通河段,属于大型冲积性平原河流. 受以三峡水库为核心的长江上游梯级水库群联合运用影响,中下游泥沙通量发生明显改变[6],打破了河道原有的冲淤相对平衡状态,入海泥沙来源由以上游来沙为主,变为中下游支流、湖泊来沙和河床冲刷补给占优. 董炳江等[7]基于实测资料,分析认为三峡水库坝下游冲刷逐渐向下游发展,城陵矶以下河段河床冲刷强度明显增大[8-9];另有部分研究提出,坝下游河道泥沙沿程恢复,冲刷将在长江中游城陵矶附近达到新的水沙平衡[10]. 目前,宜昌以下河段受长江上游水库群影响的范围、程度尚存在争议. 长江中下游沙量平衡分析是反映以三峡水库为核心的水利工程影响下河床调整态势、开展河道演变及整治研究的重要依据. 大型冲积河流河床由非均匀沙组成,但由于河道形态的多样性、河床组成的差异性、沿程支流水系入汇等因素的影响,沿程泥沙冲刷补给较为复杂[11]. 在河床冲刷与沙量恢复的过程中,各粒径组的输沙量均不会超出建库前水平,这是与河床边界、河型等因素无关的一般性规律[12]. 已有研究表明,三峡水库蓄水后细颗粒沙量在长江中游沿程缓慢恢复且恢复程度远小于蓄水前[13],粗颗粒沙量补给区域为宜昌至监利河段,其下游为淤积趋势[14]. 以上研究成果系统分析了长江中下游泥沙输移规律,但受三峡水库持续影响,坝下游冲刷强度明显向下游发展,不同时空尺度的分组泥沙冲淤特性有待进一步揭示.
沙量平衡法与断面地形法是计算泥沙冲淤量的两种主要方法. 沙量平衡法主要依据实测断面输沙量,认为河道冲淤量为进、出口断面输沙量差值,该方法的准确性主要取决于断面输沙量的测量精度. 断面地形法基于河道地形,断面间槽蓄量差值即为河道冲淤量. 安催花等[15]采用沙量平衡法和断面地形法分析计算了1960年以来黄河宁蒙河段的泥沙冲淤量,认为两种方法计算结果接近、各有特点,可互为补充. 段光磊等[16]、元媛等[17]认为沙量平衡法需考虑悬沙测验改正、泥沙测验定线误差、水量不平衡、河道采砂和分流洪道冲淤等;断面地形法需在弯道、汊道、河道急剧放宽和束窄的局部河段布置相对较密的断面. 这些工作较为详尽地阐述了沙量平衡法、断面地形法计算差异及其主要影响因素,但多集中在局部河段. 考虑上游梯级水库群联合调度影响范围广、作用时间长,本文选取长江中下游宜昌至大通河段为研究对象,收集了长江水利委员会所属干、支流主要水文站1950—2018年年径流量、输沙量及泥沙级配等实测水文数据,以及干流宜昌至大通河段1998—2018年河道地形和固定断面观测资料. 首先,基于大量实测资料,开展三峡水库蓄水运用以来长江中下游不同时空尺度、分组泥沙沙量平衡分析;其次,比较沙量平衡法、断面地形法计算差异,并从测量误差、断面代表性及断面间距带来的误差、河道采砂影响等多方面探讨产生差异的主要原因,以期加深对梯级水库群联合调蓄影响下坝下游河段冲淤规律的认识、为泥沙问题的研究提供参考.
1 研究区域及计算方法 1.1 研究河段长江中下游为冲积性平原河流,除宜昌至江口河段为砾卵石河床外,其他河段均以沙质河床为主. 河道两岸抗冲性较弱,但受两岸堤防和护岸等工程的控制作用,总体河势基本稳定. 受自然因素、水库群调蓄等人类活动影响,长江中下游江河湖库泥沙输移、交换及其驱动机制均十分复杂.
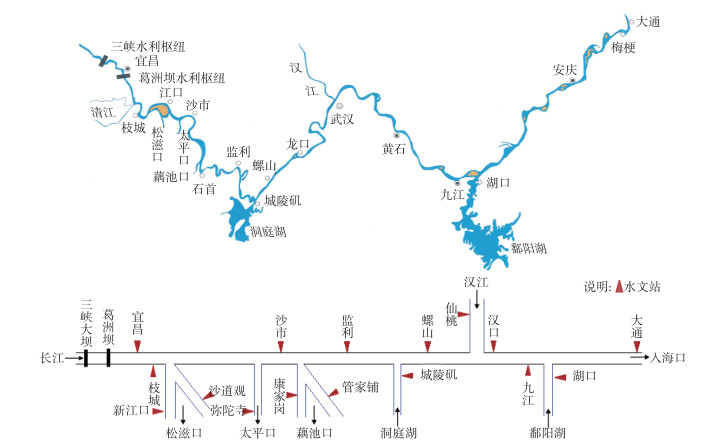
本文研究范围为长江中下游宜昌至大通长约1183 km的河道,其中宜昌至湖口为长江中游,长955 km,流域面积68万km2;湖口至大通为下游,长228 km. 长江中下游沿江两岸支流、湖泊众多,江湖关系复杂,主要包括清江、洞庭湖水系、汉江、鄱阳湖水系等,荆江南岸有松滋、太平、藕池、调弦四口分流入洞庭湖(调弦口于1959年建闸封堵),研究区域及长江中下游江湖关系见图 1.
|
图 1 研究区域示意图 Fig.1 Sketch of the study area |
沙量平衡法与河道地形法是计算冲淤量的常见方法. 沙量平衡法基于物质守恒定律,计算输入沙量与输出沙量的差值,作为该河段的冲淤量,该方法利用日均水文泥沙资料,在时间尺度上具备较好的连续性. 计算公式为:
| $ \Delta W = {W_1} - {W_2} + {E_1} - {E_2} $ | (1) |
式中,W1、W2分别代表进、出口输沙量;E1、E2分别为区间汇入、引出沙量;ΔW为河段冲淤量. 长江中下游宜昌至大通河段沙源较为复杂,包括干流进口沙量以及洞庭湖、鄱阳湖、汉江水系等区间支流湖泊来沙量;从河道输出沙量包括干流出口沙量以及松滋口、太平口、藕池口三口分流沙量.
断面地形法是利用河道地形计算冲淤量的方法之一,主要是基于固定断面或利用河道地形图沿程切割断面,计算河段内上、下断面过水面积,在空间尺度上具有较好的连续性,常采用截锥公式计算河段槽蓄量:
| $ V = \sum\limits_{i = 1}^{N - 1} {\frac{1}{3}({A_i} + {A_{i + 1}} + {\rm{ }}\sqrt {{A_i}\cdot{A_{i + 1}}} ){L_i}} $ | (2) |
式中,V代表河道槽蓄量(本文取平滩河槽);N为河段断面个数;Ai为第i个断面过水面积;Li为断面间距. 各测次之间的槽蓄量之差为河道冲淤量,即ΔV=V1-V2.
本文基于长江中下游干、支流水文站点泥沙输移量开展沙量平衡分析,对比沙量平衡法、断面地形法河道冲淤量计算结果,分析产生差异的主要原因. 由于沙量平衡法计算冲淤量以重量计,而断面地形法以体积计,文中按沙重1.35 t/m3进行换算. 此外,考虑到断面代表性及间距会对断面地形法计算精度产生影响,在主要原因分析中,局部河段断面地形法计算冲淤量结果与网格地形法进行对比,以合理评估断面布置带来的误差. 网格地形法主要利用河道地形实测点三维数据(x,y,z)或直接用GPS、全站仪、野外测量等提取实测地形三维数据,根据地形图测图比例尺大小或测点间距等确定适宜的网格尺寸,建立DEM数字高程模型,给定水位计算河道槽蓄量,两次测槽蓄量的差值即为河道冲淤量.
2 长江中下游沙量平衡分析 2.1 长江中下游泥沙沿程恢复以三峡水库为核心的梯级水库群陆续投运后,宜昌站下泄沙量大幅减少,长江中下游河道泥沙沿程补给. 但受水动力条件变化、河床组成差异性、河道形态多样性、通江湖泊以及支流入汇等多重因素的影响,泥沙恢复过程较为复杂.
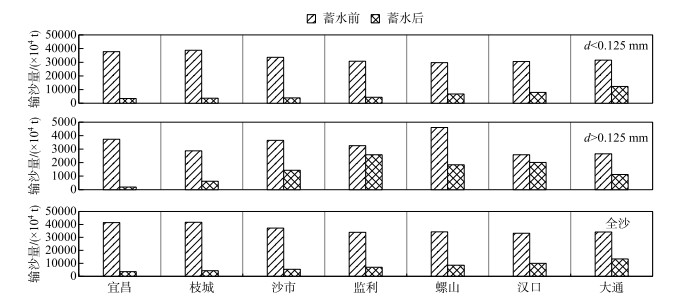
长江中下游干流主要控制站实测水沙资料表明,各粒径组输沙量均未恢复至蓄水前水平(图 2). 对于粒径d < 0.125 mm的悬移质细颗粒泥沙而言,其输沙量沿程递增,主要受河床补给与江湖入汇共同的影响[18]. 1987—2002年,宜昌、汉口、大通站d < 0.125 mm的悬移质泥沙年均输沙量分别为3.77亿、3.06亿和3.15亿t,三峡水库蓄水后2003—2018年三站年均输移量分别为0.34亿、0.79亿和1.23亿t,减幅为91 %、74 % 和61 %. 对于d>0.125 mm的悬移质粗沙部分而言,主要受坝下游河床冲刷补给影响,与蓄水前相比,宜昌、汉口和大通站年均粗沙输沙量减幅分别为95 %、22 % 和58 %,粗沙减幅明显小于全沙. 特别是2003—2008年,监利站年均粗沙输沙量为0.34亿t,已基本达到蓄水前多年平均值.
|
图 2 三峡水库蓄水前后长江中下游水文站点不同粒径组多年平均输沙量 Fig.2 Average annual sediment transport of different diameter groups at hydrological stations in the middle and lower reaches of the Yangtze River before and after the impoundment of the Three Gorges Reservoir |
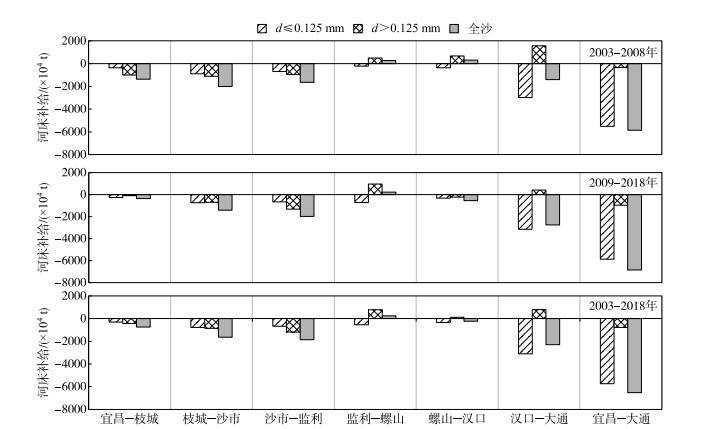
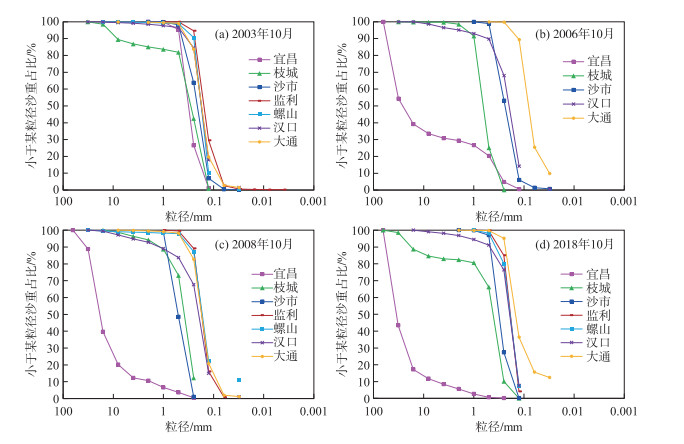
不同粒径组泥沙恢复距离存在差异,细颗粒恢复距离较长,而粗颗粒恢复距离相对较短. 三峡水库蓄水后的2003—2018年,宜昌至监利河段细、粗颗粒泥沙均呈冲刷态势,年均冲刷量分别为0.18亿和0.25亿t,以粗沙冲刷为主;监利至大通河段细沙年均冲刷0.40亿t,而粗沙落淤0.17亿t,表现为“冲细淤粗”的现象(图 3). 一方面,从河流泥沙基本理论来看,河床中细颗粒泥沙相对于粗颗粒更易起动;另一方面,河床补给是泥沙沿程恢复的主要来源,长江中下游河床组成自上而下逐渐细化,表现出冲积河流的一般特点. 各站点级配曲线表明(图 4),宜昌至沙市站河床组成以粒径d>0.125 mm的粗沙为主,且随着水库蓄水运行时间的增长,河床呈粗化态势,而下游监利至大通站粒径d < 0.125 mm细沙百分含量相对较大,细颗粒在河床中所占比例沿程增加,为长距离细颗粒冲刷恢复提供了来源.
|
图 3 2003—2018年长江中下游各区间河段不同粒径组年均河床泥沙补给量 Fig.3 Average annual sediment replenishment of different diameter groups from river bed in the middle and lower reaches of the Yangtze River from 2003 to 2018 |
|
图 4 长江中下游水文站床沙颗粒级配变化 Fig.4 Changes of bed material grading at hydrological stations in the middle and lower reaches of the Yangtze River |
随着三峡水库蓄水运行时间的增长,粗沙主要冲刷补给带有所下移. 2003—2008年,宜昌至沙市河段粗沙年均冲刷量为0.21亿t,是粗沙的主要补给区域. 受清水冲刷砂卵石河床粗化的影响(图 4),三峡水库175 m试验性蓄水后,宜昌至枝城河段床沙明显粗化,对该组分泥沙的补给程度减弱,枝城至沙市河段粗沙年均补给量由0.11亿t降低至0.07亿t,粗沙主要冲刷补给带下移至沙市至监利河段,该河段粗沙年均补给量增加近0.04亿t,冲刷逐步向下游发展.
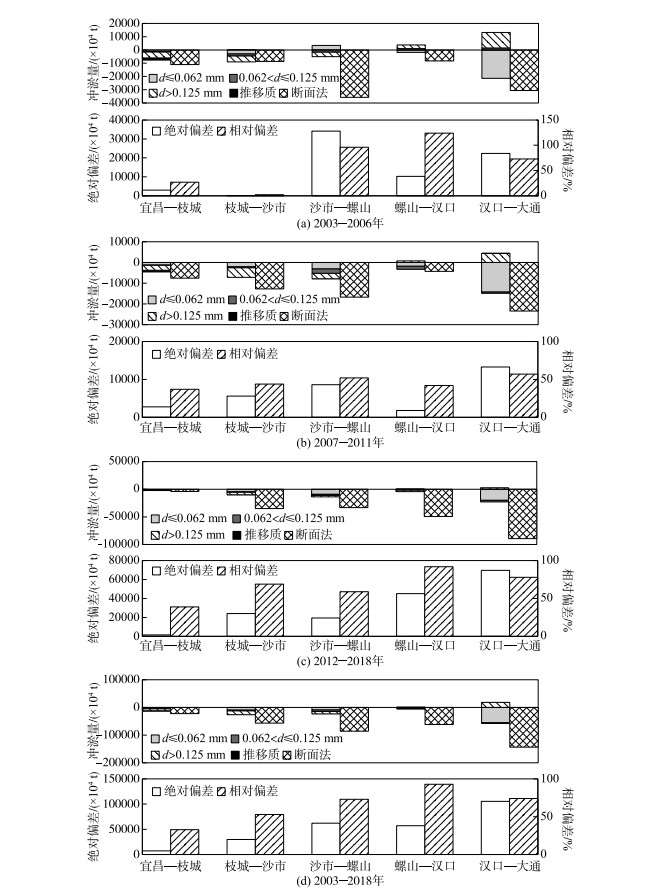
2.2 长江中下游沙量平衡分析 2.2.1 沿程变化三峡水库蓄水后,长江中下游出现了长时间、长距离的响应性冲淤调整. 沿程各区间河段冲淤量计算成果表明(图 5),2003—2018年,以沙市为界,距离坝址较近的宜昌至枝城、枝城至沙市河段两方法计算绝对差值分别为0.73亿和2.98亿t,而沙市至螺山、螺山至汉口、汉口至大通河段计算绝对差值达到了6.22亿、5.72亿和10.54亿t(由于城陵矶以下河段2002年10月无固定断面数据,沙市至大通河段沙量平衡法及断面地形法计算年份为2002—2018年,下同),沙市至大通河段是长江中下游宜昌至大通长河段计算偏差的主要来源,占比高达86 %. 考虑到在河段长度方面,沙市以上河段河长较短,仅占宜昌至大通河段全长的14 %,而沙市至螺山、螺山至汉口、汉口至大通河段河长占比分别为23 %、18 % 和45 %,其中,河长占比最高的汉口至大通河段也是两方法计算绝对偏差最大的河段,河段长度越长,产生的累积偏差也会越大. 各河段单位河长冲淤量绝对偏差表明,2003—2018年,宜昌至枝城、枝城至沙市、沙市至螺山、螺山至汉口、汉口至大通河段计算绝对差值分别为124万、338万、234万、274万和206万t/km,相对而言,枝城至沙市河段单位河长绝对差值较大.
|
图 5 长江中下游各区间河段沙量平衡法与断面地形法计算结果对比(冲淤量计算中“-”为冲刷,“+”为淤积;绝对偏差=沙量平衡法计算冲淤量—断面地形法计算冲淤量,相对偏差=绝对偏差/断面地形法计算冲淤量的绝对值;由于城陵矶以下河段2002年10月无固定断面数据,沙市至大通河段沙量平衡法及断面地形法计算年份为2002—2018年,下同) Fig.5 Comparison of the calculation results between sediment balance method and the section topographical method of each reach in the middle and lower reaches of the Yangtze River |
以三峡水库蓄水初期、金沙江下游溪洛渡向家坝水电站陆续投运为界,在时间尺度上划分为2003—2006、2007—2011、2012—2018年3个时段. 宜昌至枝城河段河床冲刷量逐步减少,而枝城至沙市河段冲刷量增大,冲刷逐步向下游发展. 两河段沙量平衡法与断面地形法计算绝对偏差与冲刷量变化趋势基本一致,而相对偏差均呈逐时段增大态势,至2012—2018年,宜昌至枝城、枝城至沙市河段相对偏差分别达39 %、69 %;沙市至螺山、螺山至汉口、汉口至大通河段2007—2011年沙量平衡法与断面地形法计算相对偏差较小,在50 % 左右,而2003—2006、2012—2018年相对偏差较大,特别是在三峡水库蓄水初期(2003—2006年),沙量平衡法计算螺山至汉口河段呈淤积态势,而断面地形法计算该河段以冲刷为主,两方法定性上出现了相反的结果,相对偏差达124 %.
2.2.3 不同粒径泥沙平衡分析从不同粒径组泥沙冲淤来看,宜昌至大通长河段以悬移质中粒径d≤0.062 mm的泥沙冲刷为主,2003—2018年,该粒径组泥沙累计冲刷8.22亿t,占全沙冲刷量的近76 %,且绝大部分来源于汉口至大通河段.
对于悬移质而言,宜昌至枝城、枝城至沙市以及沙市至螺山河段粗、细沙均呈冲刷态势,其中,距离坝址较近的宜昌至枝城、枝城至沙市河段以粒径d>0.125 mm的粗沙以冲刷为主,粗沙冲刷量分别为0.70亿、1.37亿t,占比分别达悬移质输沙量的58.3 %、52.0 %;相对而言,沙市至螺山河段细沙冲刷量占比增大而粗沙占比减小,2003—2018年,粒径d≤0.125 mm的细沙冲刷为1.46亿t,占比达62.9 %. 螺山至汉口、汉口至大通河段细沙冲刷而粗沙落淤,粒径d≤0.125 mm的泥沙冲刷量是沙量平衡法计算河道冲淤量的主要影响因素,以汉口至大通河段为例,2003—2018年,该河段悬移质泥沙冲刷量为3.91亿t,其中,粒径d≤0.125 mm的泥沙冲刷量近5.56亿t,是汉口至大通河段的主要冲刷粒径组.
对于推移质而言,三峡水库蓄水后,距坝址较近的宜昌至枝城河段推移质冲刷量最大,达0.33亿t,随距坝址距离的增加,推移质冲刷量逐步减少,直至汉口至大通河段,推移质落淤0.12亿t,相对而言,推移质冲淤量占全沙冲淤的比例较小.
总体来看,在沿程变化方面,沙市至大通河段是长江中下游沙量平衡法与断面地形法计算偏差的主要来源,占比高达86 %,而单位河长冲淤量绝对偏差以枝城至沙市河段最大;在沿时变化方面,宜昌至沙市河段计算相对偏差均呈逐时段增大态势,沙市至大通河段2003—2006、2012—2018年两时段计算相对偏差较大;在不同粒径泥沙冲淤方面,粒径d≤0.125 mm的泥沙冲刷量是沙量平衡法计算河道冲淤的主要影响因素.
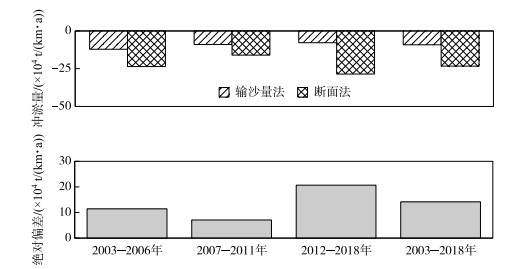
从三峡水库蓄水后长江中下游宜昌至大通全河段冲淤量计算成果来看,2003—2018年,沙量平衡法、断面地形法计算结果表明,宜昌至大通河段冲刷量分别为10.76亿和36.95亿t,两者定性一致,但定量上相差71 % (表 1). 单位河长年均冲淤量计算结果表明,2003—2018年沙量平衡法与断面地形法绝对偏差为14.17万t/(km·a),其中,2012—2018年年均计算绝对偏差较大,为20.72万t/(km·a)(图 6).
| 表 1 2003—2018年长江中下游宜昌至大通河段沙量平衡法与断面地形法计算结果对比 Tab. 1 Comparison of the calculation results between sediment balance method and topography method from Yichang to Datong in the middle and lower reaches of the Yangtze River from 2003 to 2018 |
|
图 6 不同时段长江中下游宜昌至大通河段单位河长沙量平衡法与断面地形法年均计算结果对比 Fig.6 Comparison of the average annual calculation results between sediment balance method and the section topographical method of Yichang to Datong per unit length in different periods |
沙量平衡法反映了整个河段的综合冲淤情况,而断面地形法体现了不同计算水位下河槽的冲淤量,若考虑各自误差的影响,对于同一河段在相同时段内,理论上沙量平衡法与断面地形法计算的冲淤量应相等或大致相同[19]. 三峡水库运用以来长江中下游冲淤计算结果表明,宜昌至大通河段沙量平衡法与断面地形法计算相对偏差为71 %,距离三峡大坝较近的宜昌至沙市河段两方法计算偏差小,而沙市至大通河段偏差较大,单位河长绝对偏差以枝城至沙市河段最大. 可以看出,由于水文泥沙及河道地形测量误差、断面布置、河道采砂影响等,两种方法的计算成果在定量上存在一定差异,局部河段甚至在定性上出现相反的结果,这将会对长江泥沙冲淤特性的分析与研究、三峡水库的优化调度及安全运行产生极大的影响. 因此,本文进一步探讨沙量平衡法与断面地形法计算河道冲淤量产生差异的主要原因.
3.1 测量误差由于水文泥沙测验和地形测量技术的限制,河道地形测量和水文泥沙测验所依据的规范和标准不同,可能会导致出现不同的测量精度和误差,测量误差是沙量平衡法与断面地形法计算河床冲淤量产生差异的原因之一.
3.1.1 泥沙测量误差(1) 悬移质输沙量测验准确度:对于悬移质测验而言,由于悬移质含沙量沿断面的纵、横向分布的复杂性和取样仪器、测验方法、水样处理等的局限性,综合测验误差大于流量测验误差. 根据现行的悬移质泥沙测验规范,一类站输沙率成果的允许随机不确定度为17.7 %,允许系统误差为3 %. 若按长江中游宜昌站2003—2018年多年平均输沙量为0.36亿t计,系统误差量可达0.01亿t.
(2) 悬移质输沙量测验误差分析:沙量平衡法利用进、出沙量计算河道冲淤量. 影响悬移质输沙量精度的因子主要有临底悬沙测验误差、单—断沙关系误差等:
① 临底悬沙测验误差:对于悬移质泥沙测验而言,根据测量规范要求,测量范围在距离河底0.2倍水深以上,对于0.2倍水深以下的临底层泥沙尚未施测. 从断面含沙量沿垂线分布来看,从水面到河底含沙量逐渐增大,且在三峡水库蓄水后粗颗粒泥沙百分含量增大,近底含沙量明显大于垂线平均含沙量,该部分缺少测量会对沙量平衡法计算河道冲淤量产生影响. 2006年以来长江水利委员会水文局首先在三峡水库进出库5个水文站(含枝城、沙市、监利三站)开展临底悬沙试验研究,对悬移质输沙进行了相应的改正[20],其中沙市站临底悬沙对输沙量冲刷量的改正比例为13.2 %.
韩其为[21]根据理论分析认为,粗颗粒悬移质在长江中游绝大部分集中于离河底相对深η=0.1~0.2以下的近底部分,粒径在0.50~1.00 mm之间的颗粒在荆江输沙量约81 % 集中于η=0.1以下,而对于城汉河段可能达到92 %. 对于荆江平均床沙质条件(0.25~0.5 mm及λ=9.68)到两点法和三点法(1∶1∶1)的误差为7.4 % 和26.7 %. 从长时空尺度来看,宜昌站悬沙改正率很小,可忽略不计,若大通站悬沙改正率按26.7 % 计,则三峡水库蓄水后的2003—2018年,大通站悬沙改正后输沙量增加近6.46亿t,宜昌至大通河段沙量平衡法与断面地形法计算相对误差可由71 % 减小至53 %.
② 单—断沙关系带来的误差:断面平均含沙量常与断面上某一测点含沙量或某一垂线平均含沙量有一定关系. 单断沙关系的相关性强弱与测验河段平面形态、断面形态和测验断面河床冲淤等有关,根据段光磊统计结果[22],2003—2008年监利站单沙取样代表性很好,而沙市站断沙比单沙偏大,悬移质输沙量改正系数为0.973. 对于沙市至螺山河段而言,若三峡水库蓄水后的2002—2018年沙市站悬移质输沙量改正系数按0.973计,经修正后的沙市至螺山河段沙量平衡法计算冲刷量增加0.298亿t,与断面地形法相比,相对偏差可由73 % 减少至69 %,差值进一步缩小.
3.1.2 河道地形测点高程误差测点高程主要受推算的水位精度及回声仪测深精度的影响. 其中,水位精度包括代表性误差、观读误差与推算模型误差等;而水深测量的关键在于测深仪对地形观测的适应性.
3.2 断面代表性及断面间距断面地形法是利用河道地形观测资料,按断面切割法或地形图量算法计算河段的冲淤量. 断面地形法计算冲淤量的关键因素是河道槽蓄量计算误差的大小,断面间槽蓄量计算主要采取椎体法,截锥公式有严格立体几何定义的公式,要求两底面平行且相似,然而实际河道中固定断面测量工作量大,断面布设不可能足够密集,断面代表性及其间距会对断面地形法计算精度产生影响. 特别是三峡水库蓄水后下荆江急弯段出现了“切滩撇弯”的新现象[23-24], 城陵矶以下分汊河段表现出“主长支消”和“主消支长”并存的分异性规律[25-26],而以往固定断面多依据水库蓄水前弯曲河段凹岸侧普遍冲刷、分汊河段主支汊冲淤交替等演变特征布设,断面布置能否反映蓄水后河道冲淤变化特性也将直接影响到河道冲淤量的计算结果. 因此,进一步对比断面地形法与网格地形法计算冲淤量结果,以合理评估断面布置产生的误差.
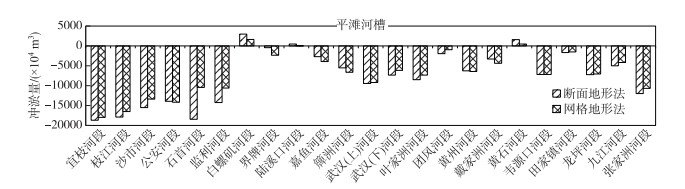
对于长江中下游河段而言,2002—2018年宜昌至湖口河段采用1∶5000实测固定断面,共有断面578个,断面间距平均约为1.5 km. 从断面地形法计算结果来看,1998—2013年三峡水库下游宜昌至湖口河段平滩河槽冲刷量为17.1801亿m3,网格地形法计算冲刷量相对较小,为15.8627亿m3,绝对偏差仅占该河段平滩河槽槽蓄量的0.68 %,计算相对偏差在8.3 % 左右(表 2). 以上结果表明,目前宜昌—湖口河段由于断面布置及间距引起的计算误差较小、精度较高,固定断面的布设能较好地反映河床冲淤特性(图 7).
| 表 2 1998—2013年三峡水库下游宜昌至湖口河段断面地形法与网格地形法平滩河槽冲淤量计算结果对比 Tab. 2 Comparison of the bankfull channel erosion and deposition amount between the section topographical method and the grid topographical method in the Yichang to Hukou reaches downstream of the Three Gorges Reservoir from 1998 to 2013 |
|
图 7 1998—2013年三峡水库下游宜昌至湖口各区间河段平滩河槽冲淤量 Fig.7 The amount of erosion and deposition of the bankfull channel in the Yichang to Hukou reaches downstream of the Three Gorges Reservoir from 1998 to 2013 |
湖口至大通河段采用1∶10000实测地形图切割断面,断面间距平均约为2 km. 从湖口至大通河段断面地形法与网格地形法计算结果对比来看,1998—2016年,断面地形法计算该河段冲刷泥沙3.2393亿m3,与网格地形法相比计算冲刷量偏大,相对误差达23.5 %. 其中,2011—2016年,断面地形法计算河段冲刷量为2.1569亿m3,与网格地形法相比,绝对偏差为0.7751亿m3,相对偏差高达56.1 % (表 3). 相对于宜昌至湖口河段而言,一方面,湖口至大通河段冲淤幅度较小,计算相对偏差较高;另一方面,该河段断面平均间距在2 km左右,与宜昌至湖口河段相比,断面布置较为稀疏,由于断面布置及间距引起的计算误差较大.
| 表 3 三峡水库下游湖口至大通河段断面地形法与网格地形法平滩河槽冲淤量计算结果对比 Tab. 3 Comparison of the bankfull channel erosion and deposition amount between the section topographical method and the grid topographical method in the Hukou to Datong reaches downstream of the Three Gorges Reservoir |
三峡水库蓄水后2002—2018年,沙量平衡法计算宜昌至大通河段冲刷泥沙10.76亿t,若采用网格地形法计算,即在断面地形法计算的基础上,宜昌至湖口河段相对偏差按8.3 % 计,湖口至大通河段相对偏差按23.5 % 计,则沙量平衡法与网格地形法绝对偏差可减小约3.95亿t,相对偏差由71 % 减少至67 %.
从长江中下游各区间河段统计结果来看,对于宜昌至湖口河段而言,断面地形法与网格地形法计算差异最大的河段位于沙市至螺山河段,相对偏差达30 %,该河段多以分汊、弯曲河型为主,深泓走向曲折多变,两个相邻常测固定断面夹角往往很大,误差最为显著的石首河段、监利河段等均为典型的弯曲分汊河型,石首河段绝对偏差达8023万m3,相对偏差在77 % 左右. 若采用网格地形法计算沙市至螺山河段冲淤量(在断面地形法计算的基础上,沙市至螺山河段相对偏差按30 % 计),三峡水库蓄水后2003—2018年,沙量平衡法与网格地形法计算绝对偏差减少近40 %,相对偏差可由73 % 减少至61 %. 对于湖口至大通河段而言,断面地形法与网格地形法相比,计算差异最大的河段为马垱河段(图 8),从平面形态来看,马垱河段为微弯分汊河型,河道多级分汊,江心搁排洲滩体规模较大,1998—2016年,两方法计算该河段绝对偏差为5634万m3,相对偏差高达339 %. 可见,对于局部河段而言,断面间距大、弯曲、分汊河型等断面代表性较差,常测固定断面控制不了地形变化,特别是弯曲分汊河段,断面地形法计算河道冲淤量时会存在一定的误差.

|
图 8 1998—2016年及2011—2016年三峡水库下游湖口至大通各区间河段平滩河槽冲淤量 Fig.8 The amount of erosion and deposition of the bankfull channel in the Hukou to Datong reaches downstream of the Three Gorges Reservoir from 1998 to 2016 and 2011 to 2016 |
河砂是宝贵的自然资源,也是长江沿线基础设施建设的重要来源之一,为满足工业需求,长江干流已大量开采砂石料. 人类活动影响中,河道采砂是沙量平衡法与断面地形法计算河道冲淤量产生差异的主要原因之一.
对于长江中下游河段而言,坝下游宜昌至大通河段以冲刷为主,断面地形法计算的冲刷量大于沙量平衡法,相对误差绝对值在2 % ~124 % 之间. 从人类活动采砂影响来看,干流采砂规划共计3轮:第1轮采砂规划期为2002—2010年,规划对象为建筑砂料开采,年度采砂控制总量为3400万t;第2轮采砂规划期为2011—2015年,规划对象包括建筑砂料开采及吹填等其他砂料开采,其中吹填造地主要发生在大通以下河段,建筑砂料年度控制开采总量为1940万t;第3轮采砂规划期为2016—2020年,建筑砂料年度控制开采总量为1730万t,较上轮规划减少210万t.
《长江泥沙公报》数据统计表明,2004—2015年长江中游干流湖北、江西、安徽等3省经许可实施的采砂总量为1.312亿t(合0.905亿m3),约占宜昌至湖口河段平滩河槽累积冲刷量的6.2 %. 2012年以后河道采砂主要集中在长江下游的安徽、江苏和上海等省(市).
另外,由于非法采砂活动猖獗,长江中下游河道实际采砂量更大. 据不完全调查统计,本属于禁采区的宜昌至沙市河段2003—2009年采砂总量约为7140万t,为同期实测河床冲刷量的20 % 左右;2012—2014年采砂总量约为1820万t,平均年开采量在600万t左右. 采用沙量平衡法计算宜昌至沙市河段冲淤量,2003—2009年、2012—2014年分别冲刷22407万和6354万t;断面地形法计算的冲刷量分别为28838万和18527万t,沙量平衡法与断面地形法计算相对误差分别为22.3 % 和65.7 %,若考虑采砂影响,则修正后的断面地形法计算宜昌至沙市河段冲刷泥沙分别为21698万和16707万t,两方法计算相对误差降低至3.2 % 和62.0 %. 整体来看,对于宜昌至沙市河段而言,2003—2018年沙量平衡法和断面地形法计算冲淤量分别为4.18亿和7.89亿t,相对误差为47.0 %,若考虑采砂影响及临底悬沙测验误差,其中河道采砂量占实测河床冲刷量的比例约为20 %,宜昌站悬沙改正率很小,可忽略不计,松滋口、太平口、沙市站临底悬沙对输沙量的改正比例为13.2 % ~26.7 % (平均约20 % 计),则修正后的沙量平衡法、断面地形法计算宜昌至沙市河段冲刷泥沙分别为6.09亿和6.31亿t,两方法计算相对误差降低至3.5 %,吻合相对较好.
4 结论1) 以三峡水库为核心的梯级水库群蓄水拦沙运用导致长江中下游出现了长时间、长距离的冲刷调整. 沙量平衡分析表明,2003—2018年宜昌至大通河段冲刷泥沙10.76亿t(含推移质泥沙冲刷0.26亿t),其中粒径小于0.125 mm的泥沙冲刷约9.54亿t,占悬移质泥沙总冲刷量的90.9 %. 河床沿程冲刷补给作用明显,以螺山为界,宜昌至螺山段“粗细均冲”,螺山至大通河段则“细冲粗淤”.
2) 宜昌至大通河段2003—2018年沙量平衡法与断面地形法计算的冲淤量分别为10.76亿和36.95亿t,计算结果定性一致,相对偏差为71 %. 从沿程差异分布来看,距离三峡大坝坝址较近的宜昌至沙市河段两方法计算绝对差值较小,而沙市至大通河段差值较大,占宜昌至大通全河段绝对偏差的近86 %. 河段长度越长,产生的累积偏差也会越大,2003—2018年,宜昌至枝城、枝城至沙市、沙市至螺山、螺山至汉口、汉口至大通河段单位河床计算绝对差值分别为124万、338万、234万、274万和206万t/km,枝城至沙市河段偏差较大.
3) 宜昌至沙市河段沙量平衡法和断面地形法计算结果分别为4.18亿和7.89亿t,河道采砂量约占实测河床冲刷量的20 %,临底悬沙对输沙量冲刷量的改正比例为13.2 % ~26.7 % (平均约为20 %). 修正后,两方法计算结果吻合相对较好. 沙市至大通河段相差较大,泥沙测验、固定断面布设、河道采砂等是导致沙量平衡法与断面地形法出现差异的主要原因.
| [1] |
Williams GP, Wolman MG eds. Downstream effects of dams on alluvial rivers. United States Geological Survey Professional Paper 1286. Washington: United States Government Printing Office, 1984.
|
| [2] |
Yang SL, Milliman JD, Xu KH et al. Downstream sedimentary and geomorphic impacts of the Three Gorges Dam on the Yangtze River. Earth-Science Reviews, 2014, 138: 469-486. DOI:10.1016/j.earscirev.2014.07.006 |
| [3] |
Smith ND, Morozova GS, Pérez-Arlucea M et al. Dam-induced and natural channel changes in the Saskatchewan river below the E.B. Campbell Dam, Canada.. Geomorphology, 2016, 269: 186-202. DOI:10.1016/j.geomorph.2016.06.041 |
| [4] |
Scorpio V, Rosskopf CM. Channel adjustments in a Mediterranean River over the last 150 years in the context of anthropic and natural controls. Geomorphology, 2016, 275: 90-104. DOI:10.1016/j.geomorph.2016.09.017 |
| [5] |
Xia JQ, Deng SS, Zhou MR et al. Effects of the Three Gorges Project operation on the recent variation in bankfull channel geometry of the Jingjiang Reach. Advances in Water Science, 2016, 27(3): 385-391. [夏军强, 邓珊珊, 周美蓉等. 三峡工程运用对近期荆江段平滩河槽形态调整的影响. 水科学进展, 2016, 27(3): 385-391.] |
| [6] |
Yang YP, Zhang MJ, Li YT et al. Suspended sediment recovery and bed sand compensation mechanism affected by the Three Gorges Project. Acta Geographica Sinica, 2016, 71(7): 1241-1254. [杨云平, 张明进, 李义天等. 长江三峡水坝下游河道悬沙恢复和床沙补给机制. 地理学报, 2016, 71(7): 1241-1254. DOI:10.11821/dlxb201607012] |
| [7] |
Dong BJ, Xu QX, Yuan J et al. Mechanism of serious scour along the downstream of Three Gorges Reservoir in recent years. Journal of Sediment Research, 2019, 44(5): 42-47. [董炳江, 许全喜, 袁晶等. 近年来三峡水库坝下游河道强烈冲刷机理分析. 泥沙研究, 2019, 44(5): 42-47.] |
| [8] |
Sun QH, Xia JQ, Zhou MR et al. Characteristics of channel adjustments and bank erosion in the Chenghan reach after the Three Gorges Project operation. J Lake Sci, 2019, 31(5): 1447-1458. [孙启航, 夏军强, 周美蓉等. 三峡工程运用后城陵矶-武汉河段河床调整及崩岸特点. 湖泊科学, 2019, 31(5): 1447-1458. DOI:10.18307/2019.0526] |
| [9] |
Zhang W, Wu MQ, Li SX et al. Mechanism of adjustment of scouring and silting of Chenglingji-Jiujiang reach in the middle reaches of the Yangtze River after impoundment of the Three Gorges Dam. Advances in Water Science, 2020, 31(2): 162-171. [张为, 吴美琴, 李思璇等. 三峡水库蓄水后城陵矶至九江段河道冲淤调整机理. 水科学进展, 2020, 31(2): 162-171.] |
| [10] |
Lai X, Yin D, Finlayson BL et al. Will river erosion below the Three Gorges Dam stop in the middle Yangtze?. Journal of Hydrology, 2017, 554: 24-31. DOI:10.1016/j.jhydrol.2017.08.057 |
| [11] |
Dai SB, Lu XX. Sediment load change in the Yangtze River (Changjiang): A review. Geomorphology, 2014, 215: 60-73. DOI:10.1016/j.geomorph.2013.05.027 |
| [12] |
Chen F, Li YT, Tang JW et al. Analysis of group-sized sediment transport downstream a reservoir. Journal of Hydroelectric Engineering, 2010, 29(1): 164-170. [陈飞, 李义天, 唐金武等. 水库下游分组沙冲淤特性分析. 水力发电学报, 2010, 29(1): 164-170.] |
| [13] |
Guo XH, Li YT, Qu G et al. Analysis of sediment transport in Middle Yangtze River after filling of the Three Gorges Reservoir. Journal of Sediment Research, 2014(5): 11-17. [郭小虎, 李义天, 渠庚等. 三峡工程蓄水后长江中游泥沙输移规律分析. 泥沙研究, 2014(5): 11-17.] |
| [14] |
Yang YP, Zhang MJ, Li SZ et al. Transport patterns of the coarse and fine sediments and its causes in the downstream of the Three Gorges Dam. J Lake Sci, 2017, 29(4): 942-954. [杨云平, 张明进, 李松喆等. 三峡大坝下游粗细颗粒泥沙输移规律及成因. 湖泊科学, 2017, 29(4): 942-954. DOI:10.18307/2017.0418] |
| [15] |
An CH, Lu J, Qian Y et al. Spatial-temporal distribution characteristic and course of sedimentation in the Ningxia-Inner Mongolia reaches of the Yellow River. Journal of Hydraulic Engineering, 2018, 49(2): 195-206, 215. [安催花, 鲁俊, 钱裕等. 黄河宁蒙河段冲淤时空分布特征与淤积原因. 水利学报, 2018, 49(2): 195-206, 215.] |
| [16] |
Duan GL, Peng YB, Guo MJ. Comparative analysis on riverbed erosion and deposition amount calculated by different methods. Journal of Yangtze River Scientific Research Institute, 2014, 31(2): 108-113, 118. [段光磊, 彭严波, 郭满姣. 河道实测冲淤量不同计算方法结果比较分析. 长江科学院院报, 2014, 31(2): 108-113, 118. DOI:10.3969/j.issn.1001-5485.2014.02.021] |
| [17] |
Yuan Y, Zhang XF, Duan GL. Reasonable profile spacing in calculation of channel scour and silting amount of Yichang-Zhicheng river reach by cross-section method. Engineering Journal of Wuhan University, 2014, 47(2): 149-155. [元媛, 张小峰, 段光磊. 断面法计算宜昌至枝城河段河道冲淤量的合理间距. 武汉大学学报: 工学版, 2014, 47(2): 149-155.] |
| [18] |
Guo XH, Qu G, Liu Y et al. Sediment transport of different particle size groups in the downstream channel after operation of the Three Gorges Project. J Lake Sci, 2020, 32(2): 564-572. [郭小虎, 渠庚, 刘亚等. 三峡工程运用后坝下游河道泥沙输移变化规律. 湖泊科学, 2020, 32(2): 564-572. DOI:10.18307/2020.0226] |
| [19] |
Shu CW, Tan GM. Advances in calculation methods for river sedimentation. Journal of Sediment Research, 2009(4): 68-73. [舒彩文, 谈广鸣. 河道冲淤量计算方法研究进展. 泥沙研究, 2009(4): 68-73. DOI:10.3321/j.issn:0468-155X.2009.04.012] |
| [20] |
Bureau of Hydrology, Changjiang Water Resources Commission ed. Analysis of the unbalanced sediment transport downstream of the Three Gorges Reservoir in 2017. Wuhan: Bureau of Hydrology, Changjiang Water Resources Commission, 2018. [长江水利委员会水文局. 2017年度长江三峡工程水文泥沙观测三峡水库坝下游不平衡输沙分析. 武汉: 长江水利委员会水文局, 2018. ]
|
| [21] |
Han QW. Error analysis of coarse suspended load measuring. Journal of China Hydrology, 2008, 28(1): 1-6, 20. [韩其为. 粗颗粒悬移质测验误差分析. 水文, 2008, 28(1): 1-6, 20.] |
| [22] |
Duan GL. Study on the different computation patterns on riverbed erosion and deposition amount [Dissertation]. Wuhan: Wuhan University, 2012. [段光磊. 冲积河流冲淤量计算模式研究[学位论文]. 武汉: 武汉大学, 2012. ]
|
| [23] |
Fan YY, Zhang W, Han JQ et al. The typical meandering river evolution adjustment and its driving mechanism in the downstream reach of TGR. Acta Geographica Sinica, 2017, 72(3): 420-431. [樊咏阳, 张为, 韩剑桥等. 三峡水库下游弯曲河型演变规律调整及其驱动机制. 地理学报, 2017, 72(3): 420-431. DOI:10.11821/dlxb201703005] |
| [24] |
Zhu LL, Xu QX, Xiong M. Fluvial processes of meandering channels in the Lower Jingjiang River reach after the impoundment of Three Gorges Reservior. Advances in Water Science, 2017, 28(2): 193-202. [朱玲玲, 许全喜, 熊明. 三峡水库蓄水后下荆江急弯河道凸冲凹淤成因. 水科学进展, 2017, 28(2): 193-202.] |
| [25] |
Han JQ, Zhang W, Yuan J et al. Responses of riverbed morphology to the hydrological regime in anabranching reaches of the downstream Three Gorges Reservoir. Advances in Water Science, 2018, 29(2): 186-195. [韩剑桥, 张为, 袁晶等. 三峡水库下游分汊河道滩槽调整及其对水文过程的响应. 水科学进展, 2018, 29(2): 186-195.] |
| [26] |
Zhu LL, Ge H, Li YT et al. Branching channels in the middle Yangtze River, China. Journal of Basic Science and Engineering, 2015, 23(2): 246-258. [朱玲玲, 葛华, 李义天等. 三峡水库蓄水后长江中游分汊河道演变机理及趋势. 应用基础与工程科学学报, 2015, 23(2): 246-258.] |
 2021, Vol. 33
2021, Vol. 33 

