(2: 江苏省水利厅, 水土保持生态环境监测总站, 南京 210029)
(2: Soil and Water Conservation Ecological Environment Monitoring Station, Water Resources Department of Jiangsu Province, Nanjing 210029, P. R. China)
水库按其所在位置和形成条件,通常分为山谷水库、平原水库和地下水库3种类型,而我国大部分水库属山谷型水库. 大型过水性湖泊作为一种蓄水单元,是一种典型的平原型水库,其与山谷型水库在功能上有许多类似之处. 但大型过水性湖泊与山谷型水库也有较多差别:1)山谷型水库一般是以坝址洪水作为水库防洪设计的依据,而大型过水性湖泊的洪水入流情况复杂,多是多条河流,多条通道,同时入湖,基本不存在坝址洪水这一概念;2)相比山谷型水库,大型过水性湖泊,特别是平原区的湖泊的水面面积较大,在湖区的降水基本不用汇流或者汇流时间很短,产流效果非常明显,对湖泊水位的影响极其显著,使得洪水更加难以控制;3)多数大型过水性湖泊的湖区范围内均存在着较多的蓄滞洪区,且部分蓄滞洪区的启用标准相对较低,通常需要采用水动力学方法模拟洪水在湖区的演进情况,而大多山谷型水库不存在该方面的需求[1-2].
设计洪水是水利工程防洪安全设计研究的主要内容[3]. 国内外学者对设计洪水的研究成果颇为丰富,主要包含以下多个方面:洪水抽样方法研究[4-5]、分布线型研究[6-7]、经验频率公式研究[8-9]、参数估计方法研究[10-11]、设计洪水过程线研究[12-13]、历史洪水和古洪水研究[14-15]、区域洪水频率分析[16-17]、可能最大降水与可能最大洪水研究[18-19]、分期设计洪水研究[20-22]、梯级水库设计洪水研究[23-24]等,经过多年的研究探索和实践应用,设计洪水目前已经形成了一套较为完整的理论体系. 近些年,随着Copula函数引入到水文领域中,使得该研究方向又出现了新的进展和热点问题,简单归纳为以下3个方面:1)Copula函数可以采用任意形式的边缘分布函数来推求联合分布函数,具有很强的灵活性和适应性,因此,使得考虑洪峰、洪量等多变量的设计洪水计算成为可能[25-26];2)虽然可以采用Copula函数建立多变量的联合分布,通过求解多变量组合情况的发生概率得到一定防洪标准下的多变量的设计值,但该法存在一个明显的问题,即:对于给定的重现期水平,存在无穷多种满足防洪标准的多变量组合,因此,如何科学合理地选择设计值是多变量设计洪水方法能否成功应用的关键[27-29];3)多变量设计洪水计算方法的核心是基于Copula函数构造多变量的联合分布函数,因此,在设计洪水的不确定分析方面,相比以往单变量设计洪水,多变量设计洪水计算方法还需要考虑Copula函数的不确定性及其两者不确定性的耦合技术[30-31].
目前,国内学者采用Copula函数推求多变量设计洪水的应用案例类型多为山谷型水库,从单一水库到梯级水库群均做了大量的研究工作,取得了多变量洪水联合分布构建方法、多变量洪水重现期的定义方式和多变量洪水设计值的选择准则等多方面的研究成果,证实了多变量联合分析比单变量分析能更全面地描述水文事件的内在规律,可以更好地满足防洪安全设计要求[32-34]. 但是针对大型过水性湖泊即平原型水库的应用研究却较为少见. 虽然大型过水性湖泊与山谷型水库有一些相似的水力特征[35-36],甚至山谷型水库的部分研究成果可以直接移用于湖泊的多变量洪水设计中,但是入湖洪水过程与入库洪水过程存在明显的差异. 因此,针对大型过水性湖泊入湖洪水特征,基于Copula函数对湖泊防洪安全设计研究是十分有必要的.
本文采用Copula函数构建多个联合分布函数,通过联合概率密度值度量多种洪水事件组合的相对可能性,并考虑总的入湖洪水过程与各分区入湖洪水过程的协调性,去探寻:1)在重现期已知的情况下,如何确定总的入湖洪量与洪峰的合理组成;2)在总的入湖洪量已知的情况下,如何确定各分区入湖洪量的分配方案. 最终提出一套基于总的入湖洪水过程推导各个分区入湖洪水过程的方法,为湖泊防洪安全设计应用提供理论基础,并拓展多变量分析技术在水利工程中的应用范围.
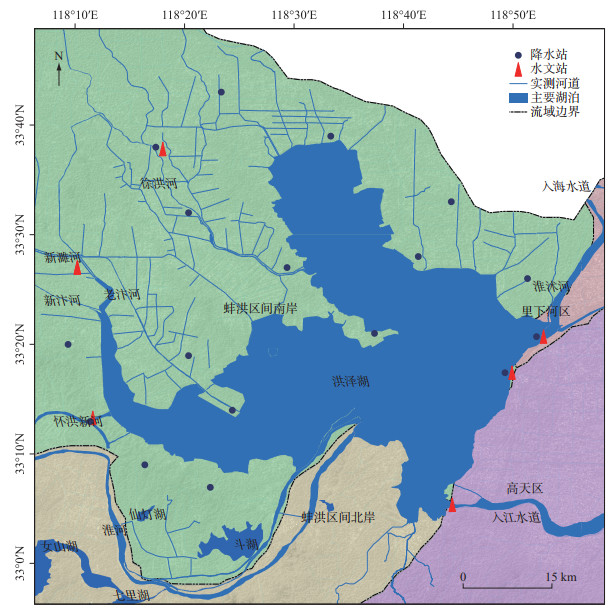
1 研究区与数据 1.1 流域概况洪泽湖位于江苏省境内,淮河流域中游末端,水域面积1597 km2,汛期控制水位12.5 m,正常蓄水位13.0 m,容积30.4×108 m3,是中国第4大淡水湖. 洪泽湖西纳淮河,南入长江,东贯黄海,北连沂沭水系,承接了淮河上中游豫、皖两省15.8×104 km2流域面积的来水,是淮河中游、支流与下游河道的联结点,长期以来,洪泽湖在淮河中下游防洪体系中发挥了重要的作用. 目前,洪泽湖主要的入湖河道有7条,除淮河干流外,还包含淮北区间的徐洪河、怀洪新河、老濉河、新濉河、新汴河以及淮南区间的池河,其中池河并不直接汇入洪泽湖,而是经女山湖汇入淮河干流后入湖,其余河道均直接汇入洪泽湖[37],洪泽湖地理位置及入湖河流和水文站点分布如图 1所示.
|
图 1 洪泽湖地理位置及入湖河流和水文站点分布 Fig.1 Location of the Lake Hongze and its rivers and gauging stations |
本文基于1960-2010年洪泽湖主要入湖河道的流量数据进行设计洪水分析,其中包括淮河干流(吴家渡站)、淮北区间的徐洪河(金锁镇站)、怀洪新河(峰山站)、老濉河(泗洪(老)站)、新濉河(泗洪(濉)站)、新汴河(团结闸站(闸下游))以及淮南区间的池河(明光站). 1960-2010年洪泽湖日入湖流量数据来自中华人民共和国水利部淮河水利委员会;1960-2010年各河道的洪峰数据来自淮河水利年鉴,部分河道缺失数据采用日流量代替.
2 方法 2.1 Copula函数的理论与基本方法Copula函数是定义在[0, 1]均匀分布的多维联合分布函数,根据Sklar理论[38],令H为一个n维分布函数,各变量的边缘分布为F1, F2, …, Fn,那么存在一个n-Copula函数C,使得对任意的x属于Rn,满足:
| $ H\left(x_{1}, x_{2}, \cdots, x_{n}\right)=C_{\theta}\left(F_{1}\left(x_{1}\right), F_{2}\left(x_{2}\right), \cdots, F_{n}\left(x_{n}\right)\right) $ | (1) |
| $ c_{\theta}\left(F_{1}\left(x_{1}\right), F_{2}\left(x_{2}\right), \cdots, F_{n}\left(x_{n}\right)\right)=\\\partial^{n} C_{\theta}\left(F_{1}\left(x_{1}\right), F_{2}\left(x_{2}\right), \cdots, F_{n}\left(x_{n}\right)\right) / \partial F_{1}\left(x_{1}\right) \partial F_{2}\left(x_{2}\right) \cdots \partial F_{n}\left(x_{n}\right) $ | (2) |
式中,θ为Copula函数的参数;若F1, F2, …, Fn是连续的,则函数C是唯一确定的;c为Copula函数C的密度函数.
对称Archimedean Copulas由于具有简单的函数构造,仅含一个参数,求解容易等特性,被广泛应用于水文多变量频率分析计算. 本文选取Archimedean Copulas中的Clayton Copula、Gumbel Copula、Frank Copula、Joe Copula这4种常用类型作为候选函数,采用最大似然法进行参数估计,利用赤池信息准则(AIC)、贝叶斯信息准则(BIC)、均方根误差(RMSE)对联合分布进行拟合优度检验. 本文选用的拟合优度检验公式为:
| $ A I C=2 k+n \ln \left(\frac{1}{n-1} \sum\limits_{i=1}^{n}\left(P_{e i}-P_{i}\right)^{2}\right) $ | (3) |
| $ B I C=\ln (n) k+n \ln \left(\frac{1}{n-1} \sum\limits_{i=1}^{n}\left(P_{e i}-P_{i}\right)^{2}\right) $ | (4) |
| $ R M S E=\frac{1}{n} \sqrt{\sum\limits_{i=1}^{n}\left(P_{e i}-P_{i}\right)^{2}} $ | (5) |
式中,Pei为联合经验频率,Pi为Copula函数联合分布值,k为模型中所含的参数,n为样本数. 检验值AIC、BIC、RMSE越小,表示Copula分布值Pi越靠近联合分经验概率值Pei,拟合精度越高.
2.2 入湖洪水的总峰和总量组合分析洪水事件作为一种随机水文事件,一般由洪峰与洪量等多个要素组成,各要素间通常存在着一定的相关关系. 设计洪水应当全面反映洪水事件的真实特征,尤其是针对大型过水性湖泊复杂的入流情况,更加需要通过多变量联合分析,并采用联合重现期来表征某一类洪水事件的发生频率,以达到同时考虑洪水各个要素之间的内在联系、更好地反映洪水事件特征的效果[39-40]. 在进行多变量洪水频率分析时,对于给定的联合重现期水平,存在满足防洪标准的无穷多种峰、量组合,但并非所有组合都符合水文事件的内在规律,只有在一定的范围内取值才是合理的. 因此,有必要确定峰量两变量联合重现期下入湖洪水总峰Qt和总量Wt组合的置信区间.
2.2.1 基于Copula函数推求总峰和总量联合分布假设Qt、Wt分别表示洪泽湖总入湖洪水的洪峰和洪量,对应的设计值分别为qt、wt,其边缘分布分别为FQt (qt)、FWt (wt),那么Qt和Wt的联合分布函数可用一个二维的Copula函数C表示.
| $ F\left(q_{t}, w_{t}\right)=C_{\theta}\left(F_{Q_{t}}\left(q_{t}\right), F_{W_{t}}\left(w_{t}\right)\right) $ | (6) |
式中,θ为Copula函数的参数;F(qt, wt)为Qt和Wt的联合分布函数.
2.2.2 总峰和总量的联合重现期在多变量联合重现期定义方法中“或”和“且”重现期(又称“OR”和“AND”重现期)是目前较为常用的重现期定义方法[41]. 基于Qt和Wt的联合分布函数,我们采用“或”的定义方法:当qt或wt中至少有一个被超过,那么即意味着设计值被破坏,该事件E(qt, wt)发生的重现期T(qt, wt)就等于防洪标准,具体公式表达为:
| $ P\left(q_{t}, w_{t}\right)=\{Q \geqslant q\} \cup\{W \geqslant w\} $ | (7) |
| $ T\left(q_{t}, w_{t}\right)=1 /\left(1-P\left(q_{t}, w_{t}\right)\right)=1 /\left(1-F\left(q_{t}, w_{t}\right)\right) $ | (8) |
式中,P(qt, wt)为事件E(qt, wt)的发生概率;T(qt, wt)为洪峰Qt和洪量Wt的联合重现期.
2.2.3 联合重现期下的总峰和总量置信区间估计在已知Qt和Wt联合分布函数为Cθ(FQt(qt), FWt(wt))的基础之上,假定联合重现期T为Z年一遇,那么洪量wt可以表示成为洪峰qt的函数,具体推导过程为:
| $ C_{\theta}\left(F_{Q_{t}}\left(q_{t}\right), F_{W_{t}}\left(w_{t}\right)\right)=1-1 / Z $ | (9) |
| $ F_{W_{t}}\left(w_{t}\right)=F\left(F_{Q_{t}}\left(q_{t}\right), 1-1 / Z\right) $ | (10) |
| $ w_{t}=F_{W_{t}}^{-1}\left(F\left(F_{Q_{t}}\left(q_{t}\right), 1-1 / Z\right)\right) $ | (11) |
式中,θ为Copula函数的参数;FWt-1为Wt的反函数.
因此,Qt和Wt联合分布函数的密度函数f(qt, wt)便可以转换为洪峰Qt的单值连续函数,我们便可绘制出在重现期为Z年的条件下,f(qt, wt)随Qt变化过程线,该过程线与横坐标轴所围成的面积为SQt,根据SQt,便可将f(qt, wt)进行归一化处理得到新的密度函数φq(qt). 具体推导过程为:
| $ f\left(q_{t}, w_{t}\right)=c\left(F_{Q_{t}}\left(q_{t}\right), F\left(F_{Q_{t}}\left(q_{t}\right), 1-1 / Z\right)\right) \cdot f_{Q_{t}}\left(q_{t}\right) \cdot f_{W_{t}}\left(F_{W_{t}}^{-1}\left(F\left(F_{Q_{t}}\left(q_{t}\right), 1-1 / Z\right)\right)\right) $ | (12) |
| $ S_{Q_{t}}=\int \limits_{0}^{+\infty} c\left(F_{Q_{t}}\left(q_{t}\right), F\left(F_{Q_{t}}\left(q_{t}\right), 1-1 / Z\right)\right) \cdot f_{Q_{t}}\left(q_{t}\right) \cdot f_{W_{t}}\left(F_{W_{t}}^{-1}\left(F\left(F_{Q_{t}}\left(q_{t}\right), 1-1 / Z\right)\right)\right) \mathrm{d} q_{t} $ | (13) |
| $ \varphi_{q}\left(q_{t}\right)=f\left(q_{t}, w_{t}\right) / S_{Q_{t}} $ | (14) |
式中,c为Cθ(FQt(qt), FWt(wt))的密度函数,f(qt)和f(wt)分别为Qt和Wt的密度函数.
根据φq(qt),选择合适的洪峰区间(qtdown, qtup使得
大型过水性湖泊的洪水入流情况复杂,多条河流,多条通道,同时入湖. 如果将每条河道的入流过程都单独考虑,这种做法不仅会忽略了河道之间天然的水文、水力联系,也会导致联合分布函数的维度过高,出现参数估计不准、分布拟合效果不佳,尾部相关性较强等问题[42]. 因此,本文采用皮尔森法(Pearson)、斯皮尔曼法(Spearman)计算各个河道之间的径流相关性,在考虑地理位置的基础上,将径流相关性较强的河道依次合并聚类,形成分区入湖径流.
2.4 入湖洪水总量的组成分析当整体入湖洪水的总量及分区数量确定时,存在无数种洪量的分区分配方案,但并非所有的洪量分配方案都符合水文事件的内在规律. 此外,有些洪量分区分配方案虽有可能出现,但其出现的概率却比较小,如在一场入湖洪水中,主要来水分区的洪量非常小,而次要来水分区的洪量却非常大. 因此,同样有必要确定分区洪量分配的置信区间,避免在分区洪水设计时,取到那些看似比较极端但实际上发生情况极小的分区洪量分配方案.
2.4.1 基于Copula函数推求各分区洪量的联合分布Wi表示各分区入湖洪水的洪量,对应的设计值分别为wi,其边缘分布函数分别为FWi(wi),那么分区间洪量Wi的联合分布函数表示为:
| $ F({w_1},{w_2}, \cdots ,{w_n}) = {C_\theta }({F_{{W_1}}}({w_1}),{F_{{W_2}}}({w_2}), \cdots ,{F_{{W_n}}}({w_n})) $ | (15) |
式中,θ为Copula函数的参数;F(w1, w2, …, wn)为分区间洪量Wi的联合分布函数;n为分区的个数.
2.4.2 洪水总量确定下分区洪量分配的置信区间估计在已知分区洪量联合分布函数为Cθ(FW1(w1), FW2(w2), …, FWn(wn))的基础之上,假定入湖总洪量为Wtotal,当分区数量n为2时,分区洪量w1和w2即存在着下列关系:w1+w2=Wtotal,因此,分区洪量w1和w2联合分布函数的密度函数f(w1,w2)便可以转换为分区洪量w1的单值连续函数f(w1,Wtotal-w1),在入湖总洪量为Wtotal的条件下,我们同样可以绘制出f(w1,w2)随w1变化的过程线,该过程线与横坐标轴所围成的面积为Sw1. 根据Sw1,便可将f(w1,w2)进行归一化处理得到新的密度函数φw(w1). 根据φw(w1),选择合适的洪量区间(w1down, w1up),使得
| $ f\left(w_{1}, w_{2}\right)=c\left(F_{W_{1}}\left(w_{1}\right), F\left(W_{\text {total }}-w_{1}, 1-1 / Z\right)\right) \cdot f_{W_{1}}\left(w_{1}\right) \cdot f_{W_{2}}\left(F_{W_{2}}^{-1}\left(F\left(W_{\text {total }}-w_{1}, 1-1 / Z\right)\right)\right) $ | (16) |
| $ S_{w_{1}}=\int \limits_{0}^{W_{\text {total }}} c\left(F_{W_{1}}\left(w_{1}\right), F\left(W_{\text {total }}-w_{1}, 1-1 / Z\right)\right) \cdot f_{W_{1}}\left(w_{1}\right) \cdot f_{W_{2}}\left(F_{W_{2}}^{-1}\left(F\left(W_{\text {total }}-w_{1}, 1-1 / Z\right)\right)\right) \mathrm{d} w_{1} $ | (17) |
| $ \varphi_{w}\left(w_{1}\right)=f\left(w_{1}, w_{2}\right) / S_{w_{1}} $ | (18) |
式中,c为Cθ(FW1(w1), FW2(w2))的密度函数,fW1(w1)和fW2(w2)分别为w1和w2的密度函数.
当分区数量n大于2时,分区洪量w1, w2, …, wn仍然存在着下列关系:
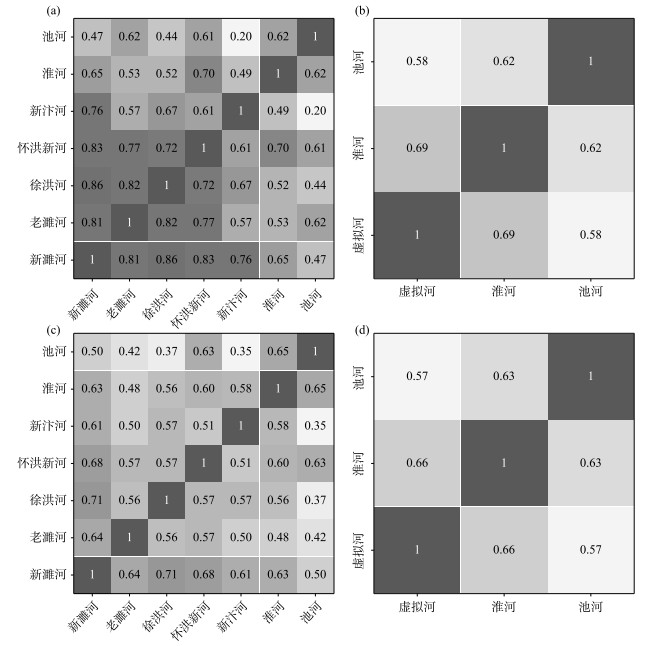
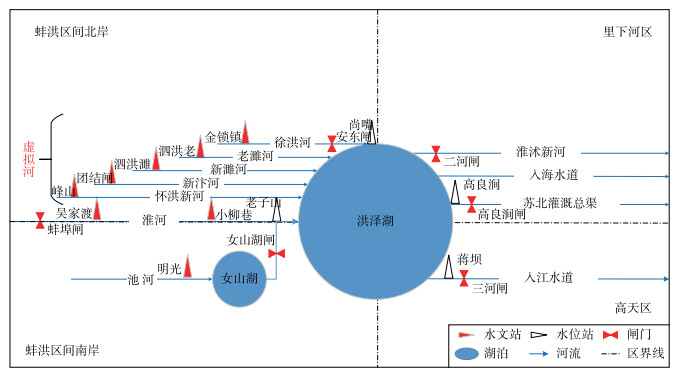
根据分析洪泽湖入湖的7条主要河道径流相关性可得到以下结论:新濉河、老濉河、徐洪河、怀洪新河、新汴河的径流相关性比较高,在Pearson和Spearman检验下多数能够达到0.70以上,属于强相关;池河与其他各条河道的径流相关性较差,在Pearson和Spearman检验下多数小于0.50,特别与新汴河的径流相关性只有0.20,属于弱相关;在Pearson和Spearman检验下,淮河与其余各河的径流相关性处于0.50~0.70之间(图 2a,c). 若将新濉河、老濉河、徐洪河、怀洪新河、新汴河的径流过程叠加形成一条虚拟河道,再次分析其与淮河、池河的径流相关性,发现河道间的径流相关性显著下降(图 2b,d). 因此,根据径流相关性分析,考虑地理拓扑关系和来水量的大小,在设计洪水时,将新濉河、老濉河、徐洪河、怀洪新河、新汴河合为一条虚拟河(该5条入湖河流的径流相关性强,均位于淮北区间,在水资源分区中同属蚌洪区间北岸,且各河道分别与淮河、池河的相关性和虚拟河与淮河、池河的相关性相近),分别与淮河、池河共同组成入湖洪水过程(图 3).
|
图 2 洪泽湖入湖河道的径流相关关系 Fig.2 The correlation results of runoff between rivers flowing into Lake Hongze |
|
图 3 洪泽湖与入湖洪水河流的拓扑关系 Fig.3 The topological relationship between Lake Hongze and flood rivers entering the lake |
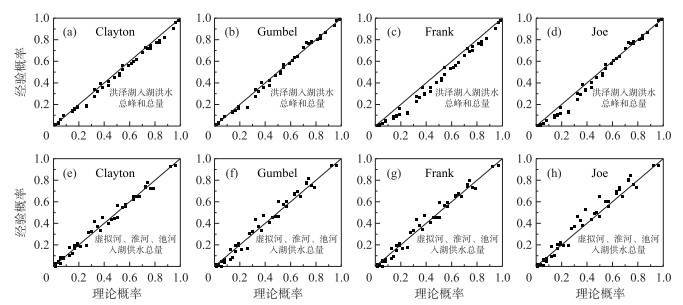
对于大型水库或者流域,Wt一般为30 d或者15 d洪量,对于小型水库或者流域,Wt一般为7 d或者3 d洪量. 洪泽湖总库容135亿m3,属于大(一)型水库,结合洪泽湖历史洪水特点,选择Wt为30 d的洪量(淮河流域防洪规划中对淮河干流100 a一遇洪水分别设计了30和60 d两套洪水方案,其中针对60 d洪水方案详细说明了洪泽湖对应的泄洪安排,此外由于洪泽湖具有较大的调洪作用,在设计洪水实践中多采用同频率法). 采用Copula函数构造上述多个联合分布,结果如表 1和图 4所示.
| 表 1 联合分布函数的拟合优度评价 Tab. 1 The goodness of fit tests for the joint distribution |
|
图 4 联合分布函数P-P图 Fig.4 The probability-probability plots of joint distribution function |
在选择洪泽湖入湖总峰qt和总量wt联合分布函数之前,采用Pearson、Spearman、Kendall秩次相关检验方法对qt和wt的相关关系进行检验,相应的秩相关系数分别为0.957、0.948、0.826,表明两变量之间是显著相关的. 观察表 1和图 4a~d,洪泽湖入湖洪水总峰qt和总量wt联合分布函数中,Gumbel Copula取得了最好的拟合效果,θ为5.32;观察表 1和图 4e~h,虚拟河、淮河、池河的洪水总量w1、w2、w3的联合分布函数中,Clayton Copula取得了最好的拟合效果,θ为2.39. 具体表达式如公式(19)、(20)所示.
| $ C\left(F_{Q_{t}}\left(q_{t}\right), F_{w_{t}}\left(w_{t}\right)\right)=\exp \left\{-\left[\left(-\ln F_{Q_{t}}\left(q_{t}\right)\right)^{5.32}+\left(-\ln F_{W_{t}}\left(w_{t}\right)\right)^{5.32}\right]^{1 / 5.32}\right\} $ | (19) |
| $ C\left(F_{W_{1}}\left(w_{1}\right), F_{W_{2}}\left(w_{2}\right), F_{W_{3}}\left(w_{3}\right)\right)=\left[F_{W_{1}}\left(w_{1}\right)^{-2.39}+F_{W_{2}}\left(w_{2}\right)^{-2.39}+F_{W_{3}}\left(w_{3}\right)^{-2.39}-2\right]^{-1 / 2.39} $ | (20) |
以洪泽湖入湖洪水总峰与总量联合重现期T=100 a为例,绘制等值线图,如图 5a所示. 绘制密度函数φq(qt)与总峰qt的关系曲线图,如图 5b所示. 选择置信水平α为0.05,根据图 5b,计算总峰与总量组合的上边界点(12225 m3/s,263亿m3)与下边界点(13025 m3/s,253亿m3).
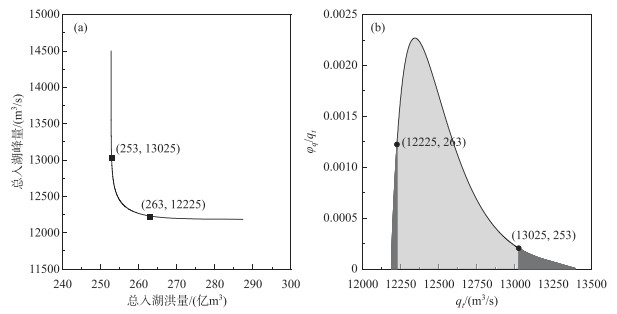
|
图 5 入湖洪水总峰与总量的95 % 置信区间 Fig.5 The 95 % confidence interval of the flood volume and flood peak of the whole flood process |
通过地区聚类分析可知洪泽湖入湖洪水的分区组成数量n大于2,因此,以洪泽湖30 d入湖洪量的变化范围的上、下边界点263亿和253亿m3为例,根据联合分布函数Cθ(FW1(w1), FW2(w2), FW3(w3)),分别生成1000000组地区洪量分配方案,绘制等值面图(图 6a,b). 选择置信水平α为0.05,确定等值面上95 % 置信区域的范围,并寻找各个分区洪量分配的最大值作为边界点. 在洪泽湖30 d入湖洪量为263亿m3时,确定的3个边界点值分别为:边界点1(83.88亿、172.98亿、6.14亿m3)、边界点2(2.40亿、260.42亿、0.18亿m3)、边界点3(34.96亿、203.88亿、24.16亿m3). 在洪泽湖30 d入湖洪量为253亿m3时,确定的3个边界点值分别为:边界点1(79.73亿、167.21亿、6.06亿m3)、边界点2(2.71亿、250.10亿、0.20亿m3)、边界点3(33.41亿、196.99亿、22.60亿m3). 最终在峰量联合重现期为百年一遇时,洪泽湖入湖洪水置信区间的分析结果如表 2所示.
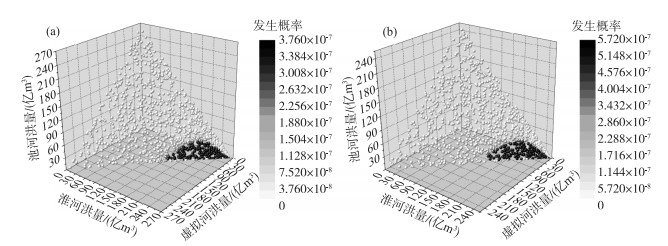
|
图 6 分区洪量分配的95 % 置信区间:(a) 洪量263亿m3;(b) 洪量253亿m3 (空间上的每一个球形点代表一套洪量分配方案,球形点的颜色代表该方案发生的概率) Fig.6 The 95 % confidence interval of flood volume allocation: (a) 263 million m3; (b) 253 million m3 |
| 表 2 联合重现期为百年一遇时入湖洪水置信区间分析结果 Tab. 2 The result of the confidence interval analysis with the joint return period is 100 years |
为验证该方法的合理性,选择淮河流域典型的洪水年份,并采用传统的洪水设计方法,设计重现期为100 a的洪泽湖入湖洪水过程,与本文的设计洪水结果进行对比分析. 1949-2019年期间,淮河流域发生过1954、1991、2003、2007年大水,后3次的大水均出现破圩、倒房的情况,给洪泽湖周边地区人民带来较大灾害. 因此本文选择1991、2003、2007年的洪水作为典型的洪水过程.
3.2.1 入湖洪水总峰与总量置信区间的合理性分析选用P-Ⅲ型曲线,通过线性矩法、目估视线法进行参数估计,拟合洪泽湖总入湖年最大洪峰和30 d洪量的频率分布. 根据拟合结果(表 3),将1991、2003、2007年所对应的典型洪水过程,采用“峰比”同倍比放大法推求洪泽湖总入湖设计洪水过程线(图 7a,c,e);采用“量比”同倍比放大法推求洪泽湖总入湖设计洪水过程线(图 7b,d,f).
| 表 3 洪泽湖总入湖设计洪水统计参数和设计值* Tab. 3 The result of design flood statistical parameters and values for Lake Hongze |
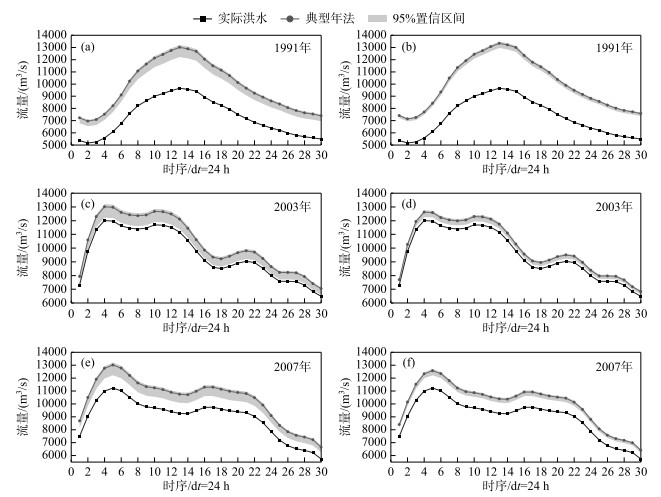
|
图 7 洪泽湖总入湖设计洪水过程线 Fig.7 The whole designed flood hydrograph of Lake Hongze |
由此得到以下3个结论:1)采用同倍比放大法推求的典型洪水过程均处于95 % 置信区间范围内,说明基于洪泽湖入湖洪水总峰和总量联合分布函数推求的设计洪水结果合理;2)“量比”放大法所得到的95 % 置信区间范围比“峰比”放大法所得到的95 % 置信区间范围窄,说明相比时段洪量,洪峰的随机性更为显著;3)采用同倍比放大法所得到的设计洪水过程均处于各自95 % 的置信区间范围的上部,说明采用单变量推求的洪水过程偏“安全”. 因此,在设计洪水过程中,有必要考虑洪水过程中各个特征量之间的相关性,使得设计洪水能够更加符合水文事件的内在规律.
3.2.2 地区聚类结果的合理性分析合理的地区聚类结果是分区洪量分配方案的基础,通过计算各入湖河道的年径流统计信息绘制箱线图,进一步分析聚类方法的合理性.
分析图 8可知,淮河是洪泽湖入湖洪水的主要来源,池河、怀洪新河、新汴河、新濉河、老濉河以及徐洪河为洪泽湖入湖洪水的次要来水区. 虽部分次要来水区(如老濉河、新汴河)的年径流量较小,但各次要来水区的年径流量之和在洪泽湖总入湖年径流量中所占比重较为可观,在设计入湖洪水中应当考虑. 淮河的年径流变化幅度最大,次要来水区的年径流变化范围较小,考虑到湖区洪水演进模拟需求,应当慎重将次要来水区与淮河合并,以免次要来水区的入流信息被掩盖. 次要来水区的年径流变化幅度较小,在设计洪水时可以根据实际需求适当合并简化分析,但合并时应考虑径流的相关关系以及地理位置信息,避免水系的割裂. 根据以上原则,本文地区聚类结果较为合理,主要原因如下:1)虚拟河是由怀洪新河、新汴河、新濉河、老濉河、徐洪河等淮北区间次要来水区聚类形成,其年径流统计信息与怀洪新河类似. 2)池河虽属于次要来水区,但由于其位于淮南区间,且与其他次要来水区的径流相关性较弱,所以单独成河. 3)淮河为主要来水区,与多数次要来水区的年径流相关性一般,如将邻近的次要来水区与其合并,必将次要来水区的径流信息掩盖,因此也单独成河. 此外,从图 8中淮河、池河、虚拟河的拟合分布曲线可以看出,淮河和虚拟河径流的不确定性相对较大,而池河的径流不确定性相对较小,与表 2的最终设计成果表现的趋势是一致的.
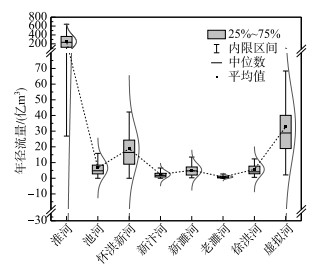
|
图 8 各入湖河道年径流量箱线图 Fig.8 The box-plot of annual runoff for each river |
选择1991、2003、2007年所对应的典型洪水过程,采用典型年法计算入湖总量为263亿m3时,虚拟河、淮河、池河所对应的30 d洪量,结果如图 9a所示;采用典型年法计算入湖总量为253亿m3时,虚拟河、淮河、池河所对应的30 d洪量,结果如图 9b所示.
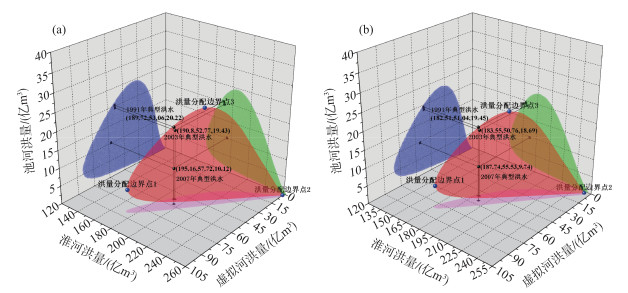
|
图 9 典型年法分区洪量分配方案:(a) 洪量263亿m3;(b) 洪量253亿m3 (红色区域为分区洪量分配方案的95 % 置信区间,黑色球形点代表采用典型年计算的洪量分配方案) Fig.9 The flood volume allocation schemes are computed by typical years method: (a) 263 million m3; (b) 253 million m3 |
由图 9a、b可知,入湖总量为263亿和253亿m3时,采用典型年法计算的分区洪量分配方案,均处于洪量分配的95 % 置信区域范围内,说明基于各地区洪量联合分布函数所推求的洪量分配95 % 置信区域具有合理性. 因此,在分区洪量分配过程中,有必要考虑各个分区洪量的相关性,使得洪量分配方案能够更加符合水文事件的内在联系.
根据本文的方法,在确定设计洪水的置信区间后,即可在此范围内对多变量进行联合选取,从而得到一系列多变量联合设计值. 在实际应用中,为避免取值的任意性和盲目性,可参考水库的研究成果[25, 42](如两变量同频率组合、条件期望组合),实现从置信区间落实到至最终的设计洪水方案. 此外,在研究的深化过程中,可进一步根据湖区洪水演进模拟的需求,针对聚类河道(如本文的虚拟河)采用“同频率”、“同倍比”、“典型年”等方法进行拆分,分别设计各条合并河道的洪水过程.
4 结论与展望针对大型过水性湖泊入湖洪水特征,本文基于Copula函数对通江连河湖泊的防洪安全设计进行研究,提出了一套从总入湖洪水过程,逐步推导至各分区入湖洪水过程的方法. 该方法首先根据入湖洪水的总峰和总量联合分布函数,推求在联合重现期下的总峰与总量95 % 的置信区间;通过径流相关性分析对入湖河道合并聚类,形成分区入湖径流,既考虑了河道间天然的水文、水力联系,也避免了联合分布函数维度过高的问题;之后根据分区洪水的洪量联合分布函数,推求在入湖洪水总量确定条件下分区洪量95 % 置信区域. 本文得到以下几个主要结论:
1) 在根据洪峰和洪量等两变量分析入湖洪水频率时,对于给定的联合重现期水平,存在满足防洪标准的无穷多种峰、量组合,但并非所有的组合都符合水文事件的内在规律,只有在一定范围内的取值才是合理的;
2) 大型过水性湖泊入湖洪水入湖情况复杂,通过径流相关性分析对入湖河道合并聚类,形成分区入湖过程,既能够考虑河道间天然的水文、水力联系,也可以避免联合分布函数维度过高的问题;
3) 在入湖总洪量已知的情况下,基于分区洪水的洪量联合分布函数,推求分区洪量95 % 置信区间的方法具有一定的合理性,其可以有效避免传统洪水地区分配方法的随机性和不确定性.
该套方法具有统计理论基础,结果合理可行,拓展了多变量洪水频率分析技术在水利工程实践中的应用范围,但也存在以下几个问题需在未来的研究中进行完善与改进:1)根据整体入湖洪水逐步推求各分区洪水的过程中,置信区间误差的传递和积累效应以及Copula函数的不确定性并未考虑;2)本文的实例中总入湖洪水仅分为3个分区,但在其他湖区的实际应用中可能会出现更多的分区数目,计算量级呈几何倍增大,应考虑改进方法以提高计算效率;3)对本文所提方法的合理性检验过程中,我们通过采用多种传统洪水设计方法进行对比验证,在未来的研究中还应将设计洪水结果输入相应的水文水动力学模型中进行洪水模拟与演算;4)在全球气候变暖的大背景下,流域层面上已经形成了较为复杂的气候-人类活动影响链,不同时期的洪水孕育环境发生了改变,使得水文序列产生了趋势性或跳跃性变异[44-45]. 而大型过水性湖泊的洪源众多,洪水地区组成复杂且地理气候条件不同,洪水特性各异. 因此,开展变化环境下非一致性水文设计值的研究对湖泊设计洪水具有独特的实践意义.
| [1] |
Hassanzadeh E, Zarghami M, Hassanzadeh Y. Determining the main factors in declining the Urmia Lake level by using system dynamics modeling. Water Resources Management, 2012, 26(1): 129-145. DOI:10.1007/s11269-011-9909-8 |
| [2] |
Li YL, Zhang Q, Yao J et al. Advances in integrated hydrological and hydrodynamic simulation of lake-catchment system. Resources and Environment in the Yangtze Basin, 2015, 24(2): 263-270. [李云良, 张奇, 姚静等. 湖泊流域系统水文水动力联合模拟研究进展综述. 长江流域资源与环境, 2015, 24(2): 263-270. DOI:10.11870/cjlyzyyhj201502012] |
| [3] |
Guo SL, Liu ZJ, Xiong LH. Advances and assessment on design flood estimation methods. Journal of Hydraulic Engineering, 2016, 47(3): 302-314. [郭生练, 刘章君, 熊立华. 设计洪水计算方法研究进展与评价. 水利学报, 2016, 47(3): 302-314.] |
| [4] |
Zhang LJ, Chen XH, Ye CQ et al. POT flood frequency analysis with historical floods in Wujiang River. Journal of Hydraulic Engineering, 2013, 44(3): 268-275. [张丽娟, 陈晓宏, 叶长青等. 考虑历史洪水的武江超定量洪水频率分析. 水利学报, 2013, 44(3): 268-275. DOI:10.3969/j.issn.0559-9350.2013.03.005] |
| [5] |
Dai CJ, Liang ZM, Luan CM et al. Advance in flood frequency analysis for partial duration series. Advances in Water Science, 2006, 17(1): 136-140. [戴昌军, 梁忠民, 栾承梅等. 洪水频率分析中PDS模型研究进展. 水科学进展, 2006, 17(1): 136-140. DOI:10.3321/j.issn:1001-6791.2006.01.022] |
| [6] |
Li SS. Study on the adaptability of several frequency distribution functions for China. Journal of China Hydrology, 1984, 4(1): 1-7. [李松仕. 几种频率分布线型对我国洪水资料适应性的研究. 水文, 1984, 4(1): 1-7.] |
| [7] |
Ye CQ, Chen XH, Shao QX et al. A comparison study on distribution for flood frequency analysis focus on the observed flow data in the high flow part. Journal of Hydraulic Engineering, 2013, 44(6): 694-702. [叶长青, 陈晓宏, 邵全喜等. 考虑高水影响的洪水频率分布线型对比研究. 水利学报, 2013, 44(6): 694-702.] |
| [8] |
Ji XW, Ding J, Shen HW et al. Plotting positions for Pearson type-Ⅲ distribution. Journal of Hydrology, 1984, 74(1/2): 1-29. DOI:10.1016/0022-1694(84)90137-9 |
| [9] |
Guo SL. Unbiased plotting position formulae for historical floods. Journal of Hydrology, 1990, 121(1/2/3/4): 45-61. DOI:10.1016/0022-1694(90)90224-L |
| [10] |
Greenwood JA, Landwehr JM, Matalas NC et al. Probability weighted moments: Definition and relation to parameters of several distributions expressable in inverse form. Water Resources Research, 1979, 15(5): 1049-1054. DOI:10.1029/WR015i005p01049 |
| [11] |
Liang ZM, Hu YM, Li BQ et al. A modified weighted function method for parameter estimation of Pearson type three distribution. Water Resources Research, 2014, 50(4): 3216-3228. DOI:10.1002/2013WR013653 |
| [12] |
Xiao Y, Guo SL, Liu P et al. Design flood hydrograph based on multicharacteristic synthesis index method. Journal of Hydrologic Engineering, 2009, 14(12): 1359-1364. DOI:10.1061/(asce)1084-0699(2009)14:12(1359) |
| [13] |
Chen YF. Comparison of the traditonal methods with the flood simulation method to calculate design flood control storage. Advances in Water Science, 2000, 11(1): 64-69. [陈元芳. 随机模拟法与传统方法推求设计防洪库容优劣的初步研究. 水科学进展, 2000, 11(1): 64-69. DOI:10.3321/j.issn:1001-6791.2000.01.012] |
| [14] |
Stedinger JR, Cohn TA. Flood frequency analysis with historical and paleoflood information. Water Resources Research, 1986, 22(5): 785-793. DOI:10.1029/WR022i005p00785 |
| [15] |
England JF Jr, Jarrett RD Jr, Salas JD Jr. Data-based comparisons of moments estimators using historical and paleoflood data. Journal of Hydrology, 2003, 278(1/2/3/4): 172-196. DOI:10.1016/S0022-1694(03)00141-0 |
| [16] |
Shu C, Ouarda TBMJ. Regional flood frequency analysis at ungauged sites using the adaptive neuro-fuzzy inference system. Journal of Hydrology, 2008, 349(1/2): 31-43. DOI:10.1016/j.jhydrol.2007.10.050 |
| [17] |
Yang T, Chen X, Yang HW et al. Regional flood frequency analysis in Pearl River Delta region based on L-moments approach. Journal of Hohai University: Natural Sciences, 2009, 37(6): 615-619. [杨涛, 陈喜, 杨红卫等. 基于线性矩法的珠江三角洲区域洪水频率分析. 河海大学学报: 自然科学版, 2009, 37(6): 615-619.] |
| [18] |
Wang GA. On flood prevention standard of reservoirs in China. Journal of Hydraulic Engineering, 2002, 33(12): 22-25. [王国安. 关于我国水库的防洪标准问题. 水利学报, 2002, 33(12): 22-25. DOI:10.3321/j.issn:0559-9350.2002.12.005] |
| [19] |
Wang GA. Comparison of the PMP/PMF estimating methods between USA and PRC. Hydrology, 2005, 25(5): 32-34. [王国安. 中美PMP/PMF估算方法基本框架比较. 水文, 2005, 25(5): 32-34. DOI:10.3969/j.issn.1000-0852.2005.05.008] |
| [20] |
Singh VP, Wang SX, Zhang L. Frequency analysis of nonidentically distributed hydrologic flood data. Journal of Hydrology, 2005, 307(1/2/3/4): 175-195. DOI:10.1016/j.jhydrol.2004.10.029 |
| [21] |
Cunderlik JM, Ouarda TBMJ, Bobée B. On the objective identification of flood seasons. Water Resources Research, 2004, 40(1): W01520. DOI:10.1029/2003WR002295 |
| [22] |
Feng P, Xu XG, Li H. Method to divide flood season based on the fuzzy set analysis and its application. Resources and Environment in the Yangtze Basin, 2008, 17(3): 495-499. [冯平, 徐向广, 李海. 基于模糊集合分析的汛期分期方法及其应用. 长江流域资源与环境, 2008, 17(3): 495-499. DOI:10.3969/j.issn.1004-8227.2008.03.032] |
| [23] |
Lu BH, Gu HH, Xie ZY et al. Stochastic simulation for determining the design flood of cascade reservoir systems. Hydrology Research, 2012, 43(1/2): 54-63. DOI:10.2166/nh.2011.002 |
| [24] |
Li TY, Guo SL, Liu ZJ et al. Design flood estimation methods for cascade reservoirs. Journal of Hydraulic Engineering, 2014, 45(6): 641-648. [李天元, 郭生练, 刘章君等. 梯级水库下游设计洪水计算方法研究. 水利学报, 2014, 45(6): 641-648.] |
| [25] |
Li TY, Guo SL, Liu ZJ et al. Design flood estimation based on bivariate joint distribution of flood peak and volume. Journal of Hydraulic Engineering, 2014, 45(3): 269-276. [李天元, 郭生练, 刘章君等. 基于峰量联合分布推求设计洪水. 水利学报, 2014, 45(3): 269-276.] |
| [26] |
Feng P, Mao HH, Wang Y. Method for hydrological reoccurrence frequency analysis under the condition of multivariate. Journal of Hydraulic Engineering, 2009, 40(1): 33-37. [冯平, 毛慧慧, 王勇. 多变量情况下的水文频率分析方法及其应用. 水利学报, 2009, 40(1): 33-37. DOI:10.3321/j.issn:0559-9350.2009.01.005] |
| [27] |
Volpi E, Fiori A. Design event selection in bivariate hydrological frequency analysis. Hydrological Sciences Journal, 2012, 57(8): 1506-1515. DOI:10.1080/02626667.2012.726357 |
| [28] |
Gräler B, van den Berg MJ, Vandenberghe S et al. Multivariate return periods in hydrology: A critical and practical review focusing on synthetic design hydrograph estimation. Hydrology and Earth System Sciences, 2013, 17(4): 1281-1296. DOI:10.5194/hess-17-1281-2013 |
| [29] |
Requena AI, Mediero L, Garrote L. A bivariate return period based on Copulas for hydrologic dam design: Accounting for reservoir routing in risk estimation. Hydrology and Earth System Sciences, 2013, 17(8): 3023-3038. DOI:10.5194/hess-17-3023-2013 |
| [30] |
Serinaldi F. An uncertain journey around the tails of multivariate hydrological distributions. Water Resources Research, 2013, 49(10): 6527-6547. DOI:10.1002/wrcr.20531 |
| [31] |
Dung NV, Merz B, Bárdossy A et al. Handling uncertainty in bivariate quantile estimation-An application to flood hazard analysis in the Mekong Delta. Journal of Hydrology, 2015, 527: 704-717. DOI:10.1016/j.jhydrol.2015.05.033 |
| [32] |
Xiong LH, Guo SL, Xiao Y et al. Application of Copulas to multivariate hydrological frequency analysis. Engineering Journal of Wuhan University, 2005, 38(6): 16-19. [熊立华, 郭生练, 肖义等. Copula联结函数在多变量水文频率分析中的应用. 武汉大学学报: 工学版, 2005, 38(6): 16-19.] |
| [33] |
Salvadori G, de Michele C. On the use of Copulas in hydrology: Theory and practice. Journal of Hydrologic Engineering, 2007, 12(4): 369-380. DOI:10.1061/(asce)1084-0699(2007)12:4(369) |
| [34] |
Zhang L, Singh VP. Trivariate flood frequency analysis using the gumbel-hougaard Copula. Journal of Hydrologic Engineering, 2007, 12(4): 431-439. DOI:10.1061/(asce)1084-0699(2007)12:4(431) |
| [35] |
Liu HM. Research and application on estimation methods of design flood region composition[Dissertation]. Wuhan: Wuhan University, 2005. [刘画眉. 设计洪水地区组成计算方法研究及应用[学位论文]. 武汉: 武汉大学, 2005. ]
|
| [36] |
Huang Y, Ding ZL, Guo HJ et al. Design flood calculation of Poyang Lake based on concept of total inflow. Yangtze River, 2015, 46(1): 58-60. [黄燕, 丁志立, 郭海晋等. 基于总入流概念的鄱阳湖设计洪水计算. 人民长江, 2015, 46(1): 58-60.] |
| [37] |
Wang Q, Chen JY. Formation and evolution of Hongze Lake and the Huaihe River mouth along the lake. J Lake Sci, 1999, 11(3): 237-244. [王庆, 陈吉余. 洪泽湖和淮河入洪泽湖河口的形成与演化. 湖泊科学, 1999, 11(3): 237-244. DOI:10.18307/1999.0308] |
| [38] |
Sklar A. Random variables, distribution functions, and Copulas-a personal look backward and forward. Institute of Mathematical Statistics Lecture Notes-Monograph Series. Hayward, CA: Institute of Mathematical Statistics, 1996: 1-14. DOI:10.1214/lnms/1215452606
|
| [39] |
de Michele C, Salvadori G, Canossi M et al. Bivariate statistical approach to check adequacy of dam spillway. Journal of Hydrologic Engineering, 2005, 10(1): 50-57. DOI:10.1061/(asce)1084-0699(2005)10:1(50) |
| [40] |
Guo SL, Yan BW, Xiao Y et al. Multivariate hydrological analysis and estimation. Journal of China Hydrology, 2008, 28(3): 1-7. [郭生练, 闫宝伟, 肖义等. Copula函数在多变量水文分析计算中的应用及研究进展. 水文, 2008, 28(3): 1-7.] |
| [41] |
Salvadori G, de Michele C, Durante F. On the return period and design in a multivariate framework. Hydrology and Earth System Sciences, 2011, 15(11): 3293-3305. DOI:10.5194/hess-15-3293-2011 |
| [42] |
Luo Y, Dong ZC, Guan XK et al. Flood risk analysis in the Taihu Basin during flood periods based on Copula function. J Lake Sci, 2020, 32(1): 223-235. [罗赟, 董增川, 管西柯等. 基于Copula函数的太湖流域汛期洪涝灾害危险性分析. 湖泊科学, 2020, 32(1): 223-235. DOI:10.18307/2020.0121] |
| [43] |
Li TY, Guo SL, Chen L et al. Safety design for reservoir flood control based on Copula function. Journal of Hydroelectric Engineering, 2013, 32(6): 50-56. [李天元, 郭生练, 陈璐等. 基于Copula函数的水库防洪安全设计. 水力发电学报, 2013, 32(6): 50-56.] |
| [44] |
Jiang C, Xiong LH, Yan L et al. Multivariate hydrologic design methods under nonstationary conditions and application to engineering practice. Hydrology and Earth System Sciences, 2019, 23(3): 1683-1704. DOI:10.5194/hess-23-1683-2019 |
| [45] |
Hu YM, Liang ZM, Yao Y et al. Review on computational methods of hydrological design values in changing environment. Advances in Science and Technology of Water Resources, 2018, 38(4): 89-94. [胡义明, 梁忠民, 姚轶等. 变化环境下水文设计值计算方法研究综述. 水利水电科技进展, 2018, 38(4): 89-94.] |
 2021, Vol. 33
2021, Vol. 33 


