(2: 中国科学院重庆绿色智能技术研究院, 大数据与智能计算重庆市重点实验室, 重庆 400714)
(2: Chongqing Institute of Green and Intelligent Technology, Chinese Academy of Sciences, Chongqing Key Laboratory of Big Data and Intelligent Computing, Chongqing 400714, P. R. China)
筑坝拦截会改变河流的水文情势,从水动力条件、水下光热结构、养分来源及其输送强度等方面,形成微观生境的时空异质性,加之大量陆源营养物受淹溶出,极易诱发藻类大量繁殖形成水华现象[1-2]. 近年来,全世界大型河流中有害水华事件的数量和规模都不断增加[3]. 因而,需要研发水华的早期监测预警系统,帮助水资源管理人员快速诊断藻类变化,减少水华发生的风险和治理成本. 但是,水华暴发是一个复杂的生态事件,是由特定水体中物理、化学和生物因素相互耦合作用引起的,变量间往往呈现出高维非线性的映射关系[4-5],需要借助于模型工具来实现生态系统变化的全面评估. 目前,预测藻类动态变化主要有两种建模策略:机理过程模型和机器学习算法. 其中基于生态动力学过程的方法是模拟和分析藻类动态变化最有效的技术,并在水生态系统长期演替趋势分析中取得广泛的应用. 但水华暴发涉及的生态过程还尚存着机理不明晰,或难以用数学来表达的问题[5]. 随着大数据时代的到来和人工智能技术的迅猛发展,数据驱动的建模方式逐渐在水华短期预测上得到重视[6].
特别是人工神经网络被广泛应用在藻类动态变化预测上,如BP神经网络(back propagation neural network, BPNN)[7]、径向基(radial basis function,RBF)神经网络[8]、小波神经网络(wavelet neural network,WNN)[9]和深度置信网络(deep belief network,DBN)[10]. 但是,上述方法并未对时间序列数据开发,对单批次输入时间序列数据前后之间的依赖关系缺乏考虑. 而长短期记忆神经网络(long short-term memory neural network, LSTM-NN)作为一种时间递归神经网络,在保留传统循环网络(recurrent neural network,RNN)对连续时间序列处理能力的同时,可有效地解决时间依赖上的问题,已经在自然语言处理领域取得了巨大的成功,国内外最新研究也尝试将LSTM引用于藻类动态预测上. 如Yu等[11]将小波分析和LSTM相结合提出了WDTD-LSTM-WMF长期预测模型,并结合地理空间分析模拟了滇池叶绿素a浓度的历史变化过程,并有效地预测了叶绿素a浓度的未来变化趋势;Wang等[12]利用福建海洋预报站2009-2011年的监测数据,构建了预测叶绿素a浓度的LSTM时空分布模型,结果表明该模型能够很好地处理水质指标与叶绿素a浓度之间的非线性关系;Lee等[13]将3种深度学习模型(多层感知器MLP、RNN和LSTM)和普通最小二乘OLS回归分析方法用于韩国4条主要河流的水华预测并进行比较分析,LSTM模型在其中表现出最优的性能;Shin等[14]利用LSTM模型,基于卫星收集到的海表温度和光合有效辐射数据对韩国南海赤潮发生进行预测.
然而,LSTM模型的预测效果依赖于输入变量的可靠性,当使用离散监测数据评估藻类动态变化时,模型预测性能可能会受到一定限制,但尚未有研究探索藻类在线监测数据与LSTM结合的问题;此外,考虑到藻类在线监测数据会受各种随机因素的影响,呈现出非稳态的时序变化特征,会影响模型训练与预测的稳定性,因而有必要对获取的信息提取进行降噪处理. 小波变换(wavelet transformation,WT)具有良好的时频分辨功能,是分析生态时间序列中经常出现的非平稳、非周期性和含噪声信号的有力工具[15]. 例如在用神经网络对北京河湖进行水华预测的研究结果表明,经过小波分析降噪处理后的数据能有效避免其中噪声部分对网络的干扰,提高网络的性能[16]. 为此,本研究以在线系统获取的监测数据为基础,构建基于小波变换和LSTM网络的藻类时序预测模型,探讨模型在三峡水库4条支流叶绿素a时序变化预测上的表现,以期为水华的监测预警系统构建提供借鉴与依据.
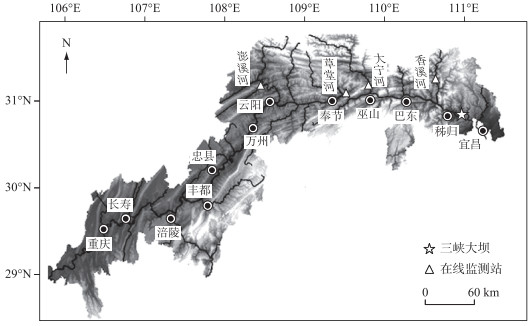
1 材料与方法 1.1 研究区域概况三峡大坝自2003年建成蓄水后,部分支流受干流回水顶托的影响,表现出区别经典河湖的水动力学特征,极易诱发藻类大量繁殖而形成水华[17-18]. 本研究围绕三峡库区4条支流香溪河、澎溪河、大宁河及草堂河开展,具体位置如图 1所示. 香溪河(31°04′~31°34′N,110°25′~111°06′E)全长94 km,是三峡库区中距离大坝最近的支流,与大坝相距仅34.5 km,形成了长约40 km的回水区. 位于三峡库区中部的草堂河(30°35′~31°26′N,108°14′~109°25′E),距大坝165 km,全长31.4 km,有约8 km的回水区. 处于三峡库区中上部的大宁河(31°04′~31°44′N,108°44′~110°11′E)长162 km,最大深度110 m,位于大坝上游123 km处,回水区约60 km. 彭溪河(31°00′~31°42′N,107°56′~108°54′E)处于三峡库区的中段,是库区北岸流域面积最大的支流全长182 km,位于大坝上游约250 km的地方,回水区约60 km.
|
图 1 三峡库区支流监测点位分布示意 Fig.1 Distribution of monitoring sites in tributaries of the Three Gorges Reservoir |
基于研究团队在4条河流分别安置的以浮标为载体的在线监测系统,选取多参数水质分析仪(型号AP7000,Aquaread)获取的叶绿素a浓度来指示藻类动态变化. 监测数据以10 min/次的频率原位采集,并通过CDMA2000(中国电信)网络实时传输到控制中心. 考虑到计算成本与管理需求,将叶绿素a原始值求每小时平均后作为模型输入,本研究提取出一个完整水文年的数据对模型进行训练与测试(2017年9月1日至2018年8月31日,总计35040条). 为保障监测数据可靠性,仪器每两周进行维护与校验,确保数据集中缺失与离异值占比较低(<1 %).
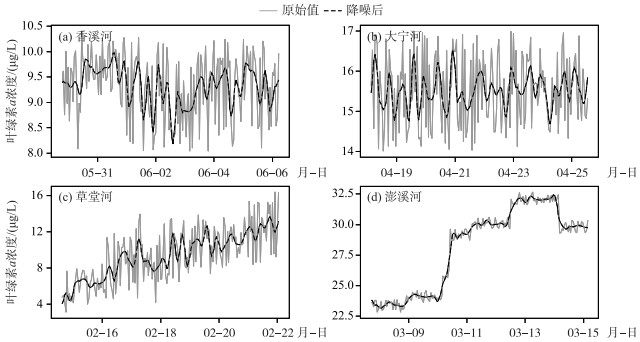
1.2.2 小波变换预处理由于受到各种不确定因素的干扰,在线数据时序变化特征常表现为非平稳趋势(non-stationary),直接输入模型后会影响到预测精度. 叶绿素a浓度作为表征水华的一个重要参数,在实际测定叶绿素a浓度的过程中,往往会受天气(雨、雪等)、引水过程和仪器精度等随机因素的影响,使测量值含有噪声,噪声的存在会淹没叶绿素序列的真实变化规律[16]. 因此,本文采用小波变换方法对原始数据进行预处理,包括小波分解与小波重构2个主要过程. 小波分解可获得多个层次的分解结果,每一层的结果都是将原低频信号分解成低频和高频2个部分,在经过n层分解之后源信号被分解为一个低频信号(An)以及若干高频信号(D1, D2, …,Dn),源信号数据的噪声一般集中在高频信号部分,可对高频部分进行一定处理,然后与低频部分进行小波重构,还原成降噪数据[19]. 为使LSTM模型更有效地提取隐藏的信息,本研究选取应用较广的Daubechies小波族中的db4小波函数将叶绿素a浓度时序数据经3层分解得到的高频信息滤除,仅保留低频数据以刻画叶绿素a浓度的变化趋势,其中部分数据降噪处理前后的结果对比如图 2所示,从图中可以看出经过小波变换降噪后的叶绿素时序信号较为平滑,同时也很好地保留了叶绿素的动态变化.
|
图 2 小波变换降噪前后数据对比 Fig.2 Data comparison before and after wavelet transform noise reduction |
为利于模型抽提出更多的特征,本文对叶绿素a时序数据按照式(1)进行极差标准化处理,使样本数据处于[0, 1]区间内.
| $ \hat X = \frac{{X - {X_{\min }}}}{{{X_{\max }} - {X_{\min }}}} $ | (1) |
式中,X和
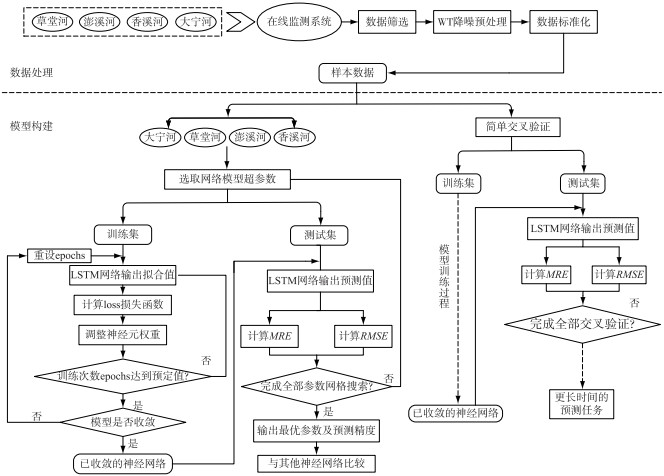
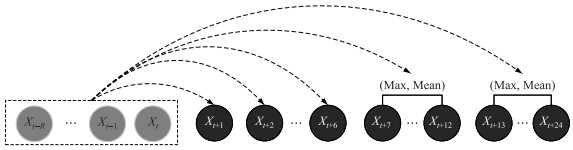
LSTM模型采用主流的TensorFlow深度学习框架实现,具体的技术路线如图 3所示. 数据经预处理和标准化后,采用3个步骤研究LSTM对叶绿素a的预测效果. 首先,将不同河流于2017年9月1日至2018年5月31日采集的叶绿素a数据(占总样本的75 %)作为训练集,2018年6月1日至8月31日的叶绿素a数据(占总样本的25 %)作为测试集,分别构建每条支流的水华预测模型;随后,为进一步验证LSTM模型的泛化能力,在样本数据扩大的情况下对模型进行校验,选取任一条河流的样本数据为测试集,其余3条河流的样本数据为训练集,对叶绿素a的预测进行交叉验证;最后,为衡量不同时间尺度下模型对叶绿素a预测效果的影响,分别在1~24 h范围内设置不同时间尺度,对叶绿素a预测效果进行比较. 如图 4所示,在1~6 h内的短期预测上,模型预测目标是以小时为节点递增的叶绿素a浓度;在相对长的时间尺度上,采用7~12和13~24 h两个区段内叶绿素a浓度极大值与均值,以评价模型在不同时间步长下对叶绿素a浓度的预测效果. 这是考虑到特定时间区间内叶绿素a浓度的峰值表征水华的严重程度,而其均值则反映出时序变化的整体趋势.
|
图 3 基于WT-LSTM神经网络的水华预测模型流程 Fig.3 Process of water bloom prediction model based on WT-LSTM neural network |
|
图 4 不同时间尺度下的预测形式 Fig.4 Prediction forms at different time scales |
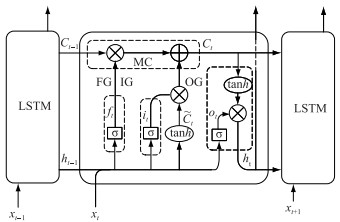
LSTM最早是由Hochreiter和Schmidhuber所提出,为了解决传统RNN不能捕捉输入序列中的长时间依赖关系,而产生梯度消失和梯度爆炸的问题[20]. LSTM核心在于有一个用来储存信息状态的记忆单元(memory cell,MC),并通过3个门控单元(输入门、输出门和遗忘门)的结构来调节进出记忆单元的信息流(图 5). 记忆单元可保留时序中的隐藏信息,以便LSTM利用较长时间序列的信息;3个门控单元则通过sigmoid函数的激活与否来改变记忆单元中的信息状态,其中遗忘门(forget gate,FG)用来决定从记忆单元状态中丢弃哪些信息,而输入门(input gate,IG)用于确定向记忆单元状态中添加那些新信息,最后输出门(output gate,OG)控制输出当前单元状态的信息.
|
图 5 LSTM神经网络在时序上的展开 Fig.5 Expansion of LSTM neural network in time series |
LSTM模型涉及到主要参数包括神经网络层数、每层神经元节点数及回溯时间步长数. 在网络结构设计中,通过预先多次的比较实验,并考虑到模型的复杂度与计算效率,确定相关参数取值集合的范围:神经网络层数取值{1,2,3};每层隐藏神经元个数取值{40,80,120,160};回溯时间步长取值{6,12,24}. 本文从结构参数集中随机选取一组值来构建模型,并采用5倍K折叠交叉验证的随机搜索方法,将数据集等比例划分为K份,选择其中1份作为测试,其余K-1份数据用于训练,保证每个部分的数据都做过测试,每次实验得到K个模型并综合评价,比较不同参数取值对于模型性能的影响,最终得到最优的参数组合.
1.3.3 模型训练过程LSTM训练过程中采用随时间反向传播(back propagation through time, BPTT)算法,主要分为3步.
① 向前计算每个神经元的输出值. 在计算中的信息流动方向在图 5中用箭头标明,具体的计算过程可以用下列公式来表示:
| $ {f_t} = \sigma \left( {{W_{\rm{f}}} \cdot \left[ {{h_{t - 1}}, {x_t}} \right] + {b_{\rm{f}}}} \right) $ | (2) |
| $ {i_t} = \sigma \left( {{W_{\rm{i}}} \cdot \left[ {{h_{t - 1}}, {x_t}} \right] + {b_{\rm{i}}}} \right) $ | (3) |
| $ {C_t} = {f_t}*{C_{t - 1}} + {i_{\rm{t}}}*\tanh \left( {{W_{\rm{C}}} \cdot \left[ {{h_{t - 1}}, {x_t}} \right] + {b_{\rm{C}}}} \right) $ | (4) |
| $ {o_t} = \sigma \left( {{W_{\rm{o}}}*\left[ {{h_{t - 1}}, {x_t}} \right] + {b_{\rm{o}}}} \right) $ | (5) |
| $ {h_t} = {o_t} \cdot \tanh \left( {{C_t}} \right) $ | (6) |
式中,ft、it和ot分别表示遗忘门、输入门和输出门的激活函数;Ct-1和Ct分别表示记忆单元中前一时刻和现在时刻的状态向量;ht-1和ht分别表示LSTM的隐藏层前一时刻和现在时刻的输出向量;xt表示当前的输入向量;W和b分别表示各单元结构的权重矩阵和偏差向量;"*"表示矩阵逐元素点乘. 另外,σ(·)表示Sigmoid函数,tanh(·)表示双曲正切函数,其计算公式分别为:
| $ \sigma (x) = \frac{1}{{1 + {{\rm{e}}^{ - x}}}} $ | (7) |
| $ \tanh (x) = \frac{{{{\rm{e}}^x} - {{\rm{e}}^{ - x}}}}{{{{\rm{e}}^x} + {{\rm{e}}^{ - x}}}} $ | (8) |
② 反向计算每个神经元的误差项,并根据误差项计算权重梯度. 本文的目标是预测未来河流中叶绿素a浓度变化,故选取均方误差(mean square error, MSE)作为损失函数,其中每个训练样本的平方误差损失是实际值和预测值之差的平方,模型平均损失函数L定义如下:
| $ L(\theta ) = \frac{1}{{2m}}\sum\limits_{i = 1}^m {{{\left( {{y^i} - {f_\theta }\left( {{x^i}} \right)} \right)}^2}} $ | (9) |
式中, 单个样本的损失为网络的输出值fθ(xi)和目标输出值yi的平方差,m表示样本的数目,θ为模型学习的权重参数. 对于长度为n的样本序列,输出值fθ(x)的表达式为:
| $ {f_\theta }(x) = {\theta _1}{x_1} + {\theta _2}{x_2} + \cdots + {\theta _n}{x_n}, j \in \{ 1, 2 \cdots n\} $ | (10) |
在梯度下降算法中,需要先对参数求导,得到梯度. 将每个样本中某一参数θj求导后求和得到式(11):
| $ \frac{\partial }{{\partial {\theta _j}}}L(\theta ) = \frac{1}{m}\sum\limits_{i = 1}^m {\left( {{y^i} - {f_\theta }\left( {{x^i}} \right)} \right)} x_j^i $ | (11) |
③ 应用梯度下降算法更新权重. 本文模型在训练过程中的算法选取由Kingma和Ba所提的出适应性动量估计(adaptive moment estimation, Adam)算法,与其他优化算法相比,Adam算法计算更为高效、实际应用中效果更好[21]. Adam算法作为经典随机梯度下降算法的拓展,能更加有效地更新网络权重,在应用过程中使用动量与自适应学习率来加快网络的收敛速度,使得模型沿梯度的负方向更新参数,同时为了避免模型在学习过程中容易遇到的过拟合问题,本文通过采用L2正则化方法可以使模型多次迭代所得到的权重参数θj不断减小,而参数较小的模型泛化能力也更强,在一定程度上避免了过拟合现象,因为当权重值很大时,数据偏移一点对结果都会造成很大的影响. 最终得到用于迭代计算权重参数θj的公式(12):
| $ {\theta _j} = {\theta _j}\left( {1 - \alpha \frac{\lambda }{m}} \right) - \alpha \frac{1}{m}\sum\limits_{i = 1}^m {\left( {{y^i} - {f_\theta }\left( {{x^i}} \right)} \right)} x_j^i $ | (12) |
评价模型的性能采用均方根误差(root mean square error,RMSE)、平均相对误差(mean relative error,MRE)和纳什效率系数(Nash efficiency coefficient,NSE). 计算所得的RMSE和MRE的值越小,NSE值越接近1,则模型预测的精度越高可信度也越高,具体公式如下:
| $ {RMSE = \sqrt {\frac{1}{n}\sum\limits_{t = 1}^n {{{\left( {{y_t} - y_t^*} \right)}^2}} } } $ | (13) |
| $ {MRE = \frac{1}{n}\sum\limits_{t = 1}^n {\left| {\frac{{{y_t} - y_t^*}}{{y_t^*}}} \right|} \times 100\% } $ | (14) |
| $ {NSE = 1 - \frac{{\sum\limits_{t = 1}^n {{{\left( {{y_t} - y_t^*} \right)}^2}} }}{{\sum\limits_{t = 1}^n {{{\left( {y_t^* - \hat y_t^*} \right)}^2}} }}} $ | (15) |
式中,n为样本数,yt*、
利用小波变换(WT)与长短期记忆网络(LSTM)构建藻类时序变化预测模型,分别对4条支流叶绿素a浓度进行学习与预测. 表 1为利用随机网格搜索获取的最优参数组合,以香溪河为例,WT-LSTM模型对水华预测最好的参数组合为:神经网络层数取2、每层隐藏神经元取120、回溯时间步长取24 h. 考虑到模型需反复不断地调整网络结构和参数,以获得具有误差较低、训练时间短及精度较高的最佳参数组合[22],因此,4条支流预测模型所选择的参数并不一致,体现香溪河和草堂河相较大宁河和澎溪河在网络层数、神经元数等参数取值上更大,也证实前两者所构建的神经网络相对更加复杂.
| 表 1 WT-LSTM神经网络在4条河流中的最优参数组合 Tab. 1 Optimal parameter combination of WT-LSTM neural network in four rivers |
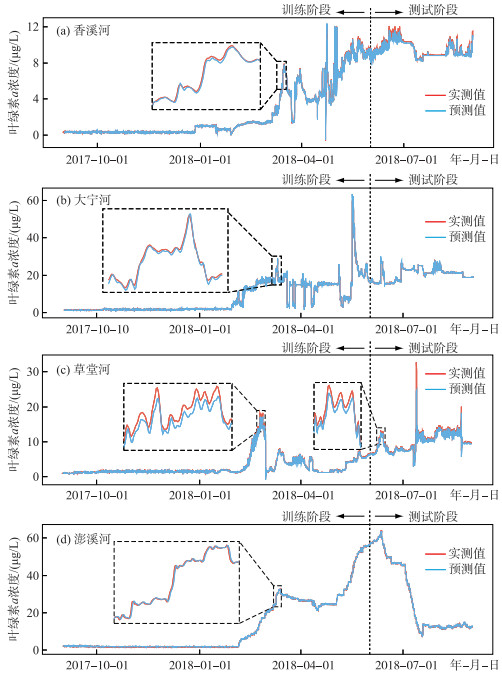
在最优参数组合下,图 6给出WT-LSTM模型对叶绿素a浓度的预测效果(1 h预测为例). 结果表明在不同河流数据集的应用中,WT-LSTM模型在训练和测试阶段均表现出较好的预测效果,NSE值均接近1,具体在澎溪河、草堂河、大宁河和香溪河依次为0.999、0.993、0.997和0.996,表明WT-LSTM模型可学习到在线数据的潜在变化趋势. 为进一步验证WT-LSTM模型的泛化能力,在样本数据扩大的情况下对模型进行校验,首先分析了4条河流中叶绿素a浓度的空间相关性,结果如表 2所示,河流中叶绿素a浓度间均显著相关(P<0.01),证明这4条河流叶绿素a浓度变化趋势具有一定的相似性;然后选取3条河流叶绿素a数据训练模型,另一条河流的叶绿素a浓度测试模型,模型预测效果如表 3所示. 可以观察到WT-LSTM模型对4条河流叶绿素a浓度值皆有较好的预测效果,无论选取4条河流中任意一条河流作为测试集,所得到的预测结果与实际监测值之间吻合程度较高,平均相对误差均不超过5 %,具体在澎溪河、草堂河、大宁河和香溪河依次为1.36 %、1.70 %、2.51 % 和4.74 %;不同数据集的交叉验证实验表明,模型可耦合多个监测站点数据,扩大训练与测试样本空间,提供模型的泛化能力. 因而,在湖库中在线监测系统应用上,可以学习多个具备相似特征的在线监测数据,提高模型对具体问题的预测能力.
|
图 6 WT-LSTM模型监测期间内在4条河流中叶绿素a浓度预测值和实测值对比 Fig.6 Comparison of predicted and observed chlorophyll-a concentration in four rivers during the monitoring period of the WT-LSTM model |
| 表 2 4条河流中叶绿素a的Spearman相关性 Tab. 2 Spearman's coefficients of chlorophyll-a among four rivers |
| 表 3 不同河流作为测试集的LSTM模型预测效果 Tab. 3 The prediction effect of LSTM model with different rivers as test sets |
为比较不同时间尺度下模型对叶绿素a浓度预测效果,分别在1~24 h范围内设置多个时间步长的预测任务,并对叶绿素a极大值与平均值的预测效果进行比较. 考虑到澎溪河监测的生物量最高(叶绿素a浓度可维持在25 μg/L以上),此处选取澎溪河数据集为代表测试模型的预测效果.
根据前期研究发现,不同的回溯时间步长对模型的预测效果有较为显著的影响,因此对不同时间尺度的预测任务采取相同的回溯时长以便于比较模型的预测效果,为分析建立合理的预报时长提供依据. 结合模型参数选取实验结果,神经网络层数为2,隐藏神经元个数为40,回溯时间步长为24 h,即利用过去一天的历史数据预测可预测不同时间节点的叶绿素a浓度,预测效果如表 4所示.
| 表 4 WT-LSTM模型在不同时间尺度下澎溪河叶绿素a浓度预测效果 Tab. 4 Prediction effect of chlorophyll-a concentration in the Pengxi River at different time scales using the WT-LSTM model |
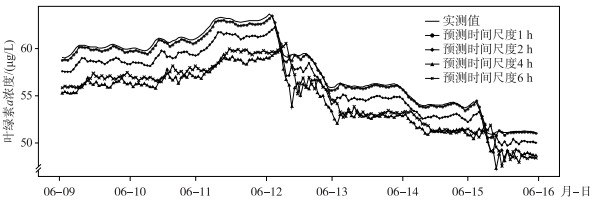
为更直观地比较模型对不同时间尺度的预测效果,在澎溪河水华发生期间(以6月11日-6月17日期间为例)的模型预测值与实测值的对比如图 7所示. 由图 7和表 4可知,短期预测目标下(1~6 h节点),模型的预测精度随着预测时间尺度的增大而降低,表现为RMSE和MRE值增加. 这与赵文喜等[23]在天津海河中的研究结果较为一致. 此外在7~12和13~24 h两个时间尺度预测上,模型对叶绿素a均值的预测精度低于对叶绿素a极值的预测,RMSE计算值分别由2.86和4.38 μg/L,降低到1.45和1.73 μg/L. 可能原因是水华生物量变化是逐步累积过程[24],在时间段内叶绿素a的峰值更容易从历史变化趋势中学习,因而在未来较长时间的尺度预测时,可把预测目标设置为叶绿素a峰值,不仅可简化模型运行步骤,也能达到较好的水华暴发预警效果.
|
图 7 短时尺度(1~6 h)下叶绿素a浓度预测值和实测值对比 Fig.7 Comparison of predicted and measured values of chlorophyll-a concentration under a short time scale (1~6 h) |
通过LSTM与深度置信网络(DBN)比较,说明不同深度学习方法对藻类时序预测结果的适用性. 同样,在相同参数设置前提下,同步评估小波变换处理对两种模型的预测效果影响. 分别采用4条支流数据对模型进行训练与测试,确保使用相同的数据集;但由于LSTM模型的输入张量为三维格式,因而与DBN模型在输入上存在略微的差异.
如表 5所示,针对不同的支流数据,无论是否进行WT降噪处理,LSTM对叶绿素a的预测效果均显著优于DBN,且在香溪河叶绿素a预测的精度最高,其RMSE和MRE分别为0.05 μg/L和0.43 %;相比较下,在草堂河叶绿素a预测的RMSE和MRE的值最大,分别为0.22 μg/L和1.12 %. 在未对样本数据进行WT处理,相较于DBN模型,LSTM模型在4条支流叶绿素a预测的平均RMSE和MRE分别下降了9.20 % 和3.06 %;而样本数据经过WT后,LSTM模型对叶绿素a预测显著升高,较之于DBN模型平均的RMSE和MRE分别下降了51.72 % 和59.24 %. 这一结果与北京空气中PM2.5研究结果较为一致,即在大规模数据学习前提下,LSTM对环境监测的时序数据预测性能要优于传统神经网络方法[25]. Lee等[13]通过比较分析不同的模型对预测叶绿素a浓度的相对性能时发现,基于数理统计的OLS回归分析较深度学习模型表现更差;3种深度学习模型比较时,递归模型(RNN和LSTM)预测性能要优于前馈模型(MLP). 同时,本研究强调在对自动监测数据进行建模处理与预测时,LSTM神经网络相比于传统的人工神经网络(以DBN为例),可有效地挖掘与学习在线时序列信息的长期依赖关系,从而得到理想的预测效果.
| 表 5 DBN和LSTM神经网络在4条河流中的预测效果 Tab. 5 Prediction performance of DBN and LSTM neural networks in four rivers |
此外,结果强调小波降噪处理可显著提高深度神经网络对在线监测数据的预测精度,WT-DBN模型对叶绿素a预测的平均RMSE和MRE分别降低了66.67 % 和70.19 %;而WT-LSTM模型的预测平均RMSE和MRE分别降低了82.28 % 和81.61 %. Xiao等[9]结合小波分析将ANN运用于水华预测,并提出节省成本的单参数方法,实现Siling水库和Winnebago湖中叶绿素a高精度预测,文中指出小波分析集成在神经网络模型中具备如下优势:一是相比于直接预测非线性和非平稳的序列数据,小波分析可以从原始序列中将趋势、周期和噪声等成分提取出来以简化预测过程;二是小波分析可以确保分解后的高分辨率,起到放大细节的效果. 同时,Lu等[26]在利用小波变换对天津于桥水库中叶绿素a日测量时间序列进行分析时指出,分解得到的高频噪声信息可能是受到降雨、风向、水样深度以及测量误差的影响,并且降噪后的叶绿素a时间序列能很好地逼近原始序列. 因此,对于在利用数据驱动的模型分析时,将包含噪声的在线监测数据进行适当的清洗或预处理,能够有效提高模型的预测精度.
3 结论本研究围绕着三峡水库4条支流获取的在线监测数据,结合小波变换与LSTM深度神经网络模型,探索了模型在藻类时序变化短期预测上的应用,具体结论如下:①LSTM神经网络模型在藻类水华短期预测方面有很强的泛化能力. ②对于不同的短时尺度预测任务,LSTM模型向前预测的时间步长越短预测精度越高,在一定的时间区段内对于峰值的预测效果优于均值. ③与传统的深度学习DBN模型相比较,LSTM模型在时间序列的预测上表现更优,若对在线数据进行小波降噪处理后,LSTM模型的优越性则更加明显. 总而言之,本文所探讨的基于在线监测数据与深度神经网络模型的策略,能够有效提取藻类高频率监测的动态特征,且可有效实现一定时段内的叶绿素a峰值的预测,这为三峡水库支流水华的预测提供了一定的实践参考. 同时,实际应用中建议尽可能在研究水域增设站点,通过结合具有统计学关联性的不同空间数据,克服在线监测在藻类空间变化刻画上的局限,增强深度神经网络在训练与测试中的稳健性.
| [1] |
Bao LL, Li XY, Su JJ. Phosphorus cycling and the associated ecological effects of eutrophication in dam-regulated rivers. Acta Ecologica Sinica, 2017, 37(14): 4663-4670. [鲍林林, 李叙勇, 苏静君. 筑坝河流磷素的迁移转化及其富营养化特征. 生态学报, 2017, 37(14): 4663-4670. DOI:10.5846/stxb201603310588] |
| [2] |
Maavara T, Chen QW, van Meter K et al. River dam impacts on biogeochemical cycling. Nature Reviews Earth & Environment, 2020, 1(2): 103-116. DOI:10.1038/s43017-019-0019-0 |
| [3] |
Xia R, Wang GS, Zhang Y et al. River algal blooms are well predicted by antecedent environmental conditions. Water Research, 2020, 185: 116221. DOI:10.1016/j.watres.2020.116221 |
| [4] |
Yang LY, Yang XY, Ren LM et al. Mechanism and control strategy of cyanobacterial bloom in Lake Taihu. J Lake Sci, 2019, 31(1): 18-27. [杨柳燕, 杨欣妍, 任丽曼等. 太湖蓝藻水华暴发机制与控制对策. 湖泊科学, 2019, 31(1): 18-27. DOI:10.18307/2019.0102] |
| [5] |
Ma JR, Deng JM, Qin BQ et al. Progress and prospects on cyanobacteria bloom-forming mechanism in lakes. Acta Ecologica Sinica, 2013, 33(10): 3020-3030. [马健荣, 邓建明, 秦伯强等. 湖泊蓝藻水华发生机理研究进展. 生态学报, 2013, 33(10): 3020-3030. DOI:10.5846/stxb201202140200] |
| [6] |
Rousso BZ, Bertone E, Stewart R et al. A systematic literature review of forecasting and predictive models for cyanobacteria blooms in freshwater lakes. Water Research, 2020, 182: 115959. DOI:10.1016/j.watres.2020.115959 |
| [7] |
Kong WJ, Ma RH, Duan HT. The neural network model for estimation of chlorophyll-a with water temperature in Lake Taihu. J Lake Sci, 2009, 21(2): 193-198. [孔维娟, 马荣华, 段洪涛. 结合温度因子估算太湖叶绿素a含量的神经网络模型. 湖泊科学, 2009, 21(2): 193-198. DOI:10.18307/2009.0206] |
| [8] |
Tong YH, Zhou HL, Huang ZF et al. Time series prediction of the concentration of chlorophyll-a based on RBF neural network with parameters self-optimizing. Acta Ecologica Sinica, 2011, 31(22): 6788-6795. [仝玉华, 周洪亮, 黄浙丰等. 一种自优化RBF神经网络的叶绿素、a浓度时序预测模型. 生态学报, 2011, 31(22): 6788-6795.] |
| [9] |
Xiao X, He JY, Huang HM et al. A novel single-parameter approach for forecasting algal blooms. Water Research, 2017, 108: 222-231. DOI:10.1016/j.watres.2016.10.076 |
| [10] |
Wang L, Zhang TR, Wang XY et al. An approach of improved Multivariate Timing-Random Deep Belief Net modelling for algal bloom prediction. Biosystems Engineering, 2019, 177: 130-138. DOI:10.1016/j.biosystemseng.2018.09.005 |
| [11] |
Yu ZY, Yang K, Luo Y et al. Spatial-temporal process simulation and prediction of chlorophyll-a concentration in Dianchi Lake based on wavelet analysis and long-short term memory network. Journal of Hydrology, 2020, 582: 124488. DOI:10.1016/j.jhydrol.2019.124488 |
| [12] |
Wang XF, Xu LY. Unsteady multi-element time series analysis and prediction based on spatial-temporal attention and error forecast fusion. Future Internet, 2020, 12(2): 34. DOI:10.3390/fi12020034 |
| [13] |
Lee S, Lee D. Four major south Korea′s rivers using deep learning models. International Journal of Environmental Research and Public Health, 2018, 15(7): E1322. DOI:10.3390/ijerph15071322 |
| [14] |
Shin J, Kim SM, Son YB et al. Early prediction of Margalefidinium polykrikoides bloom using a LSTM neural network model in the south sea of Korea. Journal of Coastal Research, 2019, 90(sp1): 236. DOI:10.2112/si90-029.1 |
| [15] |
Torrence C, Compo GP. A practical guide to wavelet analysis. Bulletin of the American Meteorological Society, 1998, 79(1): 61-78. DOI:10.1175/1520-0477(1998)0790061:apgtwa>2.0.co;2 |
| [16] |
Wu QM, Liu ZW, Wang XY et al. Water-bloom forecasting in lakes of Beijing based on wavelet artificial neural network. Computer Engineering and Applications, 2010, 46(12): 233-235. [吴巧媚, 刘载文, 王小艺等. 小波神经网络在北京河湖水华预测中的应用. 计算机工程与应用, 2010, 46(12): 233-235. DOI:10.3778/j.issn.1002-8331.2010.12.070] |
| [17] |
Cai QH, Hu ZY. Studies on eutrophication problem and control strategy in the Three Gorges reservoir. Acta Hydrobiologica Sinica, 2006, 30(1): 7-11. [蔡庆华, 胡征宇. 三峡水库富营养化问题与对策研究. 水生生物学报, 2006, 30(1): 7-11. DOI:10.3321/j.issn:1000-3207.2006.01.002] |
| [18] |
Huang YN, Ji DB, Long LH et al. The variance analysis of characteristics and blooms of the typical tributaries of the Three Gorges reservoir in spring. Resources and Environment in the Yangtze Basin, 2017, 26(3): 461-470. [黄亚男, 纪道斌, 龙良红等. 三峡库区典型支流春季特征及其水华优势种差异分析. 长江流域资源与环境, 2017, 26(3): 461-470. DOI:10.11870/cjlyzyyhj201703017] |
| [19] |
Sun SG, Pang Y, Wang JQ et al. EEMD harmonic detection method based on the new wavelet threshold denoising pretreatment. Power System Protection and Control, 2016, 44(2): 42-48. |
| [20] |
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [21] |
Kingma DP, Adam BJ. A method for stochastic optimization. International Conference on Learning Representations (ICLR), 2015(5). |
| [22] |
Tian WC, Liao ZL, Zhang J. An optimization of artificial neural network model for predicting chlorophyll dynamics. Ecological Modelling, 2017, 364: 42-52. DOI:10.1016/j.ecolmodel.2017.09.013 |
| [23] |
Zhao WX, Zhou B, Liu HL et al. BP neural network-based short-term prediction of chlorophyll concentration inmainstreamof Haihe River. Water Resources and Hydropower Engineering, 2017, 48(11): 134-140. [赵文喜, 周滨, 刘红磊等. 基于BP神经网络的海河干流叶绿素浓度短时预测研究. 水利水电技术, 2017, 48(11): 134-140.] |
| [24] |
Zhu GW, Qin BQ, Zhang YL et al. Variation and driving factors of nutrients and chlorophyll-a concentrations in northern region of Lake Taihu, China, 2005-2017. J Lake Sci, 2018, 30(2): 279-295. [朱广伟, 秦伯强, 张运林等. 2005-2017年北部太湖水体叶绿素a和营养盐变化及影响因素. 湖泊科学, 2018, 30(2): 279-295. DOI:10.18307/2018.0201] |
| [25] |
Zhao JC, Deng F, Cai YY et al. Long short-term memory-Fully connected (LSTM-FC) neural network for PM2.5 concentration prediction. Chemosphere, 2019, 220: 486-492. DOI:10.1016/j.chemosphere.2018.12.128 |
| [26] |
Lu JS, Huang TL, Hu R. Data mining on algae concentrations (chlorophyll) time series in source water based on wavelet. 2008 Fifth International Conference on Fuzzy Systems and Knowledge Discovery, 2008, 5: 611-616. DOI:10.1109/FSKD.2008.540 |
 2021, Vol. 33
2021, Vol. 33 

