(2: 河海大学浅水湖泊综合治理与资源开发教育部重点实验室, 南京 210098)
(3: Department of Division of Hydrologic Sciences, Desert Research Institute, Las Vegas NV 89119)
(4: 张家港市水资源管理处, 张家港 215617)
(2: Key Laboratory of Integrated Regulation and Resource Development on Shallow Lakes, Ministry of Education, Hohai University, Nanjing 210098, P. R. China)
(3: Department of Division of Hydrologic Sciences, Desert Research Institute, Las Vegas NV 89119)
(4: Zhangjiagang City Water Resources Management, Zhangjiagang 215617, P. R. China)
平原河网地区经济发达、人口密集、工业企业聚集、污染源众多,且由于地势平坦,河网水动力条件较差,存在局部往复流和滞流等现象,使得水体抗污染能力弱,水环境整体质量较差[1-2],河道中设置有众多闸、泵站等水工建筑物,水体流动易受调度方式的影响[3]. 引调水则是当前改善平原河网水质较为快捷、经济、可行性较高的技术方法之一[4-5],通过提升水体流动性以增强水体自净能力[6],已在我国海河、太湖、长江、珠江等流域地区中[7-11]得到了广泛应用.
由于平原河网地区复杂的水系、水环境状况与多样化的闸泵调度方式,引调水最终产生的实际效果往往受到多重因素影响. 如何科学有效根据特定目标制定与评估引调水方案,获得较好水环境改善效果,仍有待进一步研究. 目前运用最多的方法是利用野外监测或水环境数值模拟技术,选用一种或几种指标对少量可行性较高的调度方案进行评估优选[12-13]. 该评价方法存在人为主观性大,系统性不足等问题. 卢绪川等[14]通过主成分分析和熵值法所组成的水环境变化情况评价体系对太仓城区河网调水引流方案进行优选,薛联青等[15]建立复杂河网引清流量优化分配模型以实现引清调度优化. 但上述研究中使用的方法涵盖目标较少、没有从引调水后的时间尺度上考量且计算较为复杂,在实际应用中仍存在一定局限.
随着线性规划、多目标优化等方法在引调水中的运用,相关研究重点逐渐转向以水质约束、水资源可持续利用、生态环境效益的多目标评价体系的建立[16]. 这些研究多从流域尺度进行考虑[17],或是运用在湖泊中[18],针对局部复杂河网区域的研究应用仍然相对缺乏.
本研究以太湖流域走马塘东南片平原河网区为研究对象,利用水环境数值模拟技术及多目标优化算法,研究不同引调水方案对区域水环境的改善效果. 构建综合环境与经济效益的多目标函数及评价体系,根据不同目标组合对引调水方案进行精准评估,以期为平原河网地区水环境综合治理提供有效支持.
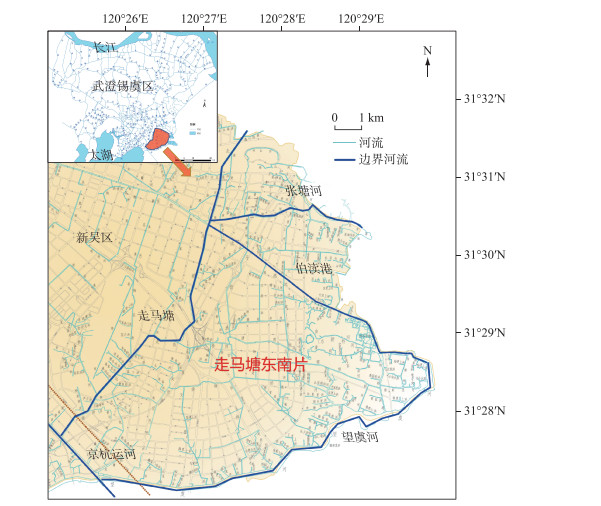
1 研究区域概况走马塘东南片河网区位于无锡市新吴区(图 1),南靠太湖,属太湖流域武澄锡虞区,是典型的江南平原河网地区. 区内河网密布,水资源、水运条件较好,形成了以流域性主干河道望虞河和京杭运河、区域性河道走马塘和伯渎港的“两纵两横”水系构架. 由于该河网区地处无锡市下游,区域内各主干河道也成为了上游污水入境的通道,水质易受京杭运河、伯渎港来水水质影响. 在望虞河西岸控制工程实施后,区域引排水格局由原先向东排入望虞河改为向西排入走马塘、京杭运河,水体流动不畅,污染物聚集,河道水环境现状不容乐观.
|
图 1 走马塘东南片河网区概况 Fig.1 Location of plain river network area of southeast Zoumatang |
采用建立在质量和动量守恒定律基础上的圣维南方程组对一维河道(明渠)非恒定流进行模拟,以流量Q(x,t)和水位Z(x,t)为未知变量,并补充考虑了漫滩和旁侧入流[19-20],基本方程如下:
| $ \left\{\begin{array}{l} \frac{\partial Q}{\partial x}+B_{w} \frac{\partial Z}{\partial t}=q \\ \frac{\partial Q}{\partial t}+2 u \frac{\partial Q}{\partial x}+\left(g \cdot A-B \cdot u^{2}\right) \frac{\partial A}{\partial x}+g \frac{n^{2}|u| Q}{R^{4 / 3}}=0 \end{array}\right. $ | (1) |
式中,Q为流量(m3/s);x、t分别为沿水流方向空间坐标(m)和时间坐标(s);Bw为调蓄宽度(m);Z为水位(m);q为旁侧入流流量(m3/(s ·m));u为断面平均流速(m/s);g为重力加速度(m2/s);A为主槽过水断面面积(m2);B为主流断面宽度(m);n为河道糙率;R为水力半径(m).
按照Abbott-Ionescu六点隐式差分格式离散求解方程组,在每个网格节点按顺序交替计算水位和流量. 将先求解得到的各节点处水位回代至单一河道方程中,最终求得各单一河道各断面水位及流量.
采用基于质量守恒定律的污染物对流扩散方程对水流中污染物的迁移转化进行模拟[21],基本方程如下:
| $ \begin{gathered} \frac{\partial(A C)}{\partial t}+\frac{\partial(Q \cdot C)}{\partial x}-\frac{\partial}{\partial x}\left(A \cdot E x \frac{\partial C}{\partial x}\right)+S_{C}-S=0\left(\text { 其中 } S_{C}=K_{d} \cdot A \cdot C\right) \end{gathered} $ | (2) |
| $ \sum\limits_{I=1}^{N I}(Q \cdot C)_{I, j}=(C \Omega)_{j}\left(\frac{\mathrm{d} \mathrm{Z}}{\mathrm{d} t}\right)_{j} $ | (3) |
式中,Q为流量(m3/s),Z为水位(m);A为河道面积(m2);Ex为纵向分散系数(m2/s);C为水流输送的物质浓度(mg/L);Ω为河道叉点-节点的水面面积(m2);I、j分别为节点编号以及与该节点相连接的河道编号;SC为与输送物质浓度有关的衰减项;Kd为衰减因子;S为外部的源或汇项.
求解方程时,时间项采用向前差分,对流项采用上风格式求解,扩散项采用中心差分格式.
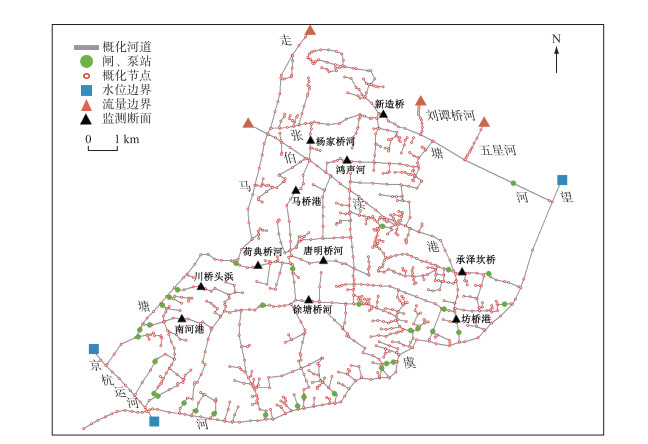
本研究以2019年无锡市新吴区水系现状图为基础,精密至村级河道,共概化河道213条,设置河道节点1222个,设置闸、泵站共54个,河网概化及监测断面分布情况见图 2.
|
图 2 研究区域河网概化及监测断面分布 Fig.2 River network summarization and the monitoring sections of the study area |
模型以走马塘、刘谭桥河、五星河、伯渎港设置流量边界;京杭运河、望虞河设置水位边界,其中京杭运河东边界、伯渎港为出流,其余均为入流,断头河全部设置为闭边界. 初始水位设置为3.4 m,初始流量设置为0.1 m3/s.
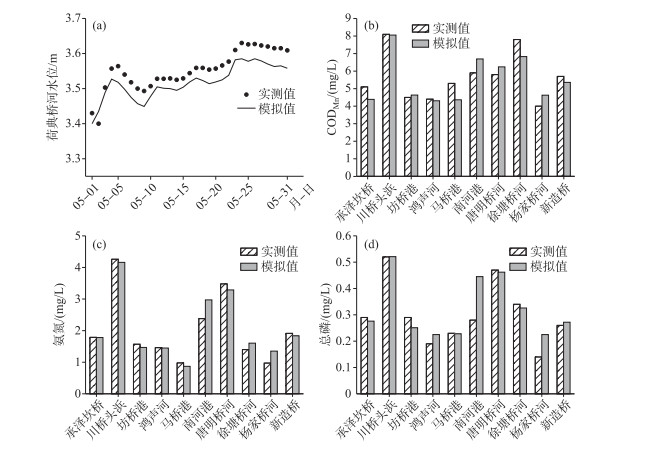
2.2 模型率定验证根据2017年5-6月的监测数据对模型进行参数率定,根据2018年5-6月同一区域监测数据对模型进行验证. 结果表明,走马塘东南片河道糙率在0.02~0.04之间,CODMn、氨氮、总磷的综合衰减系数分别为0.08~0.11、0.05~0.08、0.06~0.09 d-1[22]. 由水动力模型(图 3)与水质模型(表 1,图 3)验证结果可看出,计算模拟结果与实测值拟合较为良好,水位绝对误差(AE)为4 cm,均方根误差(RMSE)为0.0464,小于0.05;水质平均相对误差(RE)小于15 %,RMSE小于0.7,能够满足对研究区域河网进行模拟的要求.
|
图 3 水动力、水质验证结果: (a)荷典桥河水位、(b)CODMn、(c)氨氮和(d)总磷 Fig.3 Validation results of the hydrodynamic and water quality model: (a)water level of Hedianqiao River, (b)CODMn, (c)ammonia nitrogen and (d)total phosphorus |
| 表 1 水质验证结果 Tab. 1 Validation results of the water quality model |
走马塘东南片河网中有众多闸、泵站等水工建筑物,河道水体流动状态同时受自然条件和水利工程影响. 根据不同闸、泵组合开闭方式可制定多种引调水方案. 现选取区域内水质较差的5月份为研究时段,制定引调水方案,并利用构建的模型对各方案进行模拟计算.
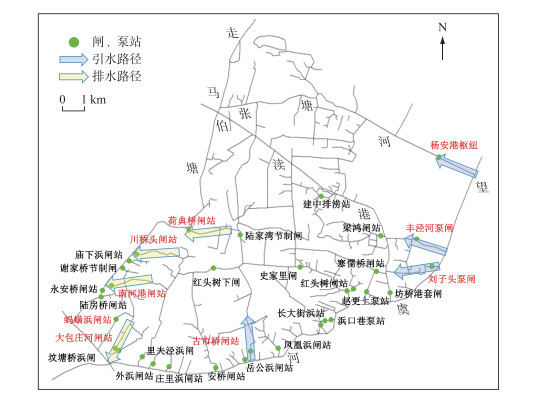
研究区内主要引水水源为望虞河,望虞河全年平均水质为Ⅲ类,水质较好,2017年CODMn、氨氮、总磷平均浓度分别为4.11、0.36、0.13 mg/L. 针对近期及规划制定了8个引调水方案,其中方案零为近期方案,望虞河沿线各泵站流量均按现状流量设置. 方案一~方案七为规划方案,望虞河沿线各泵站流量按照不同规划情景设置,规划方案又分为泵引自排、泵引泵排2种组合. 各方案中,东部望虞河沿线除3个泵站开泵向内部引水外,其余沿线闸站、泵站均处于关闭状态;西部走马塘沿线除南河港闸站处于常开状态,以及规划方案泵引泵排组合方案中设置排水时打开荷典桥泵站、川桥头泵站外,其余闸站、泵站均处于关闭状态. 参考无锡市锡澄片区畅流活水规划以及无锡市新吴区畅流活水规划中所推荐的引调水调度周期,将本研究中各方案总模拟计算时长均设置为5 d. 各方案主要闸、泵站开闭组合见表 2,主要闸、泵站分布及引排水路径见图 4.
| 表 2 各方案主要闸、泵站调度组合 Tab. 2 Scheduling combination of main sluices and pump stations in each scheme |
|
图 4 研究区域主要闸、泵站及引排水路径分布 Fig.4 The main sluices and pump stations and the diversion and drainage routes in the study area |
根据引调水目的与欲取得的效果,当前研究多从水质改善、水动力改善、经济效益3个方面对引调水工程进行评估. 其中水质改善主要分为提升水质改善效果与提升水质达标率两个方面;水动力改善主要包括提升水体更新速度,缩短水体置换周期等;经济效益主要为降低引调水过程中的经济耗费,同时确保具有较好的水质改善效果[18, 23-24]. 本研究选取水质与经济2个方面进行综合考虑,筛选CODMn、氨氮、总磷3项污染物作为评价指标构成环境效益函数,将引调水水量与经济费用挂钩构成经济效益函数.
采用多目标优化的评价方法(式(4))以权衡调水过程中的环境效益和经济效益[25-26],通过建立评价体系筛选出水质改善效果相对较好且经济耗费较低的引调水方案,进而获得水量水质优化调控方案.
| $ \min y(i)=\frac{E_{i}-\bar{E}}{S_{\mathrm{E}}}+\frac{M_{i}-\bar{M}}{S_{\mathrm{M}}} $ | (4) |
式中, y(i)为多目标函数,i代表各个引调水工况,不同工况对应不同的引调水水量,Ei为环境效益函数,Mi为经济效益函数[27],当y(i)取得最小值时,环境效益和经济效益都达到相对较理想值,即为最优解.
环境效益函数与经济效益函数的多目标评价体系包含以下3层(表 3):
| 表 3 多目标评价体系组成 Tab. 3 The composition of multi-objective evaluation system |
第一层为指标层,分为以下2种情况:1)各项水质指标(CODMn、氨氮、总磷)采用相同权重;2)根据水质指标污染严重程度赋权,并用欧式距离对污染严重程度进行描述,单项指标改善率与综合指标改善率越接近,代表污染越易控制,并为其赋权重wi,计算方法如式(5)~(7).
| $ l_{i}=\left\{\begin{array}{l} x_{i j}-y_{j}, x_{i j} <y_{j} \\ 0, x_{i j}>y_{j} \end{array}\right. $ | (5) |
| $ L_{i}=\sqrt{\sum\limits_{j=1}^{n} l_{i}^{2}} $ | (6) |
| $ w_{i}=\frac{L_{i}}{\sum L_{i}} $ | (7) |
式中,当为水质指标赋权时,i代表水质指标类别,包括CODMn、氨氮、总磷3项,j代表n个工况,xij代表第i项水质指标在第j个工况下的改善率,yj代表第j个工况下的水质综合改善率;当为空间点位赋权时,i代表点位编号,共有1、2、3、…、9个点位,j代表n个工况,xij代表第i个点位在第j个工况下的改善率,yj代表第j个工况下的水质综合改善率.
第二层为空间层,分为以下3种情况:1)各监测断面点位采用相同权重;2)偏向污染较为严重的断面点位. 同样基于水质指标改善率计算权重,计算方法同上(式(5)~(7));3)考核断面优先.“水十条”中要求强化水质目标管理,因而当前实际治理方案及研究多集中在保障考核断面水质优先达标上[28-29]. 参考《无锡市“两减六治三提升”专项行动工作方案》中对重点断面达标率的要求,对考核断面赋优先权重80 %,其余断面权重为20 %.
第三层为决策层,本研究采取以提升水质改善效果为决策目标,环境效益函数基于水质改善率计算,水质改善率基于综合污染指数法计算,计算各项水质指标的单指数,并以各单指数之和为综合指数(式(8)),环境效益函数在此采用负向标准化;经济效益函数基于引调水水量计算(式(9)).
| $ R_{j}=\frac{P_{0}-P_{j}}{P_{0}} \times 100 \% $ | (8) |
式中,Rj为水质改善率,P0为引调水前水质指数,Pj为工况j下的水质指数.
| $ M=0.126 Q $ | (9) |
式中,M为引调水经济费用(百万/年);Q为引调水流量(m3/s).
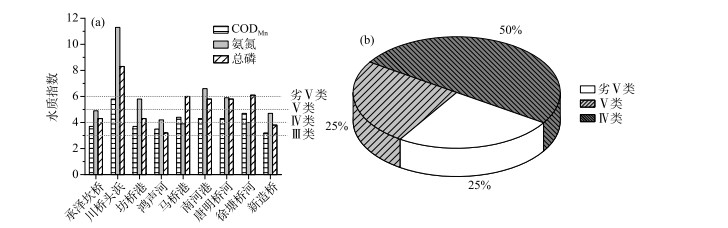
3 结果与讨论 3.1 引调水对水环境改善效果评估选取均匀分布于研究区域内的9个监测断面(图 2)对引调水前后水质进行分析. 其中承泽坎桥断面为省考断面,水质目标为Ⅲ类,其余断面水质目标均为Ⅳ类. 运用单因子水质标识指数法对引调水前水质进行评价,评价指标为CODMn、氨氮、总磷. 由结果可看出(图 5),引调水前区域整体水质较差,有50 % 的断面水质为Ⅳ类,25 % 为Ⅴ类,还有25 % 为劣Ⅴ类. 3个水质指标中,总磷与氨氮污染较为严重,分别有55.6 %、44.4 % 的断面水质劣于Ⅳ类,CODMn污染相对较轻,有11.1 % 的断面水质劣于Ⅳ类. 区域西南部排水出口处及西北部断面污染较其余断面更严重.
|
图 5 引调水前水环境状况: (a)水质指数,(b)断面水质类别比例 Fig.5 Water environment quality of the study area before the water diversion: (a)water quality index, (b)proportion of water quality categories of the sections |
实施近期方案零引调水5 d后,67 % 断面处氨氮浓度、56 % 断面处总磷浓度以及44 % 断面处CODMn浓度均较引水前上升,且3项指标浓度平均上升幅度分别为26.2 %、45.2 %、11.3 %,平均改善率分别为-4.3 %、-9.9 %、12.0 %. 引水后,区域内主要污染因子氨氮、总磷在大部分断面处浓度并未降低而是出现上升的趋势. 这是由于方案零总引调水流量较小,仅4 m3/s,实施引调水会将上游河段中的污染物冲刷至下游河道导致污染物积累,进而造成河道中污染物浓度升高,对水质改善带来负效应. CODMn则由于污染相对较轻,在部分断面浓度上升情况下平均浓度呈下降趋势,改善率仍为正值. 因此,近期引调水方案零对研究区域河网水环境改善效果并不理想,甚至存在负效应,在后续研究中仅针对制定的规划引调水方案进行讨论.
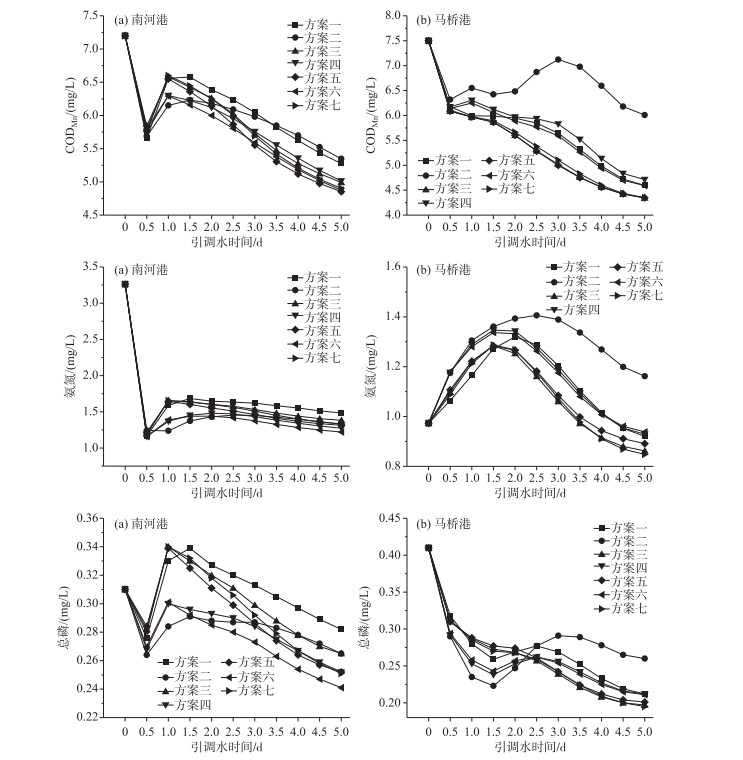
选取污染较严重的南河港、马桥港2个断面分析各规划方案引调水后水质改善效果,如图 6所示,引调水对两断面处水质改善效果较明显,且改善效果基本随引水时间增长而提升. 南河港断面在引调水初期,CODMn、氨氮、总磷浓度均呈现较大幅度下降趋势,但以0.5 d为拐点又出现上升,在各方案均上升到峰值后最终呈现逐渐下降趋势,直至第5天降至较低值. 主要由于该断面位于西南排水出口,在此堆积聚集污染物较多,开始引调水后清水从东部汇入,较大提升了区域河道水体流动性,使该处原有高浓度污水团直接经排水出口被置换转移至下游,污染物浓度得以暂时降低. 但随引水时间增长,上游河道中污染物逐渐随引水被冲刷至该处,导致污染物浓度再次上升. 上游带来污染物的负效应随引水时间增长逐渐抵消,水质浓度得以再次降低. 相比之下,马桥港断面处CODMn、总磷浓度在引调水后大体呈现逐渐降低的态势,但部分方案存在浓度反弹现象,方案二反弹现象最明显. 该处氨氮浓度在引调水后则直接呈现先上升后下降的趋势,主要由于该断面氨氮本底浓度相对较低,上游来引水中氨氮浓度较此处更高,同时在传输过程中携带了上游的污染物,到达此处后便造成氨氮浓度上升,但随引水时间增长,上升至浓度峰值后也呈现下降趋势. 方案二中3种污染物浓度上升幅度最大,这可能是由于马桥港断面位于西北部,距东部引水入口较远,上游到达清水有限. 同时,方案二由东部引入的清水水量相对较小,且打开西部泵站进行抽水,抽引了上游河道的污染物在此处聚集,东部而来有限的清水对此处水质改善作用不足,进而造成污染物浓度上升. 以上现象同样也出现在太湖流域湖西区河网引调水实验[30]与杭州市江干区内河网引水模拟实验中[31],引调水初期的水质改善效果较大程度会受到上游河网污染源分布及河道本底污染物浓度的影响. 同时,调度模式也会影响污染物在河网中的迁移转化路径,使得同一断面处的水质改善过程存在异质性.
|
图 6 引调水过程中CODMn、氨氮、总磷浓度变化: (a)南河港、(b)马桥港 Fig.6 The change of CODMn, ammonia nitrogen, total phosphorus concentrations during water diversion: (a)Nanhegang, (b)Maqiaogang |
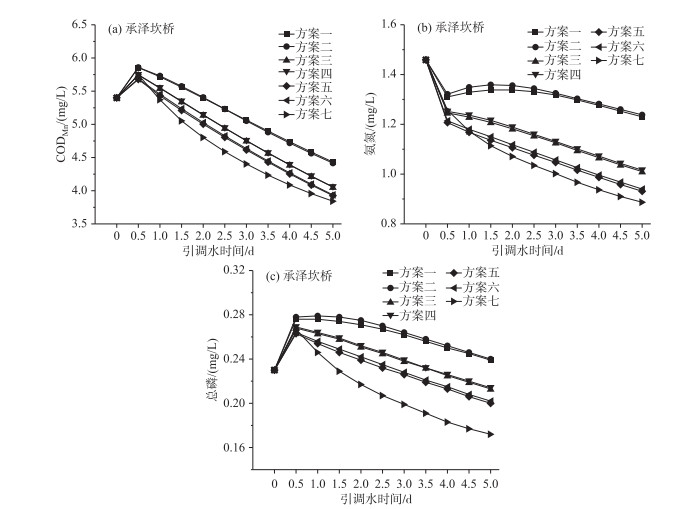
选取研究区域内省考断面承泽坎桥进行分析,如图 7所示,该处CODMn、总磷浓度在引调水后呈现先上升后下降的趋势,以0.5 d为下降拐点;氨氮浓度则基本呈现逐渐下降趋势,但方案一、方案二在0.5 d后出现浓度反弹现象,且在引调水5 d后的浓度较其余方案更高,改善效果不明显. 以上现象同样是由于断面上游河道中CODMn、总磷浓度较高, 污染源较多造成的. 上游处氨氮浓度则相对较低,但方案一、二总引调水流量分别为10、19.55 m3/s,相对较小,对水流动力改善效果有限,且在方案二中开启西部泵站抽水后可能增加了对上游河水中污染物的抽引作用,导致出现氨氮浓度再次上升的现象.
|
图 7 引调水过程中承泽坎桥断面水质指标浓度变化: (a)CODMn、(b)氨氮和(c)总磷 Fig.7 The change of the water quality indexs concentrations of Chengzekanqiao section during water diversion: (a)CODMn, (b)ammonia nitrogen and (c)total phosphorus |
由此可见,规划方案中增加引调水流量以及改变调度模式后,能够在一定程度上改善区域水环境,规划方案下引调水5 d后,CODMn、氨氮、总磷的平均改善率分别为30.7 %、22.2 %、26.4 %. 但是,不同或相同方案下,河网中不同监测断面、不同指标之间的水质改善过程与效果、对时间的响应,都存在一定异质性,借助常规分析评价方法较难对各方案的综合改善效果进行评估与区别. 因此,充分考虑引调水过程中各类异质性因子,采用建立的平原河网引调水多目标评价体系对各方案进行评估分析,获得水量水质优化调控方案存在必要性.
3.2 多目标最优引调水工况根据引调水方案与时长进行编号,组成不同的引调水工况. 以每0.5 d作为一个引调水单位时间长度,如工况2-6代表方案二引水3 d,以此类推,在不考虑近期引调水方案下共有70个工况,根据各工况总引调水水量对各方案进行排序.
根据评价体系计算得出的各水质指标与空间点位权重见表 4. 由赋权结果可看出,在以提升水质改善率为决策目标时,总磷是研究区域内的重点控制指标,其次是CODMn,最后是氨氮;在空间点位权重分配上,鸿声河断面与新造桥断面是最需要重点控制的断面,其次是坊桥港断面与承泽坎桥断面.鸿声河与新造桥断面均位于区域西北部,距东部引水入口较远,由东侧而来的引水若流量较小,到达两处的水量将会十分有限,进而造成水质改善效果有限,导致两断面获得权重较大.
| 表 4 水质指标和空间点位权重 Tab. 4 The weight of water quality indexes and spatial points |
利用所得权重与多目标函数对各工况结果进行优化计算,得到以下结果:
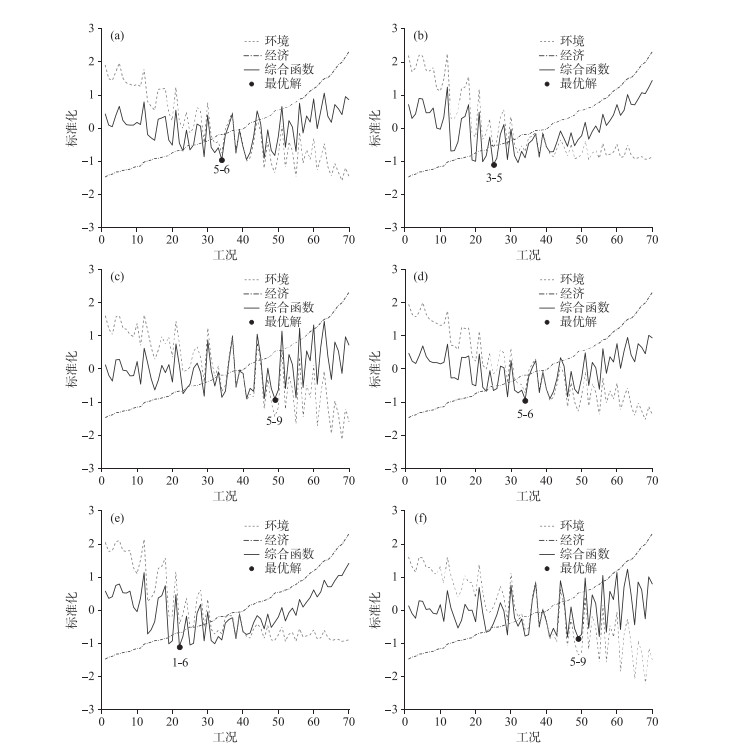
1) 各水质指标采用相同权重:①空间点位采用相同权重,如图 8a所示,此时工况5-6,即方案五引水3 d为最优工况;②偏向污染严重点位,针对污染严重情况为断面赋权,如图 8b,此时工况3-5,即方案三引水2.5 d为最优工况;③考核断面优先,为考核断面承泽坎桥优先赋权重80 %,如图 8c,此时工况5-9,即方案五引水4.5 d为最优工况.
|
图 8 多目标函数最优解: (a)、(d)空间点位采用相同权重,(b)、(e)偏向污染严重点位,(c)、(f)考核断面优先 Fig.8 The optimal solutions of the multi-objective function: (a) and (d) the same weight is applied to the spatial points, (b) and (e) the weight is biased towards heavily polluted points, (c) and (f) the examination section is preferred |
2) 偏向污染严重水质指标,为水质指标进行赋权:①空间点位采用相同权重,如图 8d所示,此时工况5-6,即方案五引水3 d为最优工况;②偏向污染严重点位,针对污染严重情况为断面赋权,如图 8e,此时工况1-6,即方案一引水3 d为最优工况;③考核断面优先,为考核断面承泽坎桥优先赋权重80 %,如图 8f,此时工况5-9,即方案五引水4.5 d为最优工况.
3) 以考核断面达标为前提:由于承泽坎桥为省考断面,若在引调水时优先考虑其水质达标,排除不能使其水质达标的引调水工况后再利用多目标函数进行工况优选,此时可得到以考核断面达标为前提的最优工况. 该前提下筛选出的最优工况均为工况7-7,即方案七引水3.5 d. 以上3种情况下的最优工况见表 5.
| 表 5 基于多目标优化的最优工况 Tab. 5 The optimal schemes under the multi-objective optimization |
综合不同目标下最优工况对应方案的闸、泵站调度组合可看出,采用建立的多目标评价体系优选出的工况与设定目标之间具有一定一致性. 当对各监测断面点位采取相同权重,各水质指标采取相同权重或偏向污染严重的水质指标时所对应最优工况均为5-6;当以考核断面优先为目标时,对应的最优工况均为5-9,该工况对应的方案五中将考核断面所在河道上丰泾河泵闸一线的引调水流量设置为4 m3/s,相对较大,但低于方案三、四、七中所设置的最大流量5 m3/s. 由于已将考核断面处权重设置为80 %,优先考虑该断面水质改善效果.同时,该断面距离引水入口较近,故在相对较大的引调水流量下便能获得较好改善效果,并对应相对较低的经济耗费;当以考核断面达标为前提进行二次优选时,对应最优工况均为7-7. 该工况对应方案中将考核断面所在河道一线引调水流量增至5 m3/s,将区域东部丰泾河泵闸、刘子头闸站引调水流量分别增大至5、2 m3/s,并适度减少其余线路流量. 使得由东部主要引水线路进入河网中部的清水水量增加,西部泵站抽排水也加速了引水在河网内移动速度,两者共同作用下对监测断面分布较多的河网中部水质改善效果提升较大,进一步使区域整体的水质平均改善率提升.同时由于总引调水量较小,对应经济耗费也较低.
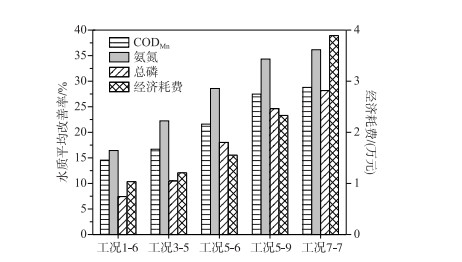
各最优工况下河网中水质指标平均浓度见表 6,CODMn、氨氮、总磷平均浓度分别为5.35、1.22、0.23 mg/L,平均水质类别由引调水前的劣Ⅴ类提升至Ⅳ类. 水质指标改善率与经济耗费见图 9. 5种不同目标工况下河网水质平均改善率分别为12.8 %、16.5 %、22.7 %、28.8 %、31.0 %,经济耗费分别为1.04万、1.21万、1.55万、2.33万、3.89万元,较高的改善率对应相对较高的经济耗费. 除以考核断面达标为前提,不同目标下最优工况对应方案均为泵引自排方案. 尽管泵引泵排方案能够加快引水在河网内的移动速度,但增加抽排水所产生的经济耗费大于提升的环境效益,这与卢绪川等[14]在太仓城区河网调水模拟实验中发现的现象类似. 引调水产生的环境效益受到调度模式、引调水水量、引水水质的共同影响,改变其中一个或两个因素对于引调水后水质改善效果的提升可能是有限的.
| 表 6 多目标最优工况水质平均浓度 Tab. 6 The water quality indexs concentrations of the optimal schemes under the multi-objective optimization |
|
图 9 多目标最优工况水质平均改善率与经济耗费 Fig.9 The water quality improvement rates and the economic costs of the optimal schemes under the multi-objective optimization |
在平原河网引调水实际操作中,受水区域往往较为复杂,不同水质指标、不同区域之间污染情况多存在较大差异. 已有研究在评估优选引调水方案时多以不同监测点位的水质代表所在河段水质,并多以不同河段几种水质指标的平均改善效果作为评价标准[24, 31]. 这不能较好地概括出整个区域中水体污染存在的异质性,并且可能导致最终优选的方案因兼顾因素过多造成经济成本较大. 利用本研究中构建的多目标评价体系,充分考虑河网中不同水质指标的污染差异以及不同区域污染的空间差异,对不同指标及空间点位进行赋权,能够针对性考虑引调水过程中需要重点改善的因素,相较于常规的等权重处理可以更好地减小调度过程中的经济耗费.
不同调度方案下,平原河网引调水过程中的环境效益与经济效益均存在异质性,借助本研究建立的引调水多目标评价体系,可以准确筛选出特定目标下的最优引调水工况. 优选工况对应方案与设定目标之间具有一定的一致性. 由于河道中本底污染物与岸上污染物的存在,引调水可能会对下游河道的水质造成负效应. 因此仅采取引调水改善河网水环境存在局限性,不能从根源上消除水体污染. 为获得较好的水环境改善效果与较低的经济耗费,引调水应尽量在已实施控源截污前提下实行.
4 结论本研究构建太湖流域走马塘东南片平原河网区一维水动力水质模型,探讨不同引调水方案对区域水环境的改善效果,并从决策目标、水质指标、空间指标3个层面综合考虑,构建以环境效益与经济效益函数相结合的多目标函数及评价体系,对不同引调水方案进行评估优选,确定出不同目标组合下的最优化调度方案,主要结论如下:
1) 较小引调水流量下对研究区河网水环境改善效果十分有限. 引调水流量较大时,能够在一定程度上改善区域水环境状况,规划方案下引调水5 d后,研究区域中CODMn、氨氮、总磷的平均改善率分别为30.7 %、22.2 %、26.4 %.
2) 不同或相同方案下,研究区域河网中不同空间点位、不同水质指标之间的水质改善过程与效果都存在一定异质性. 在以提升水质改善率为决策目标时,总磷是研究区域内的重点控制指标,距离引水水源入口较远的鸿声河与新造桥断面是最需要重点控制的断面.
3) 在平原河网引调水方案制定过程中,引调水水量和调度模式都会对河网区水质产生差异性影响,采用数值模拟方法进行前置规划十分必要,在模拟时还应结合河岸控源截污工程实施进度,将上游污染源分布精准纳入到模型边界条件中.
4) 本研究建立引调水多目标函数与评价体系,将引调水过程中存在的指标与空间差异性进行分类概括,综合考虑决策目标、水质指标、空间指标等因子,能够从多个层面对不同引调水方案进行评估与优选,得到综合考虑环境效益与经济效益的最优方案,为平原河网地区水环境长效管理与科学决策提供理论参考.
| [1] |
Jia HF, Yang C, Zhang YH et al. Simulations of a water quality improvement for urban river networks. Journal of Tsinghua University: Science and Technology, 2013, 53(5): 665-672. [贾海峰, 杨聪, 张玉虎等. 城镇河网水环境模拟及水质改善情景方案. 清华大学学报: 自然科学版, 2013, 53(5): 665-672.] |
| [2] |
Li YP, Acharya K, Stone MC et al. Spatiotemporal patterns in nutrient loads, nutrient concentrations, and algal biomass in Lake Taihu, China. Lake and Reservoir Management, 2011, 27(4): 298-309. DOI:10.1080/07438141.2011.610560 |
| [3] |
Li CQ, He WX, Chen DY. The scheme design of water diversion and distribution for improving water environment in the flat river network. China Rural Water and Hydropower, 2012(7): 45-47. [李茶青, 何文学, 陈冬云. 平原河网区改善水环境引水配水方案设计. 中国农村水利水电, 2012(7): 45-47.] |
| [4] |
Lu XC, Li YP, Huang DJ et al. Study on water diversion schemes for improvement of hydrodynamics in plain river network. Water Resources and Power, 2015, 33(4): 93-95. [卢绪川, 李一平, 黄冬菁等. 平原河网调水引流水动力改善效果分析. 水电能源科学, 2015, 33(4): 93-95.] |
| [5] |
Liu B, Sheng M, Zhu Q et al. Migration and transformation of nitrogen in urban stream located in plain river-net area based on water resources regulation. Environmental Science, 2014, 35(9): 3373-3380. [刘波, 盛明, 朱强等. 基于水资源调度的平原河网区城市河道氮迁移转化研究. 环境科学, 2014, 35(9): 3373-3380.] |
| [6] |
Xu YX, Li YP, Luo YC et al. Effect evaluation of water diversion to water quality improve in plain tidal river network. Water Resources Protection, 2019, 35(6): 124-130. [许益新, 李一平, 罗育池等. 引水改善平原感潮河网水质效果评估. 水资源保护, 2019, 35(6): 124-130.] |
| [7] |
Jin XN. Research on integrated regulation of water quality and water quantity in plain river-net areas[Dissertation]. Tianjin: Tianjin University, 2017. [金相楠. 平原河网地区水质水量综合调控研究[学位论文]. 天津: 天津大学, 2017. ]
|
| [8] |
Li YP, Acharya K, Yu ZB. Modeling impacts of Yangtze River water transfer on water ages in Lake Taihu, China. Ecological Engineering, 2011, 37(2): 325-334. DOI:10.1016/j.ecoleng.2010.11.024 |
| [9] |
Zhu XL, Li YP, Xu YX et al. Effects of time scale on simulation accuracy of hydrodynamic water quality of tidal river network. Water Resources Protection, 2020, 36(3): 67-75. [朱晓琳, 李一平, 许益新等. 时间尺度对平原感潮河网水动力水质模拟精度的影响. 水资源保护, 2020, 36(3): 67-75.] |
| [10] |
Xia K, Wang H, Qin WH et al. Assessment on effects of water quality improvement in Inner Qinhuai River by water dispatching. Water Resources Protection, 2015, 31(2): 74-78. [夏琨, 王华, 秦文浩等. 水量调度对内秦淮河水质改善的效应评估. 水资源保护, 2015, 31(2): 74-78.] |
| [11] |
Du J, Chen XH, Chen ZH et al. Water diversion and control for water environment in tidal network of Pearl River Delt. Journal of China Hydrology, 2012, 32(4): 16-21. [杜建, 陈晓宏, 陈志和等. 珠江三角洲感潮河网区水环境引水调控研究. 水文, 2012, 32(4): 16-21. DOI:10.3969/j.issn.1000-0852.2012.04.004] |
| [12] |
Jiang T, Zhu SL, Zhang Q et al. Numerical simulation on effects of gate-pump joint operation on water environment in tidal river network. Journal of Hydraulic Engineering, 2011, 42(4): 388-395. [江涛, 朱淑兰, 张强等. 潮汐河网闸泵联合调度的水环境效应数值模拟. 水利学报, 2011, 42(4): 388-395.] |
| [13] |
Xu GQ, Tang YZ. Research on the optimization of clean water diversion on Chongming Island. China Rural Water and Hydropower, 2011(2): 4-7. [徐贵泉, 唐迎洲. 崇明岛引清调水方式优化研究. 中国农村水利水电, 2011(2): 4-7.] |
| [14] |
Lu XC, Li YP, Huang DJ et al. Study on optimistic plan of water transfer and diversion in plain river network//Wu YS, Tang HW, Wang C eds. Proceedings of The 27th National Conference on Hydrodynamics(volume two). Beijing: China Ocean Press, 2015: 561-568. [卢绪川, 李一平, 黄冬菁等. 平原河网区调水引流优化方案研究//吴有生, 唐洪武, 王超编. 第27届全国水动力学研讨会文集(下册). 北京: 海洋出版社, 2015: 561-568. ]
|
| [15] |
Xue LQ, Wang SQ, Xing BL et al. Flow allocation optimization model of clean water diversion in complex river networks. Water Resources Protection, 2014, 30(5): 68-72. [薛联青, 王思琪, 邢宝龙等. 复杂河网引清流量优化分配模型. 水资源保护, 2014, 30(5): 68-72.] |
| [16] |
Peng ZY, Zhang LL, Yin JX et al. Advance and prospect of study on joint regulation of water quality and quantity. Water Resources and Hydropower Engineering, 2015, 46(4): 6-10. [彭卓越, 张丽丽, 殷峻暹等. 水质水量联合调度研究进展及展望. 水利水电技术, 2015, 46(4): 6-10.] |
| [17] |
Dong ZC, Bian GY, Wang CH et al. Joint operation of water quantity and quality based on numeeical model. Advances in Water Science, 2009, 20(2): 184-189. [董增川, 卞戈亚, 王船海等. 基于数值模拟的区域水量水质联合调度研究. 水科学进展, 2009, 20(2): 184-189. DOI:10.3321/j.issn:1001-6791.2009.02.005] |
| [18] |
Hua Z L, Gu L, Xue H et al. Assessing indicators for water diversion based on improving water quality of shallow lakes. J Lake Sci, 2008, 20(5): 623-629. [华祖林, 顾莉, 薛欢等. 基于改善水质的浅水湖泊引调水模式的评价指标. 湖泊科学, 2008, 20(5): 623-629. DOI:10.18307/2008.0511] |
| [19] |
Lu SQ, Xu ZX. Hydrodynamic model for plain river networks and its solution. Water Resources Protection, 2003(3): 5-9. [卢士强, 徐祖信. 平原河网水动力模型及求解方法探讨. 水资源保护, 2003(3): 5-9. DOI:10.3969/j.issn.1004-6933.2003.03.002] |
| [20] |
Xiang XH, Wu XL, Niu S et al. Construction of one-dimensional river network model based on explicit finite volume method. Advances in Science and Technology of Water Resources, 2015, 35(4): 6-9. [向小华, 吴晓玲, 牛帅等. 基于显式有限体积法的一维河网模型. 水利水电科技进展, 2015, 35(4): 6-9.] |
| [21] |
Pang Y, Wang YY, Hu QY. Research on water quality improvement scheme for a typical river in Wenhuang Plain in Zhejiang Province. Water Resources Protection, 2016, 32(2): 100-105. [逄勇, 王瑶瑶, 胡绮玉. 浙江温黄平原典型河流水质改善方案研究. 水资源保护, 2016, 32(2): 100-105.] |
| [22] |
Feng S, Li XY, Deng JC. Determination of comprehensive pollutants attenuation coefficents of plain river networks in the upper reaches of Lake Taihu Basin. Acta Scientiae Circumstantiae, 2017, 37(3): 878-887. [冯帅, 李叙勇, 邓建才. 太湖流域上游平原河网污染物综合衰减系数的测定. 环境科学学报, 2017, 37(3): 878-887.] |
| [23] |
Lu XY, Wu SQ, Zhang Y et al. Progress of ecology and environment effect of water diversion project. Journal of Water Resources and Water Engineering, 2015, 26(4): 38-45. [吕学研, 吴时强, 张咏等. 调水引流工程生态与环境效应研究进展. 水资源与水工程学报, 2015, 26(4): 38-45.] |
| [24] |
Zhang HL, He XC, Deng JQ. Regulation of hydrodynamics and water quality in tidal river network based on gate-pump joint operation. Journal of Yangtze River Scientific Research Institute, 2019, 36(8): 36-41, 48. [张海丽, 贺新春, 邓家泉. 基于闸泵联控的感潮河网区水动力水质调控. 长江科学院院报, 2019, 36(8): 36-41, 48.] |
| [25] |
Farmani R, Savic DA, Walters GA. Evolutionary multi-objective optimization in water distribution network design. Engineering Optimization, 2005, 37(2): 167-876. DOI:10.1080/03052150512331303436 |
| [26] |
Xevi E, Khan SA. A multi-objective optimisation approach to water management. Journal of Environmental Management, 2005, 77(4): 269-277. DOI:10.1016/j.jenvman.2005.06.013 |
| [27] |
Tang CY. Mathematical model for water environment setup and application based on the internal nutrient release and parametric optimization in Lake Taihu[Dissertation]. Nanjing: Hohai University, 2015. [唐春燕. 基于内源释放与参数优化技术的太湖水环境数学模型及应用[学位论文]. 南京: 河海大学, 2015. ]
|
| [28] |
Shan BQ, Wang C, Li XY et al. Method for river pollution control plan based on water quality target management and the case study. Acta Scientiae Circumstantiae, 2015, 35(8): 2314-2323. [单保庆, 王超, 李叙勇等. 基于水质目标管理的河流治理方案制定方法及其案例研究. 环境科学学报, 2015, 35(8): 2314-2323.] |
| [29] |
Song WW, Pang Y. The calculation of water environment capacity of Qinhuai River Basin based on the national test of QB-CS water quality standards. China Rural Water and Hydropower, 2017(10): 80-84. [宋为威, 逄勇. 基于国考七桥瓮断面水质达标秦淮河流域水环境容量计算. 中国农村水利水电, 2017(10): 80-84. DOI:10.3969/j.issn.1007-2284.2017.10.016] |
| [30] |
Wang YY, Liu ZX, Ma NL et al. Research on water resourcs dispatching scheme design for complex river-lake-connected areas. China Rural Water and Hydropower, 2019(4): 1-7. [王元元, 刘增贤, 马农乐等. 复杂江河湖连通地区引清调度方案设计研究. 中国农村水利水电, 2019(4): 1-7. DOI:10.3969/j.issn.1007-2284.2019.04.001] |
| [31] |
Chen ZT, Hua L, Jin QN. Assessing the efficacy of water diversion to improve water quality in city river network. Journal of Yangtze River Scientific Research Institute, 2015, 32(7): 45-51. [陈振涛, 滑磊, 金倩楠. 引水改善城市河网水质效果评估研究. 长江科学院院报, 2015, 32(7): 45-51.] |
 2021, Vol. 33
2021, Vol. 33 


