(2: 清华大学水利水电工程系, 水沙科学与水利水电工程国家重点实验室, 北京 100084)
(2: State Key Laboratory of Hydro-science and Engineering, Department of Hydraulic Engineering, Tsinghua University, Beijing 100084, P. R. China)
采用数学模型模拟河流水质过程是诊断和预测河流水环境问题的重要手段[1]. 当前,河流水质模型已被广泛应用于面向流域水环境系统的科学研究、工程规划和管理决策等方面,已成为流域水环境管理不可或缺的手段[2]. 在应用传统的数学模型模拟和预测河流水环境过程时,需要完整的边界条件和初始条件信息以及可靠的模型参数. 然而,由于实际河流的复杂性,开展河流水质模拟分析时常常难以全面收集到河流水质初始条件和边界条件等定解资料. 特别是入河污染负荷,因其由点面源污染综合产生,具有过程复杂、不确定性大等特点,是影响水质模拟精度的重要不确定性源[3]. 当前,我国对于大型工业企业、污水处理厂等大型排口有较好的监测,可较准确地获取其排放过程,但是对于一些小型排口、地表漫流以及地下水渗入等,其入河规模和位置等情况都难以准确估计. 这些缺失的或者具有高度不确定性的污染负荷数据使常规的河流水质模型运行缺少了必要的准确可靠的输入数据,导致常规方法不再有效. 考虑到当前河流关键断面水质浓度有相对完整的观测资料,值得思考如何更好地去利用这些数据,探求河流水质模拟的新方法,为污染负荷缺失条件下河流水质模拟提供新的可能.
基于偏微分方程最优化控制理论的变化同化方法(又称“四维变分同化”,4D-Var)[4]可以通过同化不同类型观测数据,识别模型模拟所需的时空变化参数,改进模型动力过程模拟预测能力. 其在大气科学、海洋科学、水文学和水力学等不同门类学科已有成功的应用[5-9]. 不过,采用变分同化方法开展河流水质模拟的报道仍很少,Cho等[10]在其地表水水质模拟数据同化的回顾论文中提到了2篇利用三维变分同化方法(3D-Var)模拟一维渠道的水质输运过程[11]和水库的水质模拟[12]. 鉴于四维变分同化方法既具备同化观测数据,又可保持物理动力规律约束的能力[13-14],值得加强其在河流水质模拟中的应用研究.
南淝河位于巢湖流域西北部合肥市境内,为城市河流,水环境问题突出. 南淝河是巢湖的主要入湖河流,其水质达标是巢湖流域水污染治理的重点任务[15]. 掌握其水环境变化过程及其入河负荷对水质的影响是开展水环境治理的基础. 但是,与国内城市河流类似,其存在污染来源难以全面排查清楚等问题[16]. 按照常规的传统模型模拟方法,需要提前估算污染入河负荷,才能实现水质过程的模拟. 对于这个入河污染负荷存在很高不确定性的河流,若没有可靠的污染入河数据,将不可能准确模拟其水质动态. 本文以南淝河干流董铺水库以下城区河流水质模拟为例,探究基于变分同化法模拟水质动力过程的性能,为入河污染负荷缺失或具高不确定性条件下河流水质模拟提供可选方法. 研究显示,方法可在提升河流水质模拟精度的同时识别不确知的入河污染负荷,为巢湖流域等环境条件复杂的流域系统中污染定量解析、水质预测预警及污染管控等提供重要支持.
1 研究区域南淝河位于合肥市境内,是巢湖重要的入河支流,也是典型城市河流. 南淝河干流河长约70 km,发源于江淮分水岭大潜山余脉,从西北向东南流入董铺水库、流经合肥市主城区后于入湖口施口处汇入巢湖. 南淝河自董铺水库大坝至入湖口施口全长42.0 km,其间依次有四里河、板桥河、二十埠河、店埠河和长乐河等支流汇入.
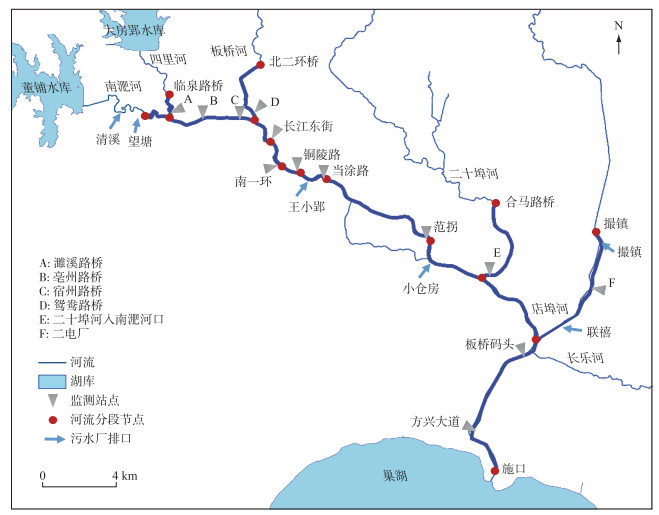
南淝河所在流域多年平均降水量为1022 mm. 尽管降水较为充沛,但是由于上游董铺水库为合肥市的主要饮用水水源,坝下游河段仍缺乏充足的清洁水源补给. 南淝河水源主要为污水处理厂处理后的生产和生活用水的尾水,以及区域内的城市和农村的地表径流等. 受区域密集人口及高速发展的社会经济影响,南淝河水质近年多处于Ⅴ类和劣Ⅴ类水平,水环境问题突出. 目前,干流计算区域内有望塘、清溪、王小郢、小仓房4座污水处理厂尾水入河;店埠河有撮镇和联禧污水处理厂尾水入河(图 1). 其中干流望塘、清溪、王小郢和小仓房污水处理规模总量为110万m3/d. 从2019年运行数据可知,各个污水厂排水基本稳定,达到了准Ⅳ类水质要求.
|
图 1 研究区南淝河水系及关键断面分布 Fig.1 The Nanfei River and the main gauging points |
南淝河水质沿程动态变化过程可采用具有反应源项的一维物质输运方程来表达. 为了简便,仅考虑水体中污染物质沿河纵向的随流输移运动以及沿程的生化降解过程,具体为:
| $ \frac{\partial C}{\partial t}+\frac{\partial}{\partial x}\left(U \cdot C-D \frac{\partial C}{\partial x}\right)=-K \cdot C+S $ | (1) |
式中,C为某水质指标的浓度,mg/L;t为时间,s;D为纵向离散系数,m2/s;U为断面平均流速,m/s;K为某水质指标的一阶衰减系数,s-1;S为某水质指标的外部源汇项,g/(m3 ·s);x为空间坐标.
水质数据同化的目标主要是通过实际观测水质浓度等数据和水质动态模型相互融合以达到提高模型模拟和预测真实物理过程精度. 也就是在水质控制方程约束下,寻找最优的控制变量P(模型初始条件、边界条件和过程参数),使表征模拟结果与观测差异的代价函数J为最小,即:
| $ \begin{aligned} &\min J(P)=\frac{1}{2} \int_{0}^{T}\left\|H \cdot C-C^{\mathrm{obs}}\right\|^{2} \mathrm{~d} t\\ &\left\{\begin{array}{c} F(C, P) \equiv \frac{\partial C}{\partial t}+\frac{\partial}{\partial x}\left(U \cdot C-D \frac{\partial C}{\partial x}\right)-S=0 \\ C(x, 0)=C_{0}, \text { 初始条件 } \\ \left.C\right|_{\partial \Omega}=C_{1}(t), \text { 第一类边界条件 } \\ \left.\frac{\partial C}{\partial x}\right|_{\partial \Omega}=0, \text { 第二类边界条件 } \end{array}\right. \end{aligned} $ | (2) |
式中,T为积分(模拟)时段;H为观测算子;∂Ω表示计算域的边界.
如果能计算出代价函数J关于控制变量P的梯度. 即可用梯度下降类方法求解优化求解代价函数极小值. 变分同化法通过求解伴随方程来快速计算代价函数关于控制变量的梯度[14]. 方程(1)的伴随方程可表达为:
| $ \left\{\begin{array}{c} -\frac{\partial C^{*}}{\partial t}-\frac{\partial U C^{*}}{\partial x}-\frac{\partial}{\partial x}\left(D \frac{\partial C^{*}}{\partial x}\right)+H \cdot C-C^{\mathrm{obs}}+K-\frac{\partial S}{\partial C}=0 \\ C^{*}(T)=0 \\ \left.\frac{\partial C^{*}}{\partial x}\right|_{\partial \Omega}=0 \\ \left.C^{*}\right|_{\partial \Omega}=0 \end{array}\right. $ | (3) |
原方程(1),伴随方程(3)和相应的初始、边界条件构成了双向的积分系统. 其即为一个关于控制变量P的最优化控制系统[17]. 利用最优化算法可实现该最优控制系统的求解,即模拟得到与观测资料最为接近的水质过程. 基于该最优化系统建立的模型即为水质变分同化模型. 本文建模采用了适用于大规模问题计算的拟牛顿算法L-BFGS[18]作为最优化算法,同化模型整体架构可参考文献[17],这里不再赘述. 模型采用Fortran语言编码.
2.2 南淝河模型构建根据南淝河的实际可用资料情况,模型计算范围设定为董铺水库以下5.3 km至入湖口施口(图 1),模拟干流段总长34.2 km. 具体包括南淝河干流(从望塘污水厂下游监测站开始至施口断面止)、四里河入河口段(临泉路)、板桥河入河口段(北二环路桥)、二十埠河入河段(合马路)、店埠河入口段(撮镇). 河道模拟计算分为14个河段,干流内部的分段节点分别为四里河入河口、板桥河入河口、长江东街、南一环、铜陵路、当涂路、范拐、二十埠河入口以及店埠河入口. 各河段又划分成计算断面,各断面间距根据河道形态取800~1200 m不等.
南淝河的水质计算边界主要包括干支流入流的水质浓度过程(第一类边界条件)、南淝河入湖口的自由输出边界条件(第二类边界条件)以及侧向污水处理厂和长乐河等支流的入流负荷边界条件. 入流浓度过程包括干流上游、四里河临泉路、板桥河北二环路桥、二十埠河合马路和店埠河撮镇共5个边界水质指标浓度过程.
入河负荷是水质计算的主要影响要素. 南淝河污染包括污水处理厂等排口以及地表漫流. 已知的污水厂排口数据作为点源考虑,包括计算区域内直接汇入干流的清溪、望塘、王小郢、小仓房以及汇入店埠河的联熹和撮镇污水处理厂尾水. 对于一些小型排口及地表漫流,其入河负荷情况难以掌握. 在本次计算中将这些未知污染负荷计入非点源处理,作为模型的控制变量,通过变分同化模型进行识别计算,解决了传统模型若数据缺失则难以可靠模拟的问题.
模型的其他计算参数,如河流非恒定的水动力参数由水动力模型计算提供;本次计算氨氮和总磷一阶衰减系数[19]分别取0.06和0.04 d-1.
2.3 数据选用本文以氨氮和总磷作为代表性水质指标,模拟时段为2019年10-12月. 南淝河水质模拟的边界条件和初始条件等数据根据自动监测站采集的逐日平均氨氮和总磷数据给定. 污水处理厂尾水排放数据也基于逐日监测的过程数据. 模型同化观测资料来自于南淝河干流自动监测站,本次选用了方兴大道、板桥码头、范拐、当涂路、铜陵路、南一环、长江东街、宿州路桥、亳州路桥、四里河濉溪路桥、板桥河鸳鸯路桥、二十埠河入南淝河口、店埠河二电厂(图 1)等站的自动监测数据,时间频次为d.
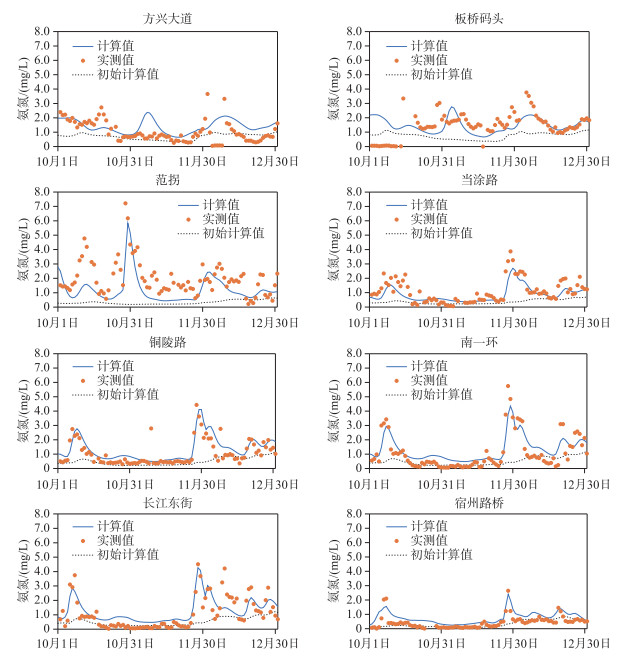
3 结果分析与讨论 3.1 模拟结果采用模型分别计算了分散点源和面源入河污染负荷数据缺失条件下南淝河水质过程,以及将这些非点源负荷作为控制变量模拟的结果. 由于实际问题非线性强,迭代收敛性能受制约,本次南淝河模拟经过5000次迭代,代价函数相对值从1降低至0.416,降幅为59.4 %. 以此结果作为采用变分法得到的计算成果进行了分析. 图 2和图 3展示了分散点源和面源入河污染负荷数据缺失条件下初始计算结果和采用变分法计算结果与实际过程的比较.
|
图 2 变分同化前后各站点氨氮过程线与实测值的比较 Fig.2 Comparison of measured ammonia nitrogen concentration hydrograph with the modeled ones before and after variational assimilation |

|
图 3 变分同化前后各站点总磷过程线与实测值的比较 Fig.3 Comparison of measured total phorsphorus concentration hydrograph with the modeled ones before and after variational assimilation |
从各监测断面水质过程来看,若分散点源以及面源的入河数据缺失,计算得到各断面水质过程在长期无降雨时段(11月),当涂路以上站点的水质过程相对比较一致. 不过,下游段,特别是板桥码头和范拐断面的计算值较实测值偏低,说明在该河段内旱季也有污染汇入;而方兴大道低估又有减少,这可能和南淝河会出现水流倒灌入河的情况有关. 在降雨影响的时段,计算结果偏差较大. 统计表明(表 1),各断面模拟结果的均方根误差(RMSE)明显偏大,纳什效率系数(NSE)除个别断面个别指标外,多数小于0. 这也说明,南淝河水质模拟仅考虑污水处理厂等尾水排放还不够. 受降雨影响的时段,南淝河沿程仍有大量雨污水汇入南淝河,造成南淝河的污染物浓度升高,水质变差,需对这些分散式的污染负荷加以考虑.
| 表 1 变分同化前后各站点氨氮和总磷模拟计算精度比较 Tab. 1 Modeling accuracy of ammonia nitrogen and total phosphorus before and after assimilation |
采用变分法同化观测数据后,模拟得到的各断面水质过程计算结果得以大幅校正,捕捉到了各个污染指标波动的峰值,较好地模拟了南淝河实际的水质变化过程. 虽然存在计算偏高和偏低等问题,特别是范拐断面的氨氮模拟结果偏低较为明显,可能由于实际问题的复杂性限制,使模型并没有收敛到理想状态. 但是,从总体来看,计算结果均方根误差有明显下降. 氨氮RMSE从各断面平均的1.03 mg/L降至0.69 mg/L,NSE则从平均-0.66上升到0.16. 总磷RMSE从各断面平均的0.07 mg/L降至0.06 mg/L,NSE则从平均-1.50上升到-0.21. 从各断面的各自变化来看,干流长江东街到当涂路河段的水质模拟精度改进更为明显. 氨氮和总磷的NSE均从小于0分别提高至0.62和0.50. 下游施口、方兴大道等断面模拟精度较差,可能与巢湖水体出现倒流等因素有关.
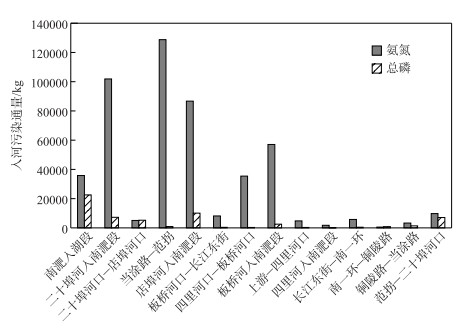
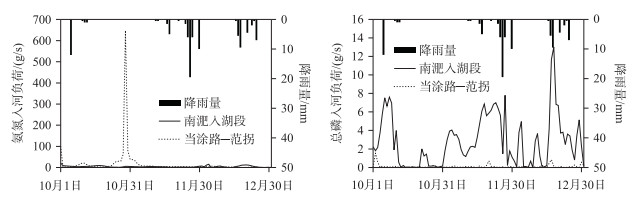
3.2 负荷识别结果本次模拟以入河非点源负荷作为控制变量, 采用变分同化模型模拟得到南淝河水质过程的同时, 也识别得到了南淝河的入河非点源负荷过程. 各河段在模拟时段内(10-12月)入河负荷总通量如图 4所示. 南淝河沿程各河段均有污染输入. 其中,氨氮负荷在当涂路-范拐河段、二十埠河入南淝河段、四里河口-板桥河口河段、板桥河入南淝河河段以及南淝河入湖段均较高;总磷负荷较高的河段则为南淝河入湖段、二十埠河入南肥河段以及店埠河入南肥河段等. 通过同化不仅可得到各河段的负荷总通量数据,而且直接得到了入河污染负荷通量随时间的变化过程. 这里选择南淝河入湖段以及当涂路-范拐河段的入河过程为例加以说明模型的性能. 从图 5中可以看出,污染负荷随降雨过程的变化比较明显,对应10月5日、11月24-30日以及12月16-25日每场降雨,各河段的氮、磷均可形成不同量级的负荷峰值. 说明降雨引起的雨污溢流问题对南淝河水质有重要影响. 此外,本次计算还识别出了当涂路-范拐段河段10月末存在一个很高的氨氮入河峰值,为647.45 g/s. 虽然该负荷未知来源,但是根据范拐及板桥码头断面在10月底出现的氨氮浓度峰值,可以确认这是合理的. 这也从侧面说明了该模型对未知的污染来源有很强的识别能力,可在今后应用于河流污染来源的定量追溯分析. 对于巢湖等流域入湖污染控制与河流水质预测预警具有重要价值.
|
图 4 南淝河各河段识别的污染负荷 Fig.4 Identified pollutant loads in each reach of the Nanfei River |
|
图 5 南淝河入湖段及当涂路-范拐河段的入河负荷过程 Fig.5 Hydrograph of pollutant loads in the two typical reaches and the corresponding rainfall during this period |
以巢湖流域南淝河干流为研究对象,基于变分同化方法构建了南淝河水质模型,模拟了2019年10-12月间南淝河干流及支流入河段的水质时空动态变化. 与实际观测数据以及基于已知污染负荷数据代入常规模型模拟结果的对比分析表明:
1) 基于变分同化方法建立的南淝河水质模型可模拟入河污染负荷数据缺失条件下南淝河水质过程,成功捕捉水质波动变化的不同峰值,水质浓度模拟精度明显改进. 该方法为缺资料地区河流模拟提供了可能的手段.
2) 模型在计算水质过程的同时,也得到了南淝河各河段的入河负荷动态变化过程,为河流水质污染溯源及成因分析提供了定量数据支持. 模拟结果表明,本文提出的方法对入河污染敏感,可用于关键河段污染定量溯源,可支撑巢湖等流域复杂河流的入湖污染控制.
3) 基于变分同化法的水质模拟通过同化河道内水质指标浓度观测数据,代替常规模型需要以入河污染负荷数据作为输入条件的应用前提. 亦即以河道内的浓度观测数据作为输入条件代替污染入河负荷作为输入条件,避开了入河负荷准确估算的难点,使得在复杂环境条件下河流水质模拟更为可靠. 南淝河的水质模拟研究展现了该模型在复杂环境条件下的应用潜力,对流域河流水质预测预警及污染管控具有重要意义.
| [1] |
EPA. Guidance on the development, evaluation, and application of environmental models. US Environmental Protection Agency, 2009. EPA/100/K-09/003.
|
| [2] |
Lai XJ. A review of integrated water quality modeling for a watershed. Progress in Geography, 2019, 38(8): 1123-1135. [赖锡军. 流域水环境过程综合模拟研究进展. 地理科学进展, 2019, 38(8): 1123-1135.] |
| [3] |
Loucks DP, van Beek E. Water quality modeling and prediction. In: Loucks DP, van Beek E eds. Water resource systems planning and management: An introduction to methods, models, and applications. Cham: Springer International Publishing, 2017: 417-467.
|
| [4] |
Zou XL. Four-dimensional variational data assimilation. Atmospheric Satellite Observations. Amsterdam: Elsevier, 2020, 163-174. DOI:10.1016/b978-0-12-820950-9.00009-x |
| [5] |
Fletcher SJ. Applications of data assimilation in the geosciences. Data Assimilation for the Geosciences. Amsterdam: Elsevier, 2017, 887-916. DOI:10.1016/b978-0-12-804444-5.00023-4 |
| [6] |
Janeković I, Mihanović H, Vilibić I et al. Using multi-platform 4D-Var data assimilation to improve modeling of Adriatic Sea dynamics. Ocean Modelling, 2020, 146: 101538. DOI:10.1016/j.ocemod.2019.101538 |
| [7] |
Ghorbanidehno H, Kokkinaki A, Lee J et al. Recent developments in fast and scalable inverse modeling and data assimilation methods in hydrology. Journal of Hydrology, 2020, 591: 125266. DOI:10.1016/j.jhydrol.2020.125266 |
| [8] |
Honnorat M, Monnier J, Dimet FX. Lagrangian data assimilation for river hydraulics simulations. Computing and Visualization in Science, 2009, 12(5): 235-246. DOI:10.1007/s00791-008-0089-x |
| [9] |
Lai X, Liang Q, Yesou H et al. Variational assimilation of remotely sensed flood extents using a 2-D flood model. Hydrology and Earth System Sciences, 2014, 18(11): 4325-4339. DOI:10.5194/hess-18-4325-2014 |
| [10] |
Cho KH, Pachepsky Y, Ligaray M et al. Data assimilation in surface water quality modeling: A review. Water Research, 2020, 186: 116307. DOI:10.1016/j.watres.2020.116307 |
| [11] |
Shao DG, Wang ZM, Wang B et al. A water quality model with three dimensional variational data assimilation for contaminant transport. Water Resources Management, 2016, 30(13): 4501-4512. DOI:10.1007/s11269-016-1432-5 |
| [12] |
Babbar-Sebens M, Li L, Song K et al. On the use of Landsat-5 TM satellite for assimilating water temperature observations in 3D hydrodynamic model of small inland reservoir in Midwestern US. Advances in Remote Sensing, 2013, 2: 214-227. DOI:10.4236/ars.2013.23024 |
| [13] |
Lawless AS. Variational data assimilation for very large environmental problems. Large Scale Inverse Problems: Computational Methods and Applications in the Earth Sciences, 2013, 13: 55-90. |
| [14] |
LeDimet FX, Talagrand O. Variational algorithms for analysis and assimilation of meteorological observations: Theoretical aspects. Tellus A: Dynamic Meteorology and Oceanography, 1986, 38(2): 97-110. DOI:10.3402/tellusa.v38i2.11706 |
| [15] |
Zhang M, Kong FX. The process, spatial and temporal distributions and mitigation strategies of the eutrophication of Lake Chaohu (1984-2013). J Lake Sci, 2015, 27(5): 791-798. [张民, 孔繁翔. 巢湖富营养化的历程、空间分布与治理策略(1984-2013年). 湖泊科学, 2015, 27(5): 791-798. DOI:10.18307/2015.0505] |
| [16] |
Zhang D, Tian X, Wu S. Analysis of pollution flux in Nanfeihe River and its treatment. Water Resources Protection, 2020, 1-6. [张笛, 田鑫, 吴师. 南淝河污染通量解析与治理. 水资源保护, 2020, 1-6.] |
| [17] |
Lai XJ, Fu GS, Sun B. Optimal control problems in unsteady flow computation and their variational solutions. Advances in Water Science, 2008, 19(4): 537-545. [赖锡军, 傅国圣, 孙波. 非恒定水流计算的最优控制问题及其变分求解. 水科学进展, 2008, 19(4): 537-545. DOI:10.3321/j.issn:1001-6791.2008.04.014] |
| [18] |
Gilbert JC, Lemaréchal C. Some numerical experiments with variable-storage quasi-Newton algorithms. Mathematical Programming, 1989, 45(1/2/3): 407-435. DOI:10.1007/BF01589113 |
| [19] |
Feng S, Li XY, Deng JC. Determination of comprehensive pollutants attenuation coefficients of the plain river networks in the upper reaches of Lake Taihu Basin. Acta Scientiae Circumstantiae, 2017, 37(3): 878-887. [冯帅, 李叙勇, 邓建才. 太湖流域上游平原河网污染物综合衰减系数的测定. 环境科学学报, 2017, 37(3): 878-887. DOI:10.13671/j.hjkxxb.2016.0125] |
 2021, Vol. 33
2021, Vol. 33 

