(2: 河海大学水文水资源学院, 南京 210098)
(3: 河海大学水利水电学院, 南京 210098)
(2: College of Hydrology and Water Resources, Hohai University, Nanjing 210098, P. R. China)
(3: College of Water Conservancy and Hydropower, Hohai University, Nanjing 210098, P. R. China)
水库是在降雨时空分布不均匀地区,缓解防洪与兴利矛盾,保障防洪、供水和生态安全的重要工程措施[1-2]. 截至2018年底,我国已建成98822座水库,总库容9707亿m3,仅大中型水库近4690座,总库容超过8243亿m3[3]. 可以说,在我国已经几乎不存在完全意义上的天然流域了. 近年来,气候变化和人类活动加剧,流域水文情势发生了较大变化,很多水库(湖泊)其入库洪水序列已经不再满足水文一致性假设[4-5]. 设计洪水、水库设计及运行调度的原有计算方法面临严峻挑战[6-7],据此给出的水库调度方案,或因高估设计洪水导致水库功能发挥不充分,或因低估设计洪水增大水库安全风险. 因此,在诊断水文非一致特性的基础上,对水文序列进行一致性处理,并建立适应非一致性条件、充分发挥水库设计效益的调度方法,是当前亟待解决的重要研究课题.
自2008年Milly等[8]在Science上发表论文“Climate change. Stationarity is dead: whither water management?”以来,有关水文非一致性诊断方面的研究引起了国内外学者的广泛关注. 先后提出了多种检验方法,主要有Mann-Kendall、Spearman秩次相关检验法和贝叶斯方法等[9-10]. 由于单一检验方法存在不稳定性,2010年谢平等[11]提出了融合多种方法的水文变异诊断系统,应用结果表明与单一诊断方法相比,综合诊断系统结果更加可靠,现已成为趋势性和跳跃性分析的常用方法. 对已发生变异的水文序列进行还原或还现,再对其进行频率分析是非一致分布水文序列频率分析的重要内容[12-13]. 目前,还原或还现的方法主要包括:变异点前后序列与某一参数的关系分析法、时间序列的分解与合成方法和水文模型方法[7]. 其中,水文模型法利用模型参数的变化反映流域下垫面变化带来的影响,通过不同时期的降雨资料与某一时期(变异点前或后)的参数结合,实现水文序列的还原与还现[7, 14]. 由于该方法具有一定的物理意义和较强的解释能力,是目前较为常用的方法. 王国庆等[14]以黄河中游三川河流域为例,采用流域水文模型模拟了1970s后的天然径流过程,定量评估了气候变化/人类活动对流域径流的影响. 王忠静等[15]针对变化环境条件下水资源评价中的“还原失真”和“还原失效”问题,基于分布式水文模型提出了变化环境下水资源评价新方法. 韩瑞光等[16]应用河北雨洪模型对阜平站1980s前后的洪水序列进行了研究,把洪水序列统一修正到1980s后下垫面条件下的洪水序列. 环境变化下如何更好地对水库进行适应性调度受到国内外学者的广泛关注[17-18]. 张玮等[19]针对气候变化对水库调度带来的不利影响,提出一种基于DS理论的水库适应性调度规则. 吴书悦等[20]评估了气候变化对径流和新安江水库调度的影响,并结合气候模型与新安江模型绘制了水库适应性调度图. 为在一定约束条件下,实现水库防洪与兴利效益最大化,学者们提出了多个数学规划和启发式算法[21]. 数学规划方法一般有严密的数学理论支撑,具有收敛速度快、约束条件明确的优点,虽在计算效率和灵活性上有时不如启发式算法,但在目标函数和水库数量较少的情况下优势明显. 其中,动态规划(dynamic programing,DP)在利用递归公式逐时段寻优的同时,保证了全局最优性,是水库优化调度的常用方法,应用广泛[22-23].
综上所述,国内外学者分别在水文非一致性诊断、一致性处理与水库适应性调度等方面开展了系列研究,取得了丰富的研究成果,但鲜见适应非一致性条件的水库优化调度方法体系. 为此,本文建立集水文非一致性诊断、水文模型还现、设计洪水计算与面向防洪安全的水库调度规则优化于一体的水库适应性调控方法体系,并在沭河流域仕阳水库开展应用研究,旨在定量解析人类活动对流域洪水影响程度的基础上,通过优化流域内现有水利工程的调度方式,降低环境变化对入库洪水改变带来的不利影响,提出现状条件下最大化防洪效益的水库调度方案,保障水库预期效益的发挥.
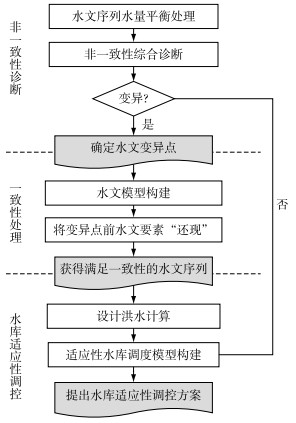
1 适应水文非一致条件的水库优化调度方法适应水文非一致条件的水库优化调度方法体系(图 1)主要包括:(1)水文非一致性诊断. 目的是判断水文序列是否存在非一致性变化,特别是变异特性,并确定变异点;(2)水文一致性处理. 对于确定存在变异特性的水文序列,利用水文模型进行还现,得到满足一致性的水文序列;然后进行频率分析,计算满足一致性的水库设计洪水;(3)水库调度方案优化. 建立最大化防洪效益的水库优化调度模型,通过模型求解得到变化条件下水库适应性调度方案.
|
图 1 适应非一致性条件的水库优化调度技术框架 Fig.1 Technical framework for optimal reservoir operation under non-stationary conditions |
(1) 水文序列变异诊断:水文序列一致性审查是工程设计的前提[24]. 首先采用线性滑动平均法、Hurst系数法及累积模比系数法对水文序列进行初步诊断,判断其序列是否可能存在变异;如发生变异,就要进一步诊断和分析突变性和趋势性. 借鉴综合诊断法[11],本研究中采用的趋势性诊断方法包括非参数Speraman秩次相关检验法和线性趋势相关系数;变异诊断方法包括采用Mann-Kendall(M-K)检验法、有序聚类检验法、Lee-Heghinian检验法、滑动T检验法、滑动秩和检验法及MWP检验法. 通过上述非参数统计方法获得数值分析结果后,根据需要再结合物理成因,确定最可能的变异点.
(2) 水文序列一致性处理及设计洪水推求:对于诊断出具有非一致性的水文序列,首先利用水文模型方法进行还现,获得满足一致性的水文序列,然后进行频率分析. 主要步骤是:首先建立符合现状下垫面条件(变异点后)的水文模型;然后将不同时期降雨、蒸发等资料,输入具有良好精度的水文模型,计算得到现条件下满足一致性要求的径流过程,并根据需要遴选水文特征序列,例如洪峰、时段洪量;最后采用P-Ⅲ概率分布对还现后的特征序列进行频率分析,进而基于同频率放大法对水库入库典型洪水过程进行放大,得到不同频率的设计洪水过程线.
(3) 最大化防洪效益的水库优化调度模型:水文序列一致性条件发生改变,直接影响设计洪水成果的大小,从而影响水库预期功能的发挥. 若变异后设计洪水变小,即相当于水库工程原设计时高估了设计洪水,则会导致水库功能发挥不充分;反之,若变异后设计洪水变大,导致水库规模一定条件下,水库运行安全风险加大. 但无论如何变化,对于建成后的水库而言,最有效的办法是完善水库调度方案,实现水库预期功能最大化. 对于前一种情况,通过抬升退水期的运行水位,适量增加水库蓄量,一方面能减轻下游河道或者水库的防洪压力;另一方面由于水库防洪库容偏大,也能保障水库自身安全. 对于第二种情况,则需要在洪水起涨前,适当降低水库的运行水位,为超过原设计的洪水腾空更多的防洪库容. 为此,本研究构建了以防洪效益最大化(水库最高水位最小)为目标的水库优化调度模型.
目标函数:
| $ F = {\rm{min}}\left( {Z_{{\rm{max}}}^t} \right), t = 1, 2, \ldots , n $ | (1) |
式中,F为目标函数,Zmaxt为调度过程中水库最高水位,n为调度过程总时段数.
约束条件:
1) 水量平衡方程约束:
| $ {V_{t + 1}} = \left( {{I_t} - {Q_t}} \right)\Delta t + {V_t} $ | (2) |
式中,Vt、Vt+1为t时段初、时段末水库蓄水量,It为t时段水库的平均入库流量,Qt为水库t时段平均下泄流量,Δt为时间长.
2) 水库水位约束:
| $ {Z_{{\rm{min}}}} \le {Z_t} \le {Z_{{\rm{max}}}} $ | (3) |
式中,Zmin为水库调度过程中允许最低水位;Zt为t时刻初水库水位,Zmax为水库允许最高水位,不同频率洪水Zmax取值可能不同.
3) 水库下泄能力约束:
| $ {Q_t} \le {Q_{{\rm{max}}}} $ | (4) |
式中,Qt为时段t出库平均下泄流量;Qmax为最大下泄流量.
4) 水库下游防洪安全约束:
| $ {Q_{{\rm{max}}}} = {\rm{min}}\left( {{Q_{{\rm{an}}}}, Q\left( z \right)} \right) $ | (5) |
式中,Qan为水库下游河道安全下泄流量,Q(z)为库水位为z时的下泄能力. 防洪调度工作中,大坝安全是最为关键的工作,因此要在保证大坝安全的基础上,尽量在下游安全下泄流量范围内泄洪.
模型求解:对于单个水库,建议采用经典动态规划方法进行求解,随着状态空间逐步加密,可逼近全局最优解;若是含有多个水库的水库群系统,建议采用离散微分动态规划算法(discrete differential dynamic programming,DDDP)进行求解,DDDP有效解决了计算效率与精度的统一问题.
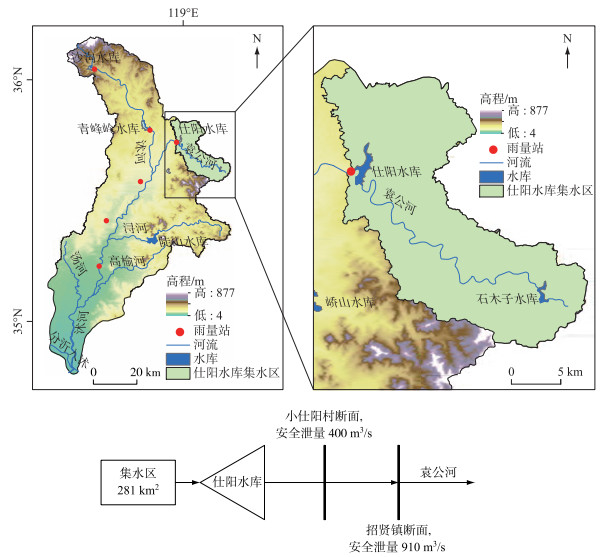
2 应用实例 2.1 研究区概况与数据仕阳水库位于沂沭泗流域中的沭河流域,控制流域面积281 km2,总库容1.25亿m3,兴利库容0.69亿m3,是一座具有多年调节能力的大型水利枢纽,以防洪、灌溉为主,兼顾发电与养鱼. 水库2010年经除险加固后,满足100年一遇洪水设计、5000年一遇洪水校核要求. 仕阳水库保护下游1.63万hm2耕地和30万人口,还有206国道、335省道、日东高速公路、胶新铁路等重要交通设施. 下游小仕阳村处河道安全下泄流量为400 m3/s,招贤镇断面河道安全行洪流量为910 m3/s(图 2). 仕阳水库汛限水位为153.00 m,设计洪水位为155.55 m,校核洪水位为158.11 m. 水库现状防洪调度规则为:遭遇20年一遇设计洪水,153.00 m起调,控泄400 m3/s,保护小仕阳村,计算最高雍水位为155.00 m;100年一遇设计洪水,153.0 m起调,水位上涨到155.0 m前控泄400 m3/s,155.0 m后敞泄,计算最高雍水位为155.33 m. 此外,本研究还收集了1961—2013年间水库入库洪水和库区逐小时降雨等资料. 并对入库洪水年最大洪峰流量序列、年最大24 h洪量序列与年最大72 h洪量序列进行初步分析,3个序列存在增大趋势,尤其是年最大洪峰增加趋势较为明显.
|
图 2 研究区域地图及概化图 Fig.2 Study area map and engineering generalization map |
经M-K等方法诊断仕阳水库1961—2013年实测入库洪水年最大洪峰流量序列、年最大24 h洪量序列与年最大72 h洪量序列. 如表 1所示,各序列变异点大致有1965、1975、1976、1998、1999、2000和2001年7个变异点,其中1976年是1975年的延迟变异点,1999—2001年是1998年的延迟变异点,故上述序列存在1965、1975和1998年3个可能变异点.
| 表 1 各洪水序列变异诊断结果 Tab. 1 Diagnosis results of variation of flood time series |
为了从上述3个变异点中识别最可能变异点,从气候变化和人类活动角度开展了如下分析:(1)仕阳水库实测洪水序列年限为1961—2013年,故从统计角度而言,靠近序列首端的1965年作为变异点不太可靠. (2)借助降雨量分析,由于遭遇“1997 ·8”暴雨,故诊断出的1998年延迟变异点不能认为是由于流域下垫面变化导致的变异点,而归结于气候所导致的变异点又过于片面,还需针对长系列水文气象资料进一步分析确认,多种诊断方法中1998年出现的次数很少,暂不考虑这个变异点. 年最大洪峰序列分析中,取置信度水平为0.05时,有序聚类、Lee-Heghinian、滑动T检验的值都在1975年达到了最大,为4.68;年最大24 h洪量检验中,有序聚类、Lee-Heghinian、滑动T检验的值都在1975年达到了最大,为3.45,滑动秩和检验和MWP分析检验值同样最大,分别为2.8和0.04,均为显著跳跃;年最大72 h洪量检验结果与最大72 h洪量检验结果类似. 综合各诊断方法的诊断结论,仕阳水库年最大洪峰序列、年最大24 h洪量序列、年最大72 h洪量序列的变异点确定为1975年.
2.2.2 一致性处理首先利用新安江模型构建了仕阳水库流域水文模型,然后在变异点(1975年)处将降雨序列分为两个子序列,利用变异点后(1975—2013年)的序列进行水文模型参数率定,得到反映现状下垫面特性的模型参数,结果见表 2.
| 表 2 新安江模型率定参数 Tab. 2 The calibrated parameters of Xin'anjiang model |
将变异点前降雨资料输入到率定好的模型中,模拟历史降雨在现状下垫面条件下的产汇流过程,得到还现后的入库洪水过程. 从洪水过程中提取出年最大洪峰、年最大24 h洪量、年最大72 h洪量序列值,与变异后子序列值相结合,得到满足一致性要求的新序列. 同时,作为对比,笔者也计算了实测(忽视水文序列非一致性)入库洪水的年最大洪峰、年最大24 h洪量、年最大72 h洪量序列. 在此基础上,利用P-Ⅲ分布对两组序列进行了频率分析,不同序列统计参数见表 3.
| 表 3 仕阳水库各变异洪水序列的参数估计结果 Tab. 3 Parameter estimation results of non-stationary flood series of Shiyang Reservoir |
由表 3可知,水文序列一致性处理后的新序列,较之原序列统计参数发生了一定程度的改变,特别是均值增大较为明显,年最大洪峰、年最大24 h洪量、年最大72 h洪量分别增大了19.7 %、14.5 % 和10.0 %. 主要受以下3个方面影响:1)区域城镇化水平提升导致流域不透水面积增大,产流比例和汇流速度增加[25];2)堤防标准提升与河道整治引起洪水归槽效应[26];3)气候变化影响. 相关研究成果[27]同样表明淮河流域大部分气象站点降雨量无明显变化趋势,气候变化对淮河流域洪水影响不大.
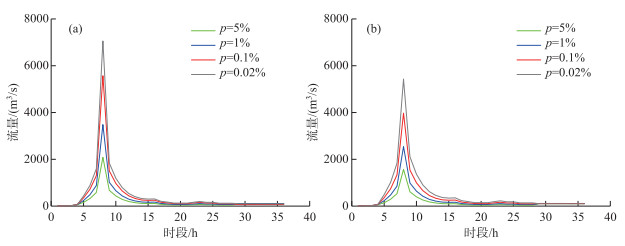
在变异点后,发生在1998年7月的洪水为仕阳水库建库以来规模最大的洪水,本文以此作为典型洪水进行同频率放大,从而获得了不同频率(p)下的设计洪水过程线. 基于一致性处理序列和实测洪水序列得到设计洪水过程线(图 3),从中可以看出,考虑一致性影响后,仕阳水库设计洪水明显增大,特别是洪峰,5000年一遇、1000年一遇、100年一遇和20年一遇设计洪水洪峰分别增加了2065、1595、942和512 m3/s. 如根据原有设计洪水来制定水库防洪调度规则,将显著增加水库和下游河道的防洪风险,特别是在流域遭遇百年及特大洪水时.
|
图 3 仕阳水库入库洪水设计洪水过程线:(a)满足一致性要求序列;(b)实测序列 Fig.3 Design flood hydrographs of Shiyang Reservoir: (a) the stationary series; (b) the observed series |
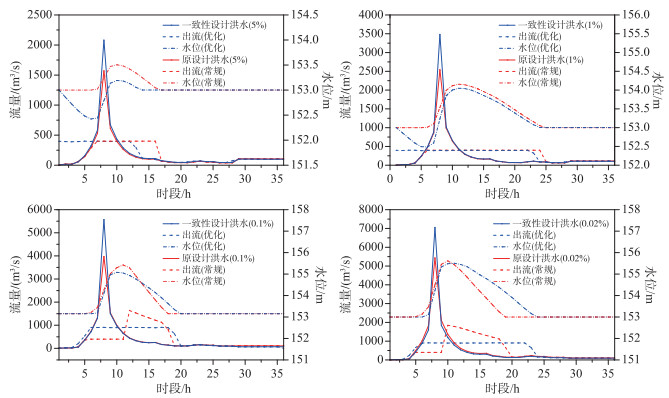
为与适应性调度进行对比,首先利用现状水库调度规则对原设计洪水进行了调度,不同量级设计洪水调度过程见图 4中红色线条. 20年一遇、100年、1000年一遇和5000年一遇设计洪水下,水库的最高水位分别达到了153.51、154.16、154.98和155.62 m;最大下泄流量分别为400、400、1639和1843 m3/s.
|
图 4 仕阳水库适应性调度过程与原调度过程的对比 Fig.4 Comparison between adaptive operation process and original operation process of Shiyang Reservoir |
依据第1节提出的水库优化调度模型构建了仕阳水库防洪调度模型,模型的输入为一致性条件下的设计洪水. 为适应变化环境导致的设计洪水的峰和量显著增大,在优化模型的约束条件中:对于设计标准内的20年一遇和100年一遇洪水,其最高水位Zmax分别为153.51和154.16 m,最大下泄流量Qmax为400 m3/s,即要求水库在还现后的设计洪水下最大水位和最大下泄流量不超过原设计值;对于超标准的1000年一遇和5000年一遇洪水,其最高洪水位也不超过现状值(154.98和155.62 m),最大下泄流量Qan为招贤镇断面河道安全行洪流量,910 m3/s. 模型构建完成,采用动态规划方法进行求解,调度结果见图 4.
从调度结果可以看出,通过适应性调度,水库最高水位和最大下泄流量均未超过原设计洪水在现行调度规则下的相应值. 其中,水库最高水位下降量在0.11~0.32 m之间,20年一遇设计洪水情景水位下降最为明显(表 4);水库最大下泄流量在设计标准内洪水情景下均未超过原设计值,能满足保护下游小仕阳村的要求,且在超标准洪水情况下,通过限制最大下泄洪水流量不超过910 m3/s,全程未出现敞泄情况,较现状调度规则,更好地实现了对下游招贤镇的保护.
| 表 4 调度过程特征量对比 Tab. 4 Comparison of characteristic quantities in operation process |
上述结果可以看出,本文提出的适应水文非一致条件的水库优化调度方法,能够很好地适应水文序列变异导致设计洪水变化,有利于发挥水库预期功能,降低由水文变异增加的防洪风险.
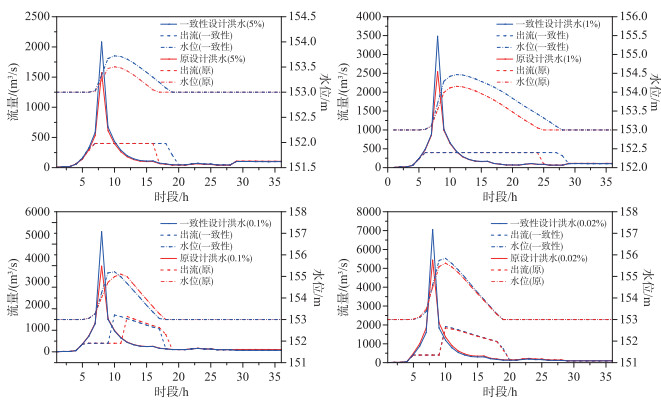
2.3 讨论为分析水文非一致性对水库防洪安全的影响,基于仕阳水库现行调度方式,分别对上述不考虑变异和考虑变异两种入库设计洪水进行了调度. 由图 5可以看出,如不改变水库调度方式,水文变异导致的设计洪水增大,显著抬升水库最高壅水位,特别是对防洪标准内的洪水. 其中20年和100年一遇设计洪水下,水库最高水位分别增加了0.21和0.31 m(表 5). 此外,虽然水库最大下泄流量没有增加,但泄洪时长均显著增加. 事实上,这些出现概率相对较大的洪水,如本例中的20年一遇和100年一遇洪水更容易造成洪水灾害,是流域防御的重点对象[28-29]. 因此,针对水文变异导致的防洪风险增加,水库有必要进行对应的改变. 本文提出适应性调度方法的基本思想是,变异后的设计洪水经过优化调度后水库的最高洪水位与最大下泄流量均不超过现状调度下的特征值. 然而,对于大多数水库,特别是单库,现行的削峰调度规则对于防洪来说已然是非常优秀的调度规则,其优化空间很小[30-31]. 从图 4中水位过程线可以看出,为实现洪水适应性调度的目的,优化模型实质上是通过在洪峰到来前进行预泄,腾空了部分库容. 可以预见的是,若不进行预泄,现状条件下由于洪水量级变化某些水库可能会出现调洪最高水位高于常规调度的最高水位,这更突显了进行适应性调度研究的重要性. 此外,通过优化调度得到的解最优解是水库实际调度能够达到的上限,预报调度只有在预见期足够长、预报精度非常高的情况下才能接近该效果.
|
图 5 考虑非一致性的设计洪水与原设计洪水在现状调度规则下的调度过程 Fig.5 The operation process of consider non-stationary design flood and original design flood under current operation rules |
| 表 5 现行调度规则下水库运行结果 Tab. 5 Reservoir operation results under the current operation rules |
对于设计标准外的稀遇洪水,即使水文变异增大了设计洪水的洪峰与洪量,但由于原设计洪水已经很大,即使调度规则不改变,水库最高水位变化也不明显,本例中1000年一遇和5000年一遇分别增大了0.06和0.22 m. 1000年一遇洪水下最高洪水位虽然变化不大,但洪水下泄提前,持续时间增长;而5000年一遇设计洪水下,洪水下泄过程几乎相同,说明常规调度规则已没有进一步调节洪水的能力. 本文提出适应性调度方法的结果表明,在超标准洪水下,仕阳水库仍能以控泄形式对洪水进行调节,实现保护水库自身和下游保护目的.
从仕阳水库的运用结果来看,本文提出的非一致性条件下水库适应性调度方法相较于水库现行调度技术能够更加充分地发挥水库预期功能. 在实际运用中,对于入库洪水序列不满足一致性假设的水库,根据本文提出的方法计算得到现状条件下设计洪水,然后与原设计洪水比较,当设计洪水确有改变时应重新制定水库调度规则. 当设计洪水增大时,可在现状调度规则的基础上,降低水库的起调水位,来确保水库安全;当设计洪水变小时,可在现行调度规则的基础上,适当减小最大下泄流流量以减小下游防洪压力,或者增加水库蓄量,更好地发挥水库兴利效益. 由于不同水库的工程调控能力和现行调度规则不同,在运用本文所提出的方法时,适应性调度规则的提出需要决策者通过优化或者多方案比较来最终确定. 相关研究[27]指出未来气候变化可能导致淮河流域中小洪水(5~20年一遇)的洪量设计值较历史时期增大. 因此,结合气候模式与本文提出的适应性调控技术框架,预测未来降雨变化,研究未来情景下的水库防洪调度方案是保障仕阳及类似水库防洪安全的可行措施之一.
3 结论受气候变化和人类活动的强烈影响,绝大部分水库入库洪水序列不再满足一致性假设,继续采用水库设计时形成的调度规则,往往难以充分发挥水库设计功能与效益,甚至可能带来防洪或供水风险. 为此,本文提出了水文非一致性诊断→水文模型还现→设计洪水计算→面向防洪安全的水库优化调度于一体的水库适应性调控方法体系,并将其运用于仕阳水库. 取得的主要结论有:
1) 仕阳水库年最大洪峰序列、年最大24 h洪量序列、年最大72 h洪量序列的变异点均为1975年. 考虑一致性影响后,仕阳水库设计洪水明显增大,特别是洪峰,5000年一遇、1000年一遇、100年一遇和20年一遇设计洪水洪峰分别增加了2065、1595、942和512 m3/s.
2) 如继续采用水库原调度方式,水文变异导致的设计洪水增大,将显著抬升水库最高壅水位,特别是对防洪标准内的洪水. 其中,20年和100年一遇设计洪水下,仕阳水库最高水位分别增加了0.21和0.31 m.
3) 针对满足一致性要求的设计洪水,通过优化调度,水库最高水位下降量在0.11~0.32 m之间,20年一遇设计洪水情景水位下降最为明显;水库最大下泄流量均未超过原设计值,能满足保护下游小仕阳村的要求,且在超标准洪水情况下,全程未出现敞泄情况,较现状调度规则,更好地实现了对下游的防洪.
本研究中仕阳水库属于水文变异导致设计洪水增大、防洪风险增大的案例,适应性调度的主要目的是降低由水文变异增加的防洪风险,这对于防洪为主的流域具有很好的借鉴意义. 可以预见的是,对于水文序列具有明显下降趋势的流域,如黄河流域[32]与海河流域[33]等北方缺水地区,适应性调度的主要目标应是在水文变异导致水资源不足的情况下,如何通过适应性调度增加洪水资源的利用量,有待进一步研究.
| [1] |
Wang ZZ, Zhang LL, Cheng L et al. Optimizing operating rules for a reservoir system in northern China considering ecological flow requirements and water use priorities. Journal of Water Resources Planning and Management, 2020, 146(7): 04020051. DOI:10.1061/(asce)wr.1943-5452.0001236 |
| [2] |
Wang BD, Zhou HC. Research on dynamic control of reservoir normal elevation in flood season and applications. Beijing: National Hydraulic and Hydroelectric Publication House, 2006. [王本德, 周惠成. 水库汛限水位动态控制理论与方法及其运用. 北京: 中国水利水电出版社, 2006.]
|
| [3] |
Ministry of Water Resources of the People's Republic of China. China statistical yearbook of water resources 2018. Beijing: China Water & Power Press, 2018. [中华人民共和国水利部. 中国水利统计年鉴2018. 北京: 中国水利水电出版社, 2018.]
|
| [4] |
Zhang JY, Wang GQ, Jin JL et al. Evolution and variation characteristics of the recorded runoff for the major rivers in China during 1956-2018. Advances in Water Science, 2020, 31(2): 153-161. [张建云, 王国庆, 金君良等. 1956—2018年中国江河径流演变及其变化特征. 水科学进展, 2020, 31(2): 153-161.] |
| [5] |
Wang J, Xu YP, Wang YF et al. Impacts of anthropogenic activity on the response of water level to rainfall in the urbanized plain river network: A case study in the Hangzhou-Jiaxing-Huzhou region of Taihu Basin. J Lake Sci, 2019, 31(3): 779-787. [王杰, 许有鹏, 王跃峰等. 平原河网地区人类活动对降雨-水位关系的影响——以太湖流域杭嘉湖地区为例. 湖泊科学, 2019, 31(3): 779-787. DOI:10.18307/2019.0316] |
| [6] |
Song SB, Cheng L, Wang ZZ. Models of the return period calculation for seasonal flood. Journal of Hydraulic Engineering, 2018, 49(5): 523-534. [宋松柏, 程亮, 王宗志. 分期设计洪水重现期计算模型研究. 水利学报, 2018, 49(5): 523-534.] |
| [7] |
Liang ZM, Hu YM, Wang J. Advances in hydrological frequency analysis of non-stationary time series. Advances in Water Science, 2011, 22(6): 864-871. [梁忠民, 胡义明, 王军. 非一致性水文频率分析的研究进展. 水科学进展, 2011, 22(6): 864-871.] |
| [8] |
Milly PC, Betancourt J, Falkenmark M et al. Climate change. Stationarity is dead: Whither water management? Science, 2008, 319(5863): 573-574. DOI:10.1126/science.1151915 |
| [9] |
Wu ZY, Xie P, Sang YF et al. Moving correlation coefficient-based method for the detection of change-points in hydrological time series. Journal of Hydraulic Engineering, 2017, 48(12): 1473-1481, 1489. [吴子怡, 谢平, 桑燕芳等. 水文序列跳跃变异点的滑动相关系数识别方法. 水利学报, 2017, 48(12): 1473-1481, 1489.] |
| [10] |
Petrow T, Merz B. Trends in flood magnitude, frequency and seasonality in Germany in the period 1951-2002. Journal of Hydrology, 2009, 371(1/2/3/4): 129-141. DOI:10.1016/j.jhydrol.2009.03.024 |
| [11] |
Xie P, Chen GC, Lei HF et al. Hydrological alteration diagnosis system. Journal of Hydroelectric Engineering, 2010, 29(1): 85-91. [谢平, 陈广才, 雷红富等. 水文变异诊断系统. 水力发电学报, 2010, 29(1): 85-91.] |
| [12] |
Song SB, Li Y, Cai MK. Methods of frequency analysis for hydrologic data with jump up components. Journal of Hydraulic Engineering, 2012, 43(6): 734-739, 748. [宋松柏, 李扬, 蔡明科. 具有跳跃变异的非一致分布水文序列频率计算方法. 水利学报, 2012, 43(6): 734-739, 748.] |
| [13] |
Guo SL, Liu ZJ, Xiong LH. Advances and assessment on design flood estimation methods. Journal of Hydraulic Engineering, 2016, 47(3): 302-314. [郭生练, 刘章君, 熊立华. 设计洪水计算方法研究进展与评价. 水利学报, 2016, 47(3): 302-314.] |
| [14] |
Wang GQ, Zhang JY, He RM. Impacts of environmental change on runoff in Fenhe river basin of the middle Yellow River. Advances in Water Science, 2006, 17(6): 853-858. [王国庆, 张建云, 贺瑞敏. 环境变化对黄河中游汾河径流情势的影响研究. 水科学进展, 2006, 17(6): 853-858. DOI:10.3321/j.issn:1001-6791.2006.06.017] |
| [15] |
Wang ZJ, Yang F, Zhao JS et al. New approach for water resources assessment based on distributed hydrological model. Journal of Hydraulic Engineering, 2008, 39(12): 1279-1285. [王忠静, 杨芬, 赵建世等. 基于分布式水文模型的水资源评价新方法. 水利学报, 2008, 39(12): 1279-1285. DOI:10.3321/j.issn:0559-9350.2008.12.001] |
| [16] |
Han RG, Feng P. Effects of sublayer and land-cover change on flood in Daqinghe River Basin. Journal of Arid Land Resources and Environment, 2010, 24(8): 27-30. [韩瑞光, 冯平. 流域下垫面变化对洪水径流影响的研究. 干旱区资源与环境, 2010, 24(8): 27-30.] |
| [17] |
Xia J, Shi W. Perspective on water security issue of changing environment in China. Journal of Hydraulic Engineering, 2016, 47(3): 292-301. [夏军, 石卫. 变化环境下中国水安全问题研究与展望. 水利学报, 2016, 47(3): 292-301.] |
| [18] |
Wang Y, Peng SM, Zheng XK. Key scientific issues of water allocation plan optimization and comprehensive operation for Yellow River Basin. Advances in Water Science, 2018, 29(5): 614-624. [王煜, 彭少明, 郑小康. 黄河流域水量分配方案优化及综合调度的关键科学问题. 水科学进展, 2018, 29(5): 614-624.] |
| [19] |
Zhang W, Wang X, Lei XH et al. Adaptive reservoir operating rules based on the Dempster-Shafer evidence theory. Advances in Water Science, 2018, 29(5): 685-695. [张玮, 王旭, 雷晓辉等. 一种基于DS理论的水库适应性调度规则. 水科学进展, 2018, 29(5): 685-695.] |
| [20] |
Wu SY, Zhao JS, Lei XH et al. Impacts of climate change on operation of Xin'an River reservoir and adaption strategies. Journal of Hydroelectric Engineering, 2017, 36(1): 50-58. [吴书悦, 赵建世, 雷晓辉等. 气候变化对新安江水库调度影响与适应性对策. 水力发电学报, 2017, 36(1): 50-58.] |
| [21] |
Guo SL, Chen JH, Liu P et al. State-of-the-art review of joint operation for multi-reservoir systems. Advances in Water Science, 2010, 21(4): 496-503. [郭生练, 陈炯宏, 刘攀等. 水库群联合优化调度研究进展与展望. 水科学进展, 2010, 21(4): 496-503.] |
| [22] |
Mei YD, Xiong Y, Chen LH. A dynamic programming method for the multi-purpose operation of cascade reservoirs. Journal of Hydroelectric Engineering, 2007, 26(2): 1-4. [梅亚东, 熊莹, 陈立华. 梯级水库综合利用调度的动态规划方法研究. 水力发电学报, 2007, 26(2): 1-4. DOI:10.3969/j.issn.1003-1243.2007.02.001] |
| [23] |
Sun P, Wang LP, Jiang ZQ et al. Application of two multi-dimensional dynamic programming algorithms in optimization of cascade reservoirs operation. Journal of Hydraulic Engineering, 2014, 45(11): 1327-1335. [孙平, 王丽萍, 蒋志强等. 两种多维动态规划算法在梯级水库优化调度中的应用. 水利学报, 2014, 45(11): 1327-1335.] |
| [24] |
Chen GC, Xie P. Slide F test of change-point analysis. Journal of China Hydrology, 2006, 26(2): 57-60. [陈广才, 谢平. 水文变异的滑动F识别与检验方法. 水文, 2006, 26(2): 57-60.] |
| [25] |
Wan RR, Yang GS. Progress in the hydrological impact and flood response of watershed land use and land cover change. J Lake Sci, 2004, 16(3): 258-264. [万荣荣, 杨桂山. 流域土地利用/覆被变化的水文效应及洪水响应. 湖泊科学, 2004, 16(3): 258-264. DOI:10.18307/2004.0311] |
| [26] |
Xu B, Xie P, Tan YY et al. Analysis of flood returning to main channel influence on the flood control ability of Xi River. Journal of Hydroelectric Engineering, 2014, 33(2): 65-72. [许斌, 谢平, 谭莹莹等. 洪水归槽影响下西江中游防洪能力分析. 水力发电学报, 2014, 33(2): 65-72.] |
| [27] |
Zhong PA, Tang HW. Thinking and preliminary practice of comprehensive treatment of the middle and lower reaches of the Huaihe River basin. Advances in Water Science, 2020, 31(5): 746-753. [钟平安, 唐洪武. 淮河中下游洪涝综合治理的思考与初探. 水科学进展, 2020, 31(5): 746-753.] |
| [28] |
Wei YM, Fan Y, Jin JL. System theory for risk analysis of flood disaster. Journal of Management Sciences in China, 2001, 4(2): 7-11, 44. [魏一鸣, 范英, 金菊良. 洪水灾害风险分析的系统理论. 管理科学学报, 2001, 4(2): 7-11, 44.] |
| [29] |
Jin JL, Wang YT, Wei YM et al. Theoretical analysis frame based on general entropy and intelligence integration methodology for flood disaster risk management. Advances in Water Science, 2009, 20(6): 894-900. [金菊良, 王银堂, 魏一鸣等. 洪水灾害风险管理广义熵智能分析的理论框架. 水科学进展, 2009, 20(6): 894-900.] |
| [30] |
Cheng CT, Wang BD. Fuzzy optimal model of reservoir flood operation by means of heuristic approach and human-computer interaction technique. Journal of Hydraulic Engineering, 1995, 26(11): 71-76. [程春田, 王本德. 启发式与人机交互相结合的水库防洪模糊优化调度模型. 水利学报, 1995, 26(11): 71-76.] |
| [31] |
Wang WS, Jin JL, Li YQ. Advances in stochastic simulation of Hydrology. Advances in Water Science, 2007, 18(5): 768-775. [王文圣, 金菊良, 李跃清. 水文随机模拟进展. 水科学进展, 2007, 18(5): 768-775.] |
| [32] |
Wang YM, Tu ZQ, Chang JX et al. A study on the method of determining the staging characteristics of reservoir drought control. Journal of Natural Disasters, 2020, 29(1): 112-120. [王义民, 屠子倩, 畅建霞等. 水库抗旱调度分期特征确定方法研究. 自然灾害学报, 2020, 29(1): 112-120. DOI:10.13577/j.jnd.2020.0112] |
| [33] |
Zhao JS, Wang ZJ, Qin T et al. Analysis on evolution of water resources carrying capacity of Haihe River basin. Journal of Hydraulic Engineering, 2008, 39(6): 647-651, 658. [赵建世, 王忠静, 秦韬等. 海河流域水资源承载能力演变分析. 水利学报, 2008, 39(6): 647-651, 658.] |
 2021, Vol. 33
2021, Vol. 33 


