(2: 宁波弘泰水利信息科技有限公司, 宁波 315000)
(2: Ningbo Hong Tai Water Conservancy Information Technology Company, Ningbo 315000, P. R. China)
洪水预报误差来源多且影响复杂,洪水预报至今仍是水情预报的难点[1-2]. 实时修正技术是保证实时洪水预报精度的关键[3]. 现有误差修正方法大多没有考虑流域产汇流过程的物理基础,主要以控制断面误差为基础,将预报对象的误差与模型分离,本质上是“黑箱”分析方法,普遍存在外延性差、预见期损失等问题[4-5]. 洪水预报误差修正研究中,通常需要考虑模型自变量变化与模型计算结果误差之间的关系. 函数微分中自变量增量与因变量增量之间的微分响应关系,能够较好地描述复杂系统中各影响因素之间的变化关系[6-7]. 包为民等提出将微分响应关系用于洪水预报误差修正研究,具有物理基础强、不增加参数、不损失预见期等优点[8]. 现有研究主要利用微分响应方法对流域面平均降雨[9-10]、面平均产流[11-13]、面平均状态变量[14-16]等进行修正,没有考虑洪水预报误差的空间分布差异.
流域降水时空分布和下垫面分布复杂,流域产汇流过程呈高度非线性、时空变化大[17]. 目前洪水预报误差研究基本上是对各种误差源等权看待,对误差时空变化考虑不足会降低误差修正效果,影响洪水预报精度. 有研究利用雨量站网密度与洪水预报误差分配比例之间的定量关系将洪水预报总误差划分为面雨量输入误差和模型参数误差[18],利用各单元计算流量与各单元计算流量和的比例对流域面平均雨量估计值进行各单元分配以减小各单元面雨量误差[19]. 洪水预报误差修正大多基于流域系统输出信息,虽然该信息能够反映计算过程中各阶段误差的最终结果[20],但难以区分反映各阶段误差对洪水预报的影响[21]. 从流域系统输出的误差序列中辨析误差贡献,考虑误差时空变化进行实时修正有利于提高洪水预报精度.
本文针对洪水预报空间误差修正困难的问题,基于水文系统微分响应关系构建了流域产流分单元修正方法,并比较分析了在不同预见期时流域产流分单元修正、流域面平均产流修正和自回归修正的效果. 该研究对于流域水文要素时空误差修正、洪水预报精度提高具有重要意义和实用价值.
1 方法介绍 1.1 水文系统微分响应修正方法水文模型的输入、状态变量、参数等任一变量的改变,都会引起流域出口断面流量的变化. 把流域水文模型概化为一个复杂函数,利用微分建立自变量增量与因变量增量之间的响应关系:
| $ \text{d}Q=~\frac{\partial f}{\partial X}\text{d}X $ | (1) |
式中, Q为模型因变量(模型输出);X为模型自变量(输入变量、状态变量、参数等);∂f/∂X为变量X的微分响应.
式(1)中自变量增量即为模型影响因素的误差,因变量增量即为模型计算结果的误差. 式(1)的矩阵形式为:
| $ \Delta Q=U\Delta X+\xi $ | (2) |
式中, ΔQ为实测值与计算值的差值序列; Um×n为雅可比矩阵(微分响应矩阵),U=[u1, …, uj, …, un],列向量
采用正则化最小二乘法求解式(2),得变量X的误差估计量为[16]:
| $\Delta X={{({{U}^{T}}U+\beta I)}^{-1}}{{U}^{T}}\Delta Q $ | (3) |
式中, I为单位矩阵, β为正则化系数.
修正后的变量X′为:
| $ {X}'=X+\Delta X $ | (4) |
流域水文系统是一个非线性系统,考虑非线性问题线性化的影响,采用逐步迫近进行反演求解[22]:
| ${{X}^{(k+1)}}={{X}^{(k)}}+\Delta {{X}^{(k)}} $ | (5) |
式中, 上标k为迫近次数, X(k)为第k次迭代的变量估计值, ΔX(k)为第k次迭代的变量误差估计值.
将修正后的变量重新输入模型进行计算可得到修正后的模型结果. 基于水文系统微分响应关系建立误差修正方法,利用了产汇流模型结构的物理基础,概念清晰,计算简便.
1.2 流域产流分单元微分响应修正方法流域水文模型中每个子过程可以概化为一个系统,多个密切联系的子过程也可以概化为一个系统. 新安江模型包括蒸散发计算、产流计算、分水源计算和汇流计算[23],可以将蒸散发计算和产流计算作为一个系统(记为E_R系统),水源划分和汇流计算作为一个系统(记为R_Q系统). 产流计算是对降雨在数量上的再分配,产流量是影响水量平衡的重要因素,在洪水预报中起着重要作用. 对于产流微分响应修正,可通过R_Q系统利用流域出口流量反演修正产流(图 1).

|
图 1 新安江模型产流修正示意图(P为降雨、EM为水面蒸发、R为产流、Q为流域出口流量) Fig.1 Runoff correction strategy for the Xin'anjiang model |
采用新安江模型进行流域洪水预报,通常需进行流域划分. 假设流域划分为s个单元流域,流域出口流量对各单元流域产流的响应可以表达为:
| $ Q=f({{R}_{i}}, t)\ (i=1\sim s) $ | (6) |
式中, i为单元流域编码, s为单元流域数目, Ri=[ri, 1, …, ri, j, …, ri, n]T为第“i”单元流域产流.
考虑误差空间分布,构建流域产流分单元微分响应修正(又称流域产流分块修正或时空产流修正),记为SDR,如图 2a所示,计算步骤如下:
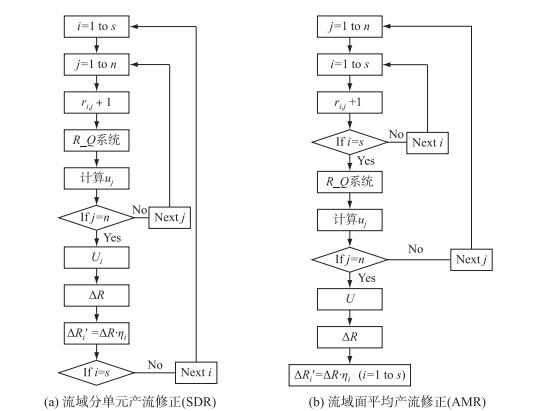
|
图 2 基于微分响应的流域产流修正流程图 Fig.2 Scheme of runoff correction based on differential response |
(1) 计算j时刻各单元流域产流量Ri (i=1~s),将i单元流域j时刻计算产流量ri, j加上1个单位(其他时刻其他单元流域产流量保持不变)代入R_Q系统计算得到新的流量系列,减去原来的流量系列,得到i单元流域U矩阵j列uj.
(2) 在不同时刻(j=1~n)重复步骤(1)即可得到i单元流域U矩阵所有列.
(3) 计算产流误差估计值ΔR,根据i单元流域面积占全流域面积的比例将估计的产流误差分配给i单元流域,得到i单元产流误差修正量为ΔR′ i =ΔR·ηi,其中ηi为i单元流域面积占全流域面积的比例.
(4) 重复步骤(1)~(3),可得到各单元流域U矩阵及相应的产流修正量.
已有研究采用流域面平均产流修正[11-13],记为AMR,如图 2b所示,计算流程如下:
(1) 计算j时刻各单元流域产流量Ri(i=1~s),将各单元流域j时刻计算产流量加上1个单位(其他时刻产流量保持不变)代入R_Q系统计算得到新的流量系列,减去原来的流量系列,得到全流域U矩阵j列uj.
(2) 在不同时刻(j=1~n)重复步骤(1)就得到U所有列.
(3) 计算产流量误差估计值ΔR.
(4) 根据单元流域面积占全流域面积的比例将产流误差估计值分配给各单元流域,得到各单元产流误差修正量ΔR′ i.
流域产流分单元微分响应修正(SDR)和流域面平均产流微分响应修正(AMR)的不同点在于微分响应矩阵的构建和产流估计误差的分配. AMR在求解微分响应矩阵时所有单元流域产流量均增加1个单位,所求得的微分响应反映了流域出口流量对流域平均产流变化的响应. SDR分别计算不同单元流域对应的微分响应,通过各单元流域微分响应提取流域出口断面流量中包含的空间(单元流域)信息,增加了信息利用. AMR微分响应矩阵为2维数组Um×n,SDR微分响应矩阵为3维数组Um×n×s. AMR是将产流估计误差按面积比例分配给各个单元流域,而SDR是将利用单元流域微分响应求得的误差估计值分配给相应的单元流域.
2 应用检验 2.1 实例概况将构建的微分响应误差修正方法用于修正三水源新安江模型计算产流. (1)比较SDR和AMR的修正效果. (2)比较SDR、AMR与二阶自回归(AR)在采用不同预见期时的修正效果.
选择具有不同雨量站点密度和不同洪水特点的淮河大坡岭流域和闽江七里街流域为研究区域. 流域图如图 3,流域信息如表 1. 采用泰森多边形法,将大坡岭流域划分为13个单元流域,将七里街流域划分为41个单元流域,每个单元流域有一个雨量站.
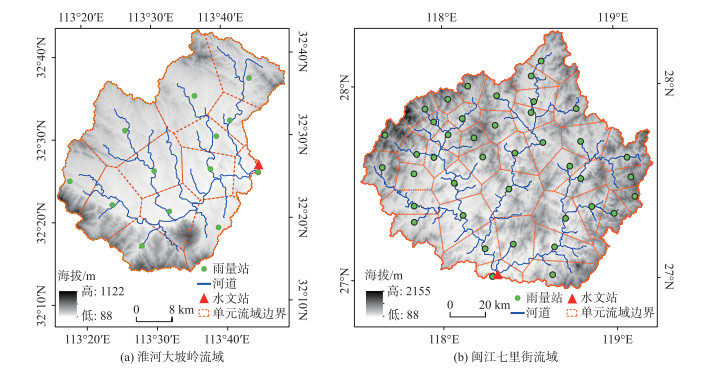
|
图 3 研究区域流域图 Fig.3 Location of the study basins |
| 表 1 流域信息 Tab. 1 Informations of two basins |
采用三水源新安江模型进行流域洪水模拟. 大坡岭流域采用1987—2009年14场洪水资料,从起涨到洪峰出现的平均历时为36.3 h,其中10场用于新安江模型参数率定,4场用于检验. 七里街流域采用1988—1999年20场洪水资料,从起涨到洪峰出现的平均历时为77.9 h,其中15场用于新安江模型参数率定,5场用于检验.
微分响应修正采用逐步迫近求解,以误差均方差为目标函数判断是否进行下一次迭代. 通过微分响应修正时所使用实测流量资料长度设置了一系列不同预见期,预见期越长所用实测流量时段数越少. 采用径流深相对误差(RRE)、洪峰相对误差(RPE)、误差均方差(RMSE)和Nash-Sutcliffe系数(NSE)[24]评估计算结果.
2.2 结果分析淮河大坡岭流域和闽江七里街流域的洪水模拟结果分别见表 2和表 3. 表中
| 表 2 大坡岭流域洪水模拟结果 Tab. 2 Flood simulation results in the Dapoling Basin |
| 表 3 七里街流域洪水模拟结果 Tab. 3 Flood simulation results in the Qilijie Basin |
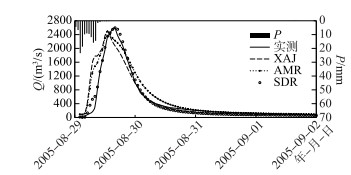
|
图 4 大坡岭流域20050829洪水过程线 Fig.4 Hydrographs for the flood event 20050829 in the Dapoling Basin |

|
图 5 大坡岭流域不同预见期时洪水修正结果比较 Fig.5 Mean evaluation measures with different lead times in the Dapoling Basin |
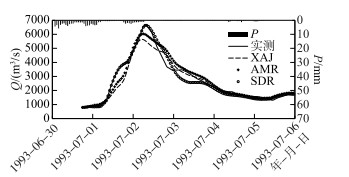
|
图 6 七里街流域19930630洪水过程线 Fig.6 Hydrographs for the flood event 19930630 in the Qilijie Basin |
|
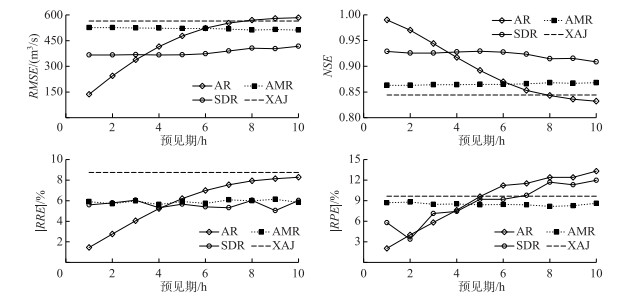
图 7 七里街流域不同预见期时洪水修正结果比较 Fig.7 Mean evaluation measures with different lead times in the Qilijie Basin |
由表 2可知,在淮河大坡岭流域,新安江模型经过SDR和AMR修正后计算精度提高了. SDR修正效果优于AMR,经SDR修正后
由表 3可知,在闽江七里街流域,采用SDR和AMR修正后新安江模型计算效果提高了,SDR修正效果总体上优于AMR. 与AMR结果相比,SDR修正后
大坡岭流域和七里街流域所采用的历史洪水从起涨到洪峰出现的平均历时差别较大,能用于误差修正的实测流量个数不同,微分响应修正均获得了较好的修正效果. 在七里街流域部分雨量站雨量资料缺乏,采用邻近站资料替代,雨量资料时空误差较大,通过模型计算引起的产流时空误差也较大. 对于时空误差较大的洪水,AMR修正效果有限,SDR修正效果较好. 实例中微分响应修正以误差均方差作为判断条件进行逐步迫近反演求解,SDR修正和AMR修正的平均迭代次数均小于10次. 经误差修正后,误差均方差减小了,NSE系数提高了,但并不能保证所有洪水的洪峰和径流深模拟精度都提高,可以考虑采用兼顾洪峰和洪水过程的多目标函数作为判断条件.
微分响应修正是基于流域出口流量与被修正量之间的微分响应关系建立的反馈修正方法,理论上可用于修正模型任一自变量,实际应用中通常用于修正主要误差. 在洪水预报中可用于修正降雨、产流、参数、状态变量等,修正效果取决于被修正变量是否是主要误差来源. 产流计算受诸多误差影响,模型输入、状态变量等误差经蒸散发计算和产流计算会传播累积影响计算产流量,产流修正很有必要. 在大坡岭流域预见期小于2 h,在七里街流域预见期小于4 h时,AR修正效果优于SDR,主要是因为AR修正是直接对所有误差影响下的流域出口流量进行修正. 但AR修正效果取决于输出结果误差之间的相关性,随着预见期增大修正效果明显变差.
结合新安江模型的产流微分响应修正是将分水源和汇流部分作为响应系统,利用流域出口流量误差信息反馈修正产流量,将修正后的产流重新输入模型进行后续的分水源、坡地汇流和河道汇流计算,进而修正流域出口断面流量. 流域出口断面流量是所有误差影响的最终结果,对其进行时空误差辨识很难. SDR修正建立了各单元流域产流与流域出口断面流量之间的微分响应关系,利用各单元流域微分响应关系可以从流域出口断面流量中提取有效的空间信息用于产流量修正. 基于微分响应的流域分单元误差修正思路可为分布式流域水文模型误差修正研究提供一种有效途径,进一步可通过水文系统各要素引起的微分响应关系研究水文要素时空变化,成果应用可以有效提高实时洪水预报精度.
3 结论1) 基于微分响应构建了流域产流分单元修正方法(SDR),利用汇流系统物理基础建立了各单元流域产流误差与流域出口流量误差之间的响应关系,采用正则化最小二乘法结合逐步迫近求解产流修正估计量,对产流误差修正量进行时空分配实现流域产流分单元修正.
2) 在淮河大坡岭流域和闽江七里街流域结合新安江模型进行方法检验,结果表明:采用产流微分响应修正后的模型效果优于原水文模型效果;SDR效果总体优于AMR;随着预见期增大,SDR和AMR的修正效果优于AR.
3) 微分响应分单元修正能通过水文系统从流域出口信息中提取有效的空间信息用于误差修正,考虑了误差的空间分布,使用简单,不改变原模型结构,可与不同水文模型结合用于修正不同时空误差,对于时空误差研究具有重要意义.
| [1] |
Pianosi F, Wagener T. Understanding the time-varying importance of different uncertainty sources in hydrological modelling using global sensitivity analysis. Hydrological Processes, 2016, 30(22): 3991-4003. DOI:10.1002/hyp.10968 |
| [2] |
Kerr RA. HYDROLOGY: river-level forecasting shows No detectable progress in 2 decades. Science, 2007, 316(5831): 1555a. DOI:10.1126/science.316.5831.1555a |
| [3] |
Bao WM. A discussion on information utilization for flood forecasting. Journal of China Hydrology, 2006, 26(2): 18-21. [包为民. 洪水预报信息利用问题研究与讨论. 水文, 2006, 26(2): 18-21. DOI:10.3969/j.issn.1000-0852.2006.02.005] |
| [4] |
Madsen H, Skotner C. Adaptive state updating in real-time river flow forecasting-a combined filtering and error forecasting procedure. Journal of Hydrology, 2005, 308(1/2/3/4): 302-312. DOI:10.1016/j.jhydrol.2004.10.030 |
| [5] |
Li M, Wang QJ, Bennett JC et al. A strategy to overcome adverse effects of autoregressive updating of streamflow forecasts. Hydrology and Earth System Sciences, 2015, 19(1): 1-15. DOI:10.5194/hess-19-1-2015 |
| [6] |
Fang SG, Zhang QH, Lin YQ. An interval inverse solution method based on Taylor series expansion. Chinese Journal of Computational Mechanics, 2015, 32(6): 796-802. [方圣恩, 张秋虎, 林友勤. 基于泰勒级数展开的区间反演方法. 计算力学学报, 2015, 32(6): 796-802. DOI:10.7511/jslx201506013] |
| [7] |
Kirchner JW. Catchments as simple dynamical systems: Catchment characterization, rainfall-runoff modeling, and doing hydrology backward. Water Resources Research, 2009, 45(2): W02429. DOI:10.1029/2008WR006912 |
| [8] |
Bao WM, Si W, Shen GH et al. Runoff error updating based on unit hydrograph inversion. Advances in Water Science, 2012, 23(3): 317-322. [包为民, 司伟, 沈国华等. 基于单位线反演的产流误差修正. 水科学进展, 2012, 23(3): 317-322.] |
| [9] |
Si W, Bao WM, Gupta HV. Updating real-time flood forecasts via the dynamic system response curve method. Water Resources Research, 2015, 51(7): 5128-5144. DOI:10.1002/2015WR017234 |
| [10] |
Si W, Bao WM, Qu SM et al. Real-time flood forecast updating method based on mean areal rainfall error correction. J Lake Sci, 2018, 30(2): 533-541. [司伟, 包为民, 瞿思敏等. 基于面平均雨量误差修正的实时洪水预报修正方法. 湖泊科学, 2018, 30(2): 533-541. DOI:10.18307/2018.0224] |
| [11] |
Zhang XQ, Liu KX, Bao WM et al. Runoff error proportionality coefficient correction method based on system response. Advances in Water Science, 2014, 25(6): 789-796. [张小琴, 刘可新, 包为民等. 产流误差比例系数的系统响应修正方法. 水科学进展, 2014, 25(6): 789-796.] |
| [12] |
Liu KX, Zhang XQ, Bao WM et al. A system response correction method with runoff error smooth matrix. Journal of Hydraulic Engineering, 2015, 46(8): 960-966. [刘可新, 张小琴, 包为民等. 产流误差平稳矩阵的系统响应修正方法. 水利学报, 2015, 46(8): 960-966.] |
| [13] |
Si W, Bao WM, Qu SM. Runoff error correction in real-time flood forecasting based on dynamic system response curve. Advances in Water Science, 2013, 24(4): 497-503. [司伟, 包为民, 瞿思敏. 洪水预报产流误差的动态系统响应曲线修正方法. 水科学进展, 2013, 24(4): 497-503.] |
| [14] |
Bao WM, Que JJ, Lai SZ et al. Free-water storage error correction based on dynamic system response in flood forecasting. Advances in Water Science, 2015, 26(3): 365-371. [包为民, 阙家骏, 赖善证等. 洪水预报自由水蓄量动态系统响应修正方法. 水科学进展, 2015, 26(3): 365-371.] |
| [15] |
Sun Y, Bao W, Jiang P et al. Development of multivariable dynamic system response curve method for real-time flood forecasting correction. Water Resources Research, 2018, 54(7): 4730-4749. DOI:10.1029/2018WR022555 |
| [16] |
Bao WM, Sun YQ, Zhou JW et al. A new version of system response method for error correction based on total least squares. Journal of Hydraulic Engineering, 2017, 48(5): 560-567. [包为民, 孙逸群, 周俊伟等. 基于总体最小二乘法的系统响应修正方法. 水利学报, 2017, 48(5): 560-567.] |
| [17] |
Beven K. Towards an alternative blueprint for a physically based digitally simulated hydrologic response modelling system. Hydrological Processes, 2002, 16(2): 189-206. DOI:10.1002/hyp.343 |
| [18] |
Liang ZM, Huang YX, Hu YM et al. The entire-process correction approach for flood forecasting. South-to-North Water Transfers and Water Science & Technology, 2020, 18(1): 1-10, 17. [梁忠民, 黄一昕, 胡义明等. 全过程联合校正的洪水预报修正方法. 南水北调与水利科技, 2020, 18(1): 1-10, 17.] |
| [19] |
Si W, Gupta HV, Bao WM et al. Improved dynamic system response curve method for real-time flood forecast updating. Water Resources Research, 2019, 55(9): 7493-7519. DOI:10.1029/2019WR025520 |
| [20] |
Tiedeman CR, Green CT. Effect of correlated observation error on parameters, predictions, and uncertainty. Water Resources Research, 2013, 49(10): 6339-6355. DOI:10.1002/wrcr.20499 |
| [21] |
Liu YQ, Gupta HV. Uncertainty in hydrologic modeling: Toward an integrated data assimilation framework. Water Resources Research, 2007, 43(7): W07401. DOI:10.1029/2006WR005756 |
| [22] |
Zhang XQ, Bao WM, Sun YQ. Enhancing the hydrologic system differential response method for flood forecasting correction. Journal of Hydrology, 2021, 592: 125793. DOI:10.1016/j.jhydrol.2020.125793 |
| [23] |
Zhao RJ. The Xinanjiang model applied in China. Journal of Hydrology, 1992, 135(1/2/3/4): 371-381. DOI:10.1016/0022-1694(92)90096-E |
| [24] |
Nash JE, Sutcliffe JV. River flow forecasting through conceptual models part Ⅰ-A discussion of principles. Journal of Hydrology, 1970, 10(3): 282-290. DOI:10.1016/0022-1694(70)90255-6 |
 2021, Vol. 33
2021, Vol. 33 

