洪水预报是一项重要的防洪减灾非工程措施[1]. 虽然洪水预报理论和技术得到了长足发展[2-3],但仍面临挑战:一方面,现行的水文模型理论与方法尚难以对流域水文物理过程进行精准地模拟和预报,另一方面,气候变化与高强度人类活动的影响导致水文事件发生的时空格局复杂多变,给洪水预报无形中增加了难度[4-5]. 因此,在实时洪水预报中,实时校正技术作为保障和提升洪水预报精度的最后一道关口,必不可少.
实时校正方法的研究较多[6-9],从实用角度,一般以对单河段的校正居多,即只利用河段上下游断面的实时信息进行下断面预报误差的修正和更新. 例如:王船海等[10]提出了基于卡尔曼滤波校正技术的单一河道水动力学模型,通过局部校正对全河道预报起带动作用;常露等[11]建立了基于K-最近邻非参数实时校正模型的河道洪水预报系统,可对具有行蓄洪区的河道流域进行模拟与校正;徐兴亚等[12]建立了基于粒子滤波数据同化算法的河道洪水实时概率预报模型,不仅可以直接校正水位,同时也可以有效地校正流量和糙率;高益辉等[13]提出了将自适应自回归模型与河道水流演进基本方程相结合的多点联合校正方法,可对并联的单河段汇流系统进行实时校正;梁忠民等[14]提出了基于动力系统反演理论的马斯京根流量演算误差校正方法,对单河段洪水演算过程中马斯京根法的3类误差源,分别构建3种误差演算方程并进行误差校正. 上述这些方法的特点是只利用本河段上下游断面的实测信息,所以计算简单、应用方便,但也因其忽略了整个河道干支流其它断面的实测和校正信息,有时并不能取得理想效果,且校正的有效预见期受限. 实际的河流水系结构一般都比较复杂,断面或河段间存在水力联系,下游某一断面的预报误差受上游多断面的共同影响,因此,在实时校正中,可以充分利用河系中河段之间的信息联系,考虑上游关联断面对下游校正断面的影响,降低误差在汇流过程中的累积传播效应,以提高校正精度.
为此,本文引入马斯京根法汇流演算矩阵方程[15]描述河系上下游之间的水力联系,并与动力系统误差反演方程[14]结合,提出一种适合复杂河流系统的多河段联合校正方法,并在大渡河上游流域进行了示例应用.
1 方法原理介绍 1.1 复杂河流系统图 1a所示是一个自然的河流系统,系统内的长河段可划分为n个子河段(从1级河流至n级河流)和n+1个河段断面(从第0个断面至第n个断面,其中:第0个断面为河源断面,第n个断面为流域出口断面). 由于该系统各级河流的上下游断面之间存在水力联系,各断面流量Qi(i=1, …, n)的来源包含两部分:①第i个河段的上断面入流,即第i-1个断面的控制面积以上降水径流Qi-1;②第i个河段的区间入流qi. 相应地,各断面流量的预报误差也由两部分组成:①上断面入流的预报误差;②区间入流的预报误差. 因此,对于一个如图 1a的复杂河流系统,其出口断面流量预报误差的大小,是由上游多个区间和断面的预报误差共同作用与影响决定的. 而对于图 1b和1c所示的概化的单断面/单河段系统,认为流域下游出口断面仅受该断面或上游断面的影响. 其中,图 1b是将图 1a中的复杂多河段河流系统简化成一个单断面系统,出口断面流量为Q;图 1c是将图 1a中的复杂多河段河流系统简化成一个单河段系统,下断面出口断面流量为QOut,上断面河源断面流量为QIn,河段区间入流为q.

|
图 1 自然的河流系统示意 Fig.1 Natural river system schematic |
基于动力系统误差反演的单断面校正模型,是直接对流域出口断面的预报误差进行校正,以提高洪水预报精度. 动力系统是指状态随时间变化的系统,可由特定的方程(如微分方程)描述. 动力系统反演则是指通过观测资料反求动力系统方程的过程[16-17]. 若以出口断面流量系列为研究对象(如图 1b所示),以一个受3个变量影响的系统为例.
依据出口断面流量的历史预报值和实测值,计算洪水预报误差:
| $ \left\{\begin{array}{l} \varepsilon(t)=Q_{\mathrm{m}}(t)-Q_{c}(t) \\ \varepsilon(t-\Delta t)=Q_{\mathrm{m}}(t-\Delta t)-Q_{\mathrm{c}}(t-\Delta t) \\ \varepsilon(t-2 \Delta t)=Q_{\mathrm{m}}(t-2 \Delta t)-Q_{\mathrm{c}}(t-2 \Delta t) \end{array}\right. $ | (1) |
式中,Qm(t)、Qm(t-Δt)、Qm(t-2Δt)分别为t、t-Δt、t-2Δt时刻的出口断面实测流量;Qc(t)、Qc(t-Δt)、Qc(t-2Δt)分别为t、t-Δt、t-2Δt时刻的出口断面预报流量;ε(t)、ε(t-Δt)、ε(t-2Δt)分别为t、t-Δt、t-2Δt时刻的出口断面洪水预报误差.
根据预报误差时间系列的相依特性,建立误差反演方程:
| $ \left\{\begin{array}{l} \mathrm{d} \varepsilon(t) / \mathrm{d} t=a_{1} \varepsilon(t)+a_{2} \varepsilon(t-\Delta t)+a_{3} \varepsilon(t-2 \Delta t)+a_{4} \varepsilon(t) \varepsilon(t-\Delta t)+a_{5} \varepsilon(t) \varepsilon(t-2 \Delta t)+a_{6} \varepsilon(t-\Delta t) \\ \ \ \ \ \ \ \ \ \varepsilon(t-2 \Delta t)+a_{7} \varepsilon(t)^{2}+a_{8} \varepsilon(t-\Delta t)^{2}+a_{9} \varepsilon(t-2 \Delta t)^{2}+a_{10} \varepsilon(t) \varepsilon(t-\Delta t) \varepsilon(t-2 \Delta t) \\ \mathrm{d} \varepsilon(t-\Delta t) / \mathrm{d} t=b_{1} \varepsilon(t)+b_{2} \varepsilon(t-\Delta t)+b_{3} \varepsilon(t-2 \Delta t)+b_{4} \varepsilon(t) \varepsilon(t-\Delta t)+b_{5} \varepsilon(t) \varepsilon(t-2 \Delta t)+ \\ \ \ \ \ \ \ \ \ b_{6} \varepsilon(t-\Delta t) \varepsilon(t-2 \Delta t)+b_{7} \varepsilon(t)^{2}+b_{8} \varepsilon(t-\Delta t)^{2}+b_{9} \varepsilon(t-2 \Delta t)^{2}+b_{10} \varepsilon(t) \varepsilon(t-\Delta t) \varepsilon(t-2 \Delta t) \\ \mathrm{d} \varepsilon(t-2 \Delta t) / \mathrm{d} t=c_{1} \varepsilon(t)+c_{2} \varepsilon(t-\Delta t)+c_{3} \varepsilon(t-2 \Delta t)+c_{4} \varepsilon(t) \varepsilon(t-\Delta t)+c_{5} \varepsilon(t) \varepsilon(t-2 \Delta t)+ \\ \ \ \ \ \ \ \ \ c_{6} \varepsilon(t-\Delta t) \varepsilon(t-2 \Delta t)+c_{7} \varepsilon(t)^{2}+c_{8} \varepsilon(t-\Delta t)^{2}+c_{9} \varepsilon(t-2 \Delta t)^{2}+c_{10} \varepsilon(t) \varepsilon(t-\Delta t) \varepsilon(t-2 \Delta t) \end{array}\right. $ | (2) |
式中,参数a1、a2、a3、a4、a5、a6、a7、a8、a9、a10,b1、b2、b3、b4、b5、b6、b7、b8、b9、b10,c1、c2、c3、c4、c5、c6、c7、c8、c9、c10是根据观测资料得到的方程特解.
将微分dε(t)/dt、dε(t-Δt)/dt、dε(t-2Δt)/dt转换成差分,得到t+Δt时刻预报误差ε(t+Δt) 的反演方程:
| $ \varepsilon(t+\Delta t)=\left[\begin{array}{l} a_{1} \varepsilon(t)+a_{2} \varepsilon(t-\Delta t)+a_{3} \varepsilon(t-2 \Delta t)+a_{4} \varepsilon(t) \varepsilon(t-\Delta t)+ \\ a_{5} \varepsilon(t) \varepsilon(t-2 \Delta t)+a_{6} \varepsilon(t-\Delta t) \varepsilon(t-2 \Delta t)+a_{7} \varepsilon(t)^{2}+ \\ a_{8} \varepsilon(t-\Delta t)^{2}+a_{9} \varepsilon(t-2 \Delta t)^{2}+a_{10} \varepsilon(t) \varepsilon(t-\Delta t) \varepsilon(t-2 \Delta t) \end{array}\right] \Delta t+\varepsilon(t) $ | (3) |
将估计的误差加到原出口断面预报流量Qc(t+Δt)上,则可得到校正后的出口断面预报流量Q′c(t+Δt):
| $ Q_{\mathrm{c}}^{\prime}(t+\Delta t)=Q_{\mathrm{c}}(t+\Delta t)+\varepsilon(t+\Delta t) $ | (4) |
基于动力系统反演理论的马斯京根流量演算的单河段校正模型[14](如图 1c所示),是考虑河段汇流演算过程中的上断面入流项、区间输入项以及马斯京根法模型本身误差,通过建立各项误差的非线性动力系统反演方程(建立原理同单断面校正模型),对各项误差进行校正,以提高河道下断面洪水预报精度.
考虑区间入流的单河段马斯京根法演算方程[18-19]可表示为:
| $ Q_{ \mathrm{Out}}^{t+\Delta t}=C_{0} Q_{\mathrm{In}}^{t+\Delta t}+C_{1} Q_{\mathrm{In}}^{t}+C_{2} Q_{\mathrm{Out}}^{t}+q^{t+\Delta t} $ | (5) |
其中:
| $ \left\{\begin{array}{l} C_{0}=\frac{0.5 \Delta t-K x}{0.5 \Delta t+K-K x} \\ C_{1}=\frac{0.5 \Delta t+K x}{0.5 \Delta t+K-K x} \\ C_{2}=\frac{-0.5 \Delta t+K-K x}{0.5 \Delta t+K-K x} \end{array}\right. $ | (6) |
式中,t+Δt为预报时刻;QInt+Δt、QOutt+Δt和qt+Δt分别为预报时刻的河道上断面预报流量、下断面预报流量和区间预报流量;QInt和QOutt分别为t时刻的河道上断面实测流量和下断面实测流量;C0、C1和C2均为演算系数,K为蓄量关系曲线的坡度,x为流量比重系数.
因此,马斯京根法预报结果的误差来源可分为3部分:上断面入流项QInt+Δt的误差εInt+Δt,区间输入项qt+Δt的误差εqt+Δt,以及马斯京根法方程本身的误差ε0t+Δt. 参照式(3)建立各部分误差的反演方程(由于区间流域往往缺乏实测洪水数据,一般将εqt+Δt和ε0t+Δt合成,统一进行系统反演),根据历史资料系列求得方程中的系数,则可计算出各项误差在未来t+Δt时刻的估计值:
| $ \left\{\begin{array}{l} \varepsilon_{\ln }^{t+\Delta t}=\left[a_{\mathrm{In}, 1} \varepsilon_{\mathrm{In}}^{t}+\cdots+a_{\ln , 10} \varepsilon_{\ln }^{t} \varepsilon_{\ln }^{t-\Delta t} \varepsilon_{\mathrm{In}}^{t-2 \Delta t}\right] \times \Delta t+\varepsilon_{\mathrm{In}}^{t} \\ \varepsilon_{q}^{t+\Delta t}=\left[a_{q, 1} \varepsilon_{q}^{t}+\cdots+a_{q, 10} \varepsilon_{q}^{t} \varepsilon_{q}^{t-\Delta t} \varepsilon_{q}^{t-2 \Delta t}\right] \times \Delta t+\varepsilon_{q}^{t} \\ \varepsilon_{0}^{t+\Delta t}=\left[a_{0,1} \varepsilon_{0}^{t}+\cdots+a_{0,10} \varepsilon_{0}^{t} \varepsilon_{0}^{t-\Delta t} \varepsilon_{0}^{t-2 \Delta t}\right] \times \Delta t+\varepsilon_{0}^{t} \end{array}\right. $ | (7) |
将估计的各项误差代入式(5)中,则可得到校正后的下断面预报值:
| $ Q_{\mathrm{Out}}^{t+\Delta t}=C_{0}\left(Q_{\mathrm{In}}^{t+\Delta t}+\varepsilon_{\mathrm{In}}^{t+\Delta t}\right)+C_{1} Q_{\mathrm{In}}^{t}+C_{2} Q_{\mathrm{Out}}^{t}+\left(q^{t+\Delta t}+\varepsilon_{q}^{t+\Delta t}\right)+\varepsilon_{0}^{t+\Delta t} $ | (8) |
本文提出的多河段联合校正模型,是采用马斯京根法矩阵方程描述多河段汇流过程,基于动力系统反演理论对各河段的区间入流误差进行演算,通过对各河段预报误差联合校正,最终降低河道出口断面洪水预报总误差.
1.3.1 马斯京根法矩阵方程对于多站点、多断面的河流系统,应考虑河道汇流时的流量演进和误差传递. 如图 1a所示的具有n个子河段的河流系统,表示成马斯京根法的矩阵形式(考虑区间入流)[15]:
| $ \left[\begin{array}{ccccc} 1 & 0 & \cdots & 0 & 0 \\ -C_{1,0} & 1 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & 0 \\ 0 & 0 & \cdots & -C_{n, 0} & 1 \end{array}\right]\left[\begin{array}{c} Q_{0}^{t+\Delta t} \\ Q_{1}^{t+\Delta t} \\ \vdots \\ Q_{n-1}^{t+\Delta t} \\ Q_{n}^{t+\Delta t} \end{array}\right]=\left[\begin{array}{ccccc} 0 & 0 & \cdots & 0 & 0 \\ C_{1,1} & C_{1,2} & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & C_{n-1,2} & 0 \\ 0 & 0 & \cdots & C_{n, 1} & C_{n, 2} \end{array}\right]\left[\begin{array}{c} Q_{0}^{t} \\ Q_{1}^{t} \\ \vdots \\ Q_{n-1}^{t} \\ Q_{n}^{t} \end{array}\right]+\left[\begin{array}{c} Q_{0}^{t+\Delta t} \\ q_{1}^{t+\Delta t} \\ \vdots \\ q_{n-1}^{t+\Delta t} \\ q_{n}^{t+\Delta t} \end{array}\right] $ | (9) |
式中,Q0t和Q0t+Δt分别为t时刻和t+Δt时刻的第1个子河段的上断面入流,Q1t、…、Qn-1t、Qnt和Q1t+Δt、…、Qn-1t+Δt、Qnt+Δt分别为t时刻和t+Δt时刻的第1个至第n个子河段的下断面出流,q1t+Δt、…、qn-1t+Δt、qnt+Δt分别为t+Δt时刻的第1个至第n个子河段的区间入流,C1, 0、C1, 1、C1, 2、…、Cn-1, 2、Cn, 0、Cn, 1、Cn, 2分别为各河段的马斯京根法演算系数.
以3段为例,如果各子河段的演算参数相等,则有:
| $ \left[\begin{array}{cccc} 1 & & & \\ -C_{0} & 1 & & \\ & -C_{0} & 1 & \\ & & -C_{0} & 1 \end{array}\right]\left[\begin{array}{c} Q_{0}^{t+\Delta t} \\ Q_{1}^{t+\Delta t} \\ Q_{2}^{t+\Delta t} \\ Q_{3}^{t+\Delta t} \end{array}\right]=\left[\begin{array}{cccc} 0 & & & \\ C_{1} & C_{2} & & \\ & C_{1} & C_{2} & \\ & & C_{1} & C_{2} \end{array}\right]\left[\begin{array}{c} Q_{0}^{t} \\ Q_{1}^{t} \\ Q_{2}^{t} \\ Q_{3}^{t} \end{array}\right]+\left[\begin{array}{c} Q_{0}^{t+\Delta t} \\ q_{1}^{t+\Delta t} \\ q_{2}^{t+\Delta t} \\ q_{3}^{t+\Delta t} \end{array}\right] $ | (10) |
考虑河道汇流演进过程中的区间入流误差以及第1个河段的上断面入流误差,基于动力系统反演理论的对预报误差演算. 第1个河段的上断面入流误差可根据历史预报值和实测值计算,而由于区间来水不好测量,区间入流误差系列根据该河段下断面实测流量扣除区间预报流量在下断面的响应来推算. 即:
| $ \left\{\begin{array}{l} \varepsilon_{0}^{t}=Q_{0, \mathrm{m}}^{t}-Q_{0, \mathrm{c}}^{t} \\ \delta_{1}^{t}=q_{1}^{t}-q_{1, \mathrm{c}}^{t}=Q_{1, \mathrm{m}}^{t}-\left[C_{0} Q_{0, \mathrm{c}}^{t}+C_{1} Q_{0, \mathrm{m}}^{t-\Delta t}+C_{2} Q_{1, \mathrm{m}}^{t-\Delta t}+q_{1, \mathrm{c}}^{t}\right] \\ \delta_{2}^{t}=q_{2}^{t}-q_{2, \mathrm{c}}^{t}=Q_{2, \mathrm{m}}^{t}-\left[C_{0} Q_{1, \mathrm{c}}^{t}+C_{1} Q_{1, \mathrm{m}}^{t-\Delta t}+C_{2} Q_{2, \mathrm{m}}^{t-\Delta t}+q_{2, \mathrm{c}}^{t}\right] \\ \delta_{3}^{t}=q_{3}^{t}-q_{3, \mathrm{c}}^{t}=Q_{3, \mathrm{m}}^{t}-\left[C_{0} Q_{2, \mathrm{c}}^{t}+C_{1} Q_{2, \mathrm{m}}^{t-\Delta t}+C_{2} Q_{3, \mathrm{m}}^{t-\Delta t}+q_{3, \mathrm{c}}^{t}\right] \end{array}\right. $ | (11) |
式中,ε0t为t时刻的第1个河段的上断面入流误差,Q0, mt为t时刻的第1个河段的上断面入流的实测值,Q0, ct为t时刻的第1个河段的上断面入流的预报值;δ1t、δ2t、δ3t分别为t时刻的第1、2、3个河段的区间入流误差系列,q1t、q2t、q3t分别为t时刻的3个河段的区间入流真值系列,q1,ct、q2, ct、q3, ct分别为t时刻的3个河段的区间入流预报值系列;Q0, ct、Q1, ct、Q2, ct为t时刻3个河段的上断面入流预报值系列,Q1, mt-Δt、Q2, mt-Δt、Q3, mt-Δt为t-Δt时刻的3个河段的下断面出流实测值系列.
参照式(3)建立各区间入流误差(第1个河段的上断面入流误差也可认为是该河段的旁侧入流误差)的动力系统反演方程:
| $ \left\{\begin{aligned} \varepsilon_{0}^{t+\Delta t} &=\left[a_{0,1} \varepsilon_{0}^{t}+a_{0,2} \varepsilon_{0}^{t-\Delta t}+a_{0,3} \varepsilon_{0}^{t-2 \Delta t}+\cdots+a_{0,10} \varepsilon_{0}^{t} \varepsilon_{0}^{t-\Delta t} \varepsilon_{0}^{t-2 \Delta t}\right] \times \Delta t+\varepsilon_{0}^{t} \\ \delta_{1}^{t+\Delta t} &=\left[a_{1,1} \delta_{1}^{t}+a_{1,2} \delta_{1}^{t-\Delta t}+a_{1,3} \delta_{1}^{t-2 \Delta t}+\cdots+a_{1,10} \delta_{1}^{t} \delta_{1}^{t-\Delta t} \delta_{1}^{t-2 \Delta t}\right] \times \Delta t+\delta_{1}^{t} \\ \delta_{2}^{t+\Delta t} &=\left[a_{2,1} \delta_{2}^{t}+a_{2,2} \delta_{2}^{t-\Delta t}+a_{2,3} \delta_{2}^{t-2 \Delta t}+\cdots+a_{2,10} \delta_{2}^{t} \delta_{2}^{t-\Delta t} \delta_{2}^{t-2 \Delta t}\right] \times \Delta t+\delta_{2}^{t} \\ \delta_{3}^{t+\Delta t} &=\left[a_{3,1} \delta_{3}^{t}+a_{3,2} \delta_{3}^{t-\Delta t}+a_{3,3} \delta_{3}^{t-2 \Delta t}+\cdots+a_{3,10} \delta_{3}^{t} \delta_{3}^{t-\Delta t} \delta_{3}^{t-2 \Delta t}\right] \times \Delta t+\delta_{3}^{t} \end{aligned}\right. $ | (12) |
式中,ε0t+Δt、ε0t, ε0t-Δt、ε0t-2Δt分别为t+Δt、t、t-Δt, t-2Δt时刻的第1个河段的上断面入流误差,a0, 1、a0, 2、a0, 3、…、a0, 10分别为反演方程的参数;δ1t+Δt、δ2t+Δt、δ3t+Δt,δ1t、δ2t、δ3t,δ1t-Δt、δ2t-Δt、δ3t-Δt,δ1t-2Δt、δ2t-2Δt、δ3t-2Δt分别为t+Δt、t、t-Δt, t-2Δt时刻的3个河段的区间入流误差系列,a1, 1、a1, 2、a1, 3、…、a1, 10,a2, 1、a2, 2、a2, 3、…、a2, 10,a3, 1、a3, 2、a3, 3、…、a3, 10均为反演方程的参数.
1.3.3 多河段流量预报误差联合校正将式(12)代入式(10),建立基于马斯京根法矩阵方程的流量预报误差演算方程:
| $ \left[\begin{array}{cccc} 1 & & & \\ -C_{0} & 1 & & \\ & -C_{0} & 1 & \\ & & -C_{0} & 1 \end{array}\right]\left[\begin{array}{l} Q_{0}^{t+\Delta t^{\prime}} \\ Q_{1}^{t+\Delta t^{\prime}} \\ Q_{2}^{t+\Delta t^{\prime}} \\ Q_{3}^{t+\Delta t^{\prime}} \end{array}\right]=\left[\begin{array}{cccc} 0 & & & \\ C_{1} & C_{2} & & \\ & C_{1} & C_{2} & \\ & & C_{1} & C_{2} \end{array}\right]\left[\begin{array}{c} Q_{0, \mathrm{m}}^{t} \\ Q_{1, \mathrm{m}}^{t} \\ Q_{2, \mathrm{m}}^{t} \\ Q_{3, \mathrm{m}}^{t} \end{array}\right]+\left[\begin{array}{c} Q_{0, \mathrm{c}}^{t+\Delta t}+\varepsilon_{0}^{t+\Delta t} \\ q_{1, \mathrm{c}}^{t+\Delta t}+\delta_{1}^{t+\Delta t} \\ q_{2, \mathrm{c}}^{t+\Delta t}+\delta_{2}^{t+\Delta t} \\ q_{3, \mathrm{c}}^{t+\Delta t}+\delta_{3}^{t+\Delta t} \end{array}\right] $ | (13) |
式中,Q0t+Δt′为校正后的t+Δt时刻的第1个河段上断面入流预报值,Q1t+Δt′、Q2t+Δt′、Q3t+Δt′分别为校正后的t+Δt时刻的3个河段下断面出流预报值系列;Q0, mt为t时刻的第1个河段上断面入流实测值,Q1,mt、Q2, mt、Q3, mt分别为t时刻的3个河段下断面出流实测值系列;Q0, ct+Δt为校正前的t+Δt时刻的第1个河段上断面入流预报值,q1, ct+Δt、q2, ct+Δt、q3, ct+Δt分别为校正前的t+Δt时刻的3个河段下断面出流预报值系列;ε0t+Δt、δ1t+Δt、δ2t+Δt、δ3t+Δt分别为t+Δt时刻的流量预报误差系列;C0、C1、C2分别为马斯京根法演算系数.
对式(13)左端第一个矩阵求逆矩阵,然后等式两边左乘这个逆矩阵,整理后得到:
| $ \left[\begin{array}{c} Q_{0}^{t+\Delta t^{\prime}} \\ Q_{1}^{t+\Delta t^{\prime}} \\ Q_{2}^{t+\Delta t^{\prime}} \\ Q_{3}^{t+\Delta t^{\prime}} \end{array}\right]=\left(\mathrm{A}^{\mathrm{T}} \mathrm{A}\right)^{-1} \mathrm{~A}^{\mathrm{T}} \mathrm{B} \times\left[\begin{array}{c} Q_{0, \mathrm{m}}^{t} \\ Q_{1, \mathrm{m}}^{t} \\ Q_{2, \mathrm{m}}^{t} \\ Q_{3, \mathrm{m}}^{t} \end{array}\right]+\left(\mathrm{A}^{\mathrm{T}} \mathrm{A}\right)^{-1} \mathrm{~A}^{\mathrm{T}} \times\left[\begin{array}{c} Q_{0, \mathrm{c}}^{t+\Delta t}+\varepsilon_{0}^{t+\Delta t} \\ q_{1, \mathrm{c}}^{t+\Delta t}+\delta_{1}^{t+\Delta t} \\ q_{2, \mathrm{c}}^{t+\Delta t}+\delta_{2}^{t+\Delta t} \\ q_{3, \mathrm{c}}^{t+\Delta t}+\delta_{3}^{t+\Delta t} \end{array}\right] $ | (14) |
其中:
| $ \mathrm{A}=\left[\begin{array}{cccc} 1 & & & \\ -C_{0} & 1 & & \\ & -C_{0} & 1 & \\ & & -C_{0} & 1 \end{array}\right] $ | (15) |
| $ \mathrm{B}=\left[\begin{array}{cccc} 0 & & & \\ C_{1} & C_{2} & & \\ & C_{1} & C_{2} & \\ & & C_{1} & C_{2} \end{array}\right] $ | (16) |
式(14)写成向量形式如下:
| $ Q(t+\Delta t)=\mathrm{H} Q(t)+\mathrm{P}[q(t+\Delta t)+\varepsilon(t+\Delta t)] $ | (17) |
式中,Η=(ΑΤΑ)-1ΑΤΒ和Ρ=(ΑΤΑ)-1ΑΤ均为系数矩阵,Q(t+Δt)为t+Δt时刻断面流量预报值向量,Q(t)为t时刻断面流量实测值向量,q(t+Δt)为t+Δt时刻区间流量预报值向量,ε(t+Δt)为t+Δt时刻区间流量预报误差预测值向量.
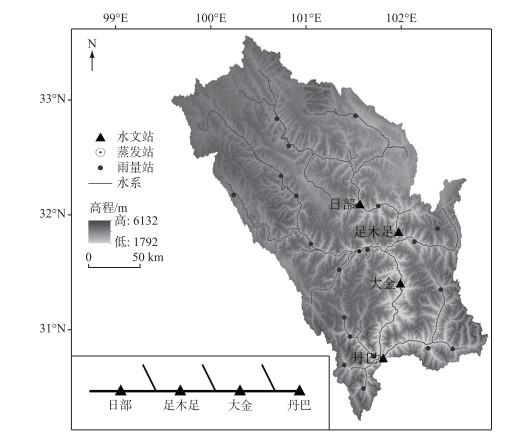
2 应用与分析 2.1 研究区域及资料大渡河是中国长江支流岷江的正源,丹巴水文站是大渡河上游的一个重要节点. 丹巴站以上流域年平均降水量为600~700 mm,年平均径流量为400~500 mm,流域控制面积为52763 km2,约占大渡河流域总面积的68 %. 丹巴站径流的变化可以直接反映大渡河上游区的流量变化,也可以决定下游区的来水变化. 因此,保证丹巴站获得精准的洪水预报意义重大. 由于丹巴站以上流域的地形地质条件复杂,河道迂回曲折,支流较多,且站点布设困难,雨量站网密度稀疏,因而难以准确描绘该流域的下垫面机制,难以测得流域的面降雨量和各河道断面和区间的流量,这些都导致在丹巴站的洪水预报不准确. 但丹巴站以上流域内有不少水文测站,可基于站点信息,采用本文提出的多河段联合校正方法对预报洪水进行校正.
图 2所示为丹巴站以上流域的地理位置、河系概况及测站分布. 对该流域内的河道、支流、站点分布等进行合理概化. 概化后以丹巴水文站为研究站点,以丹巴站以上河流系统为研究河道,在干流选取4个代表性水文站(日部、足木足、大金、丹巴),将长河段划分为3个子河段(日部—足木足、足木足—大金、大金—丹巴),对本文方法进行应用检验. 根据该流域2009—2016年的水文气象观测数据对各站点进行流量预报. 根据河道洪水传播特性,预报时间步长Δt取24 h. 根据已有研究成果[20],确定采用的马法参数为:x=0.4,K=25,C0=0.074,C1=0.815,C2=0.111. 选用8场洪水资料对各河段入流误差的反演方程参数进行率定和检验,其中4场用于率定,4场进行验证,参数率定结果见表 1.
|
图 2 大渡河丹巴站以上河流系统 Fig.2 River system of Dadu River above Danba station |
| 表 1 各河段入流误差的反演方程系数向量的率定结果 Tab. 1 Calibration results of the coefficient vectors of the inversion equations for the inflow errors of each reach |
本文采用4个基本指标[21-22]来定量描述洪水预报的精度,并借助2个统计指标来比对各校正方法的误差修正能力. 各评价指标的计算公式和符号含义如下:
1) 洪峰流量相对误差:
| $ {\rm{ \mathsf{ δ} }} Q_{\mathrm{m}}=\left[\left(Q_{\mathrm{m}, \mathrm{obs}}-Q_{\mathrm{m}, \mathrm{c}}\right) / Q_{\mathrm{m}, \mathrm{obs}}\right] \times 100 \% $ | (18) |
式中,Qm, obs为实测洪峰流量(m3/s), Qm, c为预报洪峰流量(m3/s);δQm为洪峰流量相对误差.
2) 峰现时间绝对误差:
| $ \Delta T=T_{Q_{\mathrm{m,obs}}}-T_{Q_{\mathrm{m}, \mathrm{c}}} $ | (19) |
式中,TQm, obs为实测峰现时间(h), TQm, c为预报峰现时间(h), ΔT为峰现时间绝对误差(h).
3) 径流深相对误差:
| $ {\rm{ \mathsf{ δ} }} R=\left[\left(R_{\mathrm{obs}}-R_{\mathrm{c}}\right) / R_{\mathrm{obs}}\right] \times 100 \% $ | (20) |
式中,Robs为实测次洪径流深(mm), Rc为预报次洪径流深(mm), δR为径流深相对误差.
4) 确定性系数:
| $ D_{C}=1-\sum\limits_{t=1}^{n}\left[Q_{\mathrm{obs}}(t)-Q_{\mathrm{c}}(t)\right]^{2} / \sum\limits_{t=1}^{n}\left[Q_{\mathrm{obs}}(t)-\bar{Q}_{\mathrm{obs}}\right]^{2} $ | (21) |
式中,Qobs(t)为t时刻的洪水实测流量(m3/s);Qc(t)为t时刻的洪水预报流量(m3/s);Qobs为n个时段的实测流量均值(m3/s);DC为洪水预报过程与实测过程之间的确定性系数.
5) 为了比较不同次洪间多指标综合效果,将(1)~(4)的评价指标平均值进行归一化处理.
确定性系数的归一化算法为:
| $ D_{C}^{*}=\frac{D_{C}-D_{C, \min }}{D_{C, \max }-D_{C, \min }} $ | (22) |
式中,DC为归一化处理前的确定性系数,DC, min为确定性系数的全局最小值,DC, max为确定性系数的全局最大值,DC*为归一化处理后的确定性系数.
其余指标的归一化算法为:
| $ W^{*}=\frac{W_{\max }-W}{W_{\max }-W_{\min }} $ | (23) |
式中,W为归一化处理前的指标值,Wmin为指标的全局最小值,Wmax为指标的全局最大值,W*为归一化处理后的指标值.
不同的评价指标具有不同的量纲和量纲单位,因此不具有可比性. 若要综合比较不同条件下的不同指标,需要对指标进行归一化处理,以消除指标之间的量纲影响. 归一化后的各评价指标处于同一量级,适合进行综合评价(comprehensive evaluation, CE)[23]. 一般采用雷达图的图形数值相结合的方式来综合展示所有归一化指标的对比结果. 在雷达图中,单个归一化指标数值越大,越接近1,表示模拟效果越好;对于不同方法的多个归一化指标,雷达图所围面积越大,表示该方法模拟效果越好.
6) 为了比较不同校正方法对预报误差的修正效果,计算基准系数BE[21, 24]:
| $ B_{\mathrm{E}}=1-\sum\limits_{t=1}^{n}\left[Q_{\mathrm{obs}}(t)-Q_{\mathrm{c}}(t)\right]^{2} / \sum\limits_{i=1}^{n}\left[Q_{\mathrm{obs}}(t)-Q_{\mathrm{b}}(t)\right]^{2} $ | (24) |
式中,Qb(t)为t时刻的基准预报流量(m3/s);其它变量含义同上.
不同校正方法对原始基准预报的提升效果不一样,基准系数可用来评价校正前后的预报精度提升程度和校正方法的相对好坏. BE≤0,表示校正后的预报结果表现较差,校正方法不可取;BE>0,表示校正结果较优,且BE越大,校正效果越明显.
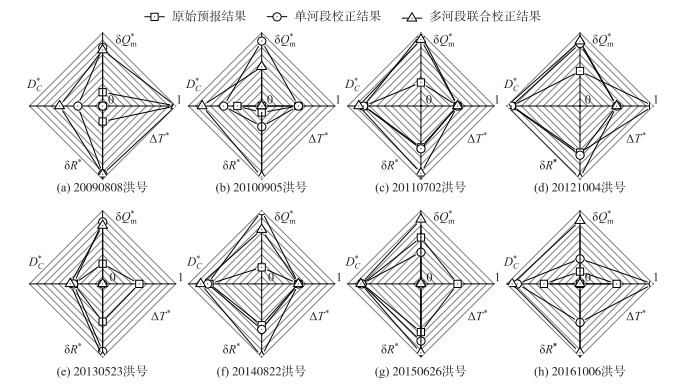
2.3 结果分析及讨论本文利用大渡河丹巴水文站以上流域的各实测洪水系列资料作为实例研究,考察多河段联合校正模型的误差修正效果. 将丹巴站以上河流系统的1个长河段划分成3个短河段,利用丹巴站的8场次洪实测资料,进行河道洪水的预报与校正,采用归一化指标δQm*、ΔT*、δR*和DC*量化原始预报值、单河段校正预报值、以及多河段联合校正预报值,绘制成雷达图进行综合分析. 其中,“原始预报值”是直接通过新安江模型进行洪水预报、未经过误差校正的结果,“单河段校正预报值”是根据1.2节中的马斯京根流量演算单河段校正模型进行预报误差校正后的结果,“多河段联合校正预报值”是根据本文提出的多河段联合校正模型进行预报误差校正后的结果.
从图 3中可以看出:①多河段联合校正模型的雷达图所围面积明显大于原始预报的雷达图所围面积,甚至多河段联合校正模型的雷达图能完全覆盖原始预报的雷达图. 由此可见,多河段联合校正模型对不同年份、不同时期、不同量级的洪水进行预报误差校正时,均能有效地提升洪水预报精度,且提升效果明显. ②对每场洪水预报值的校正,多河段联合校正模型的雷达图所围范围均比单河段校正模型的雷达图所围范围更大. 由此可知,多河段联合校正模型的误差修正效果,可能有时在个别评价指标上不如单河段校正模型,但在整体上是优于单河段校正模型的. ③对于4个归一化指标,多河段联合校正模型的指标δQm*、δR*和DC*基本都接近于1,单河段校正模型只有指标δQm*基本接近于1. 由此发现,两种校正模型对洪峰流量的误差修正能力相当,但多河段联合校正模型对洪量和整个洪水过程的误差修正能力更为突出. 分析其原因,是由于多河段联合校正模型充分考虑了各河段和区间误差,能及时并准确地调整整个河道汇流过程,所以不仅能把握住出口断面处的峰值预报,还能做好整个洪水过程的非峰值预报.
|
图 3 8场次洪统计指标雷达图 Fig.3 Radar chart of statistical indicators of eight floods |
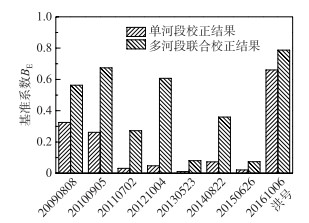
图 4提供了8场次洪的基准系数BE的对比. 从图 4中可以看出:①多河段联合校正模型和单河段校正模型的所有BE全部大于0,2种校正方法对所有场次洪水过程的预报值都有提升,提升率为100 %. ②多河段联合校正模型比单河段校正模型的提升效果更明显,基准系数能多提升0.1以上. ③多河段联合校正模型不仅能提高所有场次洪水的预报效果,还能稳定地提升至一个较高的精度,最低的BE为0.08,最高的BE达0.79. 由此可推断,随着划分的河段数目增加(如:丹巴站以上河道从单段/1段划分成3段),利用的断面和区间资料信息增多,则根据误差反演措施所带来的校正模型的误差修正作用增强. 相当于每增加一个水文测站,河道上就增加一个误差“传感器”,河道划分越精细,“传感器”越多. “传感器”可以及时地发现误差在什么地方什么时刻出现、误差有多大,校正模型就能据此进行必要的误差修正. 所以,出口断面受上游不确定性影响减弱,最终预报结果的精度提高.
|
图 4 2种校正方法的基准系数对比 Fig.4 Comparison of Benchmark coefficients of two calibration methods |
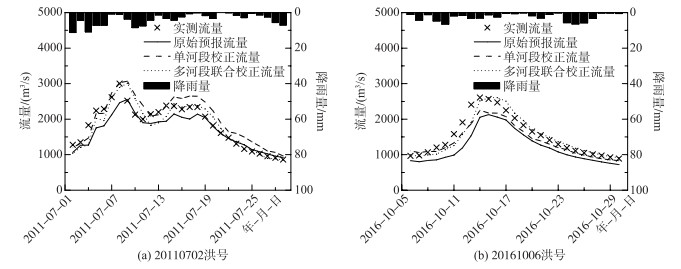
选取8场洪水中的第20110702号和第20161006号洪水作为示例,查看误差修正效果. 图 5显示了这2场洪水校正前后的预报流量对比,图 5a为丹巴水文站的2011年7月2日发生的洪水,图 5b为2016年10月6日发生的洪水. 从图 5中可以看出:① 2种校正模型均能有效地校正洪水原始预报结果,将2场不合格的洪水预报变为合格的预报. ②相较而言,多河段联合校正模型综合表现最佳,不论对洪峰还是洪水过程的校正,效果更为理想,这有利于在实际应用中,准确地模拟流量过程线,尤其是捕捉峰值,以降低洪水风险. ③多河段联合校正模型对单峰洪水(如20161006号洪水)和复峰洪水(如20110702号洪水)的预报误差的校正效果相当. 结果在一定程度上说明,本文提出的基于误差反演的多河段联合校正模型,将各河段洪水预报误差演算,并联合进行误差校正的做法更为合理,可进一步提高流域出口断面的洪水预报精度.
|
图 5 两场次洪的预报及校正结果 Fig.5 Forecast and correction results of two floods |
1) 本研究将马斯京根矩阵方程和动力系统反演方程相结合,提出洪水预报误差反演的多河段联合校正方法. 该方法考虑了复杂河系中各断面在空间上的水力联系和预报误差在时程上的传递规律,充分利用上游多断面实测和校正信息对下游预报断面的预报误差进行校正. 该方法物理意义明确,理论先进.
2) 在大渡河流域的应用结果表明,对不同年月发生的场次洪水均能取得稳定有效的校正效果,显著提升洪水预报精度. 相比于单河段校正方法,多河段联合校正方法在校正能力上整体更优,能保证洪峰、洪量及整个洪水过程的预报精度.
3) 本文对大渡河流域构建的洪水预报误差反演方程属于三元三次项的非线性模型,对其它流域未必适合,但文中采用的方法具有普适性,可根据应用流域的实际误差传递规律进行优化调整,以获得更好的校正效果. 因此,本文方法也受限于洪水预报能力和误差多时段外延效果,需进一步拓展研究.
| [1] |
Liu GW. Definition and classification of non-structure measures for flood prevention. Advances in Water Science, 2003, 14(1): 98-103. [刘国纬. 论防洪减灾非工程措施的定义与分类. 水科学进展, 2003, 14(1): 98-103. DOI:10.3321/j.issn:1001-6791.2003.01.017] |
| [2] |
Ge SX ed. Modern flood forecasting techniques. Beijing: China Water Power Press, 1999. [葛守西. 现代洪水预报技术. 北京: 中国水利水电出版社, 1999.]
|
| [3] |
Bao WM, Zhang JY ed. Hydrological forecast: 4rd edition. Beijing: China Water Resources and Hydropower Press, 2009. [包为民, 张建云. 水文预报: 第4版. 北京: 中国水利水电出版社, 2009.]
|
| [4] |
Zhang JY. Review and reflection on China's hydrological forecasting techniques. Advances in Water Science, 2010, 21(4): 435-443. [张建云. 中国水文预报技术发展的回顾与思考. 水科学进展, 2010, 21(4): 435-443.] |
| [5] |
Liu GW. Basic problems and frontier of hydrology. Advances in Water Science, 2020, 31(5): 685-689. [刘国纬. 水文科学的基本问题及当代前沿. 水科学进展, 2020, 31(5): 685-689.] |
| [6] |
Huang YX, Wang QZ, Liang ZM et al. Research advances on real-time correction methods for flood forecasting. South-to-North Water Transfers and Water Science & Technology, 2021, 19(1): 1-21. [黄一昕, 王钦钊, 梁忠民等. 洪水预报实时校正技术研究进展. 南水北调与水利科技, 2021, 19(1): 1-21.] |
| [7] |
Yang RX, Hou BD, Xiao WH et al. The applicability of real-time flood forecasting correction techniques coupled with the Muskingum method. Hydrology Research, 2020, 51(1): 17-29. DOI:10.2166/nh.2019.128 |
| [8] |
Si W, Bao WM, Qu SM et al. Real-time flood forecast updating method based on mean areal rainfall error correction. J Lake Sci, 2018, 30(2): 533-541. [司伟, 包为民, 瞿思敏等. 基于面平均雨量误差修正的实时洪水预报修正方法. 湖泊科学, 2018, 30(2): 533-541. DOI:10.18307/2018.0224] |
| [9] |
Si W, Gupta HV, Bao WM et al. Improved dynamic system response curve method for real-time flood forecast updating. Water Resources Research, 2019, 55(9): 7493-7519. DOI:10.1029/2019wr025520 |
| [10] |
Wang CH, Wu XL, Zhou Q. Application of Kalman filter technique in real-time flood forecasting. Journal of Hohai University: Natural Sciences, 2008, 36(3): 300-305. [王船海, 吴晓玲, 周全. 卡尔曼滤波校正技术在水动力学模型实时洪水预报中的应用. 河海大学学报: 自然科学版, 2008, 36(3): 300-305. DOI:10.3876/j.issn.1000-1980.2008.03.003] |
| [11] |
Chang L, Liu KL, Yao C et al. Real-time flood forecasting system for complicated river channels: A case study from Wangjiaba to Xiaoliuxiang section in the Huaihe River basin. J Lake Sci, 2013, 25(3): 422-427. [常露, 刘开磊, 姚成等. 复杂河道洪水预报系统研究——以淮河王家坝至小柳巷区间流域为例. 湖泊科学, 2013, 25(3): 422-427. DOI:10.18307/2013.0317] |
| [12] |
Xu XY, Fang HW, Zhang YF et al. A real-time probabilistic channel flood forecasting model and application based on particle filters. Advances in Water Science, 2015, 26(3): 356-364. [徐兴亚, 方红卫, 张岳峰等. 河道洪水实时概率预报模型与应用. 水科学进展, 2015, 26(3): 356-364.] |
| [13] |
Gao YH, Zhong PA, Xu B et al. Study on multi-point joint correction method for real-time flood forecasting errors of river systems. South-to-North Water Transfers and Water Science & Technology, 2018, 16(5): 21-26. [高益辉, 钟平安, 徐斌等. 河流系统实时洪水预报误差多点联合校正方法研究. 南水北调与水利科技, 2018, 16(5): 21-26.] |
| [14] |
Liang ZM, Wang XW, Ning YW et al. Study on error correction method of Muskingum flow calculation based on dynamic system inversion theory. Water Power, 2017, 43(12): 9-12. [梁忠民, 王旭伟, 宁亚伟等. 基于动力系统反演理论的马斯京根流量演算误差校正. 水力发电, 2017, 43(12): 9-12. DOI:10.3969/j.issn.0559-9342.2017.12.003] |
| [15] |
Zhu H. The matrix equation solution technology of Muskingum method. Journal of China Hydrology, 1987, 7(4): 7-9. [朱华. 马斯京根法的矩阵方程求解法. 水文, 1987, 7(4): 7-9.] |
| [16] |
Huang JP, Yi YH. Inversion of nonlinear dynamic model from observational data. Science in China: Ser B, 1991, 21(3): 331-336. [黄建平, 衣育红. 利用观测资料反演非线性动力模型. 中国科学: B辑, 1991, 21(3): 331-336. DOI:10.3321/j.issn:1006-9240.1991.03.002] |
| [17] |
Ding J, Wang WS, Zhao YL. The exploration on inversion of model for hydrologic dynamic system. Journal of Hydroelectric Engineering, 2002, 21(3): 7-11. [丁晶, 王文圣, 赵永龙. 反演水文动力模型的探讨. 水力发电学报, 2002, 21(3): 7-11. DOI:10.3969/j.issn.1003-1243.2002.03.002] |
| [18] |
Singh VP, McCann RC. Some notes on Muskingum method of flood routing. Journal of Hydrology, 1980, 48(3/4): 343-361. DOI:10.1016/0022-1694(80)90125-0 |
| [19] |
Rui XF, Zhang C. Development and inspiration of Muskingum method. Advances in Science and Technology of Water Resources, 2014, 34(3): 1-6. [芮孝芳, 张超. Muskingum法的发展及启示. 水利水电科技进展, 2014, 34(3): 1-6.] |
| [20] |
Zhang Y, Liang ZM, Chen ZN et al. Study on flood forecast and real-time correction in upper reaches of Dadu River basin. Water Power, 2020, 46(5): 13-15, 21. [张艳, 梁忠民, 陈在妮等. 大渡河流域上游洪水预报及实时校正研究. 水力发电, 2020, 46(5): 13-15, 21.] |
| [21] |
Jiang XL, Liang ZM, Hu YM et al. Research on assessment criteria in probabilistic flood forecasting. J Lake Sci, 2020, 32(2): 539-552. [蒋晓蕾, 梁忠民, 胡义明等. 洪水概率预报评价指标研究. 湖泊科学, 2020, 32(2): 539-552. DOI:10.18307/2020.0222] |
| [22] |
Liang ZM, Huang YX, Hu YM et al. The entire-process correction approach for flood forecasting. South-to-North Water Transfers and Water Science & Technology, 2020, 18(1): 1-10, 17. [梁忠民, 黄一昕, 胡义明等. 全过程联合校正的洪水预报修正方法. 南水北调与水利科技, 2020, 18(1): 1-10, 17.] |
| [23] |
Zheng HL, Liu C, Zhai DN. Comprehensive evaluating method based on radar-graph. Journal of Nanjing Institute of Posts and Telecommunications: Natural Science, 2001, 21(2): 75-79. [郑惠莉, 刘陈, 翟丹妮. 基于雷达图的综合评价方法. 南京邮电学院学报: 自然科学版, 2001, 21(2): 75-79. DOI:10.3969/j.issn.1673-5439.2001.02.015] |
| [24] |
Schaefli B, Gupta HV. Do Nash values have value?. Hydrological Processes, 2007, 21(15): 2075-2080. DOI:10.1002/hyp.6825 |
 2021, Vol. 33
2021, Vol. 33 


