(2: 江苏省太湖水利规划设计研究院有限公司, 苏州 215106)
(3: 江苏省洪泽湖水利工程管理处, 淮安 223100)
(2: Jiangsu Research Institute of Water Conservancy Planning and Design for Lake Taihu Co., Ltd., Suzhou 215106, P. R. China)
(3: Hongze Lake Water Conservancy Project Management Office of Jiangsu Province, Huai'an 223100, P. R. China)
洪泽湖位于江苏省中西部,淮河中下游流域,是我国第四大淡水湖,同时也是淮河防洪和“南水北调”东线工程调蓄湖泊和苏北地区重要的战略水源地,在防洪、供水、灌溉、调水、渔业、航运及生态涵养等方面发挥着重要作用[1-2]. 流场是湖泊中最重要的动力场之一,不仅对湖泊水体温度、盐度和浊度等关键物理要素具有重要影响,同时对湖泊内悬浮物、溶解质和污染物的输移、扩散、转化,以及藻类、浮游动物、水生植被和鱼类等水生态系统要素也具有决定性的影响,一直是湖泊研究的重点方向[3-4]. 因此加强对洪泽湖流场的研究,对于湖泊资源的开发利用和生态环境保护都具有重要意义.
湖泊流场主要由河道出入湖水量驱动形成的吞吐流、湖面风场驱动形成的风生流以及湖泊水体温盐时空变化形成的密度流组成[5]. 对于多数大型浅水湖泊,由于河流入湖流量相对湖泊储水量小得多,因此吞吐流流速除在河流入湖区较大外,在内湖区一般比较微弱. 湖泊水体温盐变化驱动形成的密度流流速更小,几乎达到可忽略的程度[6-7]. 湖泊风生流流场由湖面风场驱动形成,其流速和流向受到湖面风场、水位及湖泊岸线形态、湖底地形以及地球自转等多重要素共同作用[8]. 风生流主要的形成机制为湖泊表层水体受到风应力作用触发水体运动. 随着表层水体运动,在垂向上产生水流流速切变,在水体内部的粘滞力作用下,中下水层产生相对于湖底的运动,但湖底摩擦力会阻碍湖水运动. 湖水在下风方向产生涌水,水位升高,进而在湖泊内形成压力梯度力,压力梯度力方向由高水位指向低水位,因此其方向和风应力方向不同. 在风场作用下湖泊水体承受的作用力不但随位置发生变化,而且随风作用历时变化也发生着变化,导致风生流结构的高度复杂性,其大小和方向呈非稳定状态. 另外湖面风场存在空间和时间的快速变化,湖泊流场大小呈现较大的随机性和偶然性,其观测和特征提取十分困难[5, 9]. 到目前为止,虽然国内外对湖泊风生流已开展了大量研究[10-12],但对于不同湖泊风生流的结构时空变化规律的认识仍然处于碎片化的状态[8].
湖泊风生流研究主要有现场观测、实验室物模及数值模拟等方法. 数值模拟方法由于可以全方位、高时空分辨率的认识风生流在不同水文、气象和地形要素驱动下时空演化特征,已经成为风生流研究的重要方法[13-14]. 目前针对洪泽湖流场风生流数值模拟最早的参考文献可追述到1996年,姜加虎等[15]利用二维水动力模型模拟了10.0 m/s定常风下洪泽湖风生流特征,结果表明洪泽湖在同风速但反风向的风场驱动下风生流流态相近,但流向相反;刘翊竣等[16]利用MIKE21模型模拟了东南风作用下洪泽湖风生流特征,研究认为风速变化会改变流速,但不会改变流场结构. 上述研究为认知洪泽湖风生流特征奠定了基础. 但现有研究主要基于二维水动力模型开展,彭兆亮等[17]和张怡辉等[18]通过现场观测研究结果表明,洪泽湖流场结构存在明显垂向差异,在某些水文气象条件驱动下,局部湖区出现表层水体与底层水体流向完全相反的特征. 因此需要建立三维数值模型全方位地揭示洪泽湖在不同风场驱动下的水平和垂向空间湖流分布特征. 此外,现有研究并未利用实测湖流数据验证模型对湖流的模拟精度,因此无法判断结论的可靠程度. 另外一方面,湖泊水位波动也是影响湖泊流场的重要因素,水位的变化导致水体不同深度处斜压结构的变化,进而会引发不同水层流速及流向的改变[5, 19]. 但目前国内外关于水位变化对湖泊风生流影响的数值研究仍然十分薄弱.
本文的主要目的是在建立洪泽湖三维水动力模型,并利用实测湖流数据验证模型的基础上,基于长系列风场监测数据确定洪泽湖不同月份及全年风速风向特征,全面开展不同风速、风向和水位驱动下的洪泽湖风生流数值试验,分析全湖及分湖区水平及垂向空间风生流对于风速、风向和水位变化的响应特征,为洪泽湖资源与生态环境保护提供理论基础.
1 数据与方法 1.1 研究区概况洪泽湖(图 1)为淮河过水湖泊,水位和湖面面积变幅较大,平均水深仅为1.9 m. 根据湖泊形态,洪泽湖可划分为溧河洼、成子湖、洪泽湖主体及南部湖区4个湖区. 洪泽湖多年平均气温为19.9℃,7月平均气温最高,为27.8℃;1月平均气温最低,为1.6℃,多年平均年降水量为964.1 mm. 受季风影响,雨季集中在6—9月,降水量占全年的65.9 %;受北方寒冷气团的影响,冬季降水量较少,仅占7 % ~8 %. 洪泽湖主要入湖河流有淮河、徐洪河、新汴河、怀洪新河、濉河、城子河等,多分布于洪泽湖的西岸. 主要出湖河道为三河、淮沭河和苏北灌溉总渠[1-2].
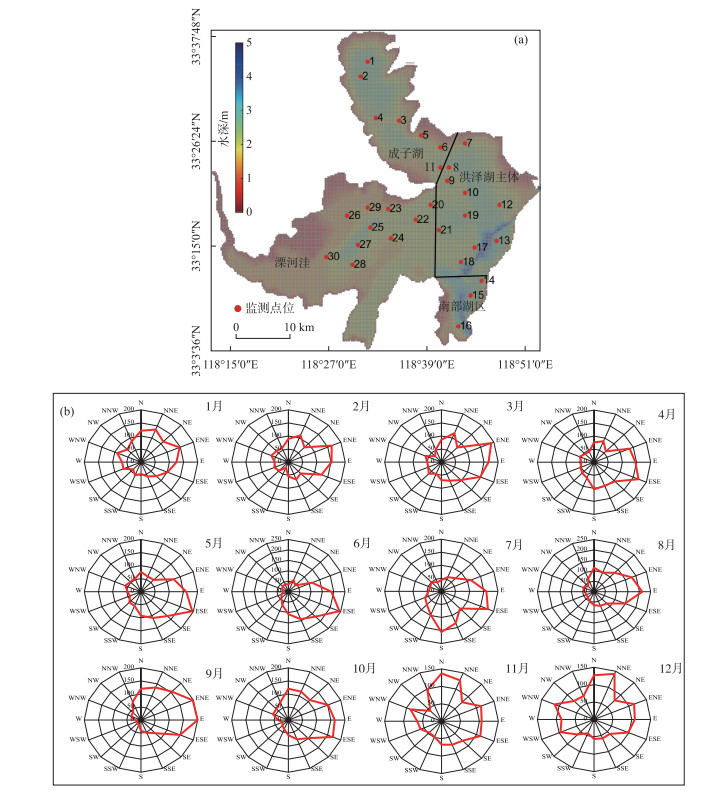
|
图 1 洪泽湖水下地形、湖流监测点位、湖区划分(黑线)与水动力模型计算单元(a);1975—2020年泗洪站各月风向玫瑰图(b) Fig.1 Bathymetry map of Lake Hongze with indication of sampling sites, lake-basin division (black curves) and numerical modelling grid cells (a); rose plots of monthly wind directions derived from observations at Sihong Meteorological Station during 1975-2020 (b) |
为研究洪泽湖在不同出入湖流量和风场作用下的三维湖流特征,并验证水动力模型精度,分别于2020年8月4日和11月2日开展了全湖30个点位流场观测. 所用仪器为Sontek River Surveyor M9型声学多普勒剖面仪(ADP)系统. 该仪器对于水体流速测量范围为0~30 m/s,测量误差为流速的±1 % 范围之内. 为尽可能获取不同湖区湖流同步观测数据,每次调查分为3个小组分湖区开展. 乘坐快艇到达调查点位后,进行仪器各部件的组装,利用笔记本电脑预装的仪器软件进行监测参数配置. 为补偿不同测量地点的磁场对仪器内罗盘的影响,每次测量前先进行罗盘校正,启动仪器开始对水深以及不同水深处南北向、东西向和垂向三维流速的观测,每个点位持续观测15 min以上. 在开展湖流监测的同时,利用手持式风速风向仪测量现场风场情况.
收集了2014—2020年较为完整的洪泽湖主要出入湖口门逐日流量与湖区水位等水文数据,以及逐时气象数据. 水文数据来源于洪泽湖水利工程管理处,包括淮河、怀洪新河、新汴河、濉河、老濉河、徐洪河和池河等入湖河道流量数据,以及三河、三河引河、淮沭河、苏北灌溉总渠、南水北调洪泽湖电站以及洪金洞、周桥洞等出湖河道及闸坝流量数据. 洪泽湖水位监测数据包括老子山、蒋坝、高良涧及尚嘴4个站点. 气象数据来源于国家气象数据共享网,使用泗洪基本站风速、风向数据,其中1975年1月—2016年8月为逐日数据,2016年8月—2020年10月为逐时数据. 1975—2020年洪泽湖泗洪站各月风向玫瑰图如图 1b所示.
1.3 洪泽湖三维水动力模型构建基于三维水动力富营养化生态模型Ecolake模型[20-24]的水动力模块构建洪泽湖三维水动力模型. 在笛卡尔坐标系下,洪泽湖湖水三维运动控制方程可以表示为:
| $ \begin{gathered} \frac{\partial(H u)}{\partial x}+\frac{\partial(H v)}{\partial y}+\frac{\partial\left(H w^{*}\right)}{\partial \sigma}+\frac{\partial \zeta}{\partial t}=0 \end{gathered} $ | (1) |
| $ \begin{gathered} \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}+w^{*} \frac{\partial u}{\partial \sigma}-f v=-g \frac{\partial \zeta}{\partial x}+A_{v}\left(\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}\right)+\frac{\partial}{\partial \sigma}\left(A_{z} \frac{\partial u}{\partial \sigma}\right)+\varepsilon_{x} \end{gathered} $ | (2) |
| $ \begin{gathered} \frac{\partial v}{\partial t}+u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}+w^{*} \frac{\partial v}{\partial \sigma}+f u=-g \frac{\partial \zeta}{\partial y}+A_{v}\left(\frac{\partial^{2} v}{\partial x^{2}}+\frac{\partial^{2} v}{\partial y^{2}}\right)+\frac{\partial}{\partial \sigma}\left(A_{z} \frac{\partial v}{\partial \sigma}\right)+\varepsilon_{y} \end{gathered} $ | (3) |
式中, x、y分别为x、y轴坐标;u、v分别为x、y方向流速;t为时间;f为科氏力参数;g为重力加速度;h为水面平衡位置到湖底的距离;H为湖面到湖底的水深;ζ为水面离开平衡位置的位移;εx、εy分别为x、y方向控制方程水平扩散项因变换产生的偏差项;w*为σ方向速度,它和垂直方向速度w的关系如下:
| $ w=H \cdot w^{*}+\sigma\left(\frac{\partial \zeta}{\partial t}+u \frac{\partial \zeta}{\partial x}+v \frac{\partial \zeta}{\partial y}\right)-(1-\sigma)\left(u \frac{\partial h}{\partial x}+v \frac{\partial h}{\partial y}\right) $ | (4) |
εx表达式为:
| $ \begin{array}{r} \varepsilon_{x}=A_{h}\left\{\frac{2}{H} \frac{\partial^{2} u}{\partial x \partial \sigma}\left(\frac{\partial h}{\partial x}-\sigma \frac{\partial H}{\partial x}\right)+\frac{\partial^{2} u}{\partial \sigma^{2}} \frac{1}{H^{2}}\left(\frac{\partial h}{\partial x}-\sigma \frac{\partial H}{\partial x}\right)^{2}-2 \frac{\partial u}{\partial \sigma} \frac{1}{H^{2}} \frac{\partial H}{\partial x}\left(\frac{\partial h}{\partial x}-\sigma \frac{\partial H}{\partial x}\right)+\right. \\ \frac{\partial u}{\partial \sigma} \frac{1}{H}\left(\frac{\partial^{2} h}{\partial x^{2}}-\sigma \frac{\partial^{2} H}{\partial x^{2}}\right)+\frac{2}{H} \frac{\partial^{2} u}{\partial y \partial \sigma}\left(\frac{\partial h}{\partial y}-\sigma \frac{\partial H}{\partial y}\right)+\frac{\partial^{2} u}{\partial \sigma^{2}} \frac{1}{H^{2}}\left(\frac{\partial h}{\partial y}-\sigma \frac{\partial H}{\partial y}\right)^{2}- \\ \left.2 \frac{\partial u}{\partial \sigma} \frac{1}{H^{2}} \frac{\partial H}{\partial y}\left(\frac{\partial h}{\partial y}-\sigma \frac{\partial H}{\partial y}\right)+\frac{\partial u}{\partial \sigma} \frac{1}{H}\left(\frac{\partial^{2} h}{\partial y^{2}}-\sigma \frac{\partial^{2} H}{\partial y^{2}}\right)\right\} \end{array} $ | (5) |
εy的表达式与εx的表达式相同,只需把u换成v即可.
在σ坐标系下,上边界条件为:
| $ \begin{array}{l} \sigma=1: \ \ \ \ \ \ w^{*}=0 \\ \qquad\qquad\qquad\qquad \rho \frac{A v}{H}\left(\frac{\partial u}{\partial \sigma}, \frac{\partial v}{\partial \sigma}\right)=\left(\tau_{x}^{s}, \tau_{y}^{s}\right)=C_{D}^{s} \rho a \sqrt{u_{a}^{2}+v_{a}^{2}}\left(u_{a}, v_{a}\right) \end{array} $ | (6) |
| $ \begin{array}{l} \sigma=0: \ \ \ \ \ \ w^{*}=0 \\ \qquad\qquad\qquad\qquad \frac{A v}{H}\left(\frac{\partial u}{\partial \sigma}, \frac{\partial v}{\partial \sigma}\right)=\left(\tau_{x}^{b}, \tau_{y}^{b}\right)=C_{D}^{b} \rho a \sqrt{u_{b}^{2}+v_{b}^{2}}\left(u_{b}, v_{b}\right) \end{array} $ | (7) |
式中, ua、va、ub、vb分别为风速、湖底流速x、y方向的分量、CDs、CDb分别为风、湖底拖曳系数,流速方程的侧边界条件为法向速度为零.
1.4 模型设置与验证采用正交网格对洪泽湖计算单元进行空间划分,网格东西向、南北向步长为250 m,全湖水平空间共划分为约2.8万个计算单元(图 1a). 根据模型数值计算的收敛条件,模型计算时间步长设置为15 s,计算结果按小时尺度输出. 从水面至湖底把垂直水柱划分5个厚度一致的水层:风应力控制区(表层)、风应力至水平压强梯度力控制过渡区(次表层)、水平压强梯度力控制区(中间层)、水平压强梯度力与底摩擦力联合控制区(次底层)与底摩擦力控制区(底层),各层的厚度与水深同步变化.
洪泽湖环湖河道众多,将洪泽湖所有出入湖河道概化为汴河、成子河、高桥河、高松河、淮河、淮洪新河、淮沭河、淮泗河、黄码河、老三河、利民河、马化河、三河、维桥河、五河、肖河、新汴河、新濉河、赵公河、入海水道高良涧闸等24条出入湖河道.
由于湖泊流场为矢量,既包括水体流动速率,又含有方向信息,传统的标量评价方法,如纳什系数、确定性系数等指标无法直接评价模型对湖流的模拟精度. 因此,使用归一化傅里叶范数[7, 25](normalized fourier norm, Fn)来验证水动力模型对于洪泽湖流场的模拟精度. Fn可用下式计算得到:
| $ F n=\left(\sqrt{\frac{1}{T} \sum\limits_{i=1}^{T}\left|\overrightarrow{V_{\text {sim }}}-\overrightarrow{V_{\text {obs }}}\right|^{2}}\right) / \sqrt{\frac{1}{T} \sum\limits_{t=1}^{T}\left|\overrightarrow{V_{\mathrm{obs}}}\right|^{2}} $ | (8) |
式中, Fn为归一化傅里叶范数,可理解为湖流的模拟值和实测值向量之间的差值的模与观测向量的模之间的比值;
洪泽湖水动力模型采用零速启动方式运行,因此模型需要提前预热7 d左右. 经过预热,初值对于模型计算结果的影响被耗散掉,模型的状态变量达到稳定. 因此从2020年7月28日开始运行模型,采用连续计算的方式运行至11月2日结束. 在此期间,洪泽湖气温在2.9~36.7℃之间波动,平均气温为22.5℃,降水总量为390 mm, 风速在0~5.8 m/s之间波动,以东风风向为主,洪泽湖老子山、蒋坝、高良涧和尚嘴4站日平均水位在12.72~13.81 m之间波动.
1.5 风生流模拟情景设计与情景数值试验由于缺少系统的洪泽湖湖区风场监测资料,利用泗洪国家气象基本站1975年1月至2020年9月逐日风速风向监测数据,统计各月北风、北偏东、东北等16种风向出现的频率百分比并绘制各月风向玫瑰图,确定洪泽湖典型风速风向. 以此为基础,开展风速、风向和水位变化对风生流影响的数值模拟.
1) 风场变化对洪泽湖风生流影响模拟. 为全面分析不同风向驱动下洪泽湖三维风生流特征,模拟洪泽湖平均风速和12.5 m保证水位条件下,湖面风向分别为北风、北偏东风、东北风等16种不同风向下洪泽湖垂向平均以及表层、次表层、中间层、次底层和底层各层流场分布特征.
2) 风速变化对洪泽湖风生流影响模拟. 为分析风速变化对洪泽湖风生流影响,模拟洪泽湖保证水位,典型风向、不同风速条件下洪泽湖4个湖区垂向平均及垂向各层平均流速变化.
3) 水位变化对洪泽湖风生流影响模拟. 为了进一步探究水位变化对洪泽湖风生流影响,模拟典型风速风向驱动下,不同初始水位下洪泽湖三维风生流变化情况.
2 结果与讨论 2.1 三维水动力生态模型验证首先分析洪泽湖水动力模型对湖流模拟的精度. 图 2左列显示了模型对于2020年8月4日全湖表层、中层和底层流场模拟结果,其中左侧最上方子图显示了30个监测点位的具体位置;右列对比了各点位表层、中层和底层流场模拟值与对应时刻的监测值. 由于模型水平空间分辨率为250 m, 全湖水平空间计算单元数接近3万个,流场分布图无法显示所有网格,因此计算并显示1 km范围内16个网格的平均东西向和南北向流速.
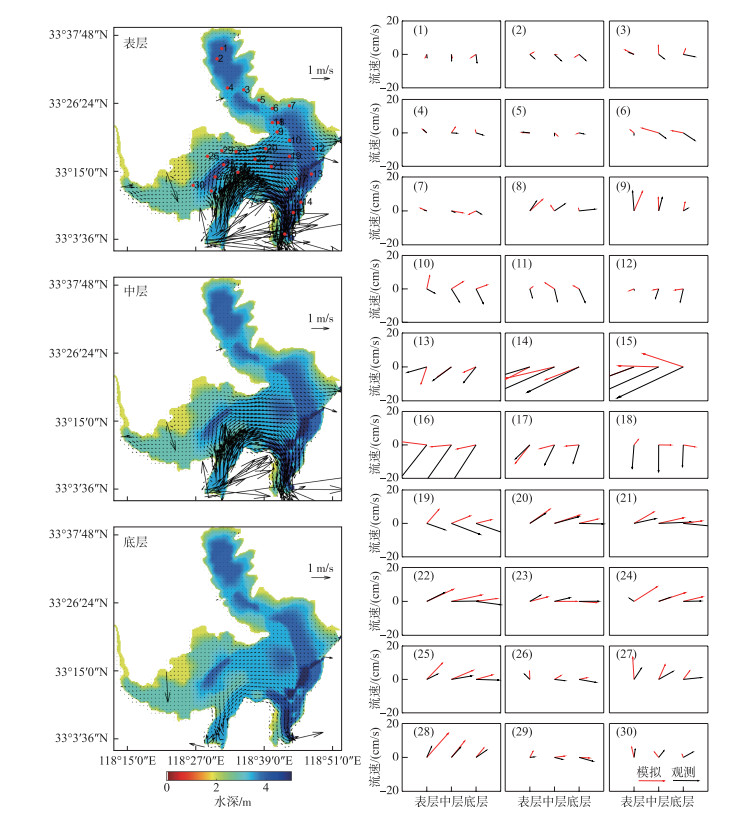
|
图 2 洪泽湖三维水动力2020年8月4日全湖表层、中层与底层湖流的模拟情况(左列)及对于30个点位湖流模拟值与实测值对比(右列) Fig.2 Simulated current pattern at the top, middle and bottom layers on 4 August 2020 (left), and comparison of simulated and observed currents at the 30 monitoring sites in Lake Hongze (right) |
2020年8月4日正值汛期,洪泽湖出入湖流量较大,当日淮河入湖流量达6810 m3/s,环湖河道入湖总流量达到7660 m3/s,三河闸、二河闸、苏北灌溉总渠出湖总流量达到8720 m3/s,洪泽湖的平均水位约为13.64 m. 当日现场监测的湖区风速介于3.33~5.17 m/s之间,风向为东风至东南风. 在较大的出入湖流量和风速驱动下,洪泽湖各层水体流速都较大,在溧河洼观测到的最大流速达到36.2 cm/s. 但湖区间差别较大,成子湖的水体流速远远小于溧河洼. 8月4日洪泽湖30个点位表层、中层和底层水体的平均流速监测值分别为8.45、7.37和5.61 cm/s. 从图 3可以看出,模型可以较好地刻画大部分点位的三维流场特征,但模拟精度空间差异较大,总体对于溧河洼中东部与洪泽湖主体部分模拟精度相对较高,但对于成子湖模拟相对较差. 这主要因为成子湖水体流速远远小于溧河洼水体,且流速流向呈现出较高的空间差异,这给模型准确刻画成子湖湖流时空变化带来了较大挑战,因此总体模拟精度低于其他湖区. 此外,用于验证模型的实测数据为定点剖面观测,而模型计算单元面积为6.25万m2,监测与模型空间尺度的不匹配问题也会给模型的准确评估带来较大困难[11].

|
图 3 洪泽湖水动力模型对于2020年8月4日和11月2日全湖30个点位表层、中层和底层流场模拟的Fn值对比 Fig.3 Comparison of Fn values for currents at top layer, central layer and bottom layer derived from hydrodynamic model for the 30 monitoring sites on August 4th and November 2nd 2020, respectively |
2020年11月2日洪泽湖出入湖总流量分别为218和318 m3/s,风速介于0.44~3.26 m/s之间,洪泽湖的平均水位约为12.77 m. 出入湖流量、风速和水位都远小于8月4日. 当日30个监测点位表层、中层和底层水体的平均流速分别为3.65、2.91和2.92 cm/s. 模型对于30点位表层、中层和底层水体模拟的平均值分别为2.77、2.87和2.65 cm/s,可以看出模型对于洪泽湖水体模拟的流速与实测流速比较接近. 由于篇幅限制,模型对于11月2日流场模拟值与实测值的对比情况未在本文中给出.
模型对于8月4日洪泽湖30个各湖流监测点位表层水体模拟的Fn (归一化傅里叶范数)值介于0.20~5.12之间(图 3),对于位于成子湖中部西岸附近的5号监测点位模拟精度最高,对于溧河洼24号点位监测误差最大. 模型对于中间层水体模拟的Fn值介于0.10~2.69之间;对于底层水体模拟的Fn值介于0.15~1.75之间. 3个水层各点位模拟的Fn平均值分别为1.18、0.94和0.86,说明模型对于底层水体模拟的精度略高于中间层和表层.
模型对于11月2日全湖30个监测点位表层水体模拟的Fn值介于0.10~3.77之间,中层水体模拟的Fn值介于0.16~6.65之间,底层水体的Fn值介于0.08~11.17之间. 模型对于表层、中层和底层各点位模拟的Fn平均值分别为1.36、1.43和1.69. 总体而言,模型对于较大流速的湖流模拟精度较高,对于小流速,且空间变化强烈的湖区流场模拟相对较差.
2.2 不同风向作用下洪泽湖垂向平均湖流特征为全面分析洪泽湖在不同风场驱动下三维风生流特征,模拟了洪泽湖平均水位为12.5 m工况条件下,2.4 m/s(多年平均风速)北风、北偏东风、东北风等16种不同风向条件下洪泽湖垂向平均以及表层、次表层、中间层、次底层和底层各层流场分布特征. 图 4显示了其中北风、东北风、东风、东南风、南风、西南风、西风和西北风8种风向下的全湖垂向平均流场分布情况.
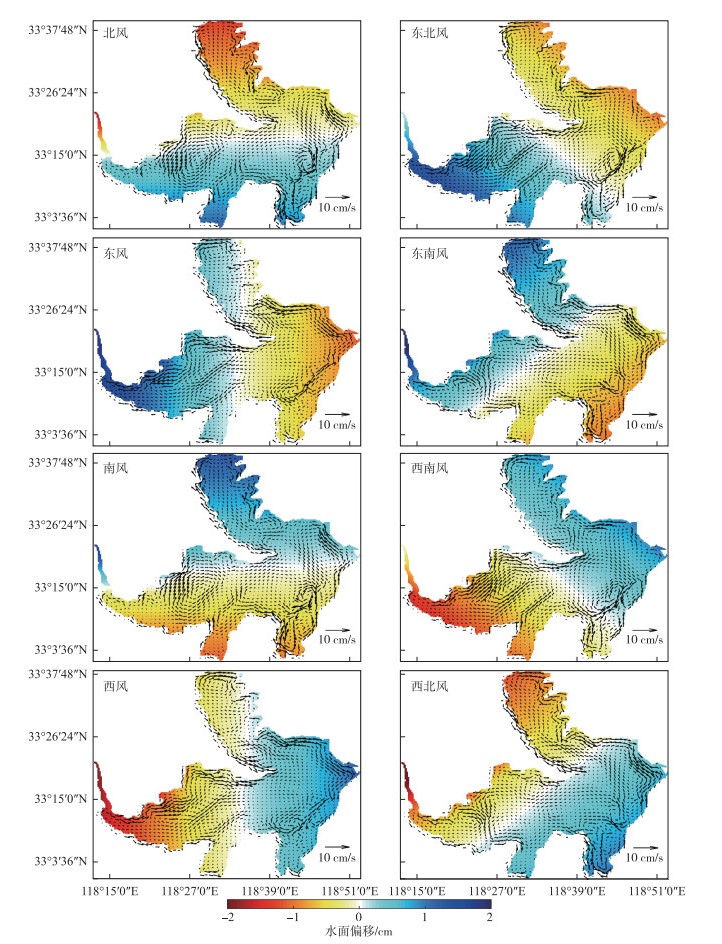
|
图 4 北风、东北风、东风、东南风、南风、西南风、西风和西北风8种风向驱动下洪泽湖垂向平均湖流结构特征 Fig.4 Simulated vertical-averaged current structure of Lake Hongze under 8 wind directions such as northern, northeastern, eastern, southeastern, southern, southwestern, western and northwestern winds |
在不同风向驱动下,洪泽湖垂向平均流场空间结构存在明显的差异. 由于篇幅限制,本文只分析北风和东风作用下流场特征. 北风驱动下,在全湖不同区域形成6~8个大小不一的顺时针或逆时针环流. 在溧河洼中部较大区域形成一个逆时针的环流,同时在环流的西部流速明显大于其他区域. 与此同时,在洪泽湖东岸靠近洪泽附近也存在一个明显的顺时针环流区,该环流区南北两侧流速相对较低,但靠近东北侧的沿岸流流速较快. 在持续的北风作用下,溧河洼和东西两侧沿岸区,以及淮河入湖区以南西部沿岸区流速较快.
在持续的东风作用下,溧河洼中部在北风下产生的逆时针环流消失,但在中南部形成一个不规则的顺时针环流,该环流南北两侧流速较快. 此风场驱动下溧河洼与洪泽湖主体交汇区流速普遍较缓. 淮河入湖区附近也形成了一个规模相对较小的逆时针环流. 与此同时,沿溧河洼北部形成一支流速较快的西向沿岸流,成子湖与洪泽湖主体部分交界湖区两侧也形成了流速较快的西北向沿岸流.
表 1统计了风速为2.4 m/s, 洪泽湖初始平均水位为12.5 m,北风等16种不同风向驱动下洪泽湖4个湖区垂向平均流速分布情况. 分湖区平均流速计算时仅考虑水体的流动速率,即取各湖区包含的所有计算网格的平均水体流速值作为分湖区平均流速,不考虑不同单元流向的差异.
| 表 1 初始水位为12.5 m条件下,2.4 m/s风速,16种不同风向驱动下洪泽湖4个湖区垂向平均流速模拟值 Tab. 1 Vertical-averaged current velocities from model outputs for each of the four basins of Lake Hongze forced by 16 wind directions with wind speed of 2.4 m/s and initial water level of 12.5 m |
2.4 m/s风速驱动下,不同湖区垂向平均流速在0.964~2.216 cm/s之间波动. 可以看出,风向的变化对洪泽湖不同湖区水体垂向平均流速影响较为明显. 溧河洼水体在东北风向下平均流速最大,为1.389 cm/s;在西北风作用下平均流速最小,为1.014 cm/s. 洪泽湖主体部分在南偏东风作用下平均流速最大,为1.405 cm/s;在西偏南风下平均流速最小,为1.232 cm/s. 成子湖水体在东南风作用下平均流速最大,为1.468 cm/s;在南偏西风作用下平均流速最小,为1.078 cm/s. 南部湖区平均流速在北风作用下平均流速最大,为2.216 cm/s;在西风下垂向平均流速最小,为0.964 cm/s. 由此可见,南部湖区水体在不同风向下垂向平均流速差异最大,达到1.252 cm/s,远高于其他湖区. 洪泽湖垂向平均流速主体最小,为0.173 cm/s.
从不同风向下各湖区平均流速来看,南部湖区平均为1.675 cm/s,其次为主体部分,平均为1.320 cm/s. 成子湖与溧河洼分别为1.208和1.282 cm/s. 一般来讲,各湖区长轴(连接湖区内任意两点所能获取的最大长度)的长度越长,且长轴角度与风向的吻合度越高,湖区水体垂向平均流动速率越大. 例如南部湖区湖面总体呈南北走向,因此在南风和北风作用下水体流速最快. 另外,由于洪泽湖形状较为复杂,不同湖区水体流速也受到风驱长度影响,对于同一湖区比如南部湖区,在北风和南风向驱动下的水体流速也存在一定差异.
2.3 东风驱动下洪泽湖垂向分层水体流场结构如图 1b所示,受东亚季风气候影响,洪泽湖大部分东风、东偏南或东偏北风出现频率远远高于其他风向. 1975—2020年长系列风场数据分析结果表明:东风在所有16风向中占比最高,各年平均达到11.5 %;其次是东偏南风,占比达到11.2 %;再次为东偏北风,占比为10.6 %,其他风向占比都在8 % 以下. 西南风和西风出现频率最低,在所有16风向中的占比分别只有3.5 %. 洪泽湖多年平均风速为2.4 m/s. 从分月来看,3月和4月平均风速最高,都为2.7 m/s;其次为5月,平均为2.5 m/s;9月和10月平均风速最低,都为1.9 m/s.
由于东风为洪泽湖出现频率最高的风向,因此本文着重分析东风驱动下洪泽湖垂向分层流场特征. 如图 5所示,在12.5 m初始平均水位,2.4 m/s东风驱动下,洪泽湖流场结构在垂向空间存在明显的差异. 受水下地形、岸线形态等多重要素影响,洪泽湖表层湖流流态也较为复杂,大部分湖区表层流流向与风向整体吻合程度并不高,尤其在半封闭的湖湾处以及沿岸区. 但在开阔的敞水区表层水体流向与风向吻合度较好. 次表层水体流速明显小于表层水体,在持续的东风作用下,溧河洼中部次表层水体形成了一支流速较快的迂回反“S”形水流,同时溧河洼北部水体形成了一支流速较快的西向沿岸流. 中间层水体流向与次表层较为接近,但大部分湖区流速小于次表层水体. 次底层与底层水体流向基本与表层相反,说明洪泽湖垂向空间存在明显的补偿流特征.
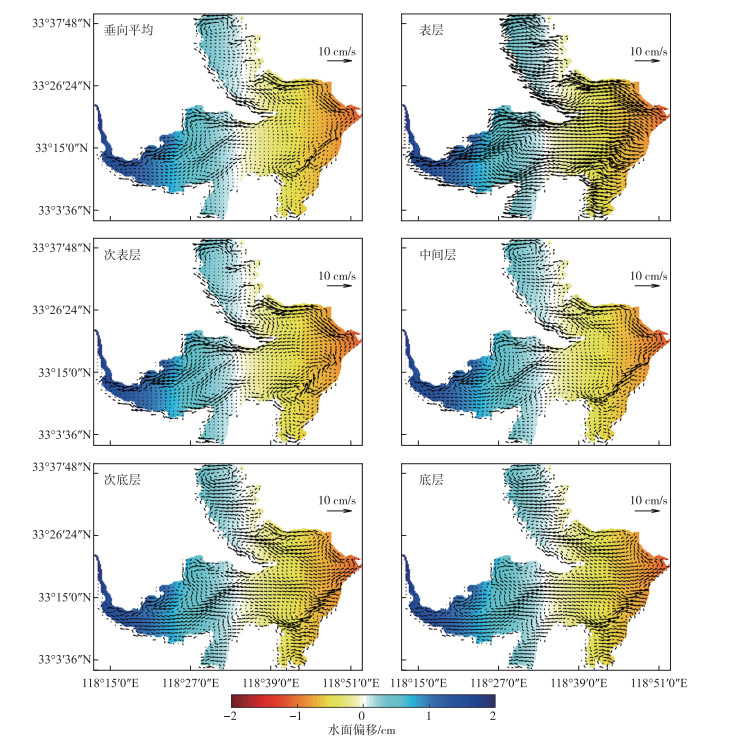
|
图 5 12.5 m水位,2.4 m/s东风驱动下洪泽湖垂向各层流场结构特征 Fig.5 Current structure for vertical layers of Lake Hongze under a 12.5 m water level and 2.4 m/s eastern wind |
除了风向,湖面风速变化也会导致流场发生变化. 湖面风速越大,湖泊表层水体受到风的拖曳力就越大,表层湖水越易向下风方向运动,并引起下风向的涌水和对应上风向的减水,进而增加下风、上风向水面坡度,增加湖水的水平压强梯度力,进而引起湖流流速的增加.
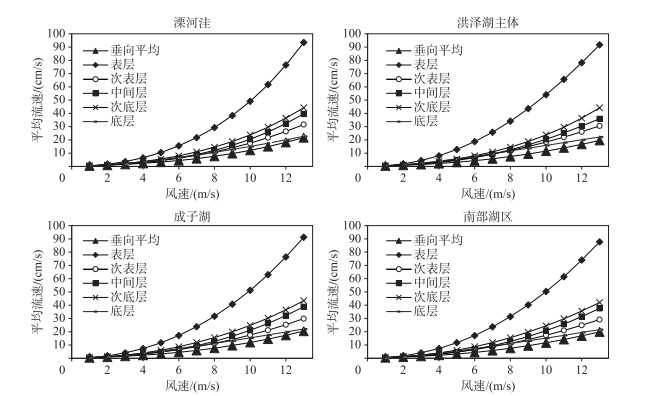
图 6显示了洪泽湖水位为12.5 m时,东风1~13 m/s不同风速条件驱动下洪泽湖4个湖区垂向平均及垂向各层平均流速变化,各湖区各分层水体平均流速计算方法与表 1相同. 洪泽湖各湖区水体流速对风速变化十分敏感,当湖面风速加快时,垂向平均及各层水体流速也快速上升. 但各层水体流速变化与风速加快并不是简单的线性关系,而是随着风速的升高呈加速上升的趋势. 其中表层水体流速上升的幅度远远高于其他水层. 比如溧河洼,当湖面风速为1 m/s时,该湖区表层水体平均流速仅为0.48 cm/s,当湖面风速达到4 m/s时,流速迅速上升到6.55 cm/s,当湖面风速达到13 m/s时,流速上升到76.4 cm/s, 相当于1 m/s风速时的约158倍. 对于垂向各层水体平均流速随风速的上升速度从大到小为表层、次底层、中间层、次表层和底层. 当湖面风速达到13 m/s时,溧河洼水体次底层平均流速为44.27 cm/s,中间层为39.6 cm/s,次表层和底层则分别为31.6和22.7 cm/s.
|
图 6 洪泽湖水位为12.5 m时,1~13 m/s东风驱动下洪泽湖4个湖区垂向平均及垂向各层平均流速变化 Fig.6 Basin-averaged current velocity variations of Lake Hongze for the five vertical layers under 1-13 m/s wind speed of the eastern wind with a water level of 12.5 m |
除了风速风向,水位或水深变化也是影响湖泊流场的重要因素. 图 7显示了2.4 m/s东风驱动下,洪泽湖初始水位从12.1 m抬升至14.0 m时,位于溧河洼的26号点、洪泽湖主体的10号点,成子湖的3号点以及南部湖区的15号点垂向平均流速以及垂向各层平均流速的变化情况,各点位的具体位置如图 1a所示.

|
图 7 2.4 m/s东风驱动下洪泽湖4个点位分层流场随水位变化特征 Fig.7 Changes in vertical current structure at 4 sites in Lake Hongze with different water levels under 2.4 m/s eastern wind |
可以看出,在相同风场作用下,不同点位垂向各层水体流速总体呈现随水位上升而加快的趋势. 但上升的速度随着水位的升高存在一定的空间差异,且部分点位个别水层存在流速和流向都发生较大变化的情况,比如成子湖的3号点位在水位由低升高时,中间层水体流速逐渐升高,且流向由北偏西方向呈顺时针偏转,水位升高至14 m时,流向转为东偏北方向. 该点位次表层水体流场也与其他点位有所差异,表现为随着水位升高而下降的趋势. 另外对于溧河洼的26号点位表层水体,流速随着水位的升高先呈快速升高的趋势,当水位升高至13 m之后,流速升高的趋势有所减缓.
由于各点位中间层、次底层和底层水体流向基本与表层相反,因此各点位垂向平均流速相比各水层明显减小,但各点位减小的速度也存在明显的差异. 如对于1号点位,平均流速由水位12.1 m时的约1.23 cm/s下降至14.0 m水位的约0.76 cm/s,下降幅度达到0.47 cm/s;对于15号点位,平均流速由0.62 cm/s下降至0.41 cm/s, 下降幅度仅为0.21 cm/s.
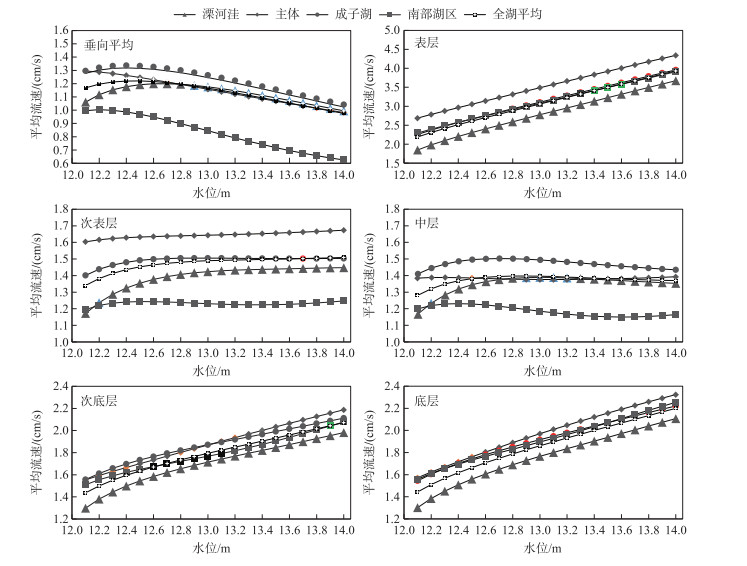
图 8进一步统计了2.4 m/s东风驱动下全湖和4个分湖区在不同水位下的垂向平均和分层平均流速,水体平均流速计算方法与表 1类似,即仅考虑各个计算单元水体流动速率. 结果显示,不同湖区水体流动速率对于水位变化的响应存在明显差异. 对于溧河洼,水位从12.1 m上升时,垂向平均流速从约1.06 cm/s快速上升. 当水位上升至12.7 m时,水体垂向平均流速达到1.20 cm/s的最高值,随后开始下降. 当水位上升至13.7 m时,溧河洼水体平均流速降至约1.05 cm/s,与水位为12.0 m时相当. 当水位升高至14.0 m时,平均流速降至约1.00 cm/s. 对于成子湖和南部湖区,垂向平均流速分别在水位12.4和12.2 m时达到最大,分别为1.32和1.00 cm/s,另外可以看出,南部湖区在东风作用下垂向平均流速远小于其他湖区. 洪泽湖主体部分与其他3个湖区存在一定的差异,水体平均流速随水位上升而表现为一致的下降趋势. 全湖水体垂向平均流速在12.5 m水位下达到最大值,为1.22 cm/s.
|
图 8 2.4 m/s东风驱动下洪泽湖全湖及4个湖区在12.1~14.0 m水位时垂向平均及分层水体平均流速变化 Fig.8 Basin-averaged current velocity variations of Lake Hongze for the five vertical layers under water levels from 12.1 m to 14.0 m at a 2.4 m/s eastern wind |
各湖区表层流速随水位上升都呈现直线上升的趋势,但湖区间表层平均流速值存在一定的差异. 对于次表层,尽管各湖区水体平均流速也表现为随着水位的升高而上升,但在不同水位时上升的速度,即斜率变化有所差异. 总体而言,当水位从12.1 m上升至12.6 m时,各湖区次表层水体流动速度上升较快,随后上升速率趋于平稳. 各湖区中间层水体对于水位变化的响应呈现出较高差异. 溧河洼中间层水体流速对于洪泽湖水位变化响应最为敏感,当水位从12.1 m上升至13.0 m时,溧河洼中间层水体流速快速上升,从1.16 cm/s上升至1.39 cm/s,随后流速缓慢下降. 成子湖与洪泽湖南部湖区中层水体流速变化总体趋势与溧河洼相似,但流速上升的速度远小于溧河洼. 洪泽湖主体部分流速随着水位的升高先呈现轻微上升,随后缓慢下降,至水位13.6 m时降至最低,后复又缓慢上升. 各湖区次底层和底层水体变化趋势非常相似,4个湖区都表现为随着水位上升水体流速升高的趋势.
3 结论在构建与验证洪泽三维水动力模型的基础上,利用长系列数据分析了洪泽湖风场特征. 模拟了16种不同风向驱动下的洪泽湖三维风生流结构特征,并进一步分析了风速和水位变化对分湖区分层流速的影响. 主要结论如下:
1) 水动力模型可以较好地刻画洪泽湖三维湖流变化特征. 模型对于大流速湖流模拟的精度较高,对于小流速且空间差异较大的湖区模拟相对较差. 模型模拟和实测结果都显示,洪泽湖水体流速在垂向上存在明显的差异,表层和底层水体流向总体差异较大,存在明显的补偿流.
2) 洪泽湖风生流结构在不同风向驱动下呈现明显的差异. 北风驱动下,在全湖不同区域形成6~8个大小不一的顺时针或逆时针环流. 东风作用下,溧河洼中部在北风下产生的逆时针环流消失,但在中南部形成一个不规则的顺时针环流,说明湖流结构对于风向变化比较敏感. 在相同风速条件下,溧河洼、洪泽湖主体、成子湖和南部湖区分别在东北风、南偏东风、东南风和北风作用下平均流速最大.
3) 洪泽湖各湖区水体流速对风速变化十分敏感,当湖面风速加快时,垂向平均及各层水体流速也快速上升. 但各层水体流速变化与风速加快并不是简单的线性关系,而是随着风速的升高呈加速上升的趋势. 其中表层水体流速上升的幅度远远高于其他水层. 对于垂向各层水体平均流速随风速的上升速度从大到小为表层、次底层、中间层、次表层和底层.
4) 洪泽湖垂向各层水体流速总体呈现随水位上升而加快的趋势. 但上升的速度随着水位的升高存在一定的空间差异,部分点位个别水层存在流速和流向都发生较大变化的情况. 由于表层和底层水体流向相反,各湖区垂向平均流速变化变化较为复杂. 总体呈现先上升后下降趋势,全湖垂向平均流速在12.5 m水位下达到最大值.
致谢: 王岩、胡月敏、管玉莹等参与了洪泽湖湖流现场观测工作,在此表示感谢.
| [1] |
Mao ZG, Gu XH, Gong ZJ et al. The structure of fish community and changes of fishery resources in Lake Hongze. J Lake Sci, 2019, 31(4): 1109-1119. [毛志刚, 谷孝鸿, 龚志军等. 洪泽湖鱼类群落结构及其资源变化. 湖泊科学, 2019, 31(4): 1109-1119. DOI:10.18307/2019.0401] |
| [2] |
Cai Y, Ke CQ, Shen XY. Variations in water level, area and volume of Hongze Lake, China from 2003 to 2018. Journal of Great Lakes Research, 2020, 46(6): 1511-1520. DOI:10.1016/j.jglr.2020.08.024 |
| [3] |
Liu HD, Zheng ZC, Young B. Three-dimensional numerical simulations of hydrodynamics with algae transport and its biological behaviors in surface water systems. ocean engineering, 2019, 183: 116-131. DOI:10.1016/j.oceaneng.2019.05.007 |
| [4] |
Rao YR, Milne JE, Marvin CH. Hydrodynamics and water quality in western Lake Ontario. Journal of Great Lakes Research, 2012, 38: 91-98. DOI:10.1016/j.jglr.2012.04.001 |
| [5] |
Shen J, Liu ZW, Yang XD et al. Limmology. Beijing: Higher Education Press, 2020. [沈吉, 刘正文, 羊向东等. 湖泊学. 北京: 高等教育出版社, 2020.]
|
| [6] |
Gill AE ed. Atmosphere-ocean dynamics. New York: Academic, 1982.
|
| [7] |
Beletsky D, Schwab D, McCormick M. Modeling the 1998-2003 summer circulation and thermal structure in Lake Michigan. Journal of Geophysical Research: Oceans, 2006, 111(C10): C10010. DOI:10.1029/2005JC003222 |
| [8] |
Yao J, Zhang Q, Li YL et al. The influence of uniform winds on hydrodynamics of Lake Poyang. J Lake Sci, 2016, 28(1): 225-236. [姚静, 张奇, 李云良等. 定常风对鄱阳湖水动力的影响. 湖泊科学, 2016, 28(1): 225-236. DOI:10.18307/2016.0126] |
| [9] |
Hu WP, Qin BQ, Pu PM. Three-dimensional numerical experiments on hydrodynamics in Taihu Lake-3. influence of the reclaimation in Mashan district on wind-driven current. J Lake Sci, 2000, 12(4): 335-342. [胡维平, 秦伯强, 濮培民. 太湖水动力学三维数值试验研究——3.马山围垦对太湖风生流的影响. 湖泊科学, 2000, 12(4): 335-342. DOI:10.18307/2000.0407] |
| [10] |
McCombs MP, Mulligan RP, Boegman L et al. Modeling surface waves and wind-driven circulation in eastern Lake Ontario during winter storms. Journal of Great Lakes Research, 2014, 40: 130-142. DOI:10.1016/j.jglr.2014.02.009 |
| [11] |
Chen YY, Liu QQ. Numerical study of hydrodynamic process in Chaohu Lake. Journal of Hydrodynamics, 2015, 27(5): 720-729. DOI:10.1016/s1001-6058(15)60534-0 |
| [12] |
Liu SE, Ye QH, Wu SQ et al. Horizontal circulation patterns in a large shallow Lake: Taihu Lake, China. Water, 2018, 10(6): 792. DOI:10.3390/w10060792 |
| [13] |
Bennington V, McKinley GA, Kimura N et al. General circulation of Lake Superior: Mean, variability, and trends from 1979 to 2006. Journal of Geophysical Research: Oceans, 2010, 115(C12): C12015. DOI:10.1029/2010jc006261 |
| [14] |
Beletsky D, Hawley N, Rao YR. Modeling summer circulation and thermal structure of Lake Erie. Journal of Geophysical Research: Oceans, 2013, 118(11): 6238-6252. DOI:10.1002/2013JC008854 |
| [15] |
Jiang JH, Huang Q. Numerical simulation of wind-driven current in Hongze Lake. Transaction of Oceanology and Limnology, 1996(3): 7-12. [姜加虎, 黄群. 洪泽湖风生流数值模拟. 海洋湖沼通报, 1996(3): 7-12.] |
| [16] |
Liu YJ, Xu GB. Effects of wind field and throughput flow on the flow field of Hongze Lake. Journal of Water Resources and Water Engineering, 2020, 31(2): 174-178, 184. [刘翊竣, 徐国宾. 风场和吞吐流对洪泽湖流场的影响分析. 水资源与水工程学报, 2020, 31(2): 174-178, 184.] |
| [17] |
Peng ZL, Chen CR, Wan J et al. Water particle tracking in inflow water for Hongze Lake and Lake Chaohu based on Lagrangian method. Oceanologia et Limnologia Sinica, 2020, 51(6): 1275-1287. [彭兆亮, 陈昌仁, 万骏等. 基于拉格朗日方法的洪泽湖与巢湖河流出入湖水体追踪计算. 海洋与湖沼, 2020, 51(6): 1275-1287.] |
| [18] |
Zhang YH, Hu WP, Peng ZL et al. Practical measure research on the spatial characteristics of lake currents in Lake Hongze. Chinese Journal of Hydrodynamics, 2020, 35(4): 541-549. [张怡辉, 胡维平, 彭兆亮等. 洪泽湖湖流空间特征的实测研究. 水动力学研究与进展, 2020, 35(4): 541-549.] |
| [19] |
Karamigolbaghi M, Feng YP, Atkinson JF et al. Circulation and mixing in Sodus Bay due to water exchange with Lake Ontario. Journal of Great Lakes Research, 2019, 45(6): 1090-1102. DOI:10.1016/j.jglr.2019.09.020 |
| [20] |
Hu WP, Pu PM, Qin BQ. A three-dimensional numerical simulation on the dynamics in Taihu Lake, China (Ⅰ): The water level and the current during the 9711 typhoon process. J Lake Sci, 1998, 10(4): 17-25. [胡维平, 濮培民, 秦伯强. 太湖水动力学三维数值试验研究——1.风生流和风涌增减水的三维数值模拟. 湖泊科学, 1998, 10(4): 17-25. DOI:10.18307/1998.0403] |
| [21] |
Hu WP, Pu PM, Qin BQ. A three-dimensional numerical simulation on the dynamics in Taihu Lake, China(Ⅱ): The typical wind-driven current and its divergence. J Lake Sci, 1998, 10(4): 26-34. [胡维平, 濮培民, 秦伯强. 太湖水动力学三维数值试验研究——2.典型风场风生流的数值计算. 湖泊科学, 1998, 10(4): 26-34. DOI:10.18307/1998.0404] |
| [22] |
Hu WP, Qin BQ. A three-dimensional numerical simulation on the dynamics in Taihu Lake, China (Ⅳ): Transportation and diffusion of conservative substance. J Lake Sci, 2002, 14(4): 310-316. [胡维平, 秦伯强. 太湖水动力学三维数值试验研究——4.保守物质输移扩散. 湖泊科学, 2002, 14(4): 310-316. DOI:10.18307/2002.0403] |
| [23] |
Hu WP, Jørgensen SE, Zhang FB. A vertical-compressed three-dimensional ecological model in Lake Taihu, China. Ecological Modelling, 2006, 190(3/4): 367-398. DOI:10.1016/j.ecolmodel.2005.02.024 |
| [24] |
Hu WP, Jørgensen SE, Zhang FB et al. A model on the carbon cycling in Lake Taihu, China. Ecological Modelling, 2011, 222(16): 2973-2991. DOI:10.1016/j.ecolmodel.2011.04.018 |
| [25] |
Huang A, Rao Y, Lu YY et al. Hydrodynamic modeling of Lake Ontario: An intercomparison of three models. J Geophys Res, 2010, 115: C12706. |
 2021, Vol. 33
2021, Vol. 33 

