(2: 长江水利委员会水文局长江中游水文水资源勘测局, 武汉 430012)
(2: Middle Yangtze River Bureau of Hydrology and Water Resources Survey, CWRC, Wuhan 430012, P. R. China)
长江是中华民族的生命河,也是中华民族发展的重要支撑[1]. 长江经济带覆盖面积占全国的21 %,人口和经济总量均超过全国的40 %,是我国经济中心所在、活力所在[2]. 其中,作为长江经济带“一轴、两翼、三极、多点”格局中“三极”之一的长江中游城市群,承东启西、连南接北,以全国3.4 % 的土地面积和9.0 % 的人口数量创造了9.6 % 的经济总量,是长江经济带的重要组成部分,在我国区域发展格局中占有重要地位[3]. 受地理位置与水文条件的综合影响,长江中下游承接长江上游、洞庭湖、汉江、鄱阳湖等洪水,洪水峰高量大、持续时间长[4-6],在极端气候条件下,易遭受洪涝灾害的威胁,为区域经济的良好发展带来了不安因素. 为确保长江流域广大地区人民生命财产安全和经济社会发展,国务院分别于2011和2015年批复了《长江洪水调度方案》和《长江防御洪水方案》,明确长江中下游干流沿岸设有42处蓄滞洪区,总面积约为1.2万km2,包括耕地4745.3 km2,人口约632.5万人,有效蓄洪容积为589.7亿m3. 其中,城陵矶河段(城陵矶-东荆河口)蓄滞洪区调度规定,当三峡水库水位达155.0 m后,如莲花塘站水位达到34.40 m并继续上涨,则需采取城陵矶附近区蓄滞洪区分洪措施. 因此,作为城陵矶河段蓄滞洪区启用指标控制站,莲花塘水位站的水位值极其关键. 然而,受河流形态和江湖关系(长江与洞庭湖)的双重影响,在特殊水情下,莲花塘水位站水位呈现出“潮汐”式不规则周期性波动变化导致水位波动,俗称“假潮”. 已有研究表明,莲花塘水位站“假潮”波动周期一般在0.8~1.0 h之间,最大波动变化幅度可达0.29 m[7]. “假潮”现象给蓄滞洪区启用等工作带来一定决策困扰,如2020年长江干流第2、3次编号洪水期间,莲花塘水位站自7月21日起,在“假潮”作用影响下其水位波动瞬时最大值已达34.40 m并有继续上涨的趋势,根据上述两方案规定,若采纳该“假潮”影响下的瞬时水位值,城陵矶附近区蓄滞洪区需采取分洪措施,然而下一时间段莲花塘水位站水位或将下降并低于指标水位34.40 m,表明不应采取分洪措施,是否启用分蓄洪区对地区国民经济影响重大,受“假潮”影响的水位值是否符合启用蓄滞洪区的判定条件成为了防汛决策部门考量的难题. 因此,通过对城陵矶河段水文特性及水位数据的研究分析,探索“假潮”现象的特点与规律,研究“假潮”水位滤波处理方法具有十分重要的意义.
“假潮”现象早已引起水文水利行业学者的广泛关注,现有研究表明,“假潮”大致划分为两类,原发型“假潮”和传播型“假潮”[8],主要发生在长江中下游、黄河中下游河段,目前以黄河山东段对“假潮”的研究为主. 宋士强等[8]结合黄河下游孙口水文站实际观测资料,对黄河下游地区较小流量级下发生的“假潮”现象进行了系统分析,得出了“假潮”是由于沙波运动在弯道处因控导工程作用产生雍水和回水而引发的一种水位、流速、含沙量在短时间内发生较大幅度变化的水文现象;刘超等[7]对长江中游莲花塘水位站“假潮”现象水位平滑处理方法进行了研究,通过对多种处理方法的综合研究表明,采用3 h加权平滑及综合处理效果较为理想;谷源泽等[9]对黄河山东段“假潮”期水文测报方法进行了分析,认为“假潮”期水文测验用前一日平均水位代表法较为方便实用,而过程测验法尽管报汛精度较高,但由于受各种条件限制,目前还难以实现;李春莲等[10]对黄河下游河段水文资料整编中“假潮”现象的数据分析与处理进行了研究,提出了利用水量平衡原理进行平差计算,较好地解决了“假潮”引起的系统误差问题. 与黄河中下游山东段“假潮”现象时机、成因不同,长江中游城陵矶河段“假潮”主要在主汛期发生,在越接近洪峰时水位波动越大,刘超等[7]认为该河段主要受弯道干扰波影响,是一种出现在河道两岸交相传播的一种能量波,但尚未对该河段“假潮”规律进行研究. 本文结合莲花塘水位站地理位置和已有研究成果,选取监利水文站、城陵矶(七里山)水文站、螺山水文站和莲花塘水位站近5年18个月的水文数据进行研究分析,研究“假潮”发生判别标准与“假潮”现象出现规律,计算“假潮”发生模型,并分析“假潮”水位数据滤波处理方法,以期降低“假潮”现象对莲花塘水位站水位报汛数据的影响,为蓄滞洪区启用等工作的合理决策提供有力的数据支撑.
1 研究区域概况长江是我国第一大河,全长6300余千米,坐西向东流经11个省(区、市),支流涉及8个省(区),流域面积180万km2,长江防洪安全关系流域广大地区人民生命财产安全和经济社会发展. 长江中游河段自宜昌至江西鄱阳湖口,长955 km,集水面积约68万km2. 洞庭湖(28°44′~29°35′N,111°53′~113°05′E)是我国第二大淡水湖,也是长江中游重要的过水吞吐湖泊[11],长江来水自松滋口、藕池口、太平口入湖,自城陵矶出湖,誉为“长江之肾”,兼具河流与湖泊双重属性[12],作为长江流域重要的调蓄湖泊,洞庭湖具有强大的蓄洪能力[13]. 城陵矶(七里山)水文站是洞庭湖出口汇入长江的重要控制站[14],被誉为洞庭湖及长江流域水情“晴雨表”,多年平均年径流量达2600亿m3,占长江中游干流螺山水文站多年平均年径流量的41.10 %. 江湖交汇口建有莲花塘水位站,为长江干流主要控制站,也是长江中游城陵矶河段蓄滞洪区启用的指标控制站,该站水位在防汛调度与决策上占有十分重要的作用.
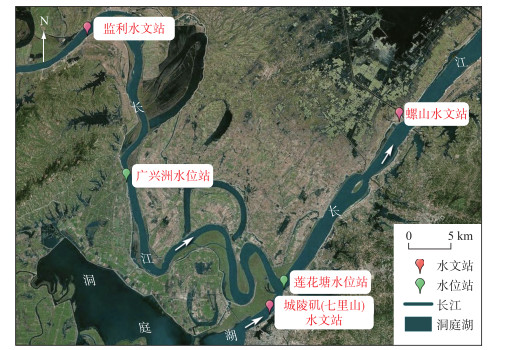
2 材料与方法 2.1 数据来源根据洞庭湖出湖口河流分布特征,本研究以莲花塘水位站为中心,选取其长江干流上游监利水文站、下游螺山水文站和洞庭湖出口城陵矶(七里山)水文站作为研究对象,测站分布见图 1. 根据莲花塘水位站水位等级,选取2016年6-8月、2017年7-10月、2018年5-8月、2019年6-8月、2020年6-9月连续5年高水期水位作为研究对象,数据来源于长江水利委员会水文局长江中游水文水资源勘测局水位自记数据及整编数据(水位数据采用冻结基面高程,水位自记仪满足精度要求).
|
图 1 洞庭湖出口河段测站布置 Fig.1 Hydrometric station layout of Lake Dongting outlet reach |
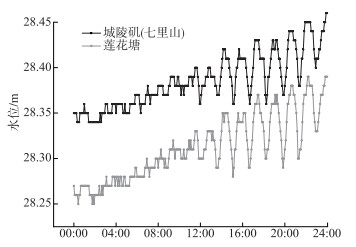
通过对莲花塘水位站2016-2020年中18个月的5 min水位自记仪数据进行分析,根据水位数据“小涨落多、大涨落少”和渐变特征(图 2),提取每日24 h内连续水位变幅的第10个百分位数(记为D10%)作为当日水位波动值(记为D). 通过对2020年莲花塘水位站1-5月5 min水位自记数据的研究发现,当日水位平均波动均值为0.03 m,其中92.76 % 的水位波动值≤ 0.05 m,我们认为该波动主要受莲花塘水位站周边来往船舶及风浪对水位数据的影响. 根据《水位观测标准》(GB/T 50138-2010),自记水位计的比测结果要求置信水平95 % 的综合不确定度不应超过3 cm,校测水位与自记水位系统偏差不应超出±2 cm范围,因此,本文约定单日水位波动值D>0.05 m时,视为发生“假潮”现象.
|
图 2 2020年6月19日城陵矶(七里山)水文站和莲花塘水位站24 h 5 min水位波动 Fig.2 Water level fluctuation of Chenglingji (Qilishan) hydrology station and Lianhuatang water level station in 24 h and 5 min on June 19, 2020 |
为研究与“假潮”现象产生的关联因子,本文选取洞庭湖出口控制站城陵矶(七里山)水文站、长江干流上游监利水文站、下游螺山水文站的日平均流量、水位数据,以及莲花塘日平均水位数据,提取流量占比Q %、相邻站水位落差ΔZ、和各站流量Q、水位Z、单日涨落率J作为潜在自变量,计算监利占螺山流量比(Qjl %)、城陵矶(七里山)占螺山流量比(Qcl %)、监利至莲花塘水位落差(ΔZjl)、城陵矶(七里山)至莲花塘水位落差(ΔZcl)、莲花塘至螺山水位落差(ΔZlls),以及各站流量(Qx)、水位(Zx)、单日涨落率(Jx)(x为站名首字母,螺山站用ls表示). 经Pearson相关分析后,去除非显著相关和相关性弱的参数,再进行二元Logistic回归分析.
2.2 研究方法 2.2.1 二元Logistic回归分析法二元Logistic回归分析法是一种用于检验因果关系假设和两分类预测的分析方法,适用于因变量Y为定性数据,并且只有两种状态. 一般要求样本数量大于自变量X数量的15倍以上,因变量Y中发生数量占样本总数的15 % 以上. 本文主要采用该方法研究“假潮”发生的影响因子,并提出判定模型. 其分析模型为:
| p=11+e−(α+β⋅x) | (1) |
变形后:
| ln(p1−p)=α+β⋅x | (2) |
一般表示为:
| ln(p1−p)=α+β1⋅x1+β2⋅x2+⋯+βn⋅xn | (3) |
式中,p表示Y=1的概率;α表示为回归方程的截距;βi为回归系数,表示某一因素xi改变一个单位时,事件发生与不发生的概率之比的对数变化值.
2.2.2 快速傅立叶变换法快速傅立叶变换(FFT)作为离散傅里叶变换(DFT)的快速算法,一直以来都是频谱分析的重要工具[15],1965年由美国科学家J.W.库利和T.W.图基提出. 本文依据FFT的滤波原理对水位波动数据进行滤波处理,通过快速傅立叶变换将时间域信号转化为频率域信号,再将频率域中的某些频率成分的振幅置零,最后运用快速傅立叶逆变化转化为时间域实现滤波. 其主要计算公式为:
| y(n)≈M∑i=0xn−1(i)e−j2πNki | (4) |
式中,y(n)为滤波输出值;xn为时域离散信号值;M为时域离散信号值xn之前的信号点数;N=M+1;k=0, 1, …, M.
2.2.3 局部加权回归算法局部加权回归算法(local regression)[16]由Cleveland于1979年提出,是对两维散点图进行平滑的常用方法,它结合了传统线性回归的简洁性和非线性回归的灵活性. 当要估计某个响应变量值时,先从其预测变量附近取一个数据子集,然后对该子集进行线性回归或二次回归,回归时采用加权最小二乘法,即越靠近估计点的值其权重越大,最后利用得到的局部回归模型来估计响应变量的值,用这种方法进行逐点运算得到整条拟合曲线.
本文通过R语言中loess函数完成水位数据滤波计算,其中权重wi采用tri-cubed weight function确定,公式如下:
| wi={1−(didmax)3}3当di<dmax时0当di≥dmax时 | (5) |
式中,di为观测点xi到拟合点x*的距离,即di=|xi-x*|;dmax为最大距离,即权重函数趋近于零的距离,或称为半窗口宽度;dmax确定时,常与R语言中的滑动参数span有关.
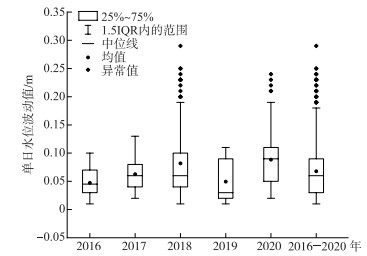
3 结果与讨论 3.1 水位波动值与水文数据特征从莲花塘水位站2016-2020年高水期5 min水位自记数据来看,水位波动瞬时值在0.01~0.37 m范围内浮动,最大波动瞬时值发生在2018年7月7日;经数据处理后,单日水位波动值范围在0.01~0.29 m之间,最大值发生在2018年7月6日. 单日水位波动值D样本数552个,其中D>0.05 m样本数为282个,占样本总数的51.09 %,2016-2020年水位波动数据箱线图见图 3. 由图 3可知,分析月份中,从近5年单日水位波动变化幅度来看,年际间水位波动范围差异明显,表现为D2018>D2020>D2017>D2019>D2016,其中2018年最大值为2016年最大值的2.9倍;从单日水位波动均值来看,年际间水位波动较为集中,在0.05~0.09 m范围内变化,2020年波动均值最大,2016年、2019年波动均值最小,近5年单日水位波动值D均值为0.07 m,中位数为0.06 m,第25 % ~75 % 个数据集中在0.03~0.09 m之间.
|
图 3 莲花塘站2016-2020年单日水位波动值箱线图 Fig.3 Box plot of single-day water level fluctuation of Lianhuatang station from 2016 to 2020 |
研究对象自变量特征值(表 1)可知监利站、城陵矶(七里山)站、螺山站日均流量分别在9180~39300、1150~49200、16800~59300 m3/s之间;监利占螺山流量比Qjl % 在15.83 % ~97.75 % 之间,变化幅度达81.92 %;各站日均水位差值均在9.59~10.75 m之间,水位变化幅度基本一致;监利至莲花塘水位落差最小值为0.61 m,发生在2017年7月5日,监利站日均水位为34.66 m,莲花塘站日均水位为34.05 m,当日莲花塘至螺山水位落差为0.86 m,接近落差最小值(0.84 m),说明长江干流出流不畅,顶托现象严重. 监利、城陵矶(七里山)、莲花塘三站单日水位涨落率特征值基本一致.
| 表 1 自变量特征值 Tab. 1 Characteristic values of independent variables |
对研究对象运用SPSS 20.0软件进行单因素筛查分析,采用Pearson相关系数法对各变量进行相关性分析,显著性检验为双侧检验,选取水位波动值与各变量相关性分析结果见表 2.
| 表 2 Pearson相关性检验结果 Tab. 2 Pearson correlation test results |
由表 2可知,自变量与水位波动值均呈现显著相关,除ΔZlls外,其余自变量均在P < 0.01水平上显著相关,其中监利日均流量相关系数最大,为0.816,其余项相关系数均小于0.7,整体而言相关性较弱,解释能力不强. 造成该结果的可能原因其一是影响水位波动现象的关键因素不在本次分析之列,其二是由于样本数量较多,水位变化幅度大使得数据典型性不强. 仅从各站间相关系数分析而言,可以看到监利站的流量、水位、落差数据相关性明显强于城陵矶(七里山)站、莲花塘站和螺山站. 对此,结合本文研究目的,选取满足监利站高水位(Zj≥34.00 m)的167个样本数据进行Pearson相关性分析. 结果表明,除Qls、Jj外,其余自变量均在P < 0.01水平上与水位波动值显著相关,相关系数较整体样本显著提升,其中强相关性的指标有监利日均流量Qj、监利占螺山流量比Qjl %、城陵矶(七里山)占螺山流量比Qcl %、监利至莲花塘水位落差ΔZjl.
根据发生“假潮”判别标准,将水位波动值D进行二元分类,即D>0.05 m表示为1,反之表示为0. 在167个样本数据中,分类为1的样本数114个,占比68.26 %. 根据单因素筛查分析结果,选取监利日均流量Qj、监利占螺山流量比Qjl %、监利至莲花塘水位落差ΔZjl和监利日均水位Zj与二元分类变量运用SPSS 20.0软件进行二元Logistic回归模型分析,分析方法为Enter. Hosmer和Lemeshow检验结果(P=0.955)表明模型和真实数据拟合良好(表 3).
| 表 3 二元Logistic回归变量结果 Tab. 3 Binary Logistic regression variable results |
结果表明,监利日均流量Qj、监利占螺山流量比Qjl %、监利至莲花塘水位落差ΔZjl和监利日均水位Zj 4个变量中,仅ΔZjl显著(P < 0.05),表明仅ΔZjl是发生“假潮”的独立影响因素. 通过对监利站高水位(Zj≥34.00 m)的167样本数据进行统计,结果如图 4,研究发现当ΔZjl>2.50 m时,发生“假潮”样本数为114个,发生比例为95.00 %,当ΔZjl>2.75 m时,“假潮”发生比例为100 %. 反之表明本次统计样本中,发生“假潮”时均满足ΔZjl>2.50 m.

|
图 4 监利站高水位期间”假潮”发生比例与落差ΔZjl的关系 Fig.4 The relationship between the occurrence ratio of "false tide" and ΔZjl drift at Jianli station during high water level |
对是否发生“假潮”进行预测模型分析,方法采用Forward:conditional,分割点取0.5,Hosmer和Lemeshow检验结果(p=0.672)表明模型和真实数据拟合良好. 其中单个变量ΔZjl的模型分析结果,α=-69.98,β1=27.16,方程表达式为:
| P=11+e69.98−27.16ΔZjl(当Zj≥34.00时) | (6) |
式中,P为“假潮”发生概率;e为自然常数;ΔZjl为监利至莲花塘水位落差.
根据预测模型结果,由公式(6)可知,ΔZjl为影响“假潮”发生概率的主要影响因子. 通过对公式(6)进行验证分析(计算结果P>0.5时,预测值=1,反之为0),结果表明,当观测结果为0时(即D≤0.05 m,未发生“假潮”),该模型预测结果为0的百分比校正值为92.5 % (49/53),当观测结果为1时(即D>0.05 m,发生“假潮”),该模型预测结果为1的百分比校正值为98.2 % (112/114),综合百分比校正值为96.4 % (161/167),表明模型建立效果理想,ΔZjl为发生“假潮”的主要影响因子.
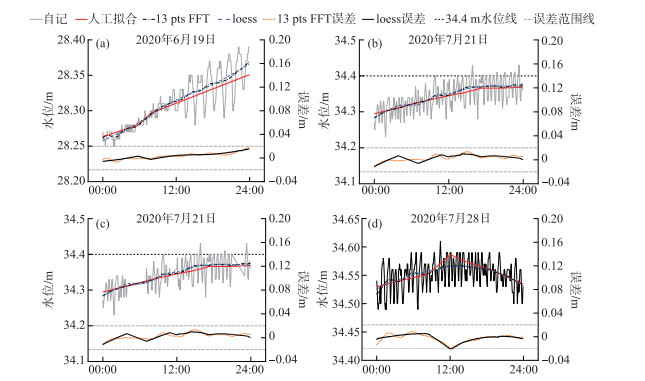
3.3 FFT、local regression滤波结果根据单日水位波动值特征,本文分别运用OriginPro 2016与R语言对莲花塘水位站2020年6月19日(2020年首日出现“假潮”)、7月21日(2020年首日5 min水位瞬时数据破保证水位)、21日(模拟4~6 h、11 h、22~22 h数据丢失)、28日(2020年最高水位出现日)单日5 min自记水位数据采用FFT、local regression方法进行滤波处理. 根据滤波后的线型变化趋势,以及与人工拟合结果的一致性,研究确定FFT分析中pts取值13,local regression分析中span取值0.75. 两种方法滤波结果如图 5所示,滤波后采用值与人工拟合值进行误差计算(视人工拟合数据为真值),误差结果箱线图如图 6所示.
|
图 5 莲花塘水位站2020年特征日变化水位滤波结果 Fig.5 Filtering results of characteristic diurnal variation water level of Lianhuatang water level station in 2020 |
|
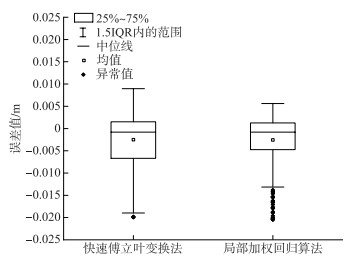
图 6 快速傅里叶变换法与局部加权回归算法误差值箱线图 Fig.6 Box plot of error values of fast Fourier transform and local regression algorithm |
通过对滤波后曲线与人工拟合曲线比较分析,结果表明,FFT、local regression滤波结果与人工拟合曲线水位差均绝对值小于0.02 m,滤波结果可靠. 从图 5a可以看到,当瞬时波动值≤0.05或>0.5时,采用FFT、local regression滤波方法对波动数据进行平滑处理的方法均适用,说明该两种方法适用于不同振幅的波形态数据分析. 从图 5b可以看到,当莲花塘水位瞬时数据超过保证水位34.40时,滤波后数据不受瞬时数据影响.
另一方面,与时间加权平均法需参照最近2点的趋势延长来获取合理的水位不同[7],从图 5中24 h数据可以看出,FFT、local regression滤波法计算结果均不受水位瞬时值的影响,可以准确地计算出相应水位. 从图 5b、c比较可知,当设备数据采集端或接收端故障导致数据空缺时(如空缺1、2、3 h数据),拟合计算结果不受数据丢失影响.
从快速傅里叶变换法与局部加权回归算法误差值箱线图来看,两种方法误差均值均为-0.003 m,中位数值均为-0.001 m,表明滤波结果整体误差较小;快速傅里叶变换法上、下四分位数值(25 % ~75 %)集中在-0.007~0.002 m之间,局部加权回归算法上、下四分位数据(25 % ~75 %)集中在-0.005~0.001 m之间,表明局部加权回归算法误差值波动情况小,数据更集中. 两种滤波方法的误差绝对值均在0.02 m之间,表明两种方法均满足生产要求,具有一定的实际用途,但从误差值的波动情况来看,局部加权回归算法更适用于对波动水位数据的处理.
3.4 水位波动成因分析与对策展望城陵矶河段发生“假潮”现象是弯曲河道水力学特点所决定的. 从图 1可以看到,长江中游监利至莲花塘河段河道极为弯曲,河流弯曲系数Ka为1.74,广兴洲至莲花塘河段Ka达1.91. 同时,在长江干堤的保护下,城陵矶河段水面宽度变化不大,当水流过弯时,流速降低,水面抬高,导致弯前河段水面比降减小,上游来水会短时间在弯道内蓄积,当水位抬升到一定高度后,弯后河段水面比降增大,出口流速增大,流量增加,弯道内槽蓄水量进入下一个弯道,此过程在每一个弯道内循环,调蓄河道来水. 最终,莲花塘水位站上游河段来水在多个弯道串联调蓄作用下进入三江口(莲花塘水位站所在位置)弯道,在洞庭湖出口水流叠加影响下,两股水流能量相互抵消,弯道内流速降低、水位抬高作用更加显著,进一步放大了水位波动,形成“假潮”,与黄河中下游孙口至泺口河段形成“假潮”原因相似[6]. 城陵矶(七里山)水文站对岸七弓岭河段自1998年修建防洪大堤后,长江来水不能直接从七弓岭抵达三江口,而需“掉头”北上后,再南下抵达莲花塘站,进一步加剧了“假潮”现象的水位波动值.
目前对于有过多“噪声”的数据,根据数据本身的完整性、波动幅度和时间连续性等一般采用滑动平均法(mean average)、指数滑动平均法(exponential mean average)、SG滤波法(Savitzky Golay Filter)、时间加权平均法(time weighted average)和平滑处理(smooth)等方法,刘超等[7]根据时间加权平均法采用最接近报汛时段的前1.5 h的2 h加权平滑值,并参照最接近2点的趋势延长得到了较为合理的报汛水位,基本解决了数据波动问题,但该方法中根据最接近2点做趋势延长的做法实质是一种“预测”. 本研究中,莲花塘水位站的报汛数据直接来源于水位自记设备采集的5 min瞬时数据,从图 5可以看到,当水位呈现波动变化时,报汛数据则具有一定的不确定性. 本文采用通讯工程中常使用的FFT滤波平滑处理方法和局部加权回归法对不规则波动水位数据进行处理,分析结果表明,滤波后平滑曲线走势与人工拟合曲线基本吻合,水位差值均小于0.02 m,表明平滑处理后的数据可靠,报汛水位与人工拟合“走中线”最大误差可达0.14 m,而基于该两种算法处理后的水位可以将该误差降低至0.02 m以下. 同时,该方法适用于不同振幅的波形态数据分析,在汛期和非汛期均有效果,但中低枯水位级下,水位滤波必要性不足. 此外,滤波后数据不受短时间数据丢失影响,不受瞬时数据影响,是实测数据的分析结果,本研究中选取的是3段24 h数据独立分析,数据时间跨度长,数据量丰富,计算结果可信度高. 若将该算法应用到现有水情报汛系统中,在数据采集端或分中心接收端预置,则可以有效降低水位报汛误差,为防汛主管部门提供科学合理的实时水位数据,避免波动数据给防汛决策带来的干扰.
本次研究中,仅对历年中部分数据进行了系统性分析,难免会因样本量不足而出现分析误差,另一方面,对于两种滤波方法的适用性分析中,分析所选取的3个代表天水位数据基本完整,虽然对1~3 h内数据丢失的情况进行分析,但没有对存在明显异常数据(如一天中出现大量0值)的24 h数据进行分析,这些都需要在在后续的工作中进一步论证、分析和完善. 若通过对更长时间数据丢失进行计算发现滤波处理结果仍然可靠的话,对于类似于因仪器故障导致的0值的异常值,可以在数据处理之前进行预处理,舍弃异常数据后再进行分析.
4 结论因受河流形态和江湖关系(长江与洞庭湖)的双重影响,作为长江中游城陵矶河段蓄滞洪区启用指标控制站的莲花塘水位站,其水位呈现出的“假潮”变化给蓄滞洪区启用等工作带来了一定决策困扰. 为此,本文通过对莲花塘水位站近5年18个月份的5 min水位自记数据进行分析,确定了发生“假潮”现象的判别标准,再通过二元Logistic回归分析揭示影响“假潮”的主要因子,最后通过对比快速傅里叶变换法与局部加权回归两种算法,提出了应对“假潮”发生后水位序列处理的有效方法. 具体主要结论如下:
1) 单日水位波动值D>0.05 m为发生“假潮”现象的判别标准;近5年单日水位波动值D均值为0.07 m,中位数为0.06 m,第25 % ~75 % 个数集中在0.03~0.09 m之间.
2) 二元Logistic回归分析结果表明,监利站高水位(Zj≥34.00 m)期间, 当ΔZjl>2.50 m时,“假潮”发生比例为95.00 %,当ΔZjl>2.75 m时,“假潮”发生比例为100 %. 模型预测结果综合百分比校正值为96.4 %,表明模型建立效果理想,ΔZjl为发生“假潮”的主要影响因子.
3) 快速傅里叶变换法和局部加权回归算法滤波平滑处理结果表明,24 h 5 min数据采用两种滤波方法进行滤波处理结果可靠;选择方法适用于不同振幅的波形态数据分析,不受短时间数据丢失影响,不受水位瞬时值的影响,具有较大的实用价值. 从误差值的波动情况来看,局部加权回归算法误差值波动更小,更适用于对波动水位数据的处理.
| [1] |
Zhang WW, Ma Q, Li MZ et al. Hatch dates and growth rates of grass carp(Ctenopharyngodon idellus) and silver carp(Hypophthalmichthys molitrix) juveniles in Three Gorges Reservoir, Lake Dongting and Lake Poyang. J Lake Sci, 2020, 32(3): 804-812. [张文武, 马琴, 黎明政等. 三峡水库和长江中下游通江湖泊(洞庭湖和鄱阳湖)草鱼、鲢的孵化日期及早期生长特征. 湖泊科学, 2020, 32(3): 804-812. DOI:10.18307/2020.0320] |
| [2] |
XI J. A speech at the forum on further promoting the development of Yangtze River Economic Zone(4/26/2018). Party Construction Articles: first half of the month, 2018(7): 4-9. |
| [3] |
State Council. The State Council's reply to the development plan for urban agglomerations in the middle reaches of the Yangtze River. Gazette of the State Council of the People's Republic of China, 2015(11): 22-23. [国务院. 国务院关于长江中游城市群发展规划的批复. 中华人民共和国国务院公报, 2015(11): 22-23.] |
| [4] |
Xiao X, Mao BP, Wu SQ. Dynamics of hydrological characteristics in Changjiang River and Lake Dongting confluence reach in the past 100 years. J Lake Sci, 2020, 33(1): 266-276. [肖潇, 毛北平, 吴时强. 近100年来长江与洞庭湖汇流河段水文特征演变. 湖泊科学, 2020, 33(1): 266-276. DOI:10.18307/2021.0119] |
| [5] |
Gao Y, Xie YH, Zou DS et al. Changes and driving factors of water surface area for inner lakes in Lake Dongting district in the past 40 years. J Lake Sci, 2019, 31(3): 755-765. [高耶, 谢永宏, 邹冬生等. 近40年洞庭湖区内湖水面面积变化及其驱动因素. 湖泊科学, 2019, 31(3): 755-765. DOI:10.18307/2019.0314] |
| [6] |
Fang CM, Zhong ZQ. The influence of capacity decrease on flood stages in Dongting Lake and in Yangtze River. Journal of Hydraulic Engineering, 2001, 32(11): 70-74. [方春明, 钟正琴. 洞庭湖容积减小对洞庭湖和长江洪水位的影响. 水利学报, 2001, 32(11): 70-74. DOI:10.3321/j.issn:0559-9350.2001.11.012] |
| [7] |
Liu C, Peng YH, Peng YM et al. Research on smooth treatment of false tide of water level. Journal of Changjiang Engineering Vocational College, 2011, 28(1): 27-28, 34. [刘超, 彭艳华, 彭艳明等. 水位"假潮"现象平滑处理方法研究. 长江工程职业技术学院学报, 2011, 28(1): 27-28, 34. DOI:10.3969/j.issn.1673-0496.2011.01.011] |
| [8] |
Song SQ, Li FJ. Analysis on the cause of ″false tide″ in the lower reaches of the Yellow River?. Zhihuang Keji Xinxi, 2017, 246(2): 3-5. [宋士强, 李福军. 黄河下游河段″假潮″成因分析. 治黄科技信息, 2017, 246(2): 3-5.] |
| [9] |
Gu YZ, Liu YQ, Cui CJ et al. Analysis of hydrological prediction methods in the "false tide periods" in Shandong reaches of the Yellow River. Yellow River, 2001, 23(3): 22-23. [谷源泽, 刘以泉, 崔传杰等. 黄河山东段"假潮"期水文测报方法分析. 人民黄河, 2001, 23(3): 22-23. DOI:10.3969/j.issn.1000-1379.2001.03.012] |
| [10] |
Li CL, Fu CL, Zhang JM et al. Analysis and treatment on "false tide" in hydrologic data reorganization. Journal of Water Resources and Water Engineering, 2009, 20(2): 153-155. [李春莲, 付春兰, 张建民等. 水文资料整编中对"假潮"现象的分析与处理. 水资源与水工程学报, 2009, 20(2): 153-155.] |
| [11] |
Fu X, Zhao QX, Sun ZH. Effects of 175 m experimental operation of the Three Gorges Reservoir on the storage capacity of Lake Dongting. J Lake Sci, 2019, 31(6): 1713-1725. [付湘, 赵秋湘, 孙昭华. 三峡水库175m试验性蓄水期调度运行对洞庭湖蓄水量变化的影响. 湖泊科学, 2019, 31(6): 1713-1725. DOI:10.18307/2019.0603] |
| [12] |
Tang C, Qian B, Li WQ et al. Pollution characteristics and risk evaluation of heavy metals in surface sediments of Dongting Lake. Yangtze River, 2020, 51(6): 49-56, 62. [唐聪, 钱宝, 李炜钦等. 洞庭湖区表层沉积物重金属污染特征与风险评价. 人民长江, 2020, 51(6): 49-56, 62.] |
| [13] |
Qian B, Tang C, Yang Y et al. Pollution characteristics and risk assessment of heavy metals in the surface sediments of Dongting Lake water system during normal water period. European Journal of Remote Sensing, 2021, 54(sup2): 211-221. DOI:10.1080/22797254.2020.1763207 |
| [14] |
Ke WL, Chen CZ, Ji HX et al. A loop-like relationship between water surface area of Lake Dongting and water level at Chenglingji, the Yangtze River. J Lake Sci, 2017, 29(3): 753-764. [柯文莉, 陈成忠, 吉红霞等. 洞庭湖水面面积与城陵矶水位之间的绳套关系. 湖泊科学, 2017, 29(3): 753-764. DOI:10.18307/2017.0325] |
| [15] |
Yang J, Lv JQ. Study on FFT filtering error. Communications Technology, 2010, 43(6): 235-237, 240. [杨君, 吕镜清. FFT滤波误差分析. 通信技术, 2010, 43(6): 235-237, 240.] |
| [16] |
Cleveland WS. Robust locally weighted regression and smoothing scatterplots. Journal of the American Statistical Association, 1979, 74(368): 829-836. DOI:10.1080/01621459.1979.10481038 |
 2022, Vol. 34
2022, Vol. 34 


