除了时段内流量均值或极值之外[1],河流的径流特征也常以频率分布来表征,并被广泛用于造床流量计算、输沙效率分析、防洪工程设计等方面[2-3]. 在大河流域中下游的冲积性河段,流量过程一方面受到河漫滩、湖泊洼地的调节,另一方面又不断塑造沿程洪枯各级河槽,这种双向耦合效应使得流量的频率分布展现出较为复杂的特点[3]. 当前,气候变化和大型水利工程已引起了长江中下游流量过程发生明显变化,从频率分布的角度开展量化分析,并评估这些变化对河床调整可能产生的作用,是亟需开展的工作.
流量频率分布的描述常通过经验频率统计与理论曲线拟合两个步骤[1]. 在工程水文领域,以年最大洪峰、洪量等为对象的频率分析已较为成熟[4]. 尽管流域产汇流特性不同,但大部分水文站的极值频率分布近似符合某种函数. 如我国规范中推荐的皮尔逊Ш型(P3)分布曲线在实践中就取得了较好效果,为水利工程规划设计和水资源配置提供了大量支撑[1, 4-6]. 但当应用于河流地貌领域,统计对象是长时段内全体日均流量的连续序列时,基于年极值这类独立变量的经验往往不再适用[7].
连续流量序列具有两方面特殊性. 首先,序列中的变量并不一定满足独立性,例如同一场降雨导致的洪水事件延续数日甚至数十日,期间的流量具有明显相关性. 其次,不同河流以及同一河流年内不同时期的流量可能由融雪、季风等不同过程导致,并且枯期基流、汛期漫滩洪水受到下垫面渗流、河道槽蓄等不同作用影响,水流产、汇和传播的主导因素具有明显时间和空间差异性. 由于这些特点,P3型分布不再适用,甚至难以找到普适的理论频率分布曲线实施拟合[7-8]. 如Nash对美国55条河流的统计发现,流量频率分布展现出单峰、双峰、多峰等多种类型,其中的单峰型可大致以对数正态(LN)分布描述,而其他类型不符合任何一种常见概率密度函数[7];Ma等对无定河流域4个不同地貌区支流的流量统计显示,尽管频率分布为单峰型,但却均不符合欧美学者建议的LN分布[8]. 此外,也有少数研究注意到,连续流量序列的频率分布之所以呈现复杂特点,在于主导因素的季节差异性,若对汛枯流量分开实施频率分布拟合,则可简化该问题. 如Fennessey和Vogel针对美国23条河流,将累积频率大于50 % 的枯水流量频率采用LN分布进行拟合[9];Segura和Pitlick针对美国融雪河流上32个测站,将累积频率小于50 % 的中洪水流量频率采用分段幂函数(BPL)分布进行拟合[10]. 这些尝试均取得了较好效果,但这些方法是否可用于更多流域,分段的流量频率曲线蕴含了主导因素的哪些物理特性,仍需更多探索.
长江中下游分汇流关系较为复杂,对于其流量频率特征,以往研究多停留在经验频率统计层面[11-12],仅少量研究与理论频率曲线相关. 如陈栋等[13]的分析曾表明国外常用的LN分布不适用于下荆江的有效流量计算. 由于缺乏可用的理论曲线,目前三峡坝下游河道造床流量的计算,更多的是采用基于地貌功原理的图解法[14-15]. 流量频率特征的量化描述以及流量过程蕴含的地貌学信息,都还有待进一步研究. 因此,本文选取长江中下游干流测站,依据三峡水库蓄水前后流量资料开展两方面工作:(1)探索适用于长江中下游流量过程的概率密度函数;(2)应用流量频率曲线分析三峡水库蓄水前后的径流变化及其造床效应. 本文主要关注洪水造床作用,以中洪水期流量频率分析为主.
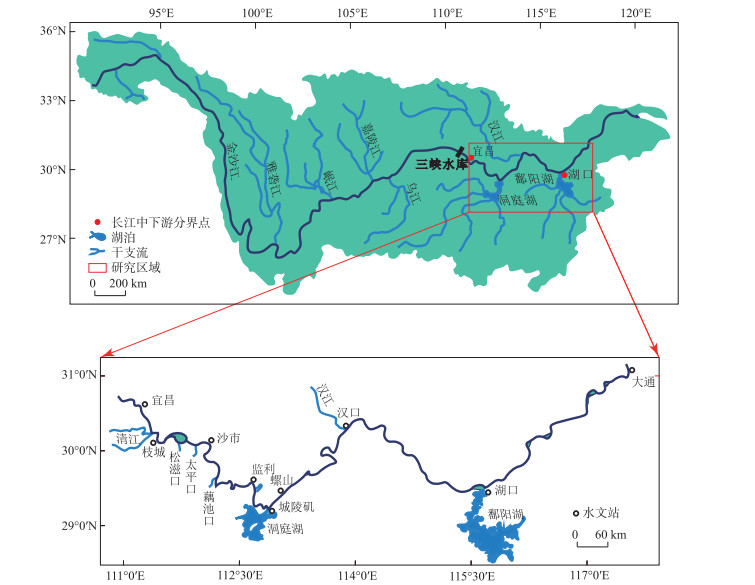
1 研究区域及数据资料 1.1 研究区域长江宜昌至大通段长约1183 km,沿程主要水系及其控制水文站有(图 1):宜昌站控制上游流域面积100万km2;枝城站控制上游来流与清江来水;沙市站控制松滋、太平分流口下游的干流流量;监利站控制下荆江出流;洞庭湖于城陵矶入汇长江后由螺山站控制江湖合流量;汉口站控制汉江入汇口下游流量;大通站为入海流量控制站. 天然情况下(1992—2002年),大通站年径流量约9550亿m3/a,其中宜昌站上游来水占44.8 %,洞庭湖、汉江、鄱阳湖入汇径流分别占30.1 %、3.2 % 和18.8 %. 考虑到清江汛期径流不足宜昌站4 %,且干流冲积河段主要位于枝城站以下,本文主要针对枝城至大通段开展研究.
|
图 1 长江流域及中下游河道概况 Fig.1 The general situation of the Yangtze River basin and river overview in its middle and lower reaches |
研究区域内径流过程受自然与人为双重因素影响. 一方面,长江流域季风性气候显著,表现出降水充沛且汛枯分明的特征. 每年春季南方暖湿气流逐渐向北输送,鄱阳湖水系与洞庭湖水系4—5月份便进入汛期;6—7月份中下游地区梅雨连绵,雨量集中;7—8月上游洪水频发,加之汉江也进入汛期,成为中下游的主汛期;10月以后汛期基本结束. 除特殊年份外,各水系汛期来水先后错开,长江中下游干流洪水历时长且涨落缓慢. 另一方面,位于枝城站上游约102 km的三峡水库于2003年6月开始蓄水,2008年汛后进入175 m试验性蓄水期,每年汛前6月中旬坝前水位降至防洪限制水位145 m,汛末9月中下旬至10月上旬开始蓄水至正常蓄水位175 m,一定程度改变了其下游径流过程[16].
1.2 测站数据及流量过程基本特征本文采用枝城、沙市、监利、螺山、汉口、大通6个水文站逐日平均流量资料,数据来源于长江水利委员会水文局. 为便于对比三峡水库蓄水前后差异,将研究时段划分为2002年前与2004—2019年两个时期. 在三峡水库蓄水前,虽然受下荆江裁弯等影响,长江干流和荆南三口洪道曾发生冲淤调整,对城陵矶以上测站流量产生影响,但这种调整及其造成的影响仅在1990s之前较明显[11, 17]. 为尽可能兼顾水文序列的一致性与代表性,再考虑到各站建站历史等原因,枝城、沙市和监利站的资料统计分别始于1992、1991和1991年,而螺山、汉口与大通站均始于1954年. 通过以上处理,保证了各站资料年限均在10年以上,满足以往造床流量计算研究中对水文序列长度的基本要求[7, 18]. 而三峡水库蓄水后的分析则是假定2004—2019年的水文过程能够稳定持续,由此预判这种流量过程长期作用下的河道变化趋势.
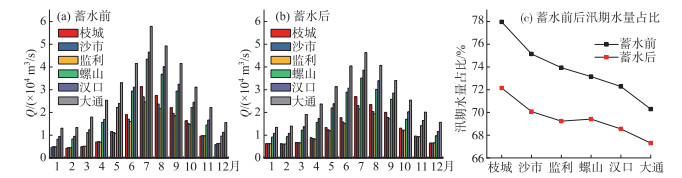
三峡水库蓄水前,长江中下游流量过程汛枯分明,汛期(5—10月)输送全年70 % 以上水量. 从沿程来看,枝城至监利站汛期水量受荆江三口分流影响而减少,至螺山站又因洞庭湖入汇导致水量陡增,螺山站以下因汉江、鄱阳湖等水系汇入沿程水量递增(图 2). 由于江湖调蓄作用,各站年内流量涨落过程沿程坦化. 三峡水库蓄水后,各站年径流量略有减小,受水库“削洪补枯”影响,枝城站汛期水量占全年径流的比例减少约6 %,大通站减少3 %,受影响幅度沿程递减.
|
图 2 三峡水库蓄水前后沿程各站月均流量过程变化(1992—2019年) Fig.2 Variations of monthly average discharge processes before and after impoundment of the Three Gorges Reservoir (1992-2019) |
本文总体研究思路为:首先计算分析三峡水库蓄水前各站流量频率特征,检验多种备选理论曲线的适用性;其次根据流量频率分布特点,分析其中蕴含的河流地貌信息;最后结合三峡水库蓄水后资料,从频率的角度评估流量变化以及由此可能导致的河道调整. 按照以上思路,经验频率统计以及理论频率曲线的类型选取、参数确定与拟合效果检验等是其中的关键环节,对其介绍如下.
2.1 流量频率经验分布统计对于长时期流量序列,各级流量出现频率的计算一般采用分区间统计的模式[18-20]. 考虑到大洪水期流量样本少、跨度大,若汛枯期采用同样间距划分区间,可能会导致频率值跳跃和不连续[19]. 经检验,分别采用对数和算术等间隔方法划分区间,所计算的频率值在大流量区段之外基本重合,而对数等间隔方法的结果在大流量区段更为平滑,因而本文采用对数等间隔方法[7, 19]实施计算. 为尽可能使经验频率连续,对流量区间的数量进行了筛选对比,最终选取为80组. 流量频率统计的具体流程是:首先,根据序列内的最小流量(Qmin)与最大流量(Qmax)值以及分组数80确定各流量区间范围,在对数等间隔下第i级区间左端点
| p\left( {{Q_i}} \right) = \frac{{{N_i}/N}}{{\Delta {Q_i}}}\left( {i = 1, \cdots , 80} \right) | (1) |
式中,p(Qi)为第i级区间对应的概率密度值,Qi为第i级区间的代表流量,Ni/N为第i级流量出现天数占序列总天数的比例,ΔQi为第i级区间的间距;最后,根据p(Qi)与Qi的关系,得到流量频率经验分布.
上述统计步骤中,Qi由区间左右端点值几何平均得到,表示为
| \Delta {Q_i} = {Q_{\min }} \cdot {\left( {\frac{{{Q_{\max }}}}{{{Q_{\min }}}}} \right)^{\frac{1}{{80}}}} - {Q_{\min }} \cdot {\left( {\frac{{{Q_{\max }}}}{{{Q_{\min }}}}} \right)^{\frac{{i - 1}}{{80}}}} = {Q_i} \cdot \left[ {{{\left( {\frac{{{Q_{\max }}}}{{{Q_{\min }}}}} \right)}^{\frac{{0.5}}{{80}}}} - {{\left( {\frac{{{Q_{\max }}}}{{{Q_{\min }}}}} \right)}^{\frac{{ - 0.5}}{{80}}}}} \right] | (2) |
该式表明,对数等间隔下的各区间间距与区间代表值呈正比. 此外,在实际统计过程中,个别站点在上述的考虑下仍出现零频率区间等特殊情况,采取的解决方式是将特殊区间与相邻的后一区间合并,以便保证频率经验分布的连续性[9-10].
2.2 流量频率理论分布曲线类型选取对于非独立的日均连续流量序列的频率分布拟合,归纳了近30年来国内外文献中常用的8种理论分布类型作为备选函数,整理如表 1. 可见,对于以全体流量为对象的频率分布拟合,常用函数的类型大抵可分为正态和伽马两族,其中以对数正态分布最为常见,而伽马族函数尽管也有应用,但相对较少. 对于以中洪水流量为对象的频率分布拟合,可参考的函数类型为指数函数或分段幂函数. 本文拟结合长江中下游流量资料,对表 1中常见理论函数的适用性进行检验,重点考察其对中洪水期频率分布的拟合效果.
| 表 1 常见流量频率理论分布函数* Tab. 1 Common theoretical distribution functions of flow frequency |
表 1中各函数的参数率定难度不同,2个参数的情况可以通过变量转化和回归得到,3个参数的情况以往研究也已颇为丰富,主要通过矩法进行统计确定[5]. 4个参数情况在表 1中仅有分段幂函数(式(10)),Segura等建议采用试算法确定参数[10],其基本思路是:在a1的可能范围(Qmin~Qmax之间)以一定步长设定若干a1值;同样地在α的可能范围(0~1之间)以一定步长设定若干α值;将不同组合的a1和α代入式(10),通过回归分析得到相应a0和β,同时得到拟合优度;如此反复直至所有a1和α组合的遍历,再从中选取拟合优度最好的一组即为最优参数. 该方法实质上是基于经验的试算法,计算量较大. 由于参数a1代表着函数曲线突变的位置,本文根据该特点,采用变量取对数之后的双累积曲线先对a1值进行确定,具体是:基于式(1)算出p(Q)之后,对p(Q)和Q分别取对数,再绘制Σln(p(Q))—Σln(Q)关系曲线,取线性相关性发生突变时的流量作为a1值. 在此基础上再借鉴Segura等的试算法,搭配不同α值通过回归分析得到不同a0和β值,从中选取拟合效果最好的一组作为最优参数.
至于拟合优度的判断,通常采用实测值与拟合函数计算值之间的决定系数为标准[24]. 但考虑到概率的计算误差并非均匀随机分布,而是流量级越大、概率密度越小,其对应的绝对计算误差可能越小. 因此,为缩小大小流量级对应概率密度值之间的悬殊差距,采用下式计算决定系数[24].
| {R^2} = 1 - \frac{{\sum\limits_{i = 1}^n {{{\left( {{\rm{ln}}\left( {p\left( {{Q_i}} \right)} \right) - {\rm{ln}}\left( {f\left( {{Q_i}} \right)} \right)} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left( {{\rm{ln}}\left( {p\left( {{Q_i}} \right)} \right) - {\rm{ln}}\left( {p\left( Q \right)} \right){\rm{ }}} \right)}^2}} }} | (11) |
式中, p(Qi)、f(Qi)分别为第i级流量概率密度的实测值与拟合函数计算值,lnp(Q)为各级流量的实测概率密度对数值取平均,n为流量级数. 显然,拟合效果越好,R2值越接近于1. 基于同样道理,对各级流量下的拟合误差,也以计算与实测概率密度对数值之差来衡量,称为“对数残差”.
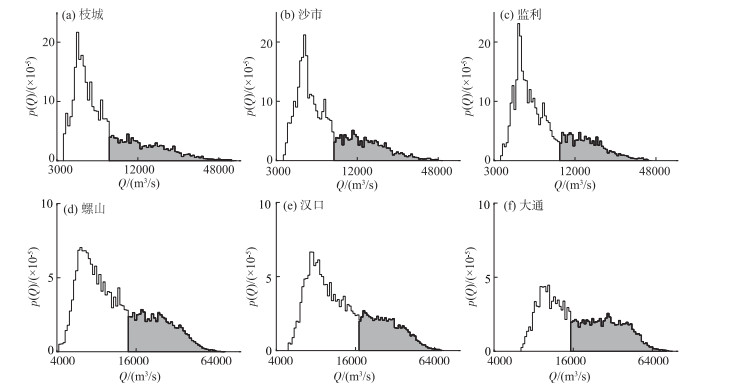
3 三峡水库蓄水前流量频率特征及其地貌意义 3.1 全体流量的频率特征及函数拟合效果由三峡水库蓄水前沿程6站各级流量的频率分布可见(图 3),各站的经验频率分布均属于单峰偏态型,洪枯流量下频率差异显著,表现出一定的分段特征,具体是:在枯水流量段形成“单峰”,中间衔接一“平稳”段,紧接着洪水流量的频率骤降. 沿程来看,这种特点在螺山及其下游各站尤其明显. 相比之下,荆江河段内各站枯水流量段的频率分布更显“高瘦”,中洪水流量级对应的曲线后半段略显低矮,而螺山以下各站的各级流量频率分布逐渐均匀化,大通站尤其明显. 以上特点显然与沿程支流入汇和江湖调蓄导致的基流增大、洪峰坦化等作用有关.
|
图 3 三峡水库蓄水前全体流量的频率分布曲线 Fig.3 Frequency distribution curves of total flow discharge before impoundment of Three Gorges Reservoir |
图 3中各站的流量频率分布均为偏态单峰型,显然不符合表 1中式(3)对应的正态分布. 分别以研究河段进口枝城站和出口大通站为典型代表,检验了式(4)~(8)对应的偏态单峰型理论频率分布函数的适用性. 基于经验频率数据率定参数之后,各理论函数曲线如图 4所示,可见对于偏上游的枝城站,仅有LN3分布能够描述出单峰的位置,但仅是定性符合,整体拟合效果不佳. 其他几类函数对洪水阶段的频率分布拟合较好,但枯水段效果较差. 对于大通站,各类函数整体效果均较差,仅有G函数和P3函数能近似描述洪水阶段的频率分布. 总体来看,表 1中针对全体流量的各类概率密度函数与三峡水库蓄水前的流量频率分布特征明显不符. 这说明,由于枯水流量与中洪水流量频率分布之间较为明显的分段差异性,包括常见的LN分布、P3分布在内,试图用某一函数拟合长江中下游全体流量的整体频率分布特征,难以取得较好效果.

|
图 4 典型站点流量概率密度曲线拟合 Fig.4 Fitting of flow probability density curves at typical hydrological stations |
图 3中的流量频率分布具有明显的分段差异性,基于该特点,以“单峰”段明显结束的位置为界,将数据分为枯水流量段与中洪水流量段两部分,取右端阴影部分进行研究. 经检验,所选取的流量分界值均小于各站累积频率为50 % 的流量以及多年平均流量,因而图 3中各站阴影部分完整包含了所有中洪水流量数据. 以中洪水段的频率数据率定表 1中式(9)、(10)对应的EXP与BPL两种函数参数,并比较它们拟合效果,见表 2和图 5. 除此之外,图 4中显示P3分布也能在洪水阶段取得较好效果,因而表 2和图 5中也包含了P3函数. 对于3个函数拟合效果的比较,利用式(11)计算的R2值作为指标.
| 表 2 三峡水库蓄水前中洪水流量概率密度曲线参数 Tab. 2 Parameters of probability density curves of medium-high flow discharge before impoundment of the Three Gorges Reservoir |
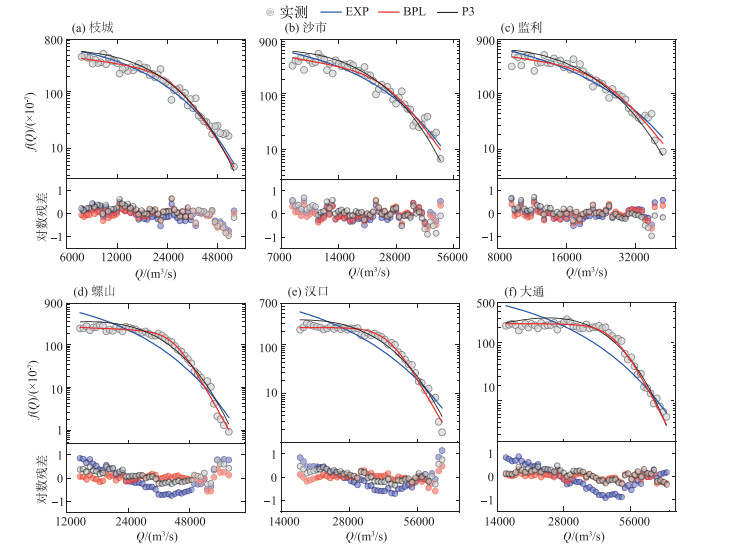
|
图 5 三峡水库蓄水前中洪水流量概率密度曲线 Fig.5 Probability density curves of medium-high flow discharge before impoundment of the Three Gorges Reservoir |
从表 2和图 5中的结果来看,对于监利及其上游各站,EXP与BPL函数效果相对较好,两者的R2值分别在0.93和0.94以上,并且各级流量下的频率对数残差在0附近呈随机波动,而P3函数的R2值在0.92以下. 对于螺山及其下游各站,P3与BPL函数效果相对较好,两者的R2值分别达到0.96和0.98以上,对数残差呈随机波动,而EXP函数的R2值在0.89以下,计算误差明显表现出两端为正、中间为负的系统性偏差特点. 综合来看,BPL函数较好地刻画了各站中洪水流量段“平稳-骤降”式的频率分布特征,螺山站R2值甚至达到0.99左右.
由图 5可看出,式(10)的函数曲线由两段平滑曲线衔接而成,观察式中的参数可见,a1控制了曲线发生转折的临界点,而指数α和β值分别体现了平稳段和骤降段各自的斜率. 通过各站BPL函数曲线的比较,可以在图 3所反映的定性特征基础上,更为定量地反映中洪水流量频率的沿程变化特征. 这种变化特征可由表 2中列出的各站BPL函数参数体现:在监利及其上游各站,a1值沿程减小,而在螺山及其下游各站则沿程增大;荆江河段内各站的α值基本在0.4以上,β值在4~5左右,而螺山及其下游各站的α值在0.2以下,β值在7以上. 以上参数变化体现了监利至螺山站之间的流量频率突变,也说明螺山站下游的流量频率分段特征更为明显.
3.3 流量频率分布特征的地貌意义许多河流上的研究经验表明,冲积河流的中洪水流量频率分布往往受漫滩前后河道槽蓄能力突变的影响,从而表现出明显的转折,借此可以判断河道平滩流量或高程,不同区段的转折点差异能够反映河槽形态沿程变化,这些都具有河流地貌的指示意义[3]. BPL函数较好地描述了流量频率的分段和偏转,因而可以借此解析流量过程与河道形态之间的适应关系.
长江中下游洪水河宽大,洲滩和河漫滩在其中占据较大比例,具有明显的调蓄洪水作用. 除此之外,沿程通江湖泊也具有巨大调蓄洪水和沉积泥沙作用[25],可视为广义上的河漫滩. 但与一般河漫滩不同的是,江湖之间的流量交换集中于分流点和汇流点,分汇点上下游的流量存在突变,也必然导致其频率特性的突变. 从表 2和图 5来看,江湖分汇流的影响体现在以下几点:(1)在监利站以上的江湖分流区,各站的频率分布曲线形态相似,频率随流量增大而逐渐减小,体现了荆江流量主要源于长江上游下垫面产汇流的基本特点,但频率曲线的偏转临界流量a1值沿程减小,又体现了沿程分流导致洪峰坦化的特点;(2)在螺山以下各站,频率分布曲线相比其监利站以上各站发生了较大变化,中水频率“平稳”而大水频率“骤降”,体现了洪源众多、中等量级洪水频发而湖泊调蓄作用导致大流量罕遇的特点;(3)沿程来看,频率曲线的分段特性以及a1值的量级,均在监利与螺山站之间发生突变,而汉口与大通站之间变化相对较小,说明并联型的洞庭湖相比吞吐型的鄱阳湖,对干流洪水流量频率影响更大. 综合来看,洪水流量频率分布受水系结构显著影响而呈现沿程突变,这是罕见于其他河流的独特之处.
地貌功原理[2]认为,某级流量的造床作用由该级流量的输沙能力与持续时间联合决定,流量出现频率是决定其造床作用的重要属性. 基于这一原理,图 5中流量频率的分段特性是否会影响造床流量,是值得研究的问题. 为不失一般性,以冲积河流上普遍存在的幂函数关系[7, 20]来描述长江中下游的输沙率-流量关系,形如Qs=kQm,其中用Qs表示输沙率,k和m为参数. 因此第i级流量造床作用近似表示为Φi≈kQimf(Qi)ΔQi,而对数等间隔下的区间间距ΔQi与区间代表值Qi呈正比,引入式(2)可得:
| {\Phi _i} \approx k\left( {{{\left( {\frac{{{Q_{\max }}}}{{{Q_{\min }}}}} \right)}^{\frac{{0.5}}{{80}}}} - {{\left( {\frac{{{Q_{\max }}}}{{{Q_{\min }}}}} \right)}^{\frac{{ - 0.5}}{{80}}}}} \right)Q_i^{m + 1}f\left( {{Q_i}} \right) | (12) |
将BPL理论频率分布函数式(10)代入,求导得
| {Q_{\rm{e}}} = {a_1}{\left( {\frac{{m + 1 - \alpha }}{{\beta - m - 1}}} \right)^{1/(\beta - \alpha )}} | (13) |
式中参数意义同前. 由该式可见,水文特征对于造床流量的影响反映在密度函数参数a1、α与β上,而输沙特征的影响体现在幂指数m中. 从形式上看,Qe的值可以视为a1和一个修正项的乘积. 表 2中β与α值差距较大,导致式(13)中幂指数1/(β-α)接近于0,因而修正项接近于1,Qe的量级将主要由a1决定. 这意味着当流量频率分布符合BPL函数时,造床流量主要受流量过程影响,与输沙率参数k无关,受幂指数m影响也有限. 为进一步说明该关系,将式(13)对m求导并表达成差分形式可得:
| \frac{{\Delta {Q_{\rm{e}}}}}{{{Q_{\rm{e}}}}} = \frac{{\Delta m}}{{(m + 1 - \alpha )(\beta - m - 1)}} = \theta \Delta m | (14) |
式中, Δm为幂指数m变化量;ΔQe为Δm引起的Qe变化量;θ为α、β、m所决定的系数. 由以往研究经验,大多数平原河流输沙率-流量关系中的m取值在2~3之间[7],考虑到河型影响[26],对以弯曲型为主的荆江河段m近似取2.5,城陵矶以下分汊河段近似取2. 将上述m取值,以及表 2中的各站α与β值代入式(14),可得城陵矶上下游河段的θ分别在0.2附近和0.1以内. 这说明,即使Δm达到0.5的量级,引起的城陵矶上下游河段Qe相对变幅仅在10 % 和5 % 以内.
依据式(13)计算得到的各站地貌功造床流量Qe值如图 6. 为便于比较,图 6中还同时给出了各站的流量频率转折点a1值,以及其他文献中基于资料统计得到的造床流量Qc值[26-27]. 由图可见,虽然三者存在差异,但其量级差别不大. 其中,荆江河段造床流量对应枝城流量30000~35000 m3/s,螺山与汉口站造床流量位于35000~40000 m3/s,大通站造床流量45000 m3/s左右,与这些河段的平滩流量基本相符[11, 27-28]. 该结果一方面证实了所推求造床流量的合理性,另一方面说明了流量频率分段的转折点对造床流量具有决定作用.

|
图 6 三峡水库蓄水前各站特征流量对比 Fig.6 Comparison of characteristic discharges before impoundment of the Three Gorges Reservoir |
国外一些研究[10]中也曾用BPL函数描述流量频率分布,认为漫滩后河道对洪水调蓄作用增强,大流量级被坦化削减,因此流量概率密度曲线发生突变,其转折点a1值近似对应平滩流量. 但对于长江中下游而言,由图 6中监利至螺山站的各特征流量值突变性可见,螺山站以下的造床流量更多地是由其上游江湖关系影响下的频率分布特性所制约.
综上,长江中下游的中洪水流量频率分布和造床流量深受江湖关系影响,BPL型概率密度函数能够较好地描述流量频率分布的分段特征,便于识别造床作用的临界点,为挖掘流量频率蕴含的地貌学信息提供了手段. 这一认识的意义在于,当来流或江湖关系发生调整时,可通过BPL函数量化识别频率变幅,并通过a1值或式(13)来预判流量变化的地貌效应.
4 三峡水库蓄水后流量频率变化及其对造床流量的影响 4.1 三峡水库蓄水前后的流量频率变化图 7中绘制了三峡水库蓄水后沿程各站的流量频率曲线,可见其“单峰-平稳-骤降”的总体频率分布特征仍然显著. 与三峡水库蓄水前相比,各站流量频率分布的变化主要表现为枯水和洪水两端减小,中等流量出现频率增加. 根据水库蓄水前后频率分布曲线的交叉特点,可将变化分为4段,从小到大依次命名为特枯水、枯水、中水与洪水,分别对应图 7中Ⅰ~Ⅳ段,可见4段内的频率变化表现为降低、增加、微增和降低. 统计4段内流量累积频率P(分段内天数占统计年限内总天数的比例)的变化如图 7中各柱形图,可见:城陵矶以上特枯水流量累积频率减小更为明显,平均减幅约19 %;枯水流量累积频率增幅沿程差异不大,均在17 % 附近;中水流量累积频率的增幅,在城陵矶以上约为6 %,城陵矶以下仅为2 %;洪水流量累积频率的减幅,在城陵矶以上约5 %,城陵矶以下约6 %. 从图 7中总体可看出,中洪水频率变化表现为距离大坝越远的位置受影响越小.
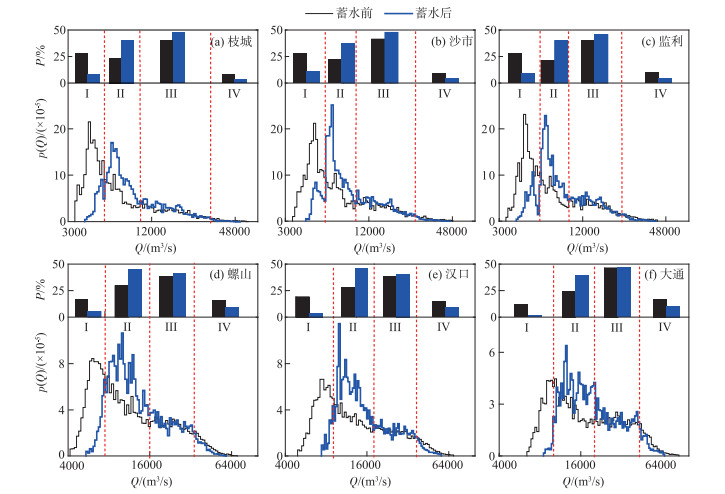
|
图 7 三峡水库蓄水前后流量频率变化 (Ⅰ~Ⅳ分别代表特枯水、枯水、中水和洪水) Fig.7 Changes of flow frequency before and after impoundment of the Three Gorges Reservoir |
采用与上文类似的方法检验了BPL函数在三峡水库蓄水后的适用性,根据经验频率所率定的理论曲线参数见表 3,拟合效果如图 8. 从结果来看,三峡水库蓄水后各站的中洪水流量频率分布仍符合BPL函数曲线,相应的R2值在0.94以上,最大在0.98左右,对数残差散点随机分布在0附近,拟合效果总体良好. 通过三峡水库蓄水前后BPL理论频率分布的参数对比,可反映以下中洪水流量频率变化规律:(1)各站α值有减小趋势,即“平稳”段变得更为平缓,尤其是靠近大坝的荆江河段;(2)螺山及其以上各站β值有所增大,即洪水流量频率骤减的规律更为明显;(3)荆江河段α与β值差距由蓄水前4.5左右上升至5以上,导致中、洪水流量之间的频率分段特征愈发显著,而城陵矶以下α与β差值仍在7.5以上,分段特性依旧明显;(4)沿程各站的分段临界流量a1值有不同程度减小. 总体来看,城陵矶以上变化较大,流量频率分布的分段特性增强,这显然与三峡水库削峰导致流量变幅减小的作用有关. 以BPL函数描述三峡水库蓄水后的频率分布,相比于图 7更为定量地识别了中洪水流量的频率变化特征,也为流量变化之后的地貌效应分析提供了条件.
| 表 3 三峡水库蓄水后中洪水流量概率密度曲线参数及拟合效果 Tab. 3 Parameters of probability density curves of medium-high discharge after impoundment of Three Gorges Reservoir |
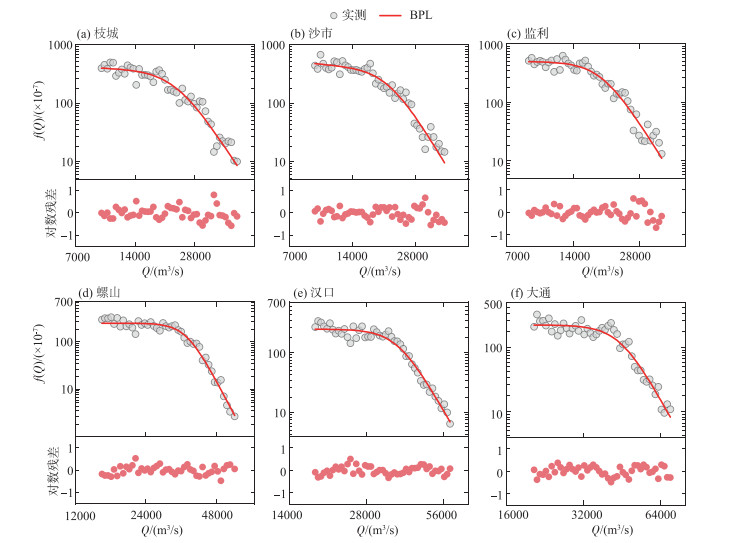
|
图 8 三峡水库蓄水后中洪水流量概率密度曲线 Fig.8 Probability density curves of medium-high flow discharge after impoundment of the Three Gorges Reservoir |
对于冲积河流,来水来沙是塑造河道形态的主动因素,这一特点并不会随水库运行而发生改变. 虽然在建库初期,沙量严重次饱和导致过流断面两侧难以淤积还滩,河道形态与水沙过程之间不相适应,但随着时间推移和出库含沙量增大,河槽必然被重塑,造床流量的概念依然可以用来判断河床调整的总体趋势.
由于三峡水库蓄水后的各站流量频率分布仍符合BPL函数,因而式(13)依然可用. 将表 3中的参数代入式(13),并假设输沙率-流量关系中的幂指数m值保持不变,计算得到各站蓄水后的造床流量如图 9,图中同时给出了蓄水前后的a1值. 由图可见:三峡水库蓄水后的各站a1值发生了不同程度减小,荆江河段减小5000 m3/s,螺山与汉口站减小4500 m3/s,大通站减小3000 m3/s;与a1值的变化相应,各站造床流量也普遍减小,沿程6站的值由蓄水前的33000、30000、27000、37000、39000、45000 m3/s分别减小为蓄水后的26000、22000、20000、33000、35000、42000 m3/s左右. 据此可知,考虑当前阶段的流量频率变化影响,枝城、沙市、监利站造床流量将会分别变为天然情况下的0.79、0.73、0.74倍;螺山、汉口、大通站造床流量将分别变为天然情况的0.89、0.90、0.93倍. 这说明,三峡水库蓄水后,水库调蓄洪水导致大洪水造床的几率减少,长远来看长江中下游河道将有可能发生萎缩,这与国外建坝河流削减洪水之后洪水河槽发生萎缩的规律相一致[29].
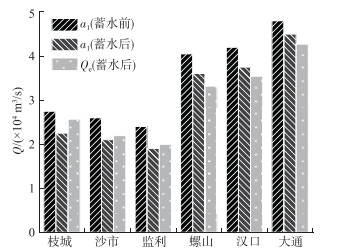
|
图 9 三峡水库蓄水前后坝下各站特征流量对比 Fig.9 Comparison of characteristic discharges of each station before and after impoundment of the Three Gorges Reservoir |
以上计算结果是在假定输沙率-流量关系Qs=kQm中m值变化不大的前提下得到的,但该计算结果仍具备一定的合理性. 一方面,以往大量研究经验已表明,天然河流上的m变幅较小[7, 26],而且近期的观测也证实,三峡水库蓄水后,坝下游同流量下输沙率大幅减小主要是系数k的骤减导致,幂指数m值变化并不大[30]. 另一方面,由式(13)可知系数k对造床流量并无直接影响,式(14)表明m值小幅变化对计算得到的造床流量影响甚小,尤其蓄水后α与β差值愈发加大,m值的影响更小. 因此,即使冲刷过程中输沙率-流量关系不稳定,以上计算仍能够反映长期的河床调整趋势.
根据国内外建坝河流上的经验[16, 29],洪水频率减小之后,河道萎缩的方式有两种:一是滩地淤积导致的洪水河槽形态萎缩;二是河漫滩植被发育和阻力增大导致的行洪能力萎缩. 从三峡水库蓄水后长江中下游干流河道实际变化来看,荆江河段虽然明显下切,但冲刷主要集中于枯水河槽,洪水河槽冲刷较弱甚至个别年份存在淤积[11, 28]. 与此同时,荆江河段内洲滩植被孳生的现象已较为明显[31],对行洪具有潜在不利影响. 在城陵矶以下的分汊河段,界牌、天兴洲、罗湖洲等汊道也因支汊缺乏大洪水塑造,呈现出了明显的“主长支消”调整特征[32]. 以上现象说明,即使在建库初期沙量严重次饱和情况下,流量过程调整已使坝下游洪水河槽呈现了某些萎缩迹象[28],将来随着含沙量逐渐恢复,洪水河槽萎缩的趋向性值得重视.
本文的研究说明,由于长江中下游各站的中洪水频率分布存在分段特性,不同分段内的频率变化将对造床流量产生不同影响,如果流量频率变化导致分段临界点调整,则将引起造床流量变化. 在水库运行过程中,如果能够通过人为调控使流量频率分布的a1值等主要特征量尽量少变或不变,则河道萎缩的趋向性能够缓解或避免. 当然,限于问题复杂性,如何通过水库调控实现这一过程还需进一步分析探索.
5 结论针对长江中下游水文站的日均流量频率分布,检验了多种常用理论概率密度函数的适用性,讨论了流量频率特征与沿程水系分汇、河道形态的联系,从频率角度分析了三峡水库蓄水后的径流变化及其对造床作用的影响. 主要结论有:
1) 三峡水库蓄水前长江中下游各站的流量频率分布表现出“单峰-平稳-骤降”式的分段特性,采用常见的对数正态、皮尔逊Ⅲ型等理论概率密度函数均难以完整描述,但中洪流量的频率分布与分段幂函数符合良好,衡量拟合效果的R2值均在0.94以上. 分段幂函数的参数a1控制曲线发生转折的临界点,指数α和β分别控制平稳段和骤降段各自的变化率. 三峡水库蓄水前,枝城、沙市、监利三站中洪水流量频率分布曲线形态相似,α和β差值较小,a1沿程减小;螺山、汉口、大通三站α和β差值较大,a1沿程增大.
2) 除了枝城以上流域来水特性之外,长江中下游的中洪水流量频率分段特性受沿程河漫滩与通江湖泊等调蓄作用影响明显,在监利与螺山站之间存在突变,这是罕见于其他河流的独特之处. 流量频率分布是影响造床流量大小的重要因素,分段幂函数能够识别出各站流量频率分布的转折点,基于地貌功原理推导的造床流量表达式显示,流量频率分布的转折点与造床流量较为近似.
3) 三峡水库蓄水后各站中洪流量频率仍然符合分段幂函数分布,但其分段特性更为明显,并且临界流量发生不同程度减小. 在输沙率-流量关系中幂指数变化不大的情况下,三峡水库蓄水以来的流量频率变化将导致枝城、沙市、监利站的造床流量变为蓄水前的0.79、0.73、0.74倍,螺山、汉口、大通站的造床流量变为蓄水前的0.89、0.90、0.93倍,说明三峡坝下游洪水河槽存在萎缩的可能性.
| [1] |
Jin GY. A review of hydrologic frequency analysis. Advances in Water Science, 1999, 10(3): 319-327. [金光炎. 水文频率分析述评. 水科学进展, 1999, 10(3): 319-327. DOI:10.3321/j.issn:1001-6791.1999.03.016] |
| [2] |
Wolman MG, Miller JP. Magnitude and frequency of forces in geomorphic processes. Journal of Geology, 1960, 68(1): 54-74. DOI:10.1086/626637 |
| [3] |
Dodov B, Foufoula-Georgiou E. Fluvial processes and streamflow variability: Interplay in the scale-frequency continuum and implications for scaling. Water Resources Research, 2005, 41(5): W05005. DOI:10.1029/2004WR003408 |
| [4] |
Cong SZ, Hu SY. Present situation and prospect of flood frequency analysis. Journal of China Hydrology, 1987(6): 54-60. [丛树铮, 胡四一. 洪水频率分析的现状与展望. 水文, 1987(6): 54-60.] |
| [5] |
Guo SL, Liu ZJ, Xiong LH. Advances and assessment on design flood estimation methods. Journal of Hydraulic Engineering, 2016, 47(3): 302-314. [郭生练, 刘章君, 熊立华. 设计洪水计算方法研究进展与评价. 水利学报, 2016, 47(3): 302-314.] |
| [6] |
Song SB. Research challenges and suggestions of hydrological frequency calculation. Journal of Water Resources and Architectural Engineering, 2019, 17(2): 12-18. [宋松柏. 水文频率计算研究面临的挑战与建议. 水利与建筑工程学报, 2019, 17(2): 12-18.] |
| [7] |
Nash DB. Effective sediment-transporting discharge from magnitude-frequency analysis. Journal of Geology, 1994, 102(1): 79-95. DOI:10.1086/629649 |
| [8] |
Ma YX, Huang HQ, Xu JX et al. Variability of effective discharge for suspended sediment transport in a large semi-arid river basin. Journal of Hydrology, 2010, 388(3/4): 357-369. DOI:10.1016/j.jhydrol.2010.05.014 |
| [9] |
Fennessey N, Vogel RM. Regional flow-duration curves for ungauged sites in Massachusetts. Journal of Water Resources Planning and Management, 1990, 116(4): 530-549. DOI:10.1061/(asce)0733-9496(1990)116:4(530) |
| [10] |
Segura C, Pitlick J. Scaling frequency of channel-forming flows in snowmelt-dominated streams. Water Resources Research, 2010, 46(6): W06524. DOI:10.1029/2009WR008336 |
| [11] |
Xu QX. Study of sediment deposition and erosion patterns in the middle and downstream Changjiang mainstream after impoundment of TGR. Journal of Hydroelectric Engineering, 2013, 32(2): 146-154. [许全喜. 三峡工程蓄水运用前后长江中下游干流河道冲淤规律研究. 水力发电学报, 2013, 32(2): 146-154.] |
| [12] |
Mei XF, Dai ZJ, van Gelder PHAJM et al. Linking Three Gorges Dam and downstream hydrological regimes along the Yangtze River, China. Earth and Space Science, 2015, 2(4): 94-106. DOI:10.1002/2014EA000052 |
| [13] |
Chen D, Yu MH, Zhu YH. Study on effective discharge in the Lower Jingjiang River before and after construction of the Three Gorges Dam. Advances in Water Science, 2018, 29(6): 788-798. [陈栋, 余明辉, 朱勇辉. 三峡建库前后下荆江有效流量研究. 水科学进展, 2018, 29(6): 788-798.] |
| [14] |
Yan JB, Tang QX, Zou T. Variation of dominant discharge and sediment-carrying capacity of flow in the downstream of Three Gorges reservoir. Journal of Yangtze River Scientific Research Institute, 2014, 31(2): 114-118. [闫金波, 唐庆霞, 邹涛. 三峡坝下游河道造床流量与水流挟沙力的变化. 长江科学院院报, 2014, 31(2): 114-118.] |
| [15] |
Zhang W, Gao Y, Xu QX et al. Changes in dominant discharge and their influential factors in the middle and lower reaches of Yangtze River after the Three Gorges Dam impoundment. Advances in Water Science, 2018, 29(3): 331-338. [张为, 高宇, 许全喜等. 三峡水库运用后长江中下游造床流量变化及其影响因素. 水科学进展, 2018, 29(3): 331-338.] |
| [16] |
Zhou JJ, Zhang M. Effect of dams on the regime of the mid-lower Yangtze River runoff and countermeasures. J Lake Sci, 2018, 30(6): 1471-1488. [周建军, 张曼. 近年长江中下游径流节律变化、效应与修复对策. 湖泊科学, 2018, 30(6): 1471-1488. DOI:10.18307/2018.0601] |
| [17] |
Li YT, Guo XH, Tang JW et al. Changes on runoff diversion from Jingjiang reach of the Yangtze River to Dongting Lake after the operation of Three Gorges reservoir. Journal of Basic Science and Engineering, 2009, 17(1): 21-31. [李义天, 郭小虎, 唐金武等. 三峡建库后荆江三口分流的变化. 应用基础与工程科学学报, 2009, 17(1): 21-31.] |
| [18] |
Diedenharn DS, Thorne CR, Soar PJ et al. Effective discharge calculation guide. International Journal of Sediment Research, 2001, 16(4): 445-459. |
| [19] |
Doyle MW, Shields D, Boyd KF et al. Channel-forming discharge selection in river restoration design. Journal of Hydraulic Engineering, 2007, 133(7): 831-837. DOI:10.1061/(asce)0733-9429(2007)133:7(831) |
| [20] |
Goodwin P. Analytical solutions for estimating effective discharge. Journal of Hydraulic Engineering, 2004, 130(8): 729-738. DOI:10.1061/(asce)0733-9429(2004)130:8(729) |
| [21] |
Vogel RM, Kroll CN. Low-flow frequency analysis using probability-plot correlation coefficients. Journal of Water Resources Planning and Management, 1989, 115(3): 338-357. DOI:10.1061/(asce)0733-9496(1989)115:3(338) |
| [22] |
Annable WK, Lounder VG, Watson CC. Estimating channel-forming discharge in urban watercourses. River Research and Applications, 2011, 27(6): 738-753. DOI:10.1002/rra.1391 |
| [23] |
Bunte K, Abt SR, Swingle KW et al. Effective discharge in Rocky Mountain headwater streams. Journal of Hydrology, 2014, 519: 2136-2147. DOI:10.1016/j.jhydrol.2014.09.080 |
| [24] |
Wöhling T, Samaniego L, Kumar R. Evaluating multiple performance criteria to calibrate the distributed hydrological model of the upper Neckar catchment. Environmental Earth Sciences, 2013, 69(2): 453-468. DOI:10.1007/s12665-013-2306-2 |
| [25] |
Wan RR, Yang GS, Wang XL et al. Progress of research on the relationship between the Yangtze River and its connected lakes in the middle reaches. J Lake Sci, 2014, 26(1): 1-8. [万荣荣, 杨桂山, 王晓龙等. 长江中游通江湖泊江湖关系研究进展. 湖泊科学, 2014, 26(1): 1-8. DOI:10.18307/2014.0101] |
| [26] |
Yin XL, Liang ZY, Chen JR et al. River patterns and their changes. Journal of Sediment Research, 1999(2): 15-21. [尹学良, 梁志勇, 陈金荣等. 河型成因研究及其应用. 泥沙研究, 1999(2): 15-21.] |
| [27] |
Xia JQ, Zhou MR, Lin FF et al. Variation in reach-scale bankfull discharge of the Jingjiang Reach undergoing upstream and downstream boundary controls. Journal of Hydrology, 2017, 547: 534-543. DOI:10.1016/j.jhydrol.2017.02.026 |
| [28] |
Li YT, Xue JL, Sun ZH et al. Channel degradation and water level changes in the downstream reach of the Three Gorges Reservoir. Journal of Hydroelectric Engineering, 2021, 40(4): 1-13. [李义天, 薛居理, 孙昭华等. 三峡水库下游河床冲刷与水位变化. 水力发电学报, 2021, 40(4): 1-13. DOI:10.11660/slfdxb.20210401] |
| [29] |
Graf WL. Downstream hydrologic and geomorphic effects of large dams on American rivers. Geomorphology, 2006, 79(3/4): 336-360. DOI:10.1016/j.geomorph.2006.06.022 |
| [30] |
Sun ZH, Zhou WX, Zhou K et al. Relationship between the characteristics of water-sediment transportation in river-lake system and the channel forming discharge of the middle and lower Yangtze River. Journal of Hydraulic Engineering, 2021, 52(5): 521-534. [孙昭华, 周炜兴, 周坤等. 江湖水沙输移与长江中下游造床流量的关系. 水利学报, 2021, 52(5): 521-534.] |
| [31] |
Zhu GL, Li YT, Sun ZH et al. Response of vegetation to submergence along Jingjiang reach of the Yangtze River. PLoS One, 2021, 16(5): e0251015. DOI:10.1371/journal.pone.0251015 |
| [32] |
Han JQ, Zhang W, Yuan J et al. Responses of riverbed morphology to the hydrological regime in anabranching reaches of the downstream Three Gorges Reservoir. Advances in Water Science, 2018, 29(2): 186-195. [韩剑桥, 张为, 袁晶等. 三峡水库下游分汊河道滩槽调整及其对水文过程的响应. 水科学进展, 2018, 29(2): 186-195.] |
 2022, Vol. 34
2022, Vol. 34 


