(2: 聊城大学季羡林学院, 聊城 252059)
(2: Ji Xianlin Honors School, Liaocheng University, Liaocheng 252059, P. R. China)
紊流作为河、湖以及滨海环境中一种常见的水体运动形式,是水体中物质输移的基本动力. 水体的紊动水平直接影响着水体中泥沙、污染物质以及被动标量(对流动不产生影响的标量,如热量、物质浓度场等)的扩散与输移过程[1-2]. 由于紊流条件下水质点运动要素具有随机性与无序性,水体紊动水平通常由统计方法进行表征[3]. 如明渠流条件下,水体紊动强度可由统计理论中瞬时流速的标准差进行表示. 然而,天然状态下河、湖以及滨海环境中水体还常常受到风浪影响,且风浪影响下由水质点周期性运动引起的流速变化通常大于水体紊动带来的流速变化[4-6],单纯计算瞬时流速标准差会明显高估水体紊动强度. 将水质点紊动流速与周期运动进行分离,不仅能够用于受波浪影响水体的紊动分析,进而还有助于研究天然水体中物质、能量的扩散与输移过程.
目前,有关水体波浪—紊动流速分离的方法有很多. Benilov等[7]指出,与水体自由表面波动相关的水质点运动可看做由波浪引起的轨道运动,相反,不相关的水质点运动则是紊动. 利用这一原理,Benilov和Filyushkin通过对水体流速以及水面位移进行同步测量,实现了波浪轨道流速与紊动流速的分离[7]. 然而,该方法需要采用压力传感器或波浪计对水面位移进行同步测量. Trowbridge等同时使用两台流速仪对水体流速进行观测,通过对比两台流速仪的流速数据,认为两者之间存在良好相关性的运动为波浪轨道流速,而相关性较差的则为紊动流速[6, 8]. 然而,这种方法需要使用两台流速仪进行同步观测. 近些年,对于实验室制造的具有单一周期的规则波浪,许多学者采用相位平均法(phase-averaging method)对波浪—紊动流速进行分离[9-11]. 相位平均法通过将瞬时流速的时间序列按照波周期划分为不同的序列段,每个序列段则包含一个完整波形,通过对不同序列段相同相位的瞬时流速进行平均,得到相位平均流速,各序列段瞬时流速与相应相位平均流速的差值则为紊动流速. 然而,相位平均法仅适用于实验室水槽中制造的具有单一周期的规则波浪的紊动流速分离,而自然条件下波浪往往由不同周期、波高以及波长的波浪组成[12],相位平均法不能用于野外条件下水体波浪—紊动流速的分离.
本文根据流速的频谱分布特征提出了一种新的用于水体波浪—紊动流速分离方法,该方法不需要使用压力传感器或波浪计对水面位移进行同步测量,仅需通过一台流速仪对水体流速进行高频测量,便可将水体波浪轨道流速与紊动流速进行分离. 通过验证,该方法对实验室规则波浪条件以及野外不规则波浪条件下水体波浪—紊动流速的分离均具有良好效果.
1 原理与方法波浪作用下,水体瞬时流速u可表示为:
| $ u=U+u_{\mathrm{w}}+u^{\prime} $ | (1) |
式中,U为时均流速,uw为波浪轨道流速,u′为紊动流速. 时均流速为瞬时流速时间序列的算数平均,即:
| $ U=\frac{1}{T} \int_{0}^{T} u(t) \mathrm{d} t $ | (2) |
式中,T为测量时间.
基于频谱分析的水体波浪—紊动流速分离方法(频谱分析法)主要根据瞬时流速的频谱分布特征对流速进行分离. 波浪作用下,瞬时流速的能量谱(power spectral density, PSD)分布中存在明显峰域,该峰域反映了水体波浪信息,且峰域中最大值所对应的频率为波浪主频率,而峰域以外则反映了水体紊动信息. 波浪—紊动流速的分离,主要是在PSD中将反映波浪信息的峰域部分与其余部分进行分离. 具体步骤如下:
1) 对瞬时流速的时间序列值(u(t))进行快速傅里叶变换,得到Fu(f)(f为频率). 不同频率下的信号强度As与相位φ分别表示为:
| $ A_{s}=\sqrt{\left[R\left(F_{u}\right)\right]^{2}+\left[I\left(F_{u}\right)\right]^{2}} $ | (3) |
| $ \varphi=\arctan \left[\frac{I\left(F_{u}\right)}{R\left(F_{u}\right)}\right] $ | (4) |
式中,R(Fu)与I(Fu)分别表示Fu的实部与虚部. 如图 1a所示,信号强度As(f)关于f=F/2(F为流速测量频率)对称. 因此,我们只需对f=0~F/2范围内的频谱进行处理,而后进行对称处理. 在双对数坐标系中绘制As(f)(f=0~F/2)散点图,得到瞬时流速的PSD分布图(图 1b),且PSD中的峰域(图 1b中“+”号所示)反映了水体波浪信息,峰域以外(图 1b中黑色圆点所示)则反映了水体紊动信息.

|
图 1 瞬时流速的能量谱分布((a)为线性坐标系,(b)为双对数坐标系) Fig.1 Power spectral density (PSD) of instantaneous velocity plotted in linear coordinate system (a) and logarithmic coordinate system (b) |
2) 在f=0~F/2范围内,根据PSD中波峰的频域人为设定反映波浪信息的频率范围(波浪窗口),使得波浪窗口涵盖整个峰域. 如图 1b所示,波浪窗口的边界设为fl(低频边界)和fh(高频边界). 此外,选取频率范围(fL~fH),使得该频域包含整个波浪窗口(图 1b).
3) 在双对数坐标系下,对区间(fL~fl)和(fh~fH)内的As进行线性拟合(图 1b中红色直线所示). 在(fl~fh) 范围内,线性拟合得到相应频率下的信号强度At反映了水体紊动信息,拟合线以上部分则反映了波浪信息,且信号强度可表示为Aw=As - At. 波浪窗口以外部分,水体紊动信号强度设为At=As,波浪信号强度设为Aw=0.
4) 假设信号相位角φ不变,确定波浪轨道流速傅里叶参数Fw与紊动流速傅里叶参数Ft:
| $ \begin{aligned} F_{w} =A_{w}[\cos (\varphi)+i \sin (\varphi)] \end{aligned} $ | (5) |
| $ F_{t} =A_{t}[\cos (\varphi)+i \sin (\varphi)] $ | (6) |
5) 对Fw和Ft进行逆傅里叶变换(IFFT),得到波浪轨道流速时间序列uw(t)与紊动流速时间序列u′(t).
根据重建的uw(t)与u′(t),我们采用波浪轨道流速与紊动流速时间序列的标准差分别表征波浪流速大小uw, RMS与紊动强度σ,即:
| $ \begin{gathered} u_{w, R M S}=\sqrt{\frac{1}{T} \int_{0}^{T}\left(u_{w}(t)-\overline{u_{w}}\right)^{2} \mathrm{d} t} \end{gathered} $ | (7) |
| $ \begin{gathered} \sigma=\sqrt{\frac{1}{T} \int_{0}^{T}\left(u^{\prime}(t)-\overline{u^{\prime}}\right)^{2} \mathrm{d} t} \end{gathered} $ | (8) |
式中,
| $ T K E=\frac{1}{2}\left(\sigma_{x}^{2}+\sigma_{y}^{2}+\sigma_{z}^{2}\right) $ | (9) |
式中,σx、σy和σz分别表示3个方向上水体的紊动强度.
2 结果验证与讨论 2.1 实验室数据验证首先,本文将频谱分析法用于实验室水槽中制造的规则波浪的水体波浪—紊动流速分离,并将分离结果与相位平均法进行对比,以验证分离效果. 水槽实验在美国麻省理工学院(MIT)环境流体力学实验室(Nepf Lab)中的波浪水槽中进行. 水槽长24 m,宽0.38 m,高0.38 m;造浪仪安装于水槽最上游位置,它通过液压传动控制桨板前后移动,由程序控制以产生具有特定波高和周期的表面波;水槽最下游有一斜坡(坡度为1 ∶5)以减小波浪反射. 为模拟浅水区波浪,设置2组水深(h)与周期(T)参数(即h=0.4 m、T=2 s以及h=0.45 m、T=1 s). 根据线性波理论中波长(λ)、周期以及水深间的关系(即ω2=(k ·g)tanh(k ·h),其中ω(=2π/T)为角频率,k(=2π/λ)为波数,g为重力加速度),2种设置下波浪波长分别为λ=6.1 m与13.1 m. 采用三维声学多普勒流速仪(ADV,Nortek Vectrino)对水体流速进行高频测量. 测量选用xyz坐标系,其中x为顺水流方向(波浪传播方向),y为横向水流方向,z为垂向水流方向,且3个方向水体瞬时流速可分别表示为ux、uy和uz. 流速垂线剖面测量范围为z=1.3~25.3 cm(z=0表示床底),垂向分辨率为1 cm,测量频率F=200 Hz,单点测量时间6 min. 实验设置详见文献[10].
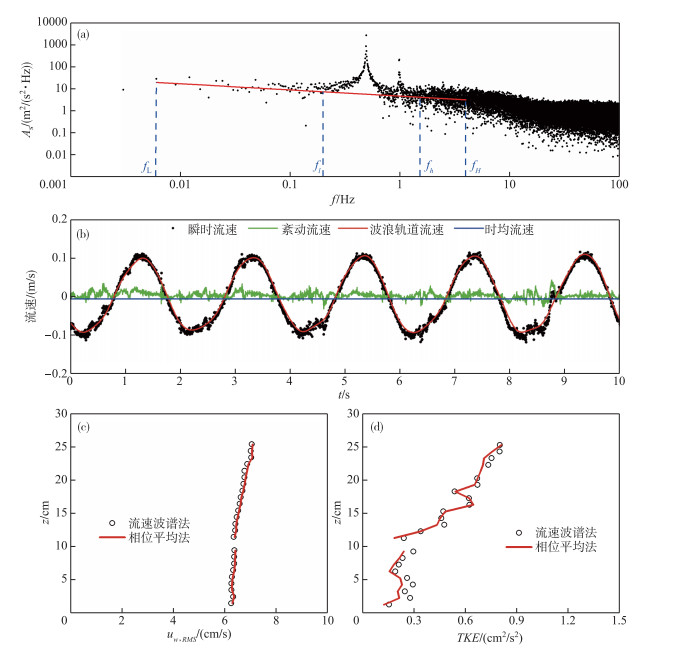
图 2a与b分别给出了文献[10]中S3组次z=24.3 cm处瞬时流速ux的PSD分布以及采用频谱分析法分离后的波浪与紊动流速时间序列. 由于该组次波浪设计周期T=2 s(表 1),ux的频谱分布中在f=0.3~0.7 Hz存在明显峰域,且由于波浪非线性作用的影响,在2倍频率范围f=0.9~1.1 Hz也出现显著能量(图 2a). 为涵盖2个峰域,我们将波浪窗口设置为fl~fh=0.2~1.5 Hz. 按照上文所述步骤对瞬时流速进行分离,瞬时流速(黑色圆点)以及分离后的紊动流速、波浪轨道流速以及时均流速时间序列如图 2b所示. 从图中可以看出,分离后的紊动流速时间序列中不含有水体周期性运动;波浪轨道流速变化平滑,剔除了水体不规则运动.
|
图 2 文献[10]中S3组次z=24.3 cm处瞬时流速ux的PSD分布(a)与分离后的紊动、波浪流速时间序列(b)以及分别采用频谱分析法与相位平均法计算的波浪流速(uw, RMS) 与紊动能(TKE)垂向分布(c, d) Fig.2 PSD of instantaneous velocity (ux) at z=24.3 cm for case S3 in reference [10] (a), time series of the decomposed wave and turbulent velocities (b) and vertical distributions of the wave velocity (uw, RMS, (c)) and turbulent kinetic energy (TKE, (d)) calculated by both the spectral analysis method and the phase averaging method |
为进一步对分离结果进行验证,根据频谱分析法分离后波浪与紊动流速的时间序列,采用式(7)与式(9)分别计算x方向上的波浪流速(uw, RMS)以及水体紊动能(TKE),并与相位平均法计算结果进行对比. 图 2c与d分别给出了组次S3采用2种方法计算得到的uw, RMS与TKE的垂线分布图. 从图中可以看出,对uw, RMS与TKE而言,全水深范围内频谱分析法(圆圈所示)与相位平均法(红色实线所示)计算结果吻合较好. 以相位平均法计算结果为基准,两种方法对uw, RMS与TKE的计算差异在全水深范围内分别控制在1 % 与25 % 以内,全水深平均差异分别为0.6 % 和11.7 % (表 1). 此外,我们利用2种方法对文献[10]中其他无植被组次(S1~S2、S4~S8)以及部分含植被组次(A3、B3、C3与D3,植被设置以及流速测量位置详见文献[10])的uw, RMS与TKE进行了计算,各组次2种方法计算结果的全水深平均差异如表 1所示. 对所有无植被组次而言,频谱分析法与相位平均法计算结果差异较小,uw, RMS与TKE差异分别控制在1 % 与20 % 以内,且随着全水深平均波浪流速
| 表 1 水槽实验各组次波浪参数信息以及频谱分析法与相位平均法计算下的波浪流速(uw, RMS) 与紊动能(TKE)的差异 Tab. 1 Wave parameters for each flume experimental scenario and deviations of uw, RMS and TKE between calculations using spectral analysis method and phase-averaging method |
野外观测在东平湖(山东)展开. 东平湖是我国南水北调工程东线的主要调节湖泊以及山东省西水东调的水源地,由于北部出湖口受闸门控制,湖泊水体运动主要受风浪影响. 选择风力较大天气,采用声学多普勒流速仪(ADV,Nortek Vector)对水体流速进行定点测量. 测量时水深h=2.55 m,流速测量位置距床底15 cm处,测量频率为F=64 Hz,单点测量时间为T=5 min. 测量选用ENU坐标系统,且在ENU坐标系下,水质点在正东(E)、正北(N)以及垂直向上(U)方向上的流速可表示为ue、un和uu.
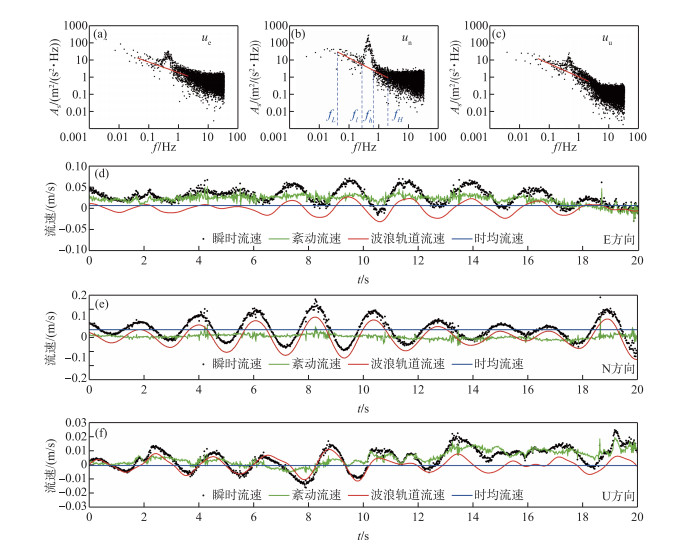
3个方向瞬时流速的PSD如图 3a~c所示. 从图中可以看出,ue、un和uu的频谱分布中均存在明显峰域,峰域中信号强度最大值对应频率为0.5 Hz,波浪主周期T=2 s. 根据线性波理论,此次测量过程中波浪波长λ=13.0 m,且由于λ>2 h,波浪为浅水波. 由于峰域对应的频率范围为0.3~0.7 Hz,我们将波浪窗口的边界设为fl~fh=0.3~0.7 Hz. 图 3d~f分别给出了3个方向瞬时流速(黑色圆点所示)、波浪轨道流速(红色实线)、紊动流速(绿色实线)以及时均流速(蓝色实线)的时间序列. 从图中可以看出,分离后的波浪流速剔除了水体脉动成分,变化平滑,反映了水体的周期性运动;紊动流速时间序列中去除了低频的周期变动,反映了水体脉动变化. 由于波浪为浅水波,且流速测量位于近床底处,水质点运动受床底影响而发生扭曲,使得测量处水质点运动轨迹扁平,水平方向波浪轨道流速(如N方向uw=-0.1~0.1 m/s,图 3e)明显大于垂向波浪流速(如U方向uw=-0.01~0.01 m/s,图 3f). 波浪轨道流速的差异,使得三个方向瞬时流速的频谱分布存在差异,其中un的峰域强度最大,uu的峰域强度最小,且较小的波浪流速使得uu的波浪—紊动流速分离效果在3个方向流速中较差.
|
图 3 3个方向瞬时流速PSD分布图(a~c)以及分离后的流速时间序列(d~f) Fig.3 of instantaneous velocity in three directions (i.e., subplots (a-c)) and time series of the instantaneous velocity and the wave-turbulent velocity after decomposition (i.e., subplots d~f) |
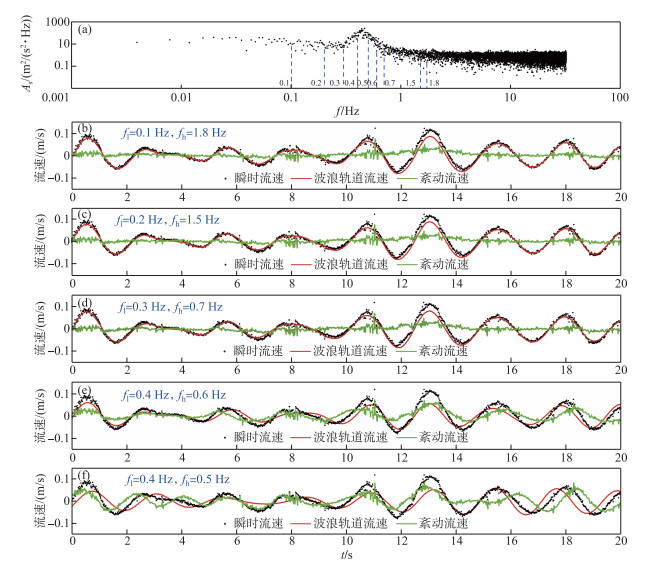
根据流速分离步骤,采用频谱分析法对水体波浪—紊动流速分离过程中需要设置波浪窗口. 然而,通常情况下波浪窗口界限模糊,使用者往往不能够对其边界进行准确确定. 为研究不同波浪窗口频域设置对分离结果的影响,以野外实验中瞬时流速un的时间序列为例,通过设置5组波浪窗口频域对瞬时流速进行分离. 5组波浪窗口频域自宽向窄依次设置为fl~fh=0.1~1.8、0.2~1.5、0.3~0.7、0.4~0.6以及0.4~0.5 Hz. 如图 4a所示,组次0.4~0.6与0.4~0.5 Hz的窗口频域设置均明显位于峰域内部,其余3个组次的频域设置均位于峰域外部,即组次0.4~0.6与0.4~0.5 Hz波浪窗口的频域设置并没有完全包含整个峰域. 各频域设置下,瞬时流速以及分离后的波浪流速和紊动流速如图 4b~f所示. 为更好地展示分离效果,对瞬时流速时间序列进行去均值化,即图 4b~f中瞬时流速的时均值为0. 从图中可以看出,当频域设置位于峰域外部时(图 4b~d),分离后的紊动流速时间序列中不再含有水体低频的周期运动,分离效果较好;当频域设置位于峰域以内时(图 4e~f),分离后的紊动流速时间序列中仍然含有周期性变化,流速分离效果较差,且频域设置范围越小,分离效果越差. 对比组次0.1~1.8、0.2~1.5以及0.3~0.7 Hz分离后的波浪轨道流速时间序列,3种设置下波浪轨道流速差异在0.5 % 以内,故当波浪窗口频域设置位于峰域以外时,不同的频域设置对分离结果影响较小. 因此,在波浪窗口的频域设置中,频域设置应明显位于峰域以外,以获取最佳的分离效果.
|
图 4 不同波浪窗口频域设置及其分离后的流速时间序列 Fig.4 Different frequency-domain settings for wave window and the velocity time series after decomposition using different settings |
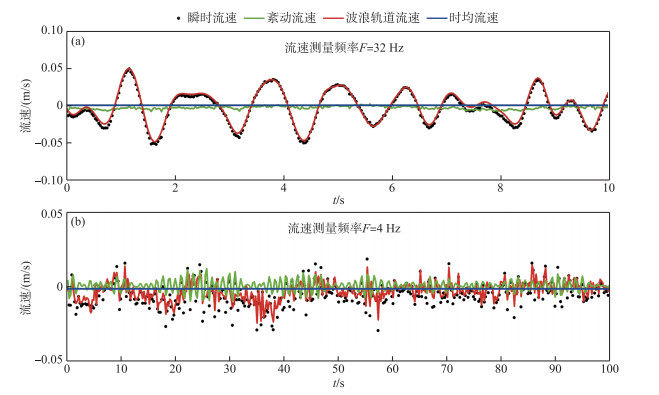
为研究流速测量过程中测量频率对分离效果的影响,设置2种较低采样频率(F=32、4 Hz)对野外条件下的水体流速进行测量,并分别采用频谱分析法对水体波浪流速与紊动流速进行分离. 2种采样频率设置下水体的瞬时流速、波浪流速、紊动流速以及时均流速如图 5所示. 从图中可以看出,当F=32 Hz时,频谱分析法仍能对波浪—紊动流速进行有效分离(图 5a). 然而,当流速测量频率较小时(如F=4 Hz),瞬时流速不能准确反映水体脉动信息,频谱分析法对流速的分离效果较差(图 5b). 因此,采用频谱分析法对波浪—紊动流速进行分离时,应采用流速仪对水体流速进行高频测量才能获取最佳分离效果.
|
图 5 不同流速测量频率下采用频谱分析法对水体波浪—紊动流速的分离结果 Fig.5 Results of the wave-turbulent velocity decomposition using spectral analysis method under different sampling-rate settings |
为对天然条件风浪作用下的水体紊动进行分析,本文根据瞬时流速频谱分布特征,提出了一种水体波浪—紊动流速分离方法,且该方法仅需通过一台流速仪对水体流速进行测量,便可实现对波浪流速与紊动流速的分离. 本文给出了基于频谱分析的水体波浪—紊动流速分离方法的具体实施步骤,并分别采用实验室水槽数据以及野外实验数据对该方法的分离效果进行验证. 验证结果表明,频谱分析法不仅能够用于实验室中规则波浪条件下水体波浪—紊动流速的分离,还能够对野外不规则波浪条件下水体流速进行分离. 本文采用文献[10]中无植被组次以及部分含植被组次的水槽实验数据,利用频谱分析法以及相位平均法分别计算水体波浪流速(uw, RMS)与紊动能(TKE),并进行对比分析. 分析结果显示,对所有组次而言,2种方法对uw, RMS与TKE计算结果的平均差异分别控制在1 % 和20 % 以内,且随着波浪流速以及紊动能的增加,2种计算方法间的差异逐渐减小. 波浪窗口的频域设置是分离过程中的关键步骤,本文通过不同的波浪窗口频域设置研究了频域设置对分离效果的影响. 结果表明,当频域设置位于峰域以外时,频谱分析法能够对波浪—紊动流速进行有效分离,且频域大小对流速分离结果影响较小;当频域设置明显位于峰域以内时,频谱分析法对流速的分离效果较差. 此外,流速测量频率对流速分离效果产生影响. 当流速测量频率较低时,瞬时流速不能反映水体紊动信息,频谱分析法不能对波浪—紊动流速进行有效分离.
| [1] |
Murphy E, Ghisalberti M, Nepf H. Model and laboratory study of dispersion in flows with submerged vegetation. Water Resources Research, 2007, 43(5): W05438. DOI:10.1029/2006WR005229 |
| [2] |
Nepf HM. Flow and transport in regions with aquatic vegetation. Annual Review of Fluid Mechanics, 2012, 44(1): 123-142. DOI:10.1146/annurev-fluid-120710-101048 |
| [3] |
Zhao ZX, He JJ. Hydraulics(Second Edition). Beijing: Tsinghua University Press, 2010. [赵振兴, 何建京. 水力学(第2版). 北京: 清华大学出版社, 2010.]
|
| [4] |
Jiang JY, Street RL. Modulated flows beneath wind-ruffled, mechanically generated water waves. Journal of Geophysical Research: Oceans, 1991, 96(C2): 2711-2721. DOI:10.1029/90JC02259 |
| [5] |
Thais L, Magnaudet J. A triple decomposition of the fluctuating motion below laboratory wind water waves. Journal of Geophysical Research: Oceans, 1995, 100(C1): 741-755. DOI:10.1029/94JC02714 |
| [6] |
Trowbridge JH. On a technique for measurement of turbulent shear stress in the presence of surface waves. Journal of Atmospheric and Oceanic Technology, 1998, 15(1): 290-298. DOI:10.1175/1520-0426(1998)0150290:oatfmo>2.0.co;2 |
| [7] |
Benilov YA, Filyushkin BN. Application of methods of linear filtration to an analysis of fluctuations in the surface layer of the sea. 1970.
|
| [8] |
Shaw WJ, Trowbridge JH. The direct estimation of near-bottom turbulent fluxes in the presence of energetic wave motions. Journal of Atmospheric and Oceanic Technology, 2001, 18(9): 1540-1557. DOI:10.1175/1520-0426(2001)0181540:tdeonb>2.0.co;2 |
| [9] |
Luhar M, Coutu S, Infantes E et al. Wave-induced velocities inside a model seagrass bed. Journal of Geophysical Research: Oceans, 2010, 115(C12): C12005. DOI:10.1029/2010JC006345 |
| [10] |
Zhang YH, Tang CH, Nepf H. Turbulent kinetic energy in submerged model canopies under oscillatory flow. Water Resources Research, 2018, 54(3): 1734-1750. DOI:10.1002/2017WR021732 |
| [11] |
Tang CH, Lei JR, Nepf HM. Impact of vegetation-generated turbulence on the critical, near-bed, wave-velocity for sediment resuspension. Water Resources Research, 2019, 55(7): 5904-5917. DOI:10.1029/2018WR024335 |
| [12] |
Toffoli A, Bitner-Gregersen EM. Types of ocean surface waves, wave classification. New Jersey: John Wiley & Sons, Ltd, 2017. DOI:10.1002/9781118476406
|
 2022, Vol. 34
2022, Vol. 34 

