(2: 四川大学水力学与山区河流开发保护国家重点实验室, 成都 610065)
(3: 成都大学建筑与土木工程学院, 成都 610106)
(2: State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, P. R. China)
(3: College of Architecture and Civil Engineering, Chengdu University, Chengdu 610106, P. R. China)
温室气体主要包括二氧化碳(CO2)、甲烷(CH4)和氧化亚氮(N2O)等[1]. 化石燃料能源的利用、森林的砍伐、人工湿地的形成和畜牧业的大规模发展等人类活动会显著增加大气中的温室气体浓度,引起地球平均温度的升高从而导致全球气候变暖,对人类生产和生活带来了巨大的负面影响[2-4]. 水力发电将天然水体的势能和动能转化为电能输出,可大幅减少CO2、CH4等温室气体的排放量,是迄今唯一技术已发展成熟、可大规模开发的再生能源. 然而,筑坝蓄水将不可避免地淹没一定数量的土地,改变水文情势,迫使原有区域生态系统同大气之间温室气体的源汇关系发生变化[5]. 水库温室气体源汇变化是近年来水利水电工程开发和运行的重要关注问题之一.
目前,水库温室气体排放的主要途径有:1)水库库区与下游受影响河道水—气界面扩散释放;2)近岸浅水区域可能出现的气泡释放;3)库岸带或水库消落带的温室气体排放;4)水体流经大坝(包括泄流建筑物及水轮机组等)时,因压力和温度的瞬间改变,导致温室气体产生消气释放(degassing). 不同的水库在不同季节和运行方式下的消气释放通量存在明显的时空异质性[6],其对水库温室气体总排放量的贡献亦有显著差别. 已有研究发现,水库CO2的消气释放量可占到其运行期间CO2总排放量的3.28 % ~57.14 %;而CH4的消气释放量可占到水库CH4总排放量的2.05 % ~51.89 % [7-10]. 尽管如此,当前全球水库温室气体消气释放的研究仍十分有限. 另一方面,当前水库温室气体消气排放估算中,多将水库视为一个整体,在临近大坝的上下游设置控制断面,结合两个控制断面间的浓度差和流量变化进行估算. 由于温室气体在过坝下泄过程(泄洪)与在发电设施中的释放机理并不相同,当前的水库温室气体消气释放研究,鲜有对这两种消气释放方式分别予以考虑.
本研究拟针对溶解态温室气体在过坝下泄中的传质和输运过程进行数值模拟分析,以大渡河铜街子电站和瀑布沟电站为例,针对典型泄洪工况,模拟计算温室气体在溢流坝面和空中挑射过程中及坝下水垫塘或消力池内的浓度变化及排放速率,为明确不同泄洪方式下的温室气体消气释放强度、准确核算水库不同服务功能下温室气体排放速率提供新的研究思路和方法基础.
1 计算模型的建立目前国内外尚未有关于温室气体过坝下泄数值模拟研究的报道,而四川大学、清华大学及美国爱荷华大学等机构对总溶解气体和溶解氧的过坝下泄过程进行了卓有成效的数值模拟研究[11-13]. 本研究基于Yang等[14]建立的关于总溶解气体的立面二维气液两相流模型,在已有模型的基础上,考虑CO2、CH4等温室气体的理化性质,增加了温室气体排放速率计算公式,建立了温室气体过坝下泄排放速率计算模型.
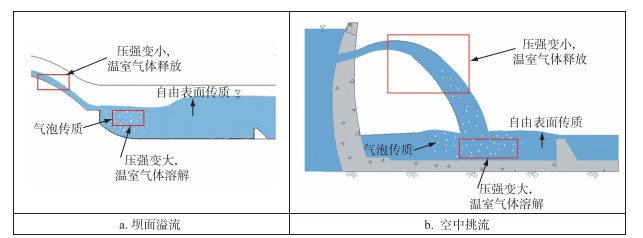
1.1 模型结构Yang等[14]提出气体在水气界面的传质可分为气泡界面传质和水气自由表面传质. 水坝泄水时,水流在溢流坝面或空中挑射的过程中,由于压力的瞬间改变,水体中温室气体的溶解度降低,部分温室气体将以气泡的形式从水中析出;在坝下,大量的空气被泄洪水流卷吸进入水中,并在水中形成大量气泡,当气泡流至坝下消力池或水垫塘底部时,由于消力池和水垫塘内气体的承压急剧增大,气体溶解度较常压下显著增加,导致温室气体通过气泡传质从气泡溶解进入水中. 此外,在自由液面还存在溶解态温室气体与大气之间的传质发生过程,温室气体过坝下泄的传质过程如图 1所示.
|
图 1 温室气体过坝下泄传质过程示意图 Fig.1 Mass transfer process of GHG with discharge |
温室气体排放速率计算模型通过VOF(volume of fluid)气液两相流模型计算自由液面,采用RANS (Reynolds-averaged Navier-Stokes)紊动模型进行求解.
模型的连续性方程和动量方程由以下公式表示:
| $ \nabla \cdot \boldsymbol{U}=0 $ | (1) |
| $ \frac{{\partial (\rho \cdot U)}}{{\partial t}} + \nabla \cdot (\rho \cdot \mathit{\boldsymbol{U}} \cdot \mathit{\boldsymbol{U}}) = - \nabla P + \nabla \cdot (\mu \cdot \nabla \mathit{\boldsymbol{U}}) + \rho \cdot {\mathit{\boldsymbol{f}}_{\rm{b}}} $ | (2) |
| $ \frac{\partial \alpha}{\partial t}+\nabla \cdot(\boldsymbol{U} \cdot \alpha)=0 $ | (3) |
| $ \rho=\rho_{\mathrm{w}} \cdot \alpha_{\mathrm{w}}+\rho_{\mathrm{g}}\left(1-\alpha_{\mathrm{n}}\right) $ | (4) |
| $ \mu=\mu_{\mathrm{w}} \cdot \alpha_{\mathrm{w}}+\mu_{\mathrm{g}}\left(1-\alpha_{\mathrm{w}}\right) $ | (5) |
式中,ρ为水气混合密度(kg/m3),根据水气两相体积分数加权计算得到,见式(4);μ为动力粘度(kg/(m ·s));fb为考虑了重力和表面张力的相间表面上的单位质量上的体积力(m/s2),P为压强(Pa). α为体积分数;下标w表示水相;下标g表示气相.
模型采用标准k-ε紊流模型,相关方程如下:
| $ \frac{\partial(\rho k)}{\partial t}+\nabla \cdot(\rho k U)=\frac{\partial}{\partial x_{j}}\left[\left(\mu+\frac{\mu_{\mathrm{t}}}{\sigma_{k}}\right) \frac{\partial k}{\partial x_{j}}\right]+G_{k}-\rho \varepsilon $ | (6) |
| $ \frac{\partial(\rho \varepsilon)}{\partial t}+\nabla \cdot(\rho \varepsilon U)=\frac{\partial}{\partial x_{j}}\left[\left(\mu+\frac{\mu_{t}}{\sigma_{\varepsilon}}\right) \frac{\partial \varepsilon}{\partial x_{j}}\right]+\frac{C_{1 \varepsilon} \varepsilon}{k} G_{k}-C_{2_{\varepsilon}} \rho \frac{\varepsilon^{2}}{k} $ | (7) |
式中,k为紊动动能(m2/s2);ε为紊动动能耗散率(m2/s3);μt为紊流粘性系数(kg/(m ·s));Gk为由平均速度梯度引起的紊动动能产生项(kg/(m ·s3));σk为紊动能所对应的Prandtl数;σε为紊动能耗散率所对应的Prandtl数;C1ε、C2ε分别为紊流模型计算参数.
1.3 温室气体输移扩散方程因过坝下泄消气释放过程时间短,忽略温室气体在水体中发生的电化反应和可能存在的生物转化,通用的温室气体浓度输移扩散方程为:
| $ \frac{\partial C}{\partial t}+\nabla \cdot(\boldsymbol{U} C)=\nabla \cdot\left[\left(\nu_{\mathrm{m}}+\frac{\nu_{\mathrm{t}}}{S c}\right) \nabla C\right]+S_{\mathrm{b}}+S_{\mathrm{s}} $ | (8) |
式中,C为某种温室气体在水中的浓度(mol/m3);Sc为Schmidt数;νt为紊动扩散系数(m2/s);νm为分子扩散系数(m2/s);Sb为气泡溶解于水中或从水中析出的温室气体浓度源项(mol/(m3 ·s));Ss为水气自由界面传质源项(mol/(m3 ·s)).
1.3.1 气泡传质源项目前已有相关研究对气泡的界面传质进行了分析[15-16],本研究采用的气泡传质源项计算公式如下:
| $ S_{\mathrm{b}}=f \frac{6 \alpha_{\mathrm{g}} \cdot k_{\mathrm{b}}}{D_{\mathrm{b}}}\left[C_{\mathrm{atm}}\left(1+\frac{P}{P_{\mathrm{atm}}}\right)-C\right] $ | (9) |
式中,Catm为在对应当地大气压和当时温度条件下该气体的饱和溶解度(mol/m3);P、Patm分别为压强和标准大气压(Pa);Db为气泡粒径(m);f为某种温室气体在空气中的组分比例;kb为紊动气泡界面传质系数(m/s).
| $ k_{\mathrm{b}}=\beta \frac{2 \nu_{\mathrm{m}} \cdot P e_{\mathrm{b}}^{1 / 2}}{\sqrt{\pi} D_{\mathrm{b}}}\left(1-\frac{2}{3\left(1+0.09 R e_{\mathrm{b}}^{2 / 3}\right)^{3 / 4}}\right) $ | (10) |
| $ R e_{\mathrm{b}}=\frac{\rho_{\mathrm{w}} \cdot D_{\mathrm{b}}\left|\boldsymbol{U}_{\mathrm{br}}\right|}{\mu_{\mathrm{w}}} $ | (11) |
| $ P e_{\mathrm{b}}=D_{\mathrm{b}}\left|\boldsymbol{U}_{\mathrm{br}}\right| / \nu_{\mathrm{m}} $ | (12) |
式中,β为模型参数,需通过率定得到;Reb为气泡雷诺数;Peb为气泡Peclet数;Ubr为气泡相对运动速度(m/s);μw为水相动力粘度(kg/(m·s)).
1.3.2 自由表面传质源项| $ S_{\mathrm{s}}=\frac{k_{1}}{\Delta Z}\left(C_{\mathrm{atm}}-C\right) $ | (13) |
式中,ΔZ为表层网格高度(m);kl为自由表面传质系数(m/s)[17].
| $ k_{1}=k_{600}\left(\frac{S c_{\mathrm{b}}}{600}\right)^{-x} $ | (14) |
式中,x为常数,取值受风速影响;k600是在20℃时Schmidt常数等于600的气体传输速度(m/s);Scb为温室气体的Schmidt常数,取决于温度高低.
对于CO2和CH4有:
| $ \begin{aligned} S c_{\mathrm{b}}\left(\mathrm{CO}_{2}\right) &=1911.1-118.11 t+3.4527 t^{2}-0.04132 t^{3} \end{aligned} $ | (15) |
| $ S c_{\mathrm{b}}\left(\mathrm{CH}_{4}\right) =1897.8-114.28 t+3.2902 t^{2}-0.039061 t^{3} $ | (16) |
式中,t为温度(℃),本研究采用温室20℃进行计算.
1.4 温室气体排放速率方程| $ E=Q \cdot \Delta C $ | (17) |
式中,E为温室气体向大气中的排放速率(mol/s);Q为水流流量(m3/s);ΔC为上下游断面温室气体浓度差(mol/m3).
1.5 数值求解本研究基于OpenFOAM开源平台开展模拟求解,以interFoam求解器为基础,在计算流场、压力场的基础上添加温室气体浓度输运方程,以PIMPLE算法反映压力变化对速度场的影响. PIMPLE算法将SIMPLE (Semi-Implicit Method for Pressure-Linked Equations)算法和PISO (Pressure Implicit with Splitting of Operators)算法结合起来,PIMPLE的基本思想是在每个时间步长内用SIMPLE稳态算法求解,时间步长的步进用PISO算法来完成. 在方程离散格式上,瞬时项采用Euler格式;对流项采用Gauss linear格式;拉普拉斯项使用Gauss linear corrected格式. 具体信息详见https://openfoam.org.
2 温室气体过坝下泄模拟本研究分别考虑了坝面溢流和空中挑流2种情况. 在坝面溢流过程中,由于水流发生自掺气而形成掺气水流. 掺气水流增大了气液接触面积,同时也改变了流场和压力分布,从而促进了气液传质. 而空中挑流则是将水流射向空中形成挑流状态,水流完全暴露在大气中从而发生掺气. 在空中挑流情况下,气液传质受到水流破碎程度的影响.
2.1 坝面溢流温室气体浓度分布:以铜街子电站泄流工况为例采用大渡河铜街子水电站作为典型坝面溢流研究对象. 铜街子水电站位于大渡河梯级开发的下游河段,如图 2所示. 大坝为混凝土重力坝,最大坝高82 m,总库容2.0亿m3,调节库容0.3亿m3,为日、周调节水库. 溢流坝段全长105 m,分5个等宽坝块,每个坝块设以开敞式溢流表孔. 铜街子工程泄水采用底流消能形式,在桩号(坝)0+160.0 m处设置消力坎,并在护坦末端设置差动式尾坎,起到二次消能的作用.

|
图 2 铜街子水电站泄水照片 Fig.2 The picture of Tongjiezi Dam |
四川大学于2009年对铜街子电站的坝下过饱和总溶解气体进行了原型观测,采用原型观测工况,即铜街子水电站3#溢流表孔泄水时作为计算工况,对应泄水流量为629 m3/s,上下游水位差为33.65 m. 根据以往针对长江上游梯级水库的温室气体浓度的实测资料可知,长江上游梯级库区中的溶解态CO2、CH4基本处于过饱和状态,因此,本研究设计了4组计算工况,如表 1所示,CO2、CH4的上游来流饱和度范围分别为100 % ~180 %,各工况下的CO2和CH4的初始饱和度均为100 %. 为便于对比分析,本研究引入了气体饱和度,其计算公式为:
| $ G=\frac{C}{C_{\mathrm{atm}}} \times 100 \% $ | (18) |
| 表 1 铜街子/瀑布沟电站计算工况设置 Tab. 1 Settings of calculate working conditions of Tongjiezi/Pubugou Dam cases |
式中,G为温室气体的饱和度(%).
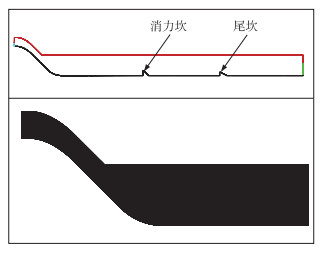
2.1.2 网格划分及边界条件计算区域纵向范围从铜街子坝前到坝下约360 m. 计算区域采用2D结构化网格. 鉴于掺气浓度对网格尺寸要求较高,在进行网格划分时,着重对水气交界面进行加密处理. 该区域网格密度较大,网格尺寸大小仅0.2 m左右,在其他区域纵向和垂向上,网格尺寸大小在0.5~1.5 m之间. 铜街子电站计算区域网格划分及边界设置示意图见图 3.
|
图 3 铜街子电站计算边界及网格划分示意图 (红色:空气入流;绿色:出流;蓝色:速度入流;黑色:固壁) Fig.3 The boundary condition and mesh of Tongjiezi Dam cases |
Yang等[14]根据原型观测结果分别对铜街子电站的坝下总溶解气体饱和度分布进行模型参数率定和验证. 结果表明,当气泡粒径均值取0.005 m,模型参数β为3.0时,铜街子电站的坝下总溶解气体饱和度的计算值与实测值的误差在5 % 以内. 模拟结果表明,在此模型参数取值情况下,该模型可以很好地模拟出过坝下泄过程中的气液传质过程和溶解气体浓度分布.
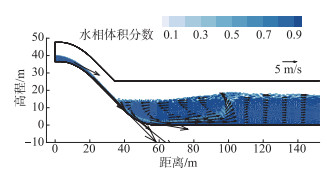
2.1.4 模拟结果分析图 4为铜街子电站计算工况泄水时水相体积分数分布及速度矢量图. 可以看出,下泄水流进入到消力池内造成了大量气泡卷吸入水体中,导致消力池内掺气浓度升高. 从流速矢量图可以看出,水流从溢流坝下泄至消力池时,下泄水流与消力池中的水体发生强烈碰撞,消力池内流速急剧增大,其中高流速的主流在消力池底部,最大流速达19 m/s. 在水体潜入消力池底部过程中,由于受到水体阻力,小部分水体向上冲击形成较大漩涡,大部分主流水体流向下游,通过水跃产生表面旋滚和强烈紊动,起到卷吸空气进入水体并消能的作用.
|
图 4 铜街子电站自由液面及速度矢量示意 Fig.4 The free surface and velocity vector of Tongjiezi Dam cases |
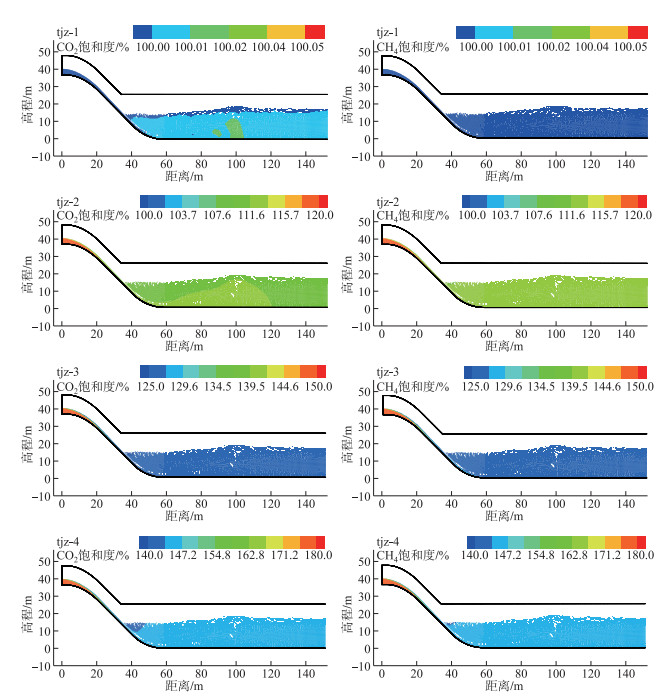
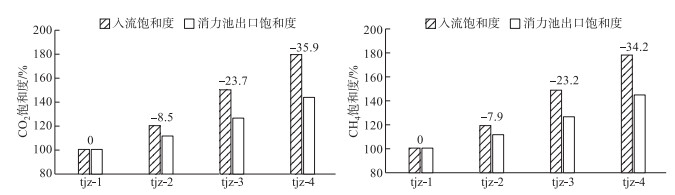
图 5为铜街子电站各计算工况的CO2和CH4的过坝下泄饱和度模拟结果图. 从图中可以看出,当高饱和度的CO2和CH4随水流流经溢流坝面时,受到压强的影响,CO2和CH4的饱和度迅速降低. 当溶解态温室气体随流输移至坝下消力池内时,CO2和CH4的饱和度沿程变化较小. 受到气液传质的影响,温室气体的入流饱和度越高,其在溢流坝面上的释放量也越大. 对消力池出口断面处的CO2和CH4的饱和度进行分析,结果如图 6所示,计算结果表明,当温室气体入流浓度越高,其在坝下的浓度变化值也越大,但受到来流浓度的影响,坝下温室气体浓度也随入流浓度值变高. 从坝面溢流的模拟结果可以看出,由于大气中的温室气体含量比例较低,坝下发生的气液传质程度受到限制,因此上游来流的温室气体浓度大小为影响坝下温室气体浓度分布的主要因素.
|
图 5 铜街子电站各工况温室气体过坝下泄模拟结果 Fig.5 The simulated results of GHG distribution with discharge under different working conditions of Tongjiezi Dam cases |
|
图 6 铜街子电站各工况温室气体消力池出口处饱和度结果(图中数字为饱和度差值) Fig.6 The simulated results of GHG concentration at basin outlet under different working conditions of Tongjiezi Dam cases |
采用大渡河瀑布沟水电站作为典型挑流研究对象,如图 7所示. 电站为堤坝式开发,坝址位于尼日河汇口上游约700 m的大渡河干流,拦河建筑物为直心墙土石坝,最大坝高186 m. 电站装机容量为3300 MW,多年平均年发电量145.8亿kW·h,水库正常蓄水位850 m时,总库容50.64亿m3,水库面积84.14 km2,具有季调节性能. 瀑布沟水电站工程由大渡河主体工程与尼日河引水工程组成,主体工程包括直心墙土石坝、左岸岸边溢洪道、泄水隧洞、放空洞、左岸地下厂房;尼日河引水工程包括泄水闸、进水口、挡水坝和引水隧洞. 其中,左岸溢洪道总长578 m,由进口引渠段、进口溢流堰、泄槽段和出口段组成,采用挑流消能方式. 深孔无压泄水洞布置在左岸地下厂房左侧山体内,采用无压隧洞,出口位于厂房尾水出口下游,采用挑流鼻坎消能.

|
图 7 瀑布沟水电站泄水照片 Fig.7 The picture of Pubugou Dam |
四川大学于2009年对瀑布沟电站的坝下过饱和总溶解气体进行了原型观测,采用原型观测工况,即瀑布沟水电站溢洪道泄水时作为计算工况,对应泄水流量为2570 m3/s,上下游水位差为170.5 m. 本研究设计了4组计算工况,如表 1所示,CO2、CH4的上游来流饱和度范围分别为100 % ~180 %,各工况下的CO2和CH4的初始饱和度均为100 %.
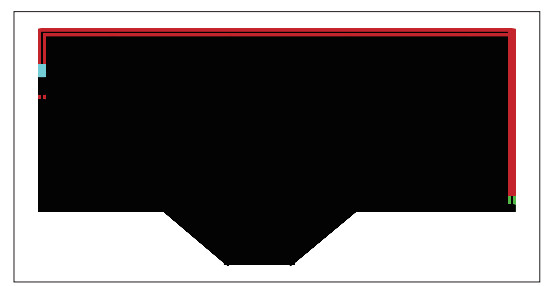
2.2.2 网格划分及边界条件计算区域纵向范围从瀑布沟坝前到坝下约400 m. 计算区域采用2D结构化网格. 鉴于掺气浓度对网格尺寸要求较高,在进行网格划分时,着重对水气交界面及冲坑区域进行加密处理. 该区域网格密度较大,网格尺寸大小仅0.5 m左右,在其他区域纵向和垂向上,网格尺寸大小在0.5~1.5 m之间. 瀑布沟电站计算区域网格划分及边界设置示意图见图 8.
|
图 8 瀑布沟电站计算边界及网格划分示意图 (红色:空气入流;绿色:出流;蓝色:速度入流;黑色:固壁) Fig.8 The boundary condition and mesh of Pubugou Dam cases |
Yang等[14]根据原型观测结果分别对铜街子电站的坝下总溶解气体饱和度分布进行了模型参数率定和验证. 研究结果表明,当气泡粒径均值取0.005 m,模型参数β为1.0时,铜街子电站的坝下总溶解气体饱和度的计算值与实测值的误差在5 % 以内. 模拟结果表明,在此模型参数取值情况下,该模型可以很好地模拟出过坝下泄过程中的气液传质过程和溶解气体浓度分布.
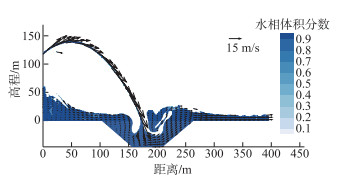
2.2.4 模拟结果分析图 9为瀑布沟电站计算工况泄水时水相体积分数分布及速度矢量图. 水流经溢洪道挑坎末端挑射进入冲坑过程中,挑射水流在空中掺气现象明显,大量空气被卷吸进入水体中. 虽然冲坑底部距离挑坎出口高达160.8 m,挑射水流依然能够进入水体深层,直至冲坑底部,造成水体深层掺气剧烈. 从速度矢量分布可以看出,水流挑射进入冲坑过程中,随着势能转化为动能,水流速度不断增加,冲坑内最大流速高达45 m/s,并在在水舌入水点的上游及下游区域形成漩涡翻滚.
|
图 9 瀑布沟电站自由液面及速度矢量示意图 Fig.9 The free surface and velocity vector of Pubugou Dam cases |
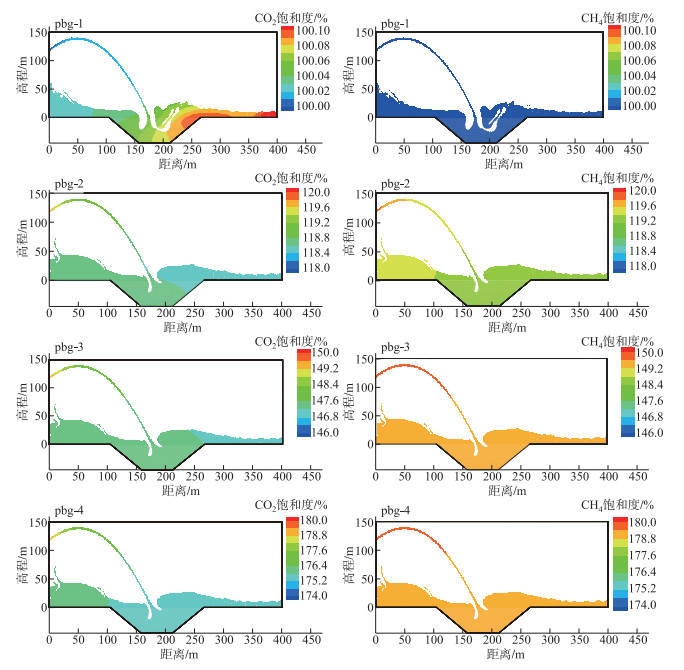
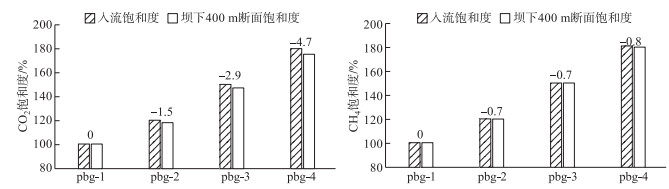
图 10为瀑布沟电站各计算工况的CO2和CH4的过坝下泄饱和度模拟结果图. 从图中可以看出,当高饱和度的CO2和CH4随水流经过空中挑射时,受到压强的影响,CO2和CH4的饱和度出现降低情况. 当溶解态温室气体随流输移至坝下冲坑下游时,CO2和CH4的饱和度沿程变化较小. 对坝下400 m断面处的CO2和CH4的饱和度进行分析,结果如图 11所示. 计算结果表明,当温室气体入流浓度越高,坝下温室气体浓度也越高. 从挑流的模拟结果可以看出,由于大气中的温室气体含量比例较低,坝下发生的气液传质程度受到限制,上游来流的温室气体浓度大小为影响坝下温室气体浓度分布的主要因素.
|
图 10 瀑布沟电站各工况温室气体过坝下泄模拟结果 Fig.10 The simulated results of GHG distribution with discharge under different working conditions of Pubugou Dam cases |
|
图 11 瀑布沟电站各工况温室气体消力池出口处浓度结果(图中数字为饱和度差值) Fig.11 The simulated results of GHG concentration at basin outlet under different working conditions of Pubugou Dam cases |
根据式(17),可知温室气体排放速率由温室气体浓度差及水流流量决定. 分别取进口断面和铜街子电站各计算工况下的消力池出口断面、瀑布沟电站各计算工况下的坝下400 m断面为研究断面计算CO2和CH4的排放速率. 由于目前缺乏对大渡河库区温室气体浓度的监测数据,参考2018年中科院重庆绿色智能技术研究院针对三峡库区温室气体浓度的监测数据,对于铜街子电站,在该泄洪工况下,当上游来流CO2和CH4的浓度分别高达32.1和0.145 mmol/m3时,坝下近坝区的CO2和CH4的排放速率分别可高达4032.3和17.3 mmol/s. 对于瀑布沟电站,在该泄洪工况下,当上游来流CO2和CH4的浓度分别高达32.1和0.145 mmol/m3时,坝下近坝区的CO2和CH4的释放可分别高达2157.0和1.65 mmol/s. 对比可知,对于坝面溢流或空中挑流,当温室气体入流浓度越高,其坝下的温室气体排放速率也越高. 通过前述的分析可知,上游来流的温室气体浓度大小为影响坝下温室气体浓度分布的主要因素,进而影响了坝下温室气体排放速率分布.
然而,对于温室气体过坝下泄排放速率计算模型的研究目前还存在诸多不足. 水流过坝下泄的水动力学模型涉及到高水头、大流速的水气两相流,水动力学的模拟是探究过坝下泄中温室气体浓度及排放速率的基础. 其中,掺气浓度的计算结果直接影响到溶解气体的气泡量进而影响气液传质大小,未来的研究将更一步完善掺气浓度的计算模型,为温室气体浓度的计算提供基础. 此外,已有众多学者对于库区自由液面传质系数进行了研究[18-20],而本研究中采用的库区自由液面传质计算公式,针对高流速下的水流过坝下泄过程,计算结果可能存在误差,未来将进一步完善高流速、强紊动条件下的温室气体自由液面传质系数计算. 在总溶解气体研究中,是将溶解于水体中的气体按照空气组分比例进行分析,而温室气体计算模型中,只考虑单一气体. 因此在模型计算中,在气泡传质源项中采用空气组分比例来表示某种单一温室气体的气泡占比,而可能会与高压条件下实际空气溶解情况不符,为计算带来误差. 未来的工作还将着重考虑在不同泄洪流量、泄流流速等相关水力学因素的影响,并探索可以有效减缓温室气体排放的运行调度措施.
4 结论通过引入过饱和总溶解气体的过坝下泄数值模拟模型,分别考虑CO2和CH4两种温室气体的理化性质,建立了温室气体过坝下排放速率计算模型. 模型基于VOF气液两相流模型,采用RANS紊流模型,分别考虑了溶解气体与水体之间的气泡界面传质与自由液面传质. 通过对典型坝面溢流(铜街子电站)和空中挑流(瀑布沟电站)两种泄流方式下的温室气体浓度分布及坝下排放速率大小的模拟分析,认为由于大气中的温室气体含量比例较低,坝下发生的气液传质量受到限制,因此上游来流的温室气体浓度大小为影响坝下温室气体浓度分布的主要因素,并进而影响坝下温室气体排放速率的大小. 本研究为更进一步准确评估温室气体释放通量提供新的研究思路和技术基础.
| [1] |
Solomon S, Qin D, Mannin M. Historical overview of climate change science. Intergovernmental Panel on Climate Change 2007. Cambridge: Cambridge University Press, 2007: 95-127.
|
| [2] |
Crowley TJ. Causes of climate change over the past 1000 years. Science, 2000, 289(5477): 270-277. DOI:10.1126/science.289.5477.270 |
| [3] |
Tett SFB, Stott PA, Allen MR et al. Causes of twentieth-century temperature change near the Earth's surface. Nature, 1999, 399(6736): 569-572. DOI:10.1038/21164 |
| [4] |
Tremblay A, Lambert M, Demers C. Introduction. Greenhouse gas emissions—Fluxes and processes. Berlin, Heidelberg: Springer, 2005: 21-34. DOI: 10.1007/978-3-540-26643-3_2.
|
| [5] |
Sun ZY, Chen YB, Li C et al. Research of reservoir greenhouse gas emissions in China(2009-2019): Review and outlook. Journal of Hydraulic Engineering, 2020, 51(3): 253-267. [孙志禹, 陈永柏, 李翀等. 中国水库温室气体研究(2009—2019): 回顾与展望. 水利学报, 2020, 51(3): 253-267.] |
| [6] |
Roehm C, Tremblay A. Role of turbines in the carbon dioxide emissions from two boreal reservoirs, Québec, Canada. Journal of Geophysical Research: Atmospheres, 2006, 111(D24): D24102. DOI:10.1029/2006JD007292 |
| [7] |
Abril G, Guérin F, Richard S et al. Carbon dioxide and methane emissions and the carbon budget of a 10-year old tropical reservoir (Petit Saut, French Guiana). Global Biogeochemical Cycles, 2005, 19(4): GB4007. DOI:10.1029/2005GB002457 |
| [8] |
Soumis N, Duchemin É, Canuel R et al. Greenhouse gas emissions from reservoirs of the western United States. Global Biogeochemical Cycles, 2004, 18(3): GB3022. DOI:10.1029/2003GB002197 |
| [9] |
Teodoru CR, Bastien J, Bonneville MC et al. The net carbon footprint of a newly created boreal hydroelectric reservoir. Global Biogeochemical Cycles, 2012, 26(2): GB2016. DOI:10.1029/2011GB004187 |
| [10] |
Chanudet V, Descloux S, Harby A et al. Gross CO2 and CH4 emissions from the Nam Ngum and Nam Leuk sub-tropical reservoirs in Lao PDR. Science of the Total Environment, 2011, 409(24): 5382-5391. DOI:10.1016/j.scitotenv.2011.09.018 |
| [11] |
Huang JP, Lu JY, Li R et al. Numerical study on the cumulative effect of supersaturated TDG through the spillway. Ecohydrology & Hydrobiology, 2021, 21(2): 292-298. DOI:10.1016/j.ecohyd.2021.01.003 |
| [12] |
Wang YS, Politano M, Weber L. Spillway jet regime and total dissolved gas prediction with a multiphase flow model. Journal of Hydraulic Research, 2019, 57(1): 26-38. DOI:10.1080/00221686.2018.1428231 |
| [13] |
Cheng XJ, Chen YC, Chen XW. Numerical simulation of dissolved oxygen concentration in the downstream of Three Georges Dam. Journal of Hydrodynamics: Ser A, 2009, 24(6): 761-767. [程香菊, 陈永灿, 陈雪巍. 三峡工程坝身泄流下游水体溶解氧浓度数值模拟. 水动力学研究与进展: A辑, 2009, 24(6): 761-767.] |
| [14] |
Yang HX, Li R, Liang RF et al. A parameter analysis of a two-phase flow model for supersaturated total dissolved gas downstream spillways. Journal of Hydrodynamics: Ser B, 2016, 28(4): 648-657. DOI:10.1016/S1001-6058(16)60669-8 |
| [15] |
Cheng XJ, Xie J, Yu DG et al. Calculated analysis of oxygen transfer from air bubble-water interface and turbulent water surface in microporous aeration systems. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(13): 190-199. [程香菊, 谢骏, 余德光等. 曝气增氧微气泡-水界面和水体表面的氧传质的计算分析. 农业工程学报, 2013, 29(13): 190-199.] |
| [16] |
Cheng XJ, Xie YN, Zhu DT et al. Modeling re-oxygenation performance of fine-bubble-diffusing aeration system in aquaculture ponds. Aquaculture International, 2019, 27(5): 1353-1368. DOI:10.1007/s10499-019-00390-6 |
| [17] |
Jähne B, Libner P, Fischer R et al. Investigating the transfer processes across the free aqueous viscous boundary layer by the controlled flux method. Tellus B, 1989, 41B(2): 177-195. DOI:10.1111/j.1600-0889.1989.tb00135.x |
| [18] |
Cole JJ, Caraco NF. Atmospheric exchange of carbon dioxide in a low-wind oligotrophic lake measured by the addition of SF6. Limnology and Oceanography, 1998, 43(4): 647-656. DOI:10.4319/lo.1998.43.4.0647 |
| [19] |
MacIntyre S, Wanninkof R, Chanton JP. Trace gas exchange across the air-water interface in freshwater and coastal marine environments// Matson PA, Harriss RC eds. Biogenic trace gases: Measuring emissions from soil and water. New York: Blackwell Science, 1995: 52-97.
|
| [20] |
Crusius J, Wanninkhof R. Gas transfer velocities measured at low wind speed over a lake. Limnology and Oceanography, 2003, 48(3): 1010-1017. DOI:10.4319/lo.2003.48.3.1010 |
 2022, Vol. 34
2022, Vol. 34 

