(2: 河海大学水文水资源学院,南京 210098)
(3: 河海大学土木与交通学院,南京 210098)
(2: College of Hydrology and Water Resources, Hohai University, Nanjing 210098, P.R.China)
(3: College of Civil and Transportation Engineering, Hohai University, Nanjing 210098, P.R.China)
太湖流域位于长江三角洲南缘,人口稠密、城市集中、经济发达. 太湖也是承载长三角地区社会经济发展的重要水源地,在长三角一体化的发展趋势下太湖的地位更加重要. 2005年起进入长效运行的“引江济太”望虞河工程在抑制、改善贡湖出现水华方面发挥了重要作用[1],在提升流域水资源和水环境承载能力方面形成重要支撑[2]. 发展改革委规划的《太湖流域水环境综合治理方案》中,“新孟河延拓疏浚”作为重点的工程项目,将长江水直接引入太湖的竺山湖区,协同已有的望虞河引排通道,太湖将形成“二引三排”的新格局[3]. 2007年以来,太湖经过大力度综合性治理,截止2015年水中总氮(TN)和总磷(TP)浓度稳定下降[4]. 但是2016年的特大洪水携带流域大量的污染物入湖[5],太湖全湖TP出现反弹[6],太湖磷成为一个重要的控制因素. “新孟河延拓疏浚”完成后的格局下,“新孟河引水”对太湖水环境尤其是总磷会有怎样的影响?如何使“新孟河引水”兴利避害,事半功倍的完成太湖流域“两个确保”的任务?这是一个值得研究的问题.
磷作为湖泊富营养化的重要指标以及蓝藻生长的必要元素,进入湖泊后,在太湖的磷循环系统中,除经出湖河流流出和生物利用后被捕捞带出[7],会持续的在底泥-湖水-生物体间迁移转化[8]. 对于太湖磷循环系统的研究表明[4],太湖水中TP存在明显“西浊东清”的结构,西北湖区(竺山湾、梅梁湾、西部沿岸区)水体TP在0.15 mg/L左右,水中磷存量约338 t,占全湖的50 %;东南湖区(东太湖、东部沿岸区、南部沿岸区)水体TP在0.05 mg/L左右,水中磷存量约67 t,只有西北湖区1/5. 有研究指出近几年东太湖水质有恶化的趋势,TP有上升的苗头[9]. “新孟河引水”从西北部入湖,如果从东南部出湖,入湖水量增加虽然能够改善西北部湖区的水质及富营养化状况,但可能会改变原有“西浊东清”水质结构,均化的东西水质可能造成东太湖水中TP浓度的上升. 同时,加大入湖水量在一定程度上会缩短太湖的交换周期,有改善西北部水质、抑制水华的效果[10],但同时对入湖通量以及水质结构也会有不利影响[11]. 如能通过出水路线的合理规划使得西北部TP偏高的湖水不经东南出湖,形成西北小循环,对太湖总磷的削减可能会有更好的影响.
通过水利工程的合理调度,形成良好水循环,改善湖泊水质,这是国内外富营养化湖泊治理的手段之一. 塔玛特湖[12]、滇池[13]、巢湖[14]都取得了一定的改善效果. 一般而言,对于引水工程效果的评价,必须有水质指标的连续监测数据[15],这是一项耗时费力,成本极大的监测项目. 因此除实地监测外,数值模拟也是估算湖泊水质的重要手段. Li等基于EFDC模型研究了长江通过望虞河向太湖引水以增强水动力、缓解太湖富营养化态势的过程中,不同引水方案对二者的影响,结果表明,太湖各湖区对不同调水路线响应不同[16]. Yan等基于BHF模型预测了滇池在不同治理措施下总磷和藻类生物量的变化,结果表明,滇池大量外源磷的输入使得湖内大量磷沉积,控制外源输入刻不容缓[17]. Elshemy等基于MIKE 21模型预测了未来沿湖城市排放污水对埃及满扎拉湖水环境的影响,结果表明,快速城市化造成的污染物通量及入湖水量增加会急剧恶化满扎拉湖的水环境[18]. 这些研究都能从一定范围内评价引水工程对湖泊水质的影响,使用水文-水质模型可以在引水前合理的预测引水对湖泊水环境的影响,因此使用水文-水质模型是对引水工程效果进行评价的方法之一.
针对“新孟河引水”工程,如何设计出水路线才能趋利避弊,使西北部水质改善最明显,东南部水质维持良好的现状?本研究开展工作将推进涉及湖泊出水的优化研究,为太湖“两个确保”任务提供有力保障,在应用中为管理部门形成切实可行的方案提供技术支撑. 同时在新的状态下,太湖各湖区尤其是东太湖的总磷怎样变化?太湖年内的总磷变化是怎样的?磷的收支平衡是怎样的?都是值得讨论的科学问题. 这些问题的初步研究有助于在流域尺度上反演、预测太湖磷的变化过程,为评估近年来太湖磷反弹及今后各类治理措施对太湖磷浓度的影响有着指导作用,有助于提出针对太湖磷控制的管理运行和治理措施上的明确建议.
本文以近些年太湖的水文水质数据为基础,模拟了不同路线对太湖分湖区总磷的影响,力求将“新孟河引水”对太湖的影响进行一个清晰的分析,并支撑形成更合理的出水路线.
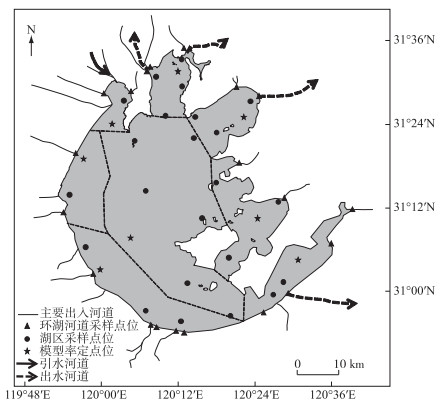
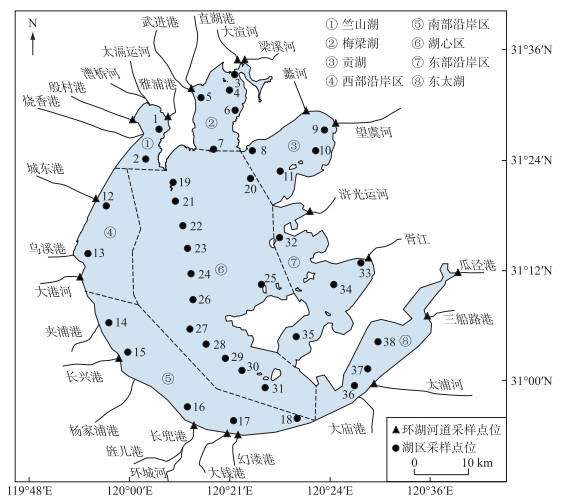
1 材料与方法 1.1 研究区域太湖流域面积36895 km2,其中太湖湖区面积3192 km2(包括部分湖滨陆地)[3],太湖湖区库容约为50亿m3,平均水深1.9 m. 流域内水面总面积约5551 km2,出入太湖河流228条,其中主要入湖河流有22条. 太湖流域属亚热带季风气候区,降水丰沛,四季分明,夏季炎热. 年平均气温14.9~16.2℃,多年平均降水量1177 mm. 太湖的湖区分区及采样点设置见图 1,按照泰森多边形法对湖区进行划分,设置了31个湖内采样点位,在出入湖主要河道设置了22个采样点位.
|
图 1 太湖湖区分区及采样点设置 Fig.1 Division of Lake Taihu and its sampling sites |
(1) 收集数据
逐月各段面太湖出入湖水量、磷通量、逐日水位变化数据收集自太湖流域水资源保护局,各段面太湖出入湖磷浓度的数据是根据水量和通量的关系计算得到. 2007-2020年太湖流域逐日降雨量、蒸发量、水温、逐小时风速、风向数据收集自中国气象科学数据共享平台无锡站(http://data.cma.cn).
(2) 自测数据
本研究于2020年10月在环太湖23条主要出入湖河流出入湖河口及湖内48个监测点位进行了采样,检测了总磷(TP)浓度、溶解性总磷(DTP)浓度、颗粒态总磷(PP)浓度、溶解氧(DO)、氧化还原电位(ORP)、叶绿素a(Chl.a)浓度等指标. 太湖各段面出入湖总磷通量中溶解性总磷和颗粒态总磷的占比来自这次采样的结果. 自测数据的采集、整理方法详见附录第1节.
1.2.2 平均年设置本研究基于2010-2017年(2016年为特大洪水年除外)逐月各段面太湖出入湖水量和磷通量数据设置了一个平均年,平均年的太湖降雨量、蒸发量、风速、风向均采用2007-2020年的平均值,平均年太湖各出入湖河道逐月的总磷浓度根据该月的出入湖水量与磷通量计算得到. 平均年数据的模拟计算可以代表太湖的多年平均状态. 为反映引水对太湖总磷的一般性影响,以多年平均状态做为基准,太湖各出入湖河道正常出入湖,在此基础上增加新孟河引水.
1.2.3 不同出水路线的情景设置根据太湖现在的出入河格局、已建工程的条件,设置了以望虞河、新孟河作为引水通道,利用现有工程或进行一定的工程改造后梁溪河、新沟河、走马塘、太浦河作为可能的出水通道进行设定,本研究模拟的出水路线见表 1.
| 表 1 模拟出水路线 Tab. 1 Setting of outlet paths |
新孟河设计引水量为20亿m3/a[3],但是在未来使用中考虑到防汛抗旱、生态应急调度的共同控制,实际引水量未必会达到设计引水量. 本研究为清晰地反映“新孟河引水”对太湖总磷的影响,模拟中设置引水量为设计的20亿m3/a,其中1-5月之间引入14亿m3,日引水流量为108 m3/s,11-12月再引入6亿m3,日引水流量为115.7 m3/s. 入湖TP浓度设置为与2010-2017年望虞河入湖TP浓度的平均值一致. 模拟中设置新孟河引水过程参考了2011年“引江济太”望虞河引水入湖过程[19],因为该年太湖入湖水量109亿m3,其中包含望虞河引水量17亿m3,入湖水量与引水量与模拟设置的平均年接近. 设置的出水河道出湖TP浓度与该湖区其他出湖河道逐月的TP浓度均值保持一致,逐月出水河道水量为原有出水量与引水增加的出水量之和,引水及出水通道位置见图 1.
1.3 太湖总磷模型 1.3.1 模型建立(1) 水动力子模型
本研究建立的平面二维水动力子模型包括太湖湖面及环湖主要出入湖河道(图 1),面积2338 km2,建模区域太湖底部高程数据来自太湖流域水资源保护局. 经纬度坐标系选取WGS84坐标系,投影带坐标系选取北京1954坐标系,中央经线为120°E. 本研究将建模区域划分为19885个三角形网格,未进行局部加密,网格大小范围为0.08~0.14 km2,环湖主要出入湖河流河口设置为可自由出入节点. 水动力子模型为模拟太湖总磷变化提供了水动力背景. 水动力子模型详见附录第2节.
(2) 磷循环子模型
本研究建立的磷循环子模型在模拟磷浓度的变化时,除了基于水动力子模型计算磷随流场的迁移扩散外,还综合考虑了以下过程:①磷通量出湖与入湖;②湖内颗粒态磷的沉降与悬浮(公式(1));③湖内底泥对溶解态总磷的吸附与释放(公式(2));④湖内藻类生长与死亡对颗粒态磷及溶解态磷的影响(公式(3));⑤藻类打捞及水生植物收割对颗粒态磷及溶解态磷的影响(公式(2));⑥浮游动物生长与死亡对颗粒态磷及溶解态磷的影响(公式(3)~(4)).
| dDPdt=−sev+rsev+0.1UMP | (1) |
| dDTPdt=−UPP+0.9UMP+Pre−Pad | (2) |
| UPP=upp(P−θ(T−20)1)F(N,P) | (3) |
| UMP=umpKθ(T−20)1TPTP+HS_TPPmaxPmax+HS_Pmax | (4) |
式中, DP为无机颗粒磷浓度;sev和rsev是无机颗粒磷沉降和再悬浮系数;Pre是底泥释放系数;Pad是溶解性总磷损失系数(包括底泥吸附和渔获、水草收割、藻打捞的损失);UPP是藻摄取磷的系数;upp是藻摄取磷的速度;UMP是微生物控制藻生物量的系数;ump是微生物分解藻的速度;F(N, P)为藻光合作用的营养盐限制函数;K是描述摄入速率依赖浮游植物生物量因素;θ1是植物光合作用和呼吸作用与温度相关的阿伦尼斯温度系数;T是水温;HS_TP为微生物摄取磷的半饱和浓度;HS_Pmax为有机物降解的半饱和由植物泌氧产生的DO浓度;Pmax是植物午时最大产氧量.
Eutrophication model核心控制方程如下:
| ∂PTP∂τ+ux∂PTP∂x+uy∂PTP∂y+uz∂PTP∂z=DTP(∂2PTP∂x2+∂2PTP∂y2+∂2PTP∂z2)+RTP | (5) |
| RTP=n∑i=1rTPi | (6) |
式中,rTP为过程①~⑥的计算,计算公式见公式(1)~(6).
1.3.2 边界条件及初始条件(1) 初始条件
本研究模拟“新孟河引水”对太湖总磷的影响是采用考虑前一年湖泊水质-动力学过程的方式,预先按照平均年的水文、水质条件进行计算了一年,作为模拟开始时的初始条件. 在进行不同出水路线的效果对比时,除直接参与引出水的河道水量、水质根据模拟情况设置外,环湖其余出入湖河道水量、水质均与平均年一致. 引出水过程及其后的水动力、水质计算持续按照平均年的水文、气象状态按照1年的时间尺度连续进行.
(2) 边界条件
本研究使用2016年逐月各段面太湖出入湖水量、磷通量数据及无锡站逐小时风速、风向数据进行模型建立与率定. 建立好的模型使用平均年数据模拟太湖的一般状态,在此基础上设置新孟河引水的不同出水路线(附录2.4).
1.3.3 模型率定与验证(1) 主要参数
本研究参照之前浅水湖泊水质模拟的参数设定[20],使用2016年太湖流域的水文-水质数据反复试算,最终确定水动力-磷循环模型中关键参数的取值,见表 2. 磷循环子模型的敏感参数是无机颗粒磷沉降系数.
| 表 2 水动力-磷循环模型关键参数 Tab. 2 Key parameters of the hydrodynamic- phosphorus cycle model |
(2) 率定与验证
本研究通过比较2016年太湖内实测与模拟水位来率定水动力子模型精度,通过比较2016年太湖实测与模拟的湖内测点的TP浓度来率定磷循环子模型精度,将模型精度的指标列于表 3,测点位置见图 1.
| 表 3 模型精度 Tab. 3 Model calibration |
太湖内实测与模拟水位的均方根误差为0.11 m,纳什系数为0.91,因此本研究建立的水动力子模型对太湖出入湖流量的模拟是准确的. 在太湖各湖区的中心选取一个测点,从各湖区测点的TP浓度来看,均方根误差和纳什系数均符合要求,本研究建立的磷循环子模型对太湖内磷变化过程的模拟是基本准确的(表 3). 2016年各测点逐月实测TP浓度与模拟值比较详见附录2.5.1.
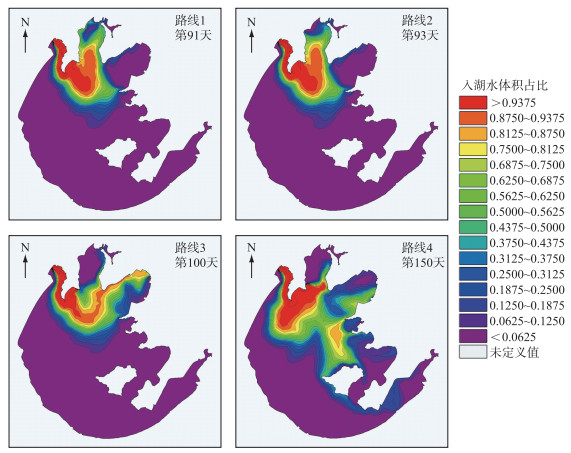
2 结果 2.1 不同出水路线下新孟河引水的迁移途径将新孟河开始引水后,引水入湖最早到达各路线设计的出湖河道之日,自入湖至出湖的迁移轨迹绘制在图 2,将不同出水路线下1月1日开始的新孟河引水首次到达各湖区边界的时间记录在表 4. 由表 4可见,除受水湖区竺山湖外,所有路线的新孟河引水入湖后在15 d内即可抵达湖心区北部边界,35 d内即可到达湖心区中心. 若出水河道设置在走马塘(路线3),新孟河引水入湖抵达贡湖的时间会从100 d左右下降至63 d. 若出水河道设置在太浦河(路线4),新孟河引水入湖抵达梅梁湖的时间会从60 d左右上升至101 d,且只要125 d即可抵达东太湖,远小于近十年太湖约184 d的交换周期[11].
|
图 2 新孟河引水入湖迁移路线 Fig.2 Migration route of water from Xinmeng River |
| 表 4 新孟河引水入湖抵达各湖区时间(d)* Tab. 4 Time of arrival of water from Xinmeng River |
由图 2可见,若出水河道设置在梅梁湖东西两侧的新沟河、梁溪河(路线1~2),新孟河引水后水流主要经过竺山湖和梅梁湖,对其它湖区的影响不大. 若出水河道设置在贡湖的走马塘(路线3),水流主要经过竺山湖和贡湖,对梅梁湖内湾以及其它湖区的影响较小. 而出水河道设置在东太湖的太浦河(路线4)引水可流经竺山湖以及西部湖区,对梅梁湖、贡湖的影响较小,这一路线的水流一直会流经湖心区进入东太湖. 由于在模拟新孟河引水时,环湖其余河道仍在正常出入湖,太浦闸是最大的出湖河道(占比34 %),而城东港是最大的入湖段面(占比42 %),因此路线4中,自城东港入湖的主流将新孟河引水推移的更接近西山岛和东部沿岸区.
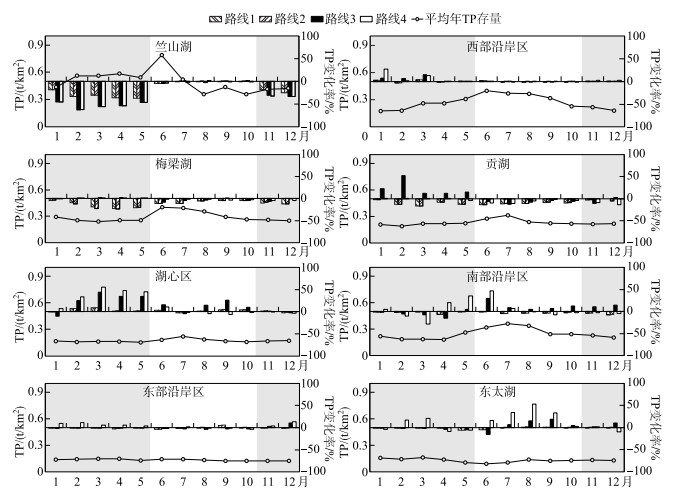
2.2 不同出水路线对太湖各湖区总磷的影响为反映不同湖区水中磷存量对不同出水路线的响应,将各引水工况下太湖各湖区逐月单位面积水中总磷存量与不引水工况之间的变化绘制为图 3. 此外,根据2.1的结果分析,在受引水影响大的湖区选择了6个典型监测点,将不同路线下这些监测点的月均总磷浓度变化绘制于图 4,分析湖内典型测点总磷浓度对不同出水路线的响应. 考虑到11-12月的新孟河引水对太湖东南部的影响主要在下一年才会出现,因此主要分析1-5月的引水影响.
|
图 3 太湖各湖区单位面积磷存量变化(灰色背景为引水期) Fig.3 Changes of phosphorus stock per unit area in each district of Lake Taihu (The gray background is the diversion period) |
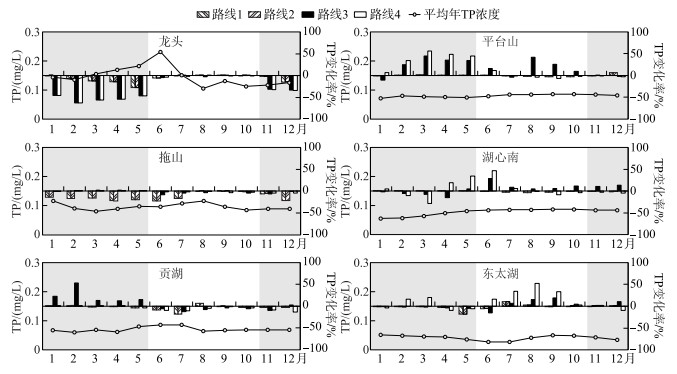
|
图 4 太湖典型监测点总磷浓度变化(灰色背景为引水期) Fig.4 Changes of TP at monitoring sites in Lake Taihu (The gray background is the diversion period) |
由图 3可见,引水可显著降低竺山湖的TP,相比平均年,4种出水路线竺山湖的逐月TP在引水期的降低范围是18 % ~63 %,平均值38 %. 出水河道设置在梅梁湖时(路线1~2),引水对梅梁湖TP的降低也是有利的,2种出水路线梅梁湖的逐月TP在引水期的降低范围是3 % ~23 %,平均值14 %. 对贡湖而言,出水河道设置在梅梁湖时(路线1~2),引水对贡湖TP的降低是有利的,平均降低了8 %. 但是当出水河道设置在走马塘(贡湖)时(路线3),引水期贡湖的TP会上升,平均值为15 %,引水结束后贡湖的TP才会下降. 引水会显著增加湖心区的TP,4种出水路线湖心区的逐月TP在引水期平均增加了13 %. 当出水河道设置在太浦河时(路线4),东太湖和南部沿岸区的TP都显著上升,从全年来看,东太湖最大增幅达到52 %,南部沿岸区最大增幅达到46 %. 西部沿岸区和东部沿岸区TP受引水影响不大.
由图 4可见,引水期龙头(竺山湖)测点的TP浓度下降明显,平均年1-5月龙头的TP浓度平均值为0.16 mg/L,引水后的TP浓度下降范围为0.02~0.08 mg/L. 出水河道设置在梅梁湖时(路线1~2),拖山(梅梁湖)的TP浓度也会下降,引水期的平均TP浓度会从平均年的0.095 mg/L下降到0.072 mg/L. 出水河道设置在走马塘(路线3),贡湖(贡湖)和平台山(湖心区中部)的TP浓度会上升. 而出水河道设置在太浦闸(路线4),湖心南(湖心区东南部)和东太湖(东太湖)的TP浓度会上升,由于引水在湖内迁移的时间,湖心南TP浓度开始上升的时间在5月,从平均年的0.075 mg/L增加到0.110 mg/L,东太湖TP浓度开始上升的时间在8月,从平均年的0.041 mg/L增加到0.063 mg/L.
综上,无论是对各湖区水中磷存量还是典型测点的总磷浓度分析,均发现引水对于太湖西北部改善效果明显,但是若出水设置在东太湖,则对太湖东南部有不利的影响.
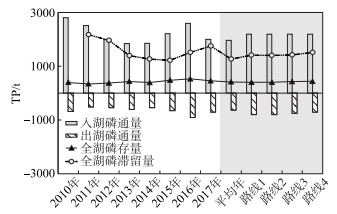
2.3 引出水对太湖磷循环的影响 2.3.1 实测数据得到的太湖磷平衡结果由图 5可见,2010年以来太湖年入湖磷通量平均2224 t/a,年出湖磷通量平均648 t/a,差值为1576 t/a. 而太湖水中磷存量大致稳定,为420 t±100 t,根据物料平衡计算,入湖总磷在湖中年滞留量平均值为1608 t. 本研究模拟的平均年入湖磷通量1958 t,出湖磷通量638 t,差值为1320 t,太湖水中磷存量约为409 t,磷滞留量为1265 t. 而模拟的新孟河引水后年入湖磷通量2186 t,比平均年多带入磷通量228 t,根据出水河道不同,出湖磷通量为712~802 t,出水河道设置在梅梁湖出湖磷通量最高,太湖水中磷存量为398~434 t,磷滞留量为1403~1514 t,出水河道设置在东太湖的磷滞留量最高.
|
图 5 太湖磷收支变化(灰色背景为模拟结果) Fig.5 Budget changes of phosphorus in Lake Taihu (The gray background is the simulation result) |
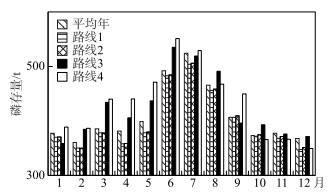
由图 6可见,本研究模拟的太湖逐月水中磷存量的变化范围在360~524 t之间,平均409 t. 路线1和路线2的月均水中磷存量分别为397和399 t,小于引水前的平均值. 而路线3的月均水中磷存量是425 t,路线4的月均水中磷存量是434 t,稍大于引水前的平均值. 从这些结果来看,出水河道设置在梅梁湖,会降低全湖水中磷存量,反之则会增加太湖水中磷存量.
|
图 6 出水路线与太湖水中磷存量的关系 Fig.6 Relationship between outlet paths and phosphorus storage in Lake Taihu |
“新孟河引水”的不同出水路线对太湖总磷会产生怎样的影响?哪一条出水路线是最优的调度方案?从太湖水中TP存量的对比看,相比平均年,路线1~2降低了太湖水中TP存量,而路线3~4显著增加了太湖水中TP存量. 从太湖各湖区单位面积水中磷存量的对比来看,不同出水路线对降低竺山湖TP的效果是一致的,虽然不同出水路线都会增加湖心区的TP,但是出水河道设置的离新孟河入湖口越远,湖心区的TP上升越明显. 只有出水河道设置在贡湖的望虞河-走马塘,贡湖的TP才会显著上升. 而出水河道设置在东太湖的太浦闸,会造成东太湖、南部沿岸区TP明显的上升. 从全湖水中TP存量和各湖区单位面积水中磷存量的对比来看,出水河道设置在梅梁湖的梁溪河(路线1)和新沟河(路线2),形成太湖西北部小循环是最优的出水路线. 但是西北部出湖河道目前存在出水能力不足的缺点,这在未来应用中是一个不可忽略的工程问题.
本文从科学研究的角度,对“新孟河引水”后各单一出水路线的结果进行了比较,在未来应用中,管理部门显然可以在引水后组合不同的出水路线,如根据梅梁湖和贡湖的TP浓度实时变化进行出水路线的轮换,达到更好的引清排浑的效果,形成出水的联动方案,限于掌握的太湖实际调度资料有限,本文就不在这一方面进行更深入的探讨.
3.2 太湖各湖区总磷对不同出水路线的响应为什么太湖不同湖区的总磷对不同出水路线的响应不同?从图 2和表 4的新孟河引水迁移路线和时间来看,形成太湖西北部小循环时(路线1~2),总磷偏高的竺山湖水和引进的新孟河水会直接经过湖心区北部和梅梁湖出湖,对水质较好的贡湖、南部沿岸区、东太湖不会造成太大影响. 而出水河道设置在望虞河-走马塘(路线3)和太浦闸(路线4)时,太湖西北部总磷偏高的湖水会对水质较好的湖区造成不利的影响. 从贡湖和东太湖TP上升的时间来看,与新孟河引水抵达该湖区的时间是相近的,因此贡湖和东太湖TP上升存在滞后性. 新孟河引水虽未直接经过南部沿岸区,但是水体交换造成总磷偏高的竺山湖和西部沿岸区的湖水进入南部沿岸区,恶化了该区域的TP.
从全湖水中磷存量的对比来看,路线1~2的全湖月均水中磷存量比路线3少27 t,比路线4少了36 t. 本研究模拟的新孟河引水增加太湖磷通量228 t,即外源磷输入的增量是一致的. 但是由于梅梁湖的TP浓度大于贡湖大于东太湖[6],因此出水河道设置在梅梁湖带出的磷通量会更多. 以近十年这3个湖区平均TP浓度计算,出水河道设置在梅梁湖可带出磷通量164 t,比出水河道设置在贡湖(路线3)多46 t,比出水河道设置在东太湖(路线4)多90 t. 湖泊对于入湖的总磷也有转化的能力,入湖水在太湖中时间越长,转化效果越好[11]. 从这个角度来看,路线3和路线4入湖的新孟河水在太湖中停留的时间更长,因此太湖对总磷的去除量更大,所以路线3~4全湖水中总磷存量相比西北小循环的增加量是小于出入湖磷通量的差值的. 但是路线4的调度安排下,新孟河引水125 d左右即可到达东太湖,远小于近10年太湖约184 d的交换周期,之前的研究[11]表明,交换周期的减少已经对太湖水质的空间格局及东太湖造成不利的影响,因此路线4中新孟河引水对东太湖的影响是值得重视的问题.
考虑到季风作用,路线4中,7-9月东太湖总磷浓度虽然上升,但是藻受风生流的输运会远离东南部水源,这在一定程度上减轻了引水对东南部水源区的影响. 从这个角度来看,在太湖这样风生流影响强烈的大型浅水湖泊中,未来三维模型在模拟太湖总磷的变化时会有更好的表现. 本次研究的核心是立足于多年、长序列太湖磷过程的数据,建立一个简化的太湖磷出入/归趋模型,从节约算力的角度,太湖流场模拟选择了二维的水动力子模型,在模拟太湖风生流过程是会存在一些不足,这是后续研究值得改进的地方.
3.3 太湖磷平衡分析太湖年内的磷平衡是怎样的?从物料平衡的角度看,太湖输入磷通量多,输出磷通量少,近年来水中磷存量大致稳定,每年平均有1608 t磷滞留,有研究[21]表明,通过水草收割、渔获、蓝藻打捞等途径离开太湖的磷年均约230 t. 因此,通过沉降和底泥吸附滞留在太湖底泥中的磷约有1300 t/a. 未引水平均年的状态和考虑引水后磷的平衡状态没有变化,底泥都表现为磷汇,平均年的磷滞留量为1265 t,引水后4种出水路线年均滞留量为1435 t,其中出水河道设置在东太湖(路线4)磷滞留量最大,年滞留1513 t;出水河道设置在梅梁湖(路线1~2)磷滞留量1404 t左右;出水河道设置在望虞河-走马塘(路线3)磷滞留量为1417 t. 磷滞留量可以作为评价太湖水环境的重要指标,就目前的结果而言,如果入湖总磷没有明显下降,磷滞留量仍会维持在高位.
4 结论1) 新孟河引水后不同的出湖途径对太湖产生的效果存在差异,不同湖区的响应也有所不同. 对于竺山湖而言不管哪条路线都有明显的改善效果;对于贡湖而言从望虞河-走马塘出水时TP会有所上升;对于湖心区而言出水河道设置的离新孟河入湖口越远,其TP上升的越明显;对于太湖东南部而言如果从太浦河出水其TP的上升比较显著. 因此,选择出水路线应该进行综合考虑.
2) 从单一出水路线的角度来看,新孟河引水,梁溪河或新沟河出水的西北小循环是“新孟河引水”工程的优化出水路线,在降低竺山湖、梅梁湖总磷的同时,不对太湖东南部水质产生不利影响,对太湖总磷也有降低的效果. 在应用中可以根据实际情况组合不同的出水路线,形成联动方案,使“新孟河引水”发挥更大的作用.
3) 从物料平衡的角度看,太湖底泥目前仍是磷汇. 引水后4种出水路线年均滞留量为1435 t,其中出水河道设置在东太湖(太浦闸)磷滞留量最大,年滞留1513 t,出水河道设置在梅梁湖(新沟河、梁溪河)磷滞留量最小,年滞留1404 t左右.
5 附录附录见电子版(DOI: 10.18307/2022.0411).
附录 1 自测数据全湖区及环湖河道采样时间为2020年10月14 18日,采样范围为太湖8个湖区以及环湖共18条河道,具体采样点位详见附图Ⅰ. 湖内共设置38个采样点,环湖河道共设置18个采样点,所有点位均采集水样. 其中,湖内12、21、23、26~27、29~31、36~37号点位除采集水样外,还采集了表层5 cm底泥.
|
附图Ⅰ 太湖湖区及环湖河道采样点位 AttachedFig1 Districts of Lake Taihu and sampling sites around the lake |
所有点位水样采用5 L有机玻璃采水器分上、中、下3层共采集15 L于水桶中混合均匀,并倒出约250 mL左右水样用于测定总磷浓度(TP)、溶解性总磷浓度(DTP)、颗粒态总磷浓度(PP)、溶解氧(DO)、氧化还原电位(ORP)和叶绿素a浓度(Chl.a). 表层底泥采用活塞式有机玻璃柱柱状采泥器采集,缓慢倒掉上覆水后用塞子将柱子上下口临时封好,用胶带加固后放入架子内带上岸,再利用切片切取表层5 cm底泥封存.
2 太湖总磷模型的建立 2.1 概述太湖流域水文、环境过程极其复杂,既要考虑不同段面携带的污染物在湖里的迁移扩散,又要考虑风生流对大型浅水湖泊流场的影响. 此外,湖中生物磷的理化反应也会造成总磷的变化. 因此,要建立一套能够反应太湖完整水资源、磷循环过程的系统模拟模型,需要耦合水动力模型和水质模型,目前MIKE模型软件系统已经覆盖了水环境领域的各个方向,具有整合计算优势. MIKE 21 HD模块是非常通用的水文学工具,它可以用来描述各种水力现象,为污染物迁移扩散提供了水动力学计算基础. ECOLab模块是一个完备的、用于生态模拟的水质模块,该模块用于河流、湿地、湖泊、水库等的水质模拟,预报生态系统的响应、简单到复杂的水质研究工作、水环境影响评价及水环境修复研究、水环境规划和许可研究、水质预报等方向.
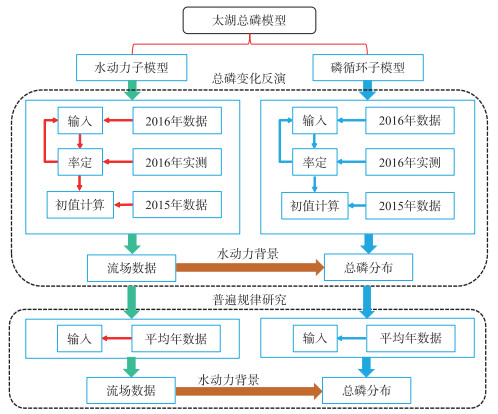
太湖水文条件复杂,MIKE模型兼具水动力模块和水质模块,可以整合太湖水动力背景模拟与水质模拟,是最适合的水文水质模型. 太湖流域总磷模型构建的思路见附图Ⅱ.
|
附图Ⅱ 太湖总磷模型构建流程图 AttachedFig2 Flow chart of model construction |
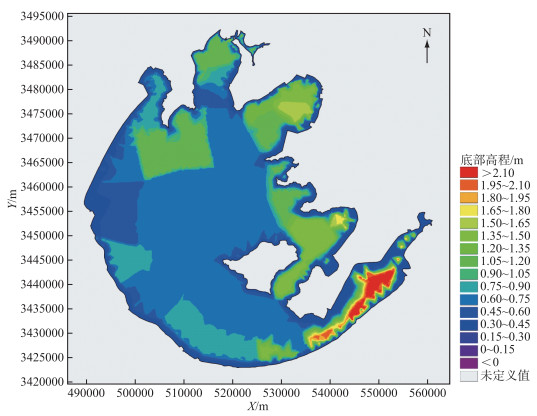
本研究模拟范围为太湖流域湖面部分,面积2338 km2. 经纬度坐标系选取WGS84坐标系,投影带坐标系选取北京1954坐标系,中央经线120°E. 湖底高程数据(附图Ⅲ)由太湖流域管理局提供的湖内33个测点的水量、水位数据反算并插值得到.
|
附图Ⅲ 太湖底部高程图 AttachedFig3 Elevation map of Lake Taihu |
由于模型中的区域是处在干湿边交替区,为了避免模型计算出现不稳定性,本次模拟启动了Flood and Dry的选项. 在这个情形下本次模拟设定一个干水深(drying depth)、淹没深度(flooding water depth)和湿水深(wetting depth). 当某一单元的水深小于湿水深时,在此单元上的水流计算会被相应调整,而当水深小于干深度的时候,会被冻结而不参与计算. 淹没深度是用来检测网格单元是不是已经被淹没. 当水深小于湿水深的单元会做相应调整,即不计算动量方程,仅计算连续方程.
2.2.3 涡粘系数流体所引起的雷诺附加应力,其空间尺度远小于网格尺度,为解决此问题引入了涡粘概念,来描述这种作用于流体质点在时间上积分. 将变量拆解为平均流及紊流扰动,生成了其它附加的剪力项,包含在动量方程式中层流剪力和紊流的雷诺剪力. 增加涡粘系数,可以将变量拆解为平均值的情形加以梯度化,减低多余剪力所造成的影响. 本研究涡粘系数根据Lilly(1967)、Leonard(1974)、Aupoix(1984)、Horiuti(1987)选取为0.5.
2.2.4 时间步长经过多次比选,既满足计算精度又满足计算时间要求的时间步长为10 min,模拟计算时间为365 d.
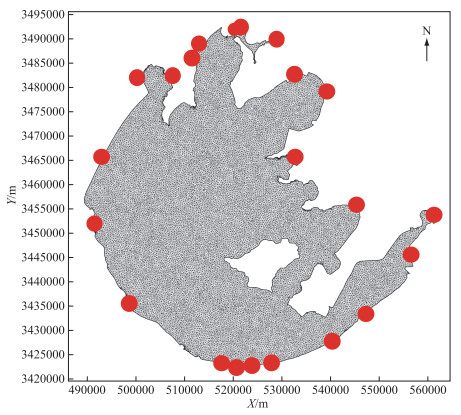
2.2.5 网格划分本研究用三角形网格将太湖水面部分均匀划分成19885个网格,出入湖河道设置成点源输入输出(附图Ⅳ).
|
附图Ⅳ 太湖网格划分图 AttachedFig4 Grid division map of Lake Taihu |
太湖流域水平尺度远大于垂直尺度,由于水深、流速等水力参数沿垂直方向的变化比沿水平方向的变化要小的多,因此,将三维流动的控制方程沿水深积分,并取水深平均,可得到沿水深平均的二维浅水流动质量和动量守恒控制方程组. 其连续性方程、X和Y方向动量方程,分别为:
| \frac{{\partial h}}{{\partial t}} + \frac{{\partial h\bar u}}{{\partial x}} + \frac{{\partial h\bar v}}{{\partial y}} = hS | (1) |
| \begin{array}{l} \frac{{\partial h\bar u}}{{\partial t}} + \frac{{\partial h{{\bar u}^2}}}{{\partial x}} + \frac{{\partial h\overline {uv} }}{{\partial y}} = f\bar vh - gh\frac{{\partial \eta }}{{\partial x}} - \frac{h}{{{\rho _0}}}\frac{{\partial {p_a}}}{{\partial x}} - \frac{{g{h^2}}}{{2{\rho _0}}}\frac{{\partial \rho }}{{\partial x}} + \frac{{{\tau _{sx}}}}{{{\rho _0}}} - \frac{{{\tau _{bx}}}}{{{\rho _0}}} - \frac{1}{{{\rho _0}}}\left( {\frac{{\partial {s_{xx}}}}{{\partial x}} + \frac{{\partial {s_{xy}}}}{{\partial y}}} \right) + \\ \frac{\partial }{{\partial x}}\left( {h{T_{xx}}} \right) + \frac{\partial }{{\partial y}}\left( {h\;{T_{xy}}} \right) + h\;{u_s}S \end{array} | (2) |
| \begin{array}{l} \frac{{\partial h\bar v}}{{\partial t}} + \frac{{\partial h\overline {uv} }}{{\partial x}} + \frac{{\partial h{{\overline v }^2}}}{{\partial y}} = f\bar uh - gh\frac{{\partial \eta }}{{\partial y}} - \frac{h}{{{\rho _0}}}\frac{{\partial {p_a}}}{{\partial y}} - \frac{{g{h^2}}}{{2{\rho _0}}}\frac{{\partial \rho }}{{\partial y}} + \frac{{{\tau _{sy}}}}{{{\rho _0}}} - \frac{{{\tau _{by}}}}{{{\rho _0}}} - \frac{1}{{{\rho _0}}}\left( {\frac{{\partial {s_{yx}}}}{{\partial x}} + \frac{{\partial {s_{yy}}}}{{\partial y}}} \right) + \\ \frac{\partial }{{\partial x}}\left( {h{T_{xy}}} \right) + \frac{\partial }{{\partial y}}\left( {h\;{T_{yy}}} \right) + h\;{v_s}S \end{array} | (3) |
式中:t为时间;x,y为笛卡尔坐标系坐标;η为水位;h为总水深;u,v为x,y方向上的速度分量;f为科里奥利力系数;S为源项;T为水平粘滞应力项,包括粘性力、紊流应力和水平对流,根据沿水深平均的速度梯度用涡流粘性方程得出.
2.2.7 数值解法(1)空间离散
计算区域的空间离散是用有限体积法(Finite Volmne Method),将该连续统一体细分为不重叠的单元,单元可以是任意形状的多边形,但在这里只考虑三角形和四边形单元. 浅水方程组的通用形式一般可以写成
| \frac{{\partial U}}{{\partial t}} + \nabla \cdot \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{U}} \right) = \mathit{\boldsymbol{S}}\left( \mathit{\boldsymbol{U}} \right) | (4) |
式中:U为守恒型物理向量;F为通量向量;S为源项.
在笛卡尔坐标系中,二维浅水方程组可以写为:
| \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \left( {\mathit{\boldsymbol{F}}_x^I - \mathit{\boldsymbol{F}}_x^V} \right)}}{{\partial x}} + \frac{{\partial \left( {\mathit{\boldsymbol{F}}_y^I - \mathit{\boldsymbol{F}}_y^V} \right)}}{{\partial y}} = \mathit{\boldsymbol{S}} | (5) |
式中:上标I和V分别为无粘性和粘性通量. 各项分别如下:
| \boldsymbol{U = }\left[ {\begin{array}{*{20}{c}} h\\ {h\bar u}\\ {h\bar v} \end{array}} \right],\boldsymbol{F}_x^I = \left[ {\begin{array}{*{20}{c}} {h\bar u}\\ {h{{\bar u}^2} + \frac{1}{2}g\left( {{h^2} - {d^2}} \right)}\\ {h\;\overline {uv} } \end{array}} \right],\boldsymbol{F}_x^V = \left[ {\begin{array}{*{20}{c}} 0\\ {h\boldsymbol{A}\left( {2\frac{{\partial \bar u}}{{\partial x}}} \right)}\\ {h\boldsymbol{A}\left( {\frac{{\partial \bar u}}{{\partial y}} + \frac{{\partial \bar v}}{{\partial x}}} \right)} \end{array}} \right] | (6) |
| \boldsymbol{F}_y^I = \left[ {\begin{array}{*{20}{c}} {h\bar v}\\ {h\overline {uv} }\\ {h{{\bar v}^2} + \frac{1}{2}g\left( {{h^2} - {d^2}} \right)} \end{array}} \right],F_y^V = \left[ {\begin{array}{*{20}{c}} 0\\ {hA\left( {\frac{{\partial \bar u}}{{\partial y}} + \frac{{\partial \bar v}}{{\partial x}}} \right)}\\ {hA\left( {2\frac{{\partial \bar v}}{{\partial x}}} \right)} \end{array}} \right] | (7) |
| \boldsymbol{S} = \left[ {\begin{array}{*{20}{c}} 0\\ {g\eta \frac{{\partial d}}{{\partial x}} + f\bar vh - \frac{h}{{{\rho _0}}}\frac{{\partial {\rho _a}}}{{\partial x}} - \frac{{g{h^2}}}{{2{\rho _0}}}\frac{{\partial \rho }}{{\partial y}} - \frac{1}{{{\rho _0}}}\left( {\frac{{\partial {s_{xx}}}}{{\partial x}} + \frac{{\partial {s_{xy}}}}{{\partial y}}} \right) + \frac{{{\tau _{sx}}}}{{{\rho _0}}} - \frac{{{\tau _{bx}}}}{{{\rho _0}}} + h{u_s}}\\ {g\eta \frac{{\partial d}}{{\partial y}} + f\bar uh - \frac{h}{{{\rho _0}}}\frac{{\partial {\rho _a}}}{{\partial y}} - \frac{{g{h^2}}}{{2{\rho _0}}}\frac{{\partial \rho }}{{\partial y}} - \frac{1}{{{\rho _0}}}\left( {\frac{{\partial {s_{yx}}}}{{\partial x}} + \frac{{\partial {s_{yy}}}}{{\partial y}}} \right) + \frac{{{\tau _{sy}}}}{{{\rho _0}}} - \frac{{{\tau _{by}}}}{{{\rho _0}}} + h{v_s}} \end{array}} \right] | (8) |
对方程第i个单元积分,并运用Gauss原理重写可得出:
| \int_{{A_i}} {\frac{{\partial U}}{{\partial t}}} d\Omega + \int_{{\Gamma _i}} {\left( {\mathit{\boldsymbol{F}} \cdot \mathit{\boldsymbol{n}}} \right)ds = \int_{{A_i}} {\mathit{\boldsymbol{S}}\left( \mathit{\boldsymbol{U}} \right)d\Omega } } | (9) |
式中:Ai为单元Ωi的面积;Γi为单元的边界;ds为沿着边界的积分变量. 这里使用单点求积法来计算面积的积分,该求积点位于单元的质点,同时使用中点求积法来计算边界积分,方程可以写为
| \frac{{\partial {U_i}}}{{\partial t}} + \frac{1}{{{A_i}}}\sum\limits_j^{NS} {\mathit{\boldsymbol{F}} \cdot \mathit{\boldsymbol{n}}\Delta {\mathit{\Gamma }_j}} = {S_i} | (10) |
式中:Ui和Si分别为第i个单元的U和S的平均值,并位于单元中心;NS是单元的边界数;ΔΓj为第j个单元的长度.
一阶解法和二阶解法都可以用于空间离散求解. 对于二维的情况,近似的Riemann解法可以用来计算单元界面的对流流动. 使用Roe方法时,界面左边的和右边的相关变量需要估计取值. 二阶方法中,空间准确度可以通过使用线性梯度重构的技术来获得. 而平均梯度可以用由Jawahar和Kamath于2000年提出的方法来估计,为了避免数值振荡,模型使用了二阶TVD格式.
(2)时间积分
考虑方程的一般形式:
| \frac{{\partial U}}{{\partial t}} = G\left( \mathit{\boldsymbol{U}} \right) | (11) |
对于二维模拟,浅水方程的求解有两种方法:一种是低阶方法,另一种是高阶方法. 本研究采用高阶的方法,为以如下形式的使用了二阶的Runge Kutta方法:
| {\mathit{\boldsymbol{U}}_{n + 1/2}} = {\mathit{\boldsymbol{U}}_n} + \frac{1}{2}\Delta t\mathit{\boldsymbol{G}}\left( {{\mathit{\boldsymbol{U}}_n}} \right) | (12) |
| {\mathit{\boldsymbol{U}}_{n + 1}} = {\mathit{\boldsymbol{U}}_n} + \Delta t\mathit{\boldsymbol{G}}\left( {{\mathit{\boldsymbol{U}}_{n + 1/2}}} \right) | (13) |
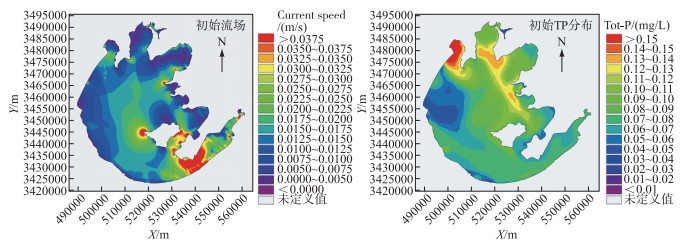
为模拟更符合实际情况,采取随空间变化的流场和总磷分布场作为计算的初始状态. 本研究预先按照平均年的水文、水质条件进行计算了一年,作为模拟开始时的初始条件,见附图Ⅴ.
|
附图Ⅴ 模拟的初始值 AttachedFig5 Initial value of simulation |
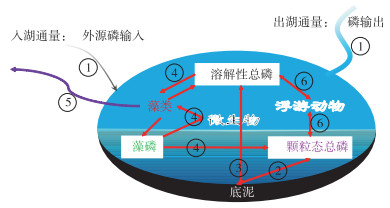
本研究在模拟磷浓度的变化时,除了计算磷随流场的迁移扩散外,还综合考虑了以下过程(附图Ⅵ):①磷通量出湖与入湖;②湖内颗粒态磷的沉降与悬浮;③湖内底泥对溶解态总磷的吸附与释放;④湖内藻类生长与死亡对颗粒态磷及溶解态磷的影响;⑤藻类打捞及水生植物收割对颗粒态磷及溶解态磷的影响;⑥浮游动物生长与死亡对颗粒态磷及溶解态磷的影响. 以上磷在湖内的循环过程见示意附图Ⅵ.
|
附图Ⅵ 磷循环模型原理示意图 AttachedFig6 Schematic diagram of the model |
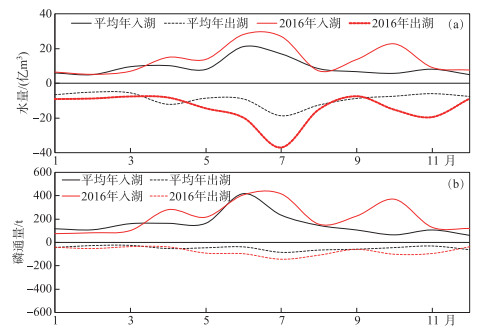
本研究使用2016年逐月各段面太湖出入湖水量和磷通量数据进行模型建立与率定. 建立好的模型使用平均年数据模拟太湖的一般状态,在此基础上设置新孟河引水的不同排水路线. 平均年太湖入湖水量111亿m3,比2016年减少52亿m3,出湖水量105亿m3,比2016年减少64亿m3. 平均年太湖入湖磷通量1958 t,比2016年减少611 t,出湖磷通量638 t,比2016年减少300 t(附图Ⅶ).
|
附图Ⅶ 太湖逐月出入湖水量、磷通量 AttachedFig7 Monthly inflow and outflow of Lake Taihu and phosphorus flux |
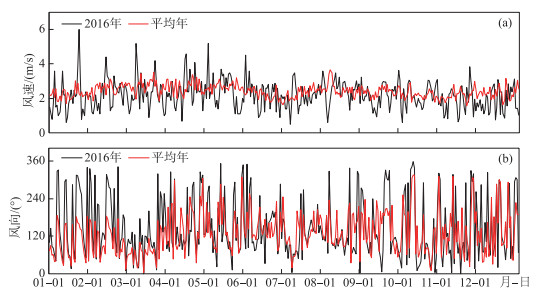
本研究使用2016年无锡站逐小时风速、风向数据进行模型建立与率定. 统计2007 2020年无锡站逐小时盛行风向和平均风速作为平均年数据(附图Ⅷ),模拟太湖的一般状态.
|
附图Ⅷ 太湖逐小时风速、风向 AttachedFig8 Hourly wind speed and direction in Lake Taihu |
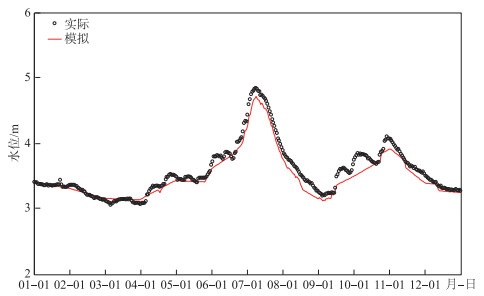
本研究通过比较2016年太湖内实测与模拟水位来率定水动力子模型精度,通过比较2016年太湖实测与模拟的水中总磷存量以及各湖区中心测点的逐月TP浓度来率定磷循环子模型精度.
太湖内实测与模拟水位的均方根误差为0.11 m,纳什系数为0.91(附图Ⅸ),因此本研究建立的水动力子模型对太湖出入湖流量的模拟是准确的.
|
附图Ⅸ 太湖水位验证 AttachedFig9 Validation of water levels in Lake Taihu |
在太湖各湖区的中心选取一个测点,将模拟与实测的2016年逐月TP浓度绘制于附图Ⅹ,模拟中与实测值的变化趋势接近,说明本研究建立的磷循环子模型对太湖内磷变化过程的模拟是基本准确的. 从各湖区总磷浓度变化来看,模拟值与实测值趋势一致,反映了2016年磷升高的过程,本研究建立的磷循环子模型对太湖内磷变化过程的模拟是基本准确的.

|
附图Ⅹ 太湖各湖区监测点位总磷浓度验证 AttachedFig10 Validation of TP at monitoring points in Lake Taihu |
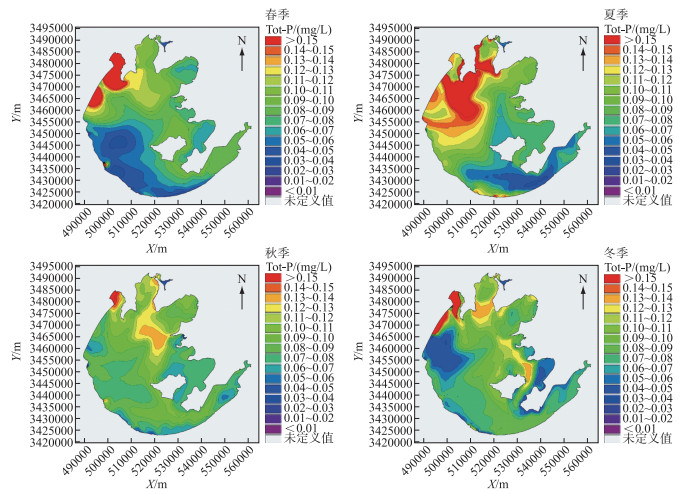
基于平均年的水文、水质数据,本研究将平均年且新孟河未引水的各季节最后一天的太湖总磷浓度分布绘制于附图Ⅺ,由附图Ⅺ可见,春季竺山湖、西部沿岸区TP较高,夏季全湖TP显著上升,秋季全湖TP比夏季下降,冬季全湖TP接近春季,只有竺山湖TP较高.
| 附表Ⅰ 模型精度 Appendix Ⅰ Model calibration |
|
附图Ⅺ 平均年各季节太湖总磷浓度分布 AttachedFig11 Distribution of TP in Lake Taihu in each season |
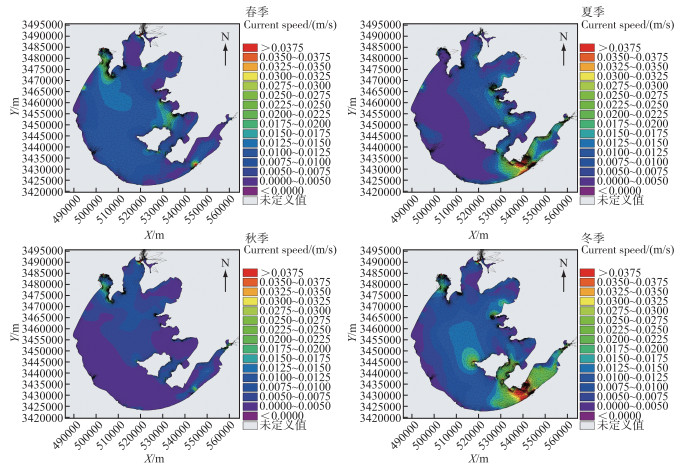
基于平均年的水文数据,本研究将4种调水工况及无引水情况各季节最后一天的太湖流场绘制附图Ⅻ~ 图ⅩⅥ. 在本研究中,为反映太湖风场的一般性规律,我们统计2007 2020年无锡站逐小时的风场数据,以统计时间内每小时出现最多的风向和平均风速作为平均年的风场. 因此模型中风场的风速和风向是逐小时变化的,从而引起流场也是变化的.

|
附图Ⅻ 无引水情况太湖各季节流场 AttachedFig12 Seasonal flow field of Lake Taihu without water diversion |
|
附图ⅩⅢ 方案一太湖各季节流场 AttachedFig13 Seasonal flow field of Lake Taihu under Scheme one |
|
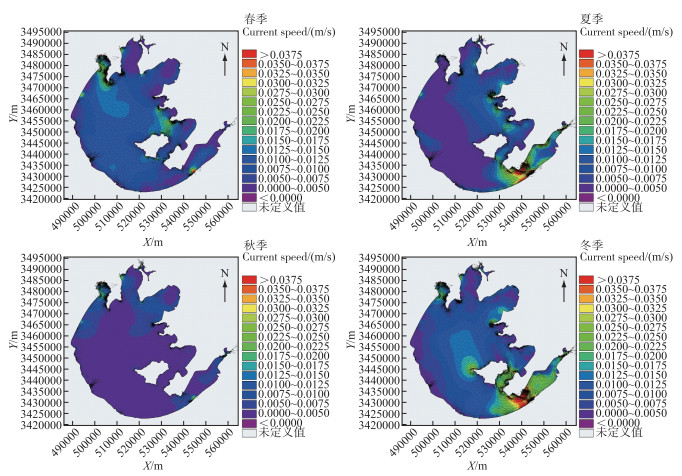
图ⅩⅣ 方案二太湖各季节流场 AttachedFig14 Seasonal flow field of Lake Taihu under Scheme two |
|
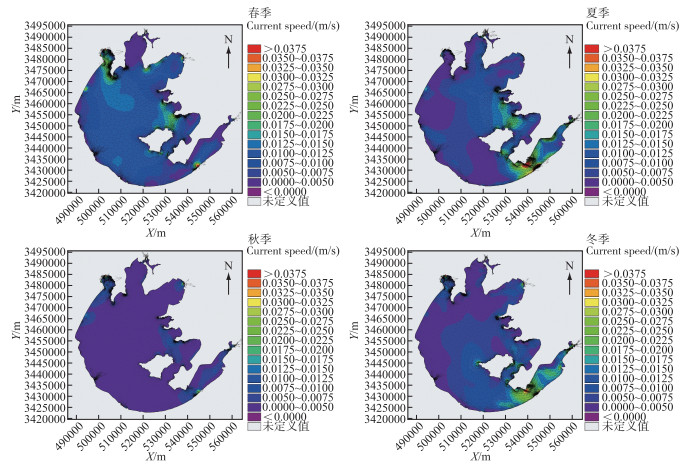
附图ⅩⅤ 方案三太湖各季节流场 AttachedFig15 Seasonal flow field of Lake Taihu under Scheme three |
|
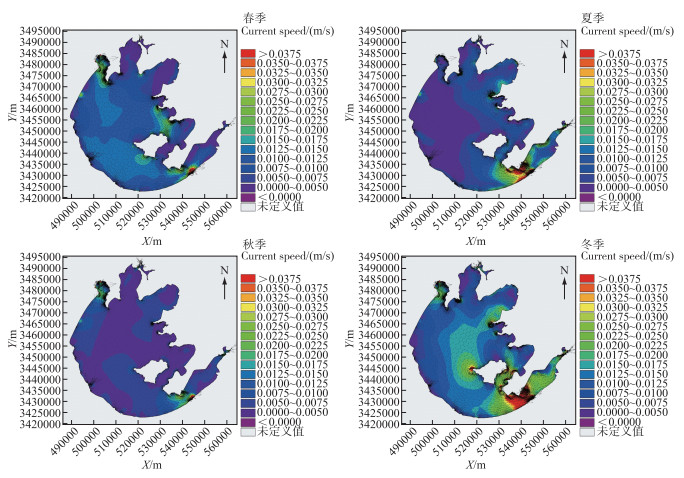
附图ⅩⅥ 方案四太湖各季节流场 AttachedFig16 Seasonal flow field of Lake Taihu under Scheme four |
| [1] |
Wu HY. Study on key technologies of Yangtze-Taihu Water Diversion. China Water Resources, 2008(1): 6-8. [吴浩云. 引江济太调水试验关键技术研究和应用. 中国水利, 2008(1): 6-8.] |
| [2] |
Zhai SH, Zhang HJ, Hu WP et al. Evaluation on result of Yangtze-Taihu water diversion. China Water Resources, 2008(1): 21-23. [翟淑华, 张红举, 胡维平等. 引江济太调水效果评估. 中国水利, 2008(1): 21-23.] |
| [3] |
National Development and Reform Commission of the People's Republic of China ed. The overall plan for the comprehensive management of the water environment of the Taihu River Basin (revised in 2013). [中华人民共和国国家发展和改革委员会. 太湖流域水环境综合治理总体方案(2013年修编). ]
|
| [4] |
Zhu GW, Zou W, Guo CX et al. Long-term variations of phosphorus concentration and capacity in Lake Taihu, 2005-2018: Implications for future phosphorus reduction target management. J Lake Sci, 2020, 32(1): 21-35. [朱广伟, 邹伟, 国超旋等. 太湖水体磷浓度与赋存量长期变化(2005-2018年)及其对未来磷控制目标管理的启示. 湖泊科学, 2020, 32(1): 21-35. DOI:10.18307/2020.0103] |
| [5] |
Zhu W, Hu SY, Feng GY et al. Effects of great floods on phosphorus in shallow lakes: A case study of Lake Taihu in 2016. J Lake Sci, 2020, 32(2): 325-336. [朱伟, 胡思远, 冯甘雨等. 特大洪水对浅水湖泊磷的影响: 以2016年太湖为例. 湖泊科学, 2020, 32(2): 325-336. DOI:10.18307/2020.0201] |
| [6] |
Wang H, Chen HX, Xu ZA et al. Variation trend of total phosphorus and its controlling factors in Lake Taihu, 2010-2017. J Lake Sci, 2019, 31(4): 919-929. [王华, 陈华鑫, 徐兆安等. 2010-2017年太湖总磷浓度变化趋势分析及成因探讨. 湖泊科学, 2019, 31(4): 919-929. DOI:10.18307/2019.0421] |
| [7] |
Wu Z, Wu SF, Liu Y et al. Key processes and mechanisms of nitrogen and phosphorus cycling in lakes. Acta Scientiarum Naturalium Universitatis Pekinensis, 2018, 54(1): 218-228. [吴桢, 吴思枫, 刘永等. 湖泊氮磷循环的关键过程与定量识别方法. 北京大学学报: 自然科学版, 2018, 54(1): 218-228. DOI:10.13209/j.0479-8023.2017.143] |
| [8] |
Yang Z. Advances in factors influencing release of nitrogen and phosphorus in sediments. Environmental Science Survey, 2017, 36(A1): 16-19, 29. [杨赵. 湖泊沉积物中氮磷源-汇现象影响因素研究进展. 环境科学导刊, 2017, 36(A1): 16-19, 29.] |
| [9] |
Taihu Basin Authority of Ministry of Water Resources ed. The health status report of Lake Taihu. 2018. [水利部太湖流域管理局. 太湖健康状况报告. 2018. ]
|
| [10] |
Zhu W, Xue ZP, Zhang YM et al. Effect of water diversion from the Yangtze River to Lake Taihu on total phosphorus rebound after 2016. J Lake Sci, 2020, 32(5): 1432-1445. [朱伟, 薛宗璞, 章元明等. "引江济太"对2016年后太湖总磷反弹的直接影响分析. 湖泊科学, 2020, 32(5): 1432-1445. DOI:10.18307/2020.0518] |
| [11] |
Zhu W, Cheng L, Xue ZP et al. Changes of water exchange cycle in Lake Taihu (1986-2018) and its effect on the spatial pattern of water quality. J Lake Sci, 2021, 33(4): 1087-1099. [朱伟, 程林, 薛宗璞等. 太湖水体交换周期变化(1986-2018年)及对水质空间格局的影响. 湖泊科学, 2021, 33(4): 1087-1099. DOI:10.18307/2021.0411] |
| [12] |
Zhao XF, Xu HL. Study on vegetation change of Taitemar Lake during ecological water transfer. Environmental Monitoring and Assessment, 2019, 191(10): 1-11. DOI:10.1007/s10661-019-7664-0 |
| [13] |
Su HB, Zhang TM, Hu CY. Environmental impact assessment on water diversion project based on ecological footprint: Case of Niulan River-Dianchi water supplement project. Yangtze River, 2015, 46(10): 48-51. [苏红兵, 张天明, 胡朝英. 基于生态足迹的调水工程环境影响评价——以牛栏江-滇池补水工程为例. 人民长江, 2015, 46(10): 48-51.] |
| [14] |
Huang JC, Yan RH, Gao JF et al. Modeling the impacts of water transfer on water transport pattern in Lake Chao, China. Ecological Engineering, 2016, 95: 271-279. DOI:10.1016/j.ecoleng.2016.06.074 |
| [15] |
Hua ZL, Gu L, Xue H et al. Assessing indicators for water diversion based on improving water quality of shallow lakes. J Lake Sci, 2008, 20(5): 623-629. [华祖林, 顾莉, 薛欢等. 基于改善水质的浅水湖泊引调水模式的评价指标. 湖泊科学, 2008, 20(5): 623-629. DOI:10.18307/2008.0511] |
| [16] |
Li YP, Acharya K, Yu ZB. Modeling impacts of Yangtze River water transfer on water ages in Lake Taihu, China. Ecological Engineering, 2011, 37(2): 325-334. DOI:10.1016/j.ecoleng.2010.11.024 |
| [17] |
Yan K, Yuan ZW, Goldberg S et al. Phosphorus mitigation remains critical in water protection: A review and meta-analysis from one of China's most eutrophicated lakes. Science of the Total Environment, 2019, 689: 1336-1347. DOI:10.1016/j.scitotenv.2019.06.302 |
| [18] |
Elshemy M, Khadr M, Atta Y et al. Hydrodynamic and water quality modeling of Lake Manzala (Egypt) under data scarcity. Environmental Earth Sciences, 2016, 75(19): 1-13. DOI:10.1007/s12665-016-6136-x |
| [19] |
Taihu Basin Authority of Ministry of Water Resources ed. Annual report on the diversion of the river from Lake Taihu Basin, 2011. [水利部太湖流域管理局. 太湖流域引江济太年报, 2011. ]
|
| [20] |
Hu WP, Pu PM, Qin BQ. A three-dimensional numerical simulation on the dynamics in Taihu Lake, China (Ⅰ): The water level and the current during the 9711 Typhoon Process. J Lake Sci, 1998, 10(4): 17-25. [胡维平, 濮培民, 秦伯强. 太湖水动力学三维数值试验研究——1.风生流和风涌增减水的三维数值模拟. 湖泊科学, 1998, 10(4): 17-25. DOI:10.18307/1998.0403] |
| [21] |
Xu H, McCarthy MJ, Paerl HW et al. Contributions of external nutrient loading and internal cycling to cyanobacterial bloom dynamics in Lake Taihu, China: Implications for nutrient management. Limnology and Oceanography, 2021, 66(4): 1492-1509. DOI:10.1002/lno.11700 |
 2022, Vol. 34
2022, Vol. 34 


