水资源承载力(water resource carrying capacity, WRCC)可认为是在临近破坏水资源可持续利用时水资源所能持续支撑区域的最大经济社会发展规模，水资源承载力评价是水资源承载力障碍因子诊断识别、水资源承载力预警调控的重要前期工作，是水资源承载力研究中关键组成部分^[1]. 从物理成因的角度看，区域水资源承载力就是在水资源承载调控力作用下水资源承载支撑力与水资源承载压力之间的动态平衡关系. 水资源承载力评价是水资源、社会经济和生态环境三大系统相作用下一种定量的水资源安全测度，是水资源空间均衡评价的基础，合理、准确地评价区域水资源承载状况是水资源管理决策的科学依据，在经济社会高质量发展、生态环境保护、水资源空间均衡等方面具有重要意义^[2]. 由于水资源承载力系统包含水资源承载主体、客体及二者间的复杂作用，充满着未确知性、随机性和模糊性，具有明显的不确定性动态变化特征，是近年来国内外水资源研究领域的热点和难点，深受学者们的关注. 目前，区域水资源承载力评价方法主要有模糊综合评价法^[3]、主成分分析法^[4]、系统动力学法^[5]、灰色关联法^[6]、集对分析法^[7]等. 其中集对分析法因可深刻、全面地解析和定量表达评价样本数据与评价等级间的符合关系程度信息，为水资源承载力评价提供了有效途径而开始被广泛应用，反映水资源承载力评价样本与评价等级标准这一集对的复杂系统结构的单指标联系数计算是集对分析法中的重要一环. 确定联系数的现有方法仅从宏观上考虑了评价指标值与评价等级间的联系程度，而对于联系数系统结构中联系数分量间的微观运动对这种联系程度的影响考虑较少，使得区域水资源承载力评价结果可能发生偏差. 此外，目前确定联系数中差异度系数I的方法主要有传统取值法^[8]、三角模糊数法^[9]和灰色关联度法^[10]等，传统取值法和灰色关联法强调如何确定差异度系数I的具体数值，如对三元联系数有差异度系数I=0，未考虑差异度系数I的变化特性，现有的三角模糊数法强调静态取值，如差异度系数的三角模糊数一般取I=(-0.5, 0, 0.5)、未考虑差异度系数I随实际评价样本值的动态变化特征. 针对上述联系数系统结构中联系数分量迁移、转化的矛盾运动和差异度系数动态性考虑不足等问题，为更准确和客观地评价区域水资源承载力，本文综合运用集对分析联系数、偏联系数、半偏联系数、减法集对势和三角模糊数等方法，构造刻画联系数系统结构内联系数分量间微观运动的迁移率矩阵，探索联系数系统结构及其动态演化机制，进而提出一种联系数分量值的修正方法，同时采用减法集对势和三角模糊数相结合的方法确定差异度系数I，由此构建基于半偏联系数和动态减法集对势的区域水资源承载力评价方法并应用于安徽省淮北市水资源承载力评价中.

1 基于半偏联系数和动态减法集对势的区域水资源承载力评价方法的建立

综合运用集对分析联系数、偏联系数、半偏联系数、减法集对势和三角模糊数方法构建基于半偏联系数和动态减法集对势的区域水资源承载力评价方法，该方法的建立过程包括以下6个步骤：

步骤1：确定区域水资源承载力评价指标体系及评价等级标准. 根据区域水资源承载支撑力、承载压力和承载调控力相作用形成区域水资源承载状态这一机理进行水资源承载力系统结构分析^[11]，结合研究区域特点以及专家咨询、文献调研等方法，建立区域水资源承载力评价指标体系{x_jk|j=1, 2, …, n_k; k=1, 2, 3}和评价等级标准{s_gj|g=1, 2, …, n_g; j=1, 2, …, n_j}，相应的评价指标样本数据集记为{x_ijk|i=1, 2, …, n_i; j=1, 2, …, n_k; k=1, 2, 3}. 其中，x_ijk为水资源承载力评价指标体系中样本i子系统k指标j的数值，n_i为评价样本数目、n_k为子系统k中评价指标数目，显然有n₁+n₂+n₃=n_j，n_g为评价等级数目^[11]. 不失一般性，这里取3个评价等级即n_g=3，1级、2级、3级分别表示水资源“可载”“临界”和“超载”.

步骤2：计算区域水资源承载力评价样本单指标值联系数. 集对分析(set pair analysis，SPA)是由中国学者赵克勤先生1989年提出的联系数学方法^[8]，它将问题的确定性和不确定性整合到统一的结论中，可研究系统各要素与整个系统之间的内在关系. SPA建立了有关联的两集合(集对系统)之间符合某属性的确定性和不确定性关系程度的系统关系结构模型^[12]，其中三元联系数的表达式为^[8]：

$ u = a + bI + cJ $

(1)

式中，a、b、c分别为三元联系数同一度、差异度和对立度分量，它们组成集对系统的关系结构，反映集对系统符合所研究属性的本质，I为差异度系数，J为对立度系数. 式(1)建立了SPA的基本模型. 对给出的区域水资源承载力评价指标的数值与评价等级1、2、3级进行模糊关系的匹配，从而得到评价样本i子系统k指标j的样本值x_ijk与评价等级标准s_gj之间联系数(接近程度)u_ijkg.

对随指标值x_ijk增大而其评价等级g增大的指标(正向指标)，三元联系数计算式为^{[8, 13]}：

$ \left\{ {\begin{array}{*{20}{l}} {{u_{ijk1}} = 1}\\ {{u_{ijk2}} = 1 - 2\left( {{s_{1j}} - {x_{ijk}}} \right)/\left( {{s_{1j}} - {s_{0j}}} \right)\quad , {s_{0j}} < {x_{ijk}} \le {s_{1j}}}\\ {{u_{ijk3}} = - 1} \end{array}} \right. $

(2)

$ \left\{ {\begin{array}{*{20}{l}} {{u_{ijk1}} = 1 - 2\left( {{x_{ijk}} - {s_{1j}}} \right)/\left( {{s_{2j}} - {s_{1j}}} \right)}\\ {{u_{ijk2}} = 1}\\ {{u_{ijk3}} = 1 - 2\left( {{s_{2j}} - {x_{ijk}}} \right)/\left( {{s_{2j}} - {s_{1j}}} \right)} \end{array}\quad , {s_{1j}} < {x_{ijk}} \le {s_{2j}}} \right. $

(3)

$ \left\{ {\begin{array}{*{20}{l}} {{u_{ijk1}} = - 1}\\ {{u_{ijk2}} = 1 - 2\left( {{x_{ijk}} - {s_{2j}}} \right)/\left( {{s_{3j}} - {s_{2j}}} \right)\quad , {s_{2j}} < {x_{ijk}} \le {s_{3j}}}\\ {{u_{ijk3}} = 1} \end{array}} \right. $

(4)

对随指标值x_ijk增大而其评价等级g减小的指标(反向指标)，三元联系数计算式为^{[8, 13]}：

$ \left\{ {\begin{array}{*{20}{l}} {{u_{ijk1}} = 1}\\ {{u_{ijk2}} = 1 - 2\left( {{s_{1j}} - {x_{ijk}}} \right)/\left( {{s_{1j}} - {s_{0j}}} \right)\quad , {s_{0j}} > {x_{ijk}} \ge {s_{1j}}}\\ {{u_{ijk3}} = - 1} \end{array}} \right. $

(5)

$ \left\{ {\begin{array}{*{20}{l}} {{u_{ijk1}} = 1 - 2\left( {{x_{ijk}} - {s_{1j}}} \right)/\left( {{s_{2j}} - {s_{1j}}} \right)}\\ {{u_{ijk2}} = 1}\\ {{u_{ijk3}} = 1 - 2\left( {{s_{2j}} - {x_{ijk}}} \right)/\left( {{s_{2j}} - {s_{1j}}} \right)} \end{array}\quad , {s_{1j}} > {x_{ijk}} \ge {s_{2j}}} \right. $

(6)

$ \left\{ {\begin{array}{*{20}{l}} {{u_{ijk1}} = - 1}\\ {{u_{ijk2}} = 1 - 2\left( {{x_{ijk}} - {s_{2j}}} \right)/\left( {{s_{3j}} - {s_{2j}}} \right)\quad , {s_{2j}} > {x_{ijk}} \ge {s_{3j}}}\\ {{u_{ijk3}} = 1} \end{array}} \right. $

(7)

式中，{s_0j、s_1j}、{s_1j、s_2j}、{s_2j、s_3j}分别为评价等级1级、2级、3级的门限区间端点值，对正向指标有s_0j < s_1j < s_2j < s_3j，对反向指标有s_0j>s_1j> s_2j> s_3j. 联系数u_ijkg显然可作为样本值x_ijk与评价等级标准s_gj间接近程度这一可变模糊关系的一种相对差异度函数，相应的相对隶属度为^[11]：

$ v_{ijkg}^ * = 0.5 + 0.5{u_{ijkg}}\quad \left( {i = 1, 2, \cdots , {n_i};j = 1, 2, \cdots , {n_k};k = 1, 2, 3;g = 1, 2, 3} \right) $

(8)

于是，由式(8)经归一化^[11]可得水资源承载力评价指标值联系数分量v_ijkg，g=1, 2, 3：

$ {v_{ijkg}} = v_{ijkg}^ * /\left( {v_{ijk1}^ * + v_{ijk2}^ * + v_{ijk3}^ * } \right) $

(9)

由联系数分量v_ijkg可构成评价单指标值联系数u_ijk^[11]：

$ {u_{ijk}} = {v_{ijk1}} + {v_{ijk2}}I + {v_{ijj3}}J $

(10)

式中，I、J含义同式(1).

步骤3：基于偏联系数迁移率矩阵^[14-15]的构建及评价样本指标值联系数的计算. 评价样本的单指标值联系数分量v_ijk1、v_ijk2、v_ijk3宏观上实际反映的是水资源承载状态的同、异、反的数值，但从水资源承载力评价这一问题背景看，v_ijk1、v_ijk2、v_ijk3分别定量刻画和描述了该样本中某个单指标值隶属于水资源承载力等级1、2、3的程度，实现了水资源承载力这一复杂系统中评价指标样本值与评价等级间符合程度的模糊关系表达. 实际上联系数分量同、异、反之间具有相互迁移、相互转化的动态演化特性. 根据自然和社会领域联系的普遍性、运动的绝对性、矛盾的普遍性哲学原理，联系数分量总是存在着同、异、反不同对立层次及其相互迁移、转化，由此构成联系数的同异反系统结构，显然在这系统结构内各联系数分量不再是相互独立的量，而是通过微观层次上的矛盾运动相互影响^{[8, 12, 14]}. 现有研究中大多数是在计算得到联系数分量后，未考虑联系数分量间相互迁移、转化(动态演化)的联系数系统关系结构特征，而是直接采用联系数分量值(如最大隶属度法、属性识别法、级别特征值法)进行实际问题的综合评价，所得结果的稳定性缺乏验证.

可见，如何定量刻画和表达联系数系统结构中联系数分量这种微观层次上的动态演化所产生的影响，直观看到系统在宏观静态下的微观运动、迁移及其结果，从而更客观和准确地把握这种迁移运动规律，深刻揭示集对系统的本质特征十分关键. 偏联系数^[16]、半偏联系数^[17]着眼于集对系统关系结构^[12]在微观层次上的动态演化，可定量刻画联系数分量间的微观运动. 以三元联系数u=a+bI+cJ为例，一阶偏正联系数为^[18]：

$ {\partial ^ + }\mu = {\partial ^ + }a + {\partial ^ + }b{i^ + } = \frac{a}{{a + b}} + \frac{b}{{b + c}}{i^ + } $

(11)

式中，${\partial ^ + }a = \frac{a}{{a + b}}$、${\partial ^ + }b = \frac{b}{{b + c}}$分别称为联系数分量a、b的一阶偏正联系数. 其中∂⁺a的含义可认为当前的a原本处在b层次，是从b层次朝正向同迁移而来，∂⁺b的含义可认为当前的b原本处在c层次，是从c层次朝正向异迁移而来^[18]，它们都可以称为半偏联系数. 类似地，一阶偏负联系数为^[18]：

$ {\partial ^ - }\mu = {\partial ^ - }b{i^ - } + {\partial ^ - }cj = \frac{b}{{a + b}}{i^ - } + \frac{c}{{b + c}}j $

(12)

式中，${\partial ^ - }b = \frac{b}{{a + b}}$、${\partial ^ - }c = \frac{c}{{b + c}}$分别称为联系数分量b、c的一阶偏负联系数. 其中∂^-b的含义可认为当前的b原本也处在a层次，是从a层次朝负向异迁移而来，∂^-c的含义是可认为当前的c原本处在b层次，是从b层次朝负向反迁移而来^[18]，它们也都可以称为半偏联系数. 偏联系数^[16]可揭示联系数分量在微观层次上的矛盾运动并可定量表达集对系统结构中各联系数分量的相互迁移、转化(动态演化). 可见，偏联系数作为联系数的一种伴随函数，可实现系统结构内联系数分量在宏观静态下微观层次上运动方向和增量大小的定性、定量刻画，以系统结构内联系数分量为驱动对象，以联系数分量存储的“信息能”为驱动力，以向不同对立层次迁移为驱动方向，实现联系数分量的更新、迭代，从而更合理准确地确定联系数并深刻认识微观运动规律^[16].

据此，这里参考联系数伴随函数特别是偏联系数的基本概念和内涵，将偏联系数、半偏联系数应用于刻画水资源承载力评价样本各联系数分量间相互迁移运动，进而得到修正后的联系数分量，进一步增强水资源承载力评价的合理性和准确性^[14]. 参考文献[14-15]结合偏联系数构建迁移率矩阵$X = \left[ {\begin{array}{*{20}{c}} 1&{{\partial ^ - }b}&{{\partial ^ - }b{\partial ^ - }c}\\ {{\partial ^ + }a}&1&{{\partial ^ - }c}\\ {{\partial ^ + }b{\partial ^ + }a}&{{\partial ^ + }b}&1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{\frac{b}{{a + b}}}&{\frac{b}{{a + b}}\frac{c}{{b + c}}}\\ {\frac{a}{{a + b}}}&1&{\frac{c}{{b + c}}}\\ {\frac{b}{{b + c}}\frac{a}{{a + b}}}&{\frac{b}{{b + c}}}&1 \end{array}} \right]$，其物理含义是^[14-15]：对于联系数分量a来说，存在着由分量a、b和c向a的微观动态运动，显然分量a向自身迁移转化的可能性为1，分量b和c都存在着向分量a的可能迁移运动，因此需要考虑分量b和c向分量a的迁移作用，∂⁺a反映了分量b向分量a的迁移率，b∂⁺a即为分量b向分量a迁移运动的数值，∂⁺b∂⁺a反映了分量c经分量b向分量a的迁移率，即分量c先向分量b转化再向分量a转化，分量b是连结分量a和c的桥梁，c∂⁺b∂⁺a为分量c向分量a迁移运动的数值. 由此并结合式(11)、(12)，可得到经半偏联系数转化修正后的同一度分量为$a + b\frac{a}{{a + b}} + c\frac{b}{{b + c}}\frac{a}{{a + b}}$.同理，对于联系数分量b来说，存在着由分量a、b和c向b的微观动态运动，经半偏联系数转化修正后的差异度分量为$b + a\frac{b}{{a + b}} + c\frac{b}{{b + c}}$，对于联系数分量c来说，存在着由分量a、b和c向c的微观动态运动，经半偏联系数转化修正后的对立度分量为$c + b\frac{c}{{b + c}} + a\frac{b}{{a + b}}\frac{c}{{b + c}}$，即原联系数矩阵U=[a, b, c]经迁移率矩阵X转化修正后的评价样本指标值联系数矩阵R^[14-15]为：

$ \begin{array}{c} R = UX = [a, b, c]\left[ {\begin{array}{*{20}{c}} 1&{\frac{b}{{a + b}}}&{\frac{b}{{a + b}}\frac{c}{{b + c}}}\\ {\frac{a}{{a + b}}}&1&{\frac{c}{{b + c}}}\\ {\frac{b}{{b + c}}\frac{a}{{a + b}}}&{\frac{b}{{b + c}}}&1 \end{array}} \right] = \\ \left[ {a + b\frac{a}{{a + b}} + c\frac{b}{{b + c}}\frac{a}{{a + b}}, b + a\frac{b}{{a + b}} + c\frac{b}{{b + c}}, c + b\frac{c}{{b + c}} + a\frac{b}{{a + b}}\frac{c}{{b + c}}} \right] \end{array} $

(13)

将式(10) 中的单指标联系数分量v_ijk1、v_ijk2和v_ijk3代入式(13)有^[14-15]：

$ \begin{array}{c} \left[ {{v_{ijk1}}, {v_{ijk2}}, {v_{ijk3}}} \right]\left[ {\begin{array}{*{20}{c}} 1&{\frac{{{v_{ijk2}}}}{{{v_{ijk1}} + {v_{ijk2}}}}}&{\frac{{{v_{ijk2}}}}{{{v_{ijk1}} + {v_{ijk2}}}}\frac{{{v_{ijk3}}}}{{{v_{ijk2}} + {v_{ijk3}}}}}\\ {\frac{{{v_{ijk1}}}}{{{v_{ijk1}} + {v_{ijk2}}}}}&1&{\frac{{{v_{ijk3}}}}{{{v_{ijk2}} + {v_{ijk3}}}}}\\ {\frac{{{v_{ijk2}}}}{{{v_{ijk2}} + {v_{ijk3}}}}\frac{{{v_{ijk11}}}}{{{v_{ijk1}} + {v_{ijk2}}}}}&{\frac{{{v_{ijk2}}}}{{{v_{ijk2}} + {v_{ijk3}}}}}&1 \end{array}} \right] = \\ \left[ {{v_{ijk1}} + {v_{ijk2}}\frac{{{v_{ijk1}}}}{{{v_{ijk1}} + {v_{ijk2}}}} + {v_{ijk3}}\frac{{{v_{ijk2}}}}{{{v_{ijk2}} + {v_{ijk3}}}}\frac{{{v_{ijk1}}}}{{{v_{ijk1}} + {v_{ijk2}}}}, {v_{ijk2}} + {v_{ijk1}}\frac{{{v_{ijk2}}}}{{{v_{ijk1}} + {v_{ijk2}}}} + {v_{ijk33}}\frac{{{v_{ijk2}}}}{{{v_{ijk2}} + {v_{ijk3}}}}, } \right.\\ \left. {{v_{ijk3}} + {v_{ijk2}}\frac{{{v_{ijk3}}}}{{{v_{ijk2}} + {v_{ijk3}}}} + {v_{ijk11}}\frac{{{v_{ijk2}}}}{{{v_{ijk1}} + {v_{ijk2}}}}\frac{{{v_{ijkk}}}}{{{v_{ijk2}} + {v_{ijk3}}}}} \right] \end{array} $

(14)

再对式(14)所得的联系数分量进行归一化^{[8, 11, 14]}得转化修正后的水资源承载力评价样本单指标值联系数u′_ijk：

$ u_{ijk}^\prime = v_{ijk1}^\prime + v_{ijk2}^\prime I + v_{ijk3}^\prime J $

(15)

式中，v′_ijk1、v′_ijk2、v′_ijk3分别为经迁移率矩阵转化并归一化后得到的水资源承载力评价样本单指标值联系数分量，这些分量是从联系数系统结构^[12]出发对评价样本单指标值联系数的一种动态修正结果，是宏观静止状态和微观运动状态综合作用得到的.

为更清晰地解析、把握联系数系统结构中各联系数分量这种微观运动的规律，探讨式(14)归一化后的水资源承载力评价样本单指标值联系数分量，较原联系数矩阵U =[a, b, c]中各分量的变化情况，这里不妨设：

① 原联系数矩阵U =[a, b, c]中最大的分量为同一度a，则有a≥0.5，由式(13)令修正后联系数分量的增量$\Delta a = b\frac{a}{{a + b}} + c\frac{b}{{b + c}}\frac{a}{{a + b}}, \Delta b = a\frac{b}{{a + b}} + c\frac{b}{{b + c}}, \Delta c = b\frac{c}{{b + c}} + a\frac{b}{{a + b}}\frac{c}{{b + c}}$，笔者认为归一化后的同一度分量小于原联系数同一度分量a，即有不等式$\frac{{a + \Delta a}}{{a + \Delta a + b + \Delta b + c + \Delta c}} < a$，证明如下：

要证$\frac{{a + \Delta a}}{{a + \Delta a + b + \Delta b + c + \Delta c}} < a \Leftrightarrow \frac{{a + \Delta a}}{{1 + \Delta a + \Delta b + \Delta c}} < a \Leftrightarrow a(\Delta a + \Delta b + \Delta c) - \Delta a > 0$，于是，$a\left( {b\frac{a}{{a + b}} + \left. {c\frac{b}{{b + c}}\frac{a}{{a + b}} + a\frac{b}{{a + b}} + c\frac{b}{{b + c}} + b\frac{c}{{b + c}} + a\frac{b}{{a + b}}\frac{c}{{b + c}}} \right) - b\frac{a}{{a + b}} - c\frac{b}{{b + c}}\frac{a}{{a + b}} > 0} \right.$整理可得，$\frac{{2abc + 2bc(a + b) + 2ab(b + c) - b(b + c) - bc}}{{(a + b)(b + c)}} > 0$，显然(a+b)(b+c)>0，则2abc+2bc(a+b)+2ab(b+c)－b(b+c)－bc>0，合并同类项可得，bc(4a+2b－1)+b(b+c)(2a－1)>0，由于a≥0.5，故4a+2b-1>0且2a-1≥0，即不等式bc(4a+2b－1)+b(b+c)(2a－1)>0成立，得证. 上述结果表明，如果三元联系数系统结构中同一度a最大，微观运动会使得同一度减小，减小的部分则向差异度b或对立度c迁移.

② 原联系数矩阵U =[a, b, c]中最大的分量为差异度b，则有b≥0.5，也满足此减小的规律：$\frac{{b + \Delta b}}{{a + \Delta a + b + \Delta b + c + \Delta c}} < b$，证明如下：

要证$\frac{{b + \Delta b}}{{a + \Delta a + b + \Delta b + c + \Delta c}} < b \Leftrightarrow \frac{{b + \Delta b}}{{1 + \Delta a + \Delta b + \Delta c}} < b \Leftrightarrow b(\Delta a + \Delta b + \Delta c) - \Delta b > 0$，于是，$b\left( {b\frac{a}{{a + b}} + \left. {c\frac{b}{{b + c}}\frac{a}{{a + b}} + a\frac{b}{{a + b}} + c\frac{b}{{b + c}} + b\frac{c}{{b + c}} + a\frac{b}{{a + b}}\frac{c}{{b + c}}} \right) - a\frac{b}{{a + b}} - c\frac{b}{{b + c}} > 0} \right.$整理可得，$\frac{{2abc + 2bc(a + b) + 2ab(b + c) - a(b + c) - c(a + b)}}{{(a + b)(b + c)}} > 0$，显然(a+b)(b+c)>0，则2abc+2bc(a+b)+ 2ab(b+c)－a(b+c)－c(a+b)>0，合并同类项可得，2abc+c(a+b)(2b－1)+a(b+c)(2b－1)>0，由于b≥0.5，故2b-1≥0，即不等式2abc+c(a+b)(2b－1)+a(b+c)(2b－1)>0，得证. 上述结果表明，如果三元联系数系统结构中差异度b最大，微观运动会使得差异度减小，减小的部分则会向同一度a或对立度c迁移.

③ 原联系数矩阵U=[a, b, c]中最大的分量为对立度c则有c≥0.5，由于三元联系数系统结构中，同一度分量a和对立度分量c是对称的，同理可证对立度减小的规律.

可见，在三元联系数的同异反系统结构中，联系数分量中的最大值，经微观迁移运动后该分量本身的值会减小，根据同异反分量之和为1，可知其他两个分量之和将增大，其二者数值的具体变化情况与该两分量本身的大小、半偏联系数表示的增量与原联系分量的比例、被迁移的原联系分量的大小有关. 可见，式(14)揭示了三元联系数系统结构中联系数分量运动变化的原因和动力，反映了物极必反的事物演变规律.

由式(15)得区域水资源承载力评价样本i的指标值联系数u′_i^[11]：

$ u_i^\prime = v_{i1}^\prime + v_{i2}^\prime I + v_{i3}^\prime J = \sum\limits_{j = 1}^{{n_k}} {\sum\limits_{k = 1}^3 {{w_j}} } v_{ijk1}^\prime + \sum\limits_{j = 1}^{{n_k}} {\sum\limits_{k = 1}^3 {{w_j}} } v_{ijk2}^\prime I + \sum\limits_{j = 1}^{{n_k}} {\sum\limits_{k = 1}^3 {{w_j}} } v_{ijk3}^\prime \mathit{J}\left( {i = 1, 2, \cdots , {\mathit{n}_i}} \right) $

(16)

式中，w_j为评价指标j的权重，由基于加速遗传算法的模糊层次分析法^[11]确定.

步骤4：采用减法集对势和三角模糊数耦合法动态确定差异度系数I. 联系数值计算的一个关键问题是如何在符合实际物理意义条件下合理确定差异度系数I. 为此，下面依据联系数减法集对势和三角模糊数理论，构造差异度系数I的三角模糊数，确定动态确定差异度系数. 在构造差异度系数I的三角模糊数过程中，如何确定差异度系数的最小取值、最可能取值和最大取值，同时这些取值随评价样本值动态变化是必须考虑的问题. 集对势作为联系数的一种伴随函数，其基本思想是如何合理地把含有确定性不确定性变化趋势信息的联系数转化为确定性的联系数值，即实现不确定性向确定性的转变，以便判别集对系统的总体发展趋势. 结合普通减法集对势^[11]和半偏减法集对势^[17]的基本思路，分别构造差异度系数I的三角模糊数，对步骤3中所得到的三元联系数u′_i=v′_i1+v′_i2I+v′_i3J有两种取法：

一是根据普通减法集对势^[11]s_f1(u)=(v′_i1－v′_i3)(1+v′_i2)=v′_i1+v′_i2(v′_i1－v′_i3)－v′_i3可构造I的三角模糊数^[9]：

$ \tilde \theta = \left( {{\theta _1}, {\theta _2}, {\theta _3}} \right) = \left( { - v_{i3}^\prime , v_{i1}^\prime - v_{i3}^\prime , v_{i1}^\prime } \right) $

(17)

若给定截集水平α(0≤α≤1)，则可将三角模糊数转化为与一定截集水平α相对应的取值区间^[9]：

$ {\tilde \theta _\alpha } = \left[ {\tilde \theta _\alpha ^L, \tilde \theta _\alpha ^R} \right] = \left[ {\left( {{\theta _2} - {\theta _1}} \right)\alpha + {\theta _1}, - \left( {{\theta _3} - {\theta _2}} \right)\alpha + {\theta _3}} \right] = \left[ {v_{i1}^\prime \alpha - v_{i3}^\prime , - v_{i3}^\prime \alpha + v_{i1}^\prime } \right] $

(18)

式中，θ₁、θ₂和θ₃分别为差异度系数I的最小取值、最可能取值和最大取值，截集水平α通常取α=0.75^[9].

二是根据半偏减法集对势^[17]${s_{f2}}(u) = v_{i1}^\prime + v_{i2}^\prime \left( {\frac{{v_{i1}^\prime }}{{v_{i1}^\prime + v_{i2}^\prime }} - \frac{{v_{i3}^\prime }}{{v_{i2}^\prime + v_{i3}^\prime }}} \right) - v_{i3}^\prime $构造I的三角模糊数^[9]：

$ \tilde \gamma = \left( {{\gamma _1}, {\gamma _2}, {\gamma _3}} \right) = \left( { - \frac{{v_{i3}^\prime }}{{v_{i2}^\prime + v_{i3}^\prime }}, \frac{{v_{i1}^\prime }}{{v_{i1}^\prime + v_{i2}^\prime }} - \frac{{v_{i3}^\prime }}{{v_{i2}^\prime + v_{i3}^\prime }}, \frac{{v_{i1}^\prime }}{{v_{i1}^\prime + v_{i2}^\prime }}} \right) $

(19)

若给定截集水平α(0≤α≤1)，则可以将三角模糊数转化为与一定截集水平α相对应的取值区间^[9]：

$ {\bar \gamma _\alpha } = \left[ {\bar \gamma _\alpha ^L, \bar \gamma _\alpha ^R} \right] = \left[ {\left( {{\gamma _2} - {\gamma _1}} \right)\alpha + {\gamma _1}, - \left( {{\gamma _3} - {\gamma _2}} \right)\alpha + {\gamma _3}} \right] = \left[ {\frac{{v_{i1}^\prime }}{{v_{i1}^\prime + v_{i2}^\prime }}\alpha - \frac{{v_{i3}^\prime }}{{v_{i2}^\prime + v_{i3}^\prime }}, - \frac{{v_{i3}^\prime }}{{v_{i2}^\prime + v_{i3}^\prime }}\alpha + \frac{{v_{i1}^\prime }}{{v_{i1}^\prime + v_{i2}^\prime }}} \right] $

(20)

式中，γ₁、γ₂、γ₃分别为差异度系数I的最小取值、最可能取值和最大取值，截集水平α通常取α=0.75^[9]. 显然，上述两种I取值方法可实现差异度系数随评价样本的变化而变化的动态取值，从而得到动态减法集对势值.

步骤5：计算评价样本i的水资源承载力等级值. 将步骤4中由式(18)和式(20)计算得到的差异度系数值(区间)分别代入式(16)可得联系数值区间，按照实数区间数的运算法则，再由联系数值与评价等级间的关系建立映射函数计算评价样本i的水资源承载力等级. 三元联系数减法集对势值s_i(u)与评价等级h_i间可构建如下转换关系^[19]：

$ {h_i} = \left\{ {\begin{array}{*{20}{l}} {2.0{{\rm{e}}^{ - 0.405{s_i}(u)}}, {s_i}(u) \le 0}\\ {2.0{{\rm{e}}^{ - 0.693{s_i}(u)}}, {s_i}(u) > 0} \end{array}} \right. $

(21)

式中，s_i(u)集对势和三角模糊法确定的联系数值区间，h_i为评价样本i的水资源承载力等级值区间.

为进一步验证上述方法的合理性和准确性，确保评价结果的可靠性，这里再采用级别特征值法^[20]计算评价样本i的水资源承载力等级. 依据步骤4中水资源承载力评价样本i的指标值联系数u′_i，运用级别特征值法^[20]计算水资源承载力等级值：

$ {H_i} = \sum\limits_{g = 1}^3 {v_{ig}^\prime } g $

(22)

式中，H_i为评价样本i的水资源承载力等级值.

步骤6：根据区域水资源承载力评价样本i的指标值联系数u′_i的减法集对势值，判别区域水资源承载力系统的状态及发展趋势. 将步骤5中计算得到的联系数减法集对势值区间两端点的平均值(期望)作为区域水资源承载力评价样本i的联系数减法集对势值s(u). 可证明，联系数减法集对势值s(u)的值域为[-1, 1]，故可根据集对势划分的“均分原则”将减法集对势值划分为5个态势^[11]，即反势s(u)∈[-1.0, -0.6)，偏反势s(u)∈[-0.6，-0.2)，均势s(u)∈[-0.2, 0.2]，偏同势s(u)∈(0.2, 0.6]，同势s(u)∈(0.6, 1.0]. 若s(u)随时间的推移，不断增加(减小)，则说明区域水资源承载力等级向好(劣)发展，其水资源承载力趋于增强(减弱).

2 实例研究

安徽省淮北市位于安徽省北部，全境界于33°16′~34°14′N，116°23′~117°02′E之间. 地处华东地区腹地，苏、豫、皖三省接壤处，是全国重要的资源型城市，也是一座新兴的现代化工业城市. 截至2020年年底，辖相山区、杜集区、烈山区和濉溪县，总面积2741 km²，户籍人口约218.8万人. 2019年，淮北市水资源总量为4.8亿m³，仅占全省水资源总量(539.87亿m³)的0.89 %，供水总量为4.22亿m³，占全省供水总量(277.72亿m³)的1.52 %. 2019年，淮北市年降雨量611.7 mm，占全省年降雨量(935.8 mm)的65.37 %. 此外，淮北市人均水资源量211.45 m³/人，占全省人均水资源量(848.07 m³/人)的24.93 %. 可见，合理准确评价淮北市水资源承载状况，可为区域水资源管理及水资源承载力预警提供科学技术支撑，有助于厘清水资源、社会经济和生态环境3大系统的内在逻辑关系，实现可持续和绿色发展.

现将基于半偏联系数和动态减法集对势耦合的区域水资源承载力评价方法应用于安徽省淮北市. 根据水资源承载力形成物理机制并参考水资源承载力评价现有研究成果，建立区域水资源承载力评价指标体系和评价等级标准，采用基于加速遗传算法的模糊层次分析法确定指标权重^[11]，见表 1.

淮北市水资源承载力评价样本数据来源于《安徽统计年鉴》(2012—2020)和《安徽省水资源公报》(2011—2019)，部分指标数据经计算得到. 结合表 1，首先将各指标数据代入式(2)~(10)可得评价样本单指标值联系数u_ijk，而此时宏观状态下的各联系数分量存在相互迁移、转化. 因此，需要考虑各联系数分量的微观运动，实现评价结果的确定性和准确性，故将式(10)各分量代入式(14)并归一化得修正后的评价样本单指标值联系数u′_ijk，考虑到篇幅有限，暂列出3个指标的单指标值联系数分量迁移变化情况，见表 2，各单指标联系数分量v′_ijkg经式(16) 加权得到评价样本指标值联系数u′_i，接着将式(18)和式(20)得到的动态差异度系数代入式(16)，可得安徽省淮北市2011—2019年水资源承载力评价样本联系数值，最后经联系数值与评价等级的转换关系式(21)计算得淮北市各年水资源承载力等级，结果见表 3、表 4.

由表 2可知：2011—2019年指标C₁的同一度分量均为0，对立度分量最大，经迁移率矩阵转化后的对立度分量减小，这与前文的证明结果一致，差异度分量增大，同一度分量仍为0，这是因为原同一度分量为0，在各分量迁移运动过程中没有同一度方向上的增量，即Δa=0. 2017年指标C₅的原联系数同异反分量为0.244、0.500、0.256，经迁移转化后为0.260、0.469、0.271，2011年指标C₆的原联系数同异反分量为0.414、0.500、0.086，转化后为0.405、0.480、0.115，可发现原始两组联系数系统结构中差异度分量均最大，经迁移转化后减小，同一度和对立度分量之和增加，可能是对立度和同一度分量二者同时增大，如2017年指标C₅，也可能是其中一个增大，另一个减小，如2011年指标C₆. 联系数分量间的微观运动结果进一步表明：经迁移转化后某个联系数分量的大小与该分量本身的大小、半偏联系数表示的增量与原联系分量的比例、被迁移的原联系分量的大小都有关.

由表 3、表 4可知：(1)从淮北市各年评价样本来看，普通减法集对势和三角模糊数法确定的差异度系数I是随评价样本的变化而变化的，如2011年评价样本差异度系数I∈[-0.258, -0.106]，2012年评价样本差异度系数I∈[-0.231, -0.081]，不同评价样本差异度系数取值不同，可见确定的差异度系数具有明显的动态特征，更符合实际情况；(2)从淮北市同一评价样本看，基于普通减法集对势和三角模糊数法确定的差异度系数I与基于半偏减法集对势和三角模糊数法确定的I值存在差异，如2019年，普通减法集对势方法得到的评价样本差异度系数为I∈[-0.226, -0.065]，而基于半偏减法集对势耦合方法得到的差异度系数I∈[-0.232, 0.003]，取值区间扩大，这说明基于半偏减法集对势耦合方法确定的差异度系数较普通减法集对势更稳妥，使得评价等级值更可靠. 为进一步说明本文构建评价方法的可靠性，亦采用级别特征值法式(22)计算淮北市2011—2019年水资源承载力等级，同时将表 3和表 4中联系数值期望作为淮北市不同年份对应的联系数值，从而判别水资源承载系统的态势，从时间尺度反映水资源承载系统的状态变化及发展态势，结果见表 5.

由表 5可知：1)基于联系数分量的级别特征值法计算得到的淮北市水资源承载力评价等级值介于2.027~2.208之间，在等级2左右浮动，处于临界超载和超载状态之间，这说明淮北市水资源承载力较差. 文献[21]报道了通过物元分析法构建水资源综合开发利用评价模型应用于淮北市的辖区相山区、杜集区、烈山区和濉溪县，结果表明相山区评价等级为3级，水资源承载力饱和即超载状态，进一步开发利用潜力小，水资源供需矛盾突出，杜集区、烈山区评价等级为2级，表明水资源开发利用规模较大，水资源利用的潜力小即处于临界超载状态. 濉溪县评价等级为1级，表明进一步开发利用水资源的潜力和态势乐观即不超载，濉溪县是淮北市面积最大的地区，工业企业少，人口集中程度小，因此对水资源的需求量小. 从整体上来说淮北市水资源承载力介于2~3级之间，即临界超载和超载状态之间，与本文研究结果基本一致，这说明本文依据偏联系数、半偏联系数等基本原理及内涵，通过引入可反映联系数系统结构中联系数分量间动态转化平衡机制的迁移率矩阵，计算评价样本联系数的方法是合理有效的.

2) 基于普通减法集对势、半偏减法集对势分别和三角模糊数耦合方法确定联系数值区间，并将联系数值区间端点的平均值作为联系数值，二者计算得到的联系数值期望十分接近，且反映的水资源承载力系统的态势基本相同，这说明在判别集对系统态势方面，两种确定差异度系数进而确定联系数值的方法均是可行的，为集对系统态势的判别提供了一种新的可靠思路. 从时间尺度上看，淮北市水资源承载力系统的态势由2011—2015年的偏反势，过渡到2016—2018年的均势，再到2019年的偏反势，整体上来说，水资源承载力有向好的发展趋势.

3) 在2011—2019年的9年中，淮北市水资源承载状态处于偏反势的次数为6次，说明淮北市水资源匮乏，存在水量短缺现象. 从评价指标看，人均水资源量、产水模数和人均供水量与该地的来水量有显著相关性，查阅安徽省统计年鉴和水资源公报可看出，受自然降雨和地形地貌等因素的影响，安徽省水资源分布具有明显的南北差异. 以2015和2019年为例，2015年淮北市(位于安徽省北部)、合肥市(位于安徽省中部)和黄山市(位于安徽省南部)人均水资源量分别为276.2、628.08和10914.21 m³/人，黄山市的人均水资源量约为合肥市的17倍，约为淮北市的39倍; 2019年淮北市、合肥市和黄山市人均水资源量分别为211.45、262.82和7532.02 m³/人，合肥市和黄山市的人均水资源量分别约为淮北市的1.24和35倍. 可见安徽省由南到北水资源分布不均匀，空间差异明显，淮北市作为安徽省北部城市，水资源禀赋较差，这与评价结果较为符合. 此外，淮北市2011—2019年人均水资源量在211.45(2019年)~583.41 m³/人(2018年)之间变化，分别约为同时期安徽省人均水资源量的24.92 % 和44.14 %，另外，在2010年9月下旬以后，安徽省淮北北部连续无有效降雨日为61~73 d，发生秋冬旱，在2011—2019这9年中，淮北市的年降雨量均未达到同期安徽省年平均降水量，其中2011、2015和2016年年降雨量分别为653.6、685.5和857.2 mm，而同期安徽省年平均降水量分别为1064.4、1362.8和1612.7 mm，所占比例分别为61.41 %、50.30 % 和53.15 %，2014年安徽省内地表水资源量淮北市最少，2015年地表水资源量较2014年继续减少，地表水资源量的减少使得更多地开采地下水资源. 文献[22]报道了淮北市是中国东部安徽省的半干旱地区，曾经是一个地下水资源丰富的地区，多年来城市人类生活用水和工农业的发展主要依靠淮北市的地下水资源. 1980s以后，随着人口的增长和工农业的发展，地下水的过度开发导致了地下水位下降(由36 m下降到-12 m)等环境和社会问题. 上述分析表明，本研究所构建模型的评价结果与实证资料吻合，从物理成因的角度验证了评价结果的合理性、稳定性和准确性，说明本文构建的区域水资源承载力评价方法具有可靠性.

为了进一步测度和比较普通减法集对势和三角模糊数法、半偏减法集对势和三角模糊数法在评价等级计算上的优劣性，分别计算上述两种方法得到的评价等级值与级别特征值法得到的评价等级值之间的相对误差，结果见表 6.

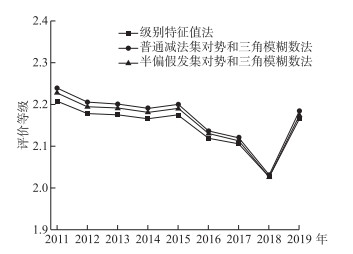
由表 6和图 1可知：(1)3种不同方法确定的淮北市水资源承载力等级值均介于2~3级之间，即处于临界超载和超载状态之间，水资源承载力较差，Cui等^[23]构建了集对分析评价模型应用于安徽省水资源承载力评价中，得到安徽省北部地区的水资源承载状态相对严峻，其中通过计算指标数联系数、指标值联系数及二者几何平均联系数并由级别特征值法得到淮北市水资源承载力等级值分别为2.33、2.30和2.32，与本文的研究结果吻合较好，相对误差5 % 左右，此外，安徽北部水资源的减少是导致其长期超载的原因. 值得注意的是，正在建设的引江济淮大型水利工程将为相对缺水的皖北地区提供可用的水资源，进一步解决水资源短缺的问题. (2)基于半偏减法集对势与三角模糊数法确定的评价等级值与级别特征值法的结果更为接近，相对误差在1 % 以内. 这说明在确定评价等级方面，采用半偏减法集对势构造三角模糊数求解差异度系数进而计算联系数值确定评价等级是优于普通减法集对势的，这与半偏减法集对势较普通减法集对势更具深刻的物理解释意义有关.

上述分析结果说明，本文所提出的修正并确定联系数方法是合理可靠的，该方法可反映联系数系统结构中联系数分量间的微观运动，将宏观状态下系统结构中的微观运动定量表达，采用基于减法集对势和三角模糊数法动态确定差异度系数更符合集对系统的实际物理过程. 因此，基于半偏联系数和动态减法集对势耦合的区域水资源承载力评价方法的评价结果更客观、准确.

3 结论

本文依据形成区域水资源承载状态的机理，构建了评价指标体系和评价等级标准，然后根据偏联系数、半偏联系数基本原理和内涵，构造了迁移率矩阵来反映联系数系统结构中联系数分量间的微观运动，从而提出了一种修正联系数分量值的方法，并基于减法集对势和三角模糊数方法动态确定了差异度系数，构建了基于半偏联系数和动态减法集对势的区域水资源承载力评价方法，将其应用于安徽省淮北市，得到以下结论：

1) 依据偏联系数、半偏联系数原理构造的迁移率矩阵，定量表示联系数系统结构中联系数分量间的微观运动，其运动结果表明原三元联系数中最大分量的值会减小，其他两个分量的变化情况与该分量本身的大小、半偏联系数表示的增量与原联系分量的比例、被迁移的原联系分量的大小有关.

2) 基于普通减法集对势法、半偏减法集对势法和级别特征值法评价结果均介于2~3级之间，说明淮北市水资源承载能力和水资源禀赋较差. 同时将评价结果与实证资料进行对比分析，进一步说明了基于半偏联系数和动态减法集对势的区域水资源承载力动态评价方法的可靠性.

3) 在判别集对系统态势方面，两种确定差异度系数进而确定联系数值的方法均是可行的，基于普通减法集对势的联系数值由2011年的-0.279变化到2018年的-0.037再到2019年的-0.218，基于半偏减法集对势的联系数值由2011年的-0.267变化到2018年的-0.035再到2019年的的-0.207，反映的态势一致，为集对系统态势的判别提供了一种新的有效思路.

4) 基于半偏减法集对势法确定的等级值与级别特征值法的结果更为接近，相对误差在1 % 以内，而基于普通减法集对势法确定的等级值与其相对误差均超过半偏减法集对势法，这说明在确定评价等级方面，采用基于半偏减法集对势法确定评价等级是优于普通减法集对势的，其原因是半偏减法集对势在差异度分量的分配上更合理，较普通减法集对势更具深刻的物理解释意义.

5) 半偏联系数是实现各联系数分量间转化的一种重要途径. 基于半偏联系数和动态减法集对势耦合的区域水资源承载力评价方法实现了区域水资源承载力定量评价，为差异度系数、联系数的准确合理确定和水资源承载力系统的动态分析及其发展趋势的判断提供了新的有效方法，是从系统结构角度出发的一种水资源复杂系统综合评价方法，属于结构水资源学的实证研究，在资源环境管理中具有重要推广应用价值.