(2: 南京信息工程大学大气环境中心, 南京 210044)
(3: 中国科学院地理科学与资源研究所生态系统网络观测与模拟重点实验室, 北京 100101)
(4: 无锡太湖学院苏格兰学院, 无锡 214063)
(2: Center on Atmospheric Environment, Nanjing University of Information Science & Technology, Nanjing 210044, P.R.China)
(3: Key Laboratory of Ecosystem Network Observation and Modeling, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, P.R.China)
(4: Scotland Academy, Wuxi Taihu University, Wuxi 214063, P.R.China)
湖泊是地球系统各圈层相互作用的联结点,是陆地水文循环的重要组成部分. 在气候系统中,湖泊代表潮湿表面,其蒸发仅受大气条件控制,是湖泊水文循环中最直接受气候变化影响的部分,是气候变化的敏锐指标[1]. 《IPCC全球升温1.5℃特别报告》指出,相较于工业化前水平,人类活动造成全球变暖大约1.0℃[2],全球变暖趋势明显,并且全球温室气体浓度仍在增加,2020年CO2、CH4、N2O浓度分别达到了工业化前水平的149%、262%、123%[3]. 气候变化改变了气温、风速、辐射强迫等与湖泊蒸发密切相关的气象因子,因此了解湖泊蒸发在全球变暖期间的变化趋势及其主控因子是必要的[4-6].
不同时间尺度的湖泊蒸发受不同的气象因子和物理过程控制. 在短时间尺度(小时到日尺度)上,湖泊蒸发主要由湖—气之间的水汽压差和风速协同控制[7-8],同时天气尺度的天气系统如冷锋过境等,会在短时间内影响湖泊蒸发量[9-10]. 在季节尺度上,月蒸发量更接近净辐射的变化趋势,但是根据湖泊的深浅不同有1~5个月的相位延迟[11-12]. 而关于气候变化背景等更长时间尺度上湖泊蒸发的主控因子研究,现有的观点主要有气候变暖、辐射控制、风速变化控制3种理论. 气候变暖理论认为,气温升高会增加大气饱和水汽压,提高大气持水能力,促进开阔水面蒸发,加速全球水分循环,形成气候变暖与水分循环的正反馈[13]. 但是在过去50年间,全球气候变暖,蒸发皿观测的蒸发量却在不断减少[14-19]. 因此,Roderick等[17]提出太阳辐射的变化(即全球变“暗”或变“亮”) 导致了蒸发皿蒸发的变化,太阳辐射是水面蒸发年际变化的主控因子. 而Johnson等认为是近50年来季风减弱造成风速减小,最终影响蒸发皿蒸发[18]. 同时另有研究表明冰期缩短会引起地表反照率变化,温度升高会引起波文比变化从而改变能量分配的比例,也可能是驱动长时间尺度蒸发变化的主要因素[20].
太湖是我国的第三大淡水湖泊,是典型的富营养化亚热带浅水湖泊,以太湖为中心的太湖流域不仅是我国重要的湿地分布区,其所在的长三角地区也是我国城市化进程最快、经济最发达的区域之一. 与深水湖泊相比,浅水湖泊对气候变化的响应更为敏锐[21]. 气象观测数据表明,近50年来,太湖流域气温、太阳辐射呈先减后增的趋势. 为获得太湖蒸发量,研究者们基于间接估算和直接观测等方法量化太湖蒸发量. 毛锐、沈行毅运用扩散法、池湖蒸发差值法[22]和修正彭曼综合法[21-23]等蒸发模型,校正岸边蒸发池数据代表太湖蒸发;随后水量平衡法[24]被用于估算太湖蒸发;随着观测手段的进步,稳定同位素方法[25-26]被用于间接反算湖面蒸发. 随着涡度相关法等直接观测方法在湖泊上的成功应用,Lee等[27]、Xiao等[28]利用涡度相关法和通量梯度法对在太湖开展了原位连续观测,积累了多年数据,Xiao等[29]基于2011—2017年的涡度相关观测数据,利用能量平衡方法进行了诊断分析,发现辐射控制着太湖蒸发的年际变化,蒸发量的增加主要是由能量输入的增加造成的,减少则是由湖表发射的向上长波辐射减少造成的.
认识更长的历史时期和气候变化情景下湖泊蒸发的变化,则需要借助模型的方法. 研究者们基于CLM4.0-LISSS和E-ε等湖泊模型[30-33]研究了太湖蒸发对气候变化的响应. Hu等[33]借助CLM4.0-LISSS模型对1979—2013年太湖蒸发进行了估算,并与蒸发皿观测反算结果进行对比,两种方法均得出太湖蒸发呈上升趋势,但由逐步回归分析得出的太湖历史蒸发的主控因子不同,蒸发皿反算结果显示气温的升高是太湖历史蒸发的主控因子,模型模拟结果为向下的短波辐射. 随后,郝晓龙等[34]在Hu等[33]的基础上利用HadCEM2-ES气候模式结果驱动CLM4.0-LISSS模型模拟了2010—2100年RCP2.6、RCP4.5及RCP8.5不同温室气体排放情景下太湖蒸发量,得出各种温室气体排放情景下太湖蒸发都呈现增加的趋势,蒸发量的增加速率与辐射强迫呈正相关,风速与水汽压差的乘积可以解释64%的潜热通量变化. 但两者采用的CLM4.0-LISSS模型中使用的粗糙度参数化方案,更适用于海上强风情况,用于太湖时潜热通量会出现异常高值[35],且模型验证时仅使用了3年的观测数据,无法表明模型可以模拟出蒸发的长期变化. 因此本文选取了2013年涡度相关观测数据与JRA-55再分析资料建立线性校正方程,通过验证2012年校正前后再分析资料与观测数据的一致性来判断校正效果,再利用校正后的JRA-55再分析资料,驱动改进了粗糙度参数化方案后的CLM4.0-LISSS模型,获得1958—2017年太湖湖面蒸发量,模拟结果与2012—2017年涡度相关观测对比验证其可用性,并分析湖面蒸发的变化趋势,寻找太湖实际蒸发年际变化的主控因子,以期为太湖地区水资源管理与气候变化研究提供科学依据.
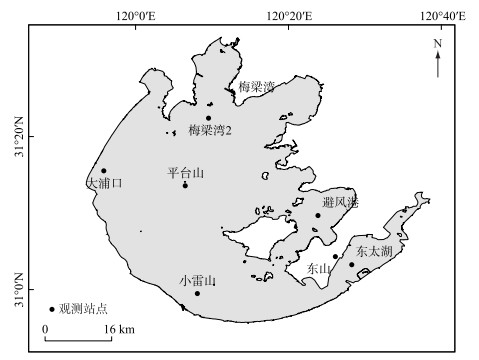
1 材料与方法 1.1 研究区域概况太湖(30°55′40″~31°32′58″N,119°52′32″~120°36′10″E,图 1),地处长江中下游,属于亚热带湿润季风气候区,多年平均气温15.97℃,年平均降水量1182 mm[33],湖表面积约为2338 km2,平均水深1.94 m,是典型的亚热带大型浅水湖泊.
|
图 1 太湖中尺度通量网观测站点位置 Fig.1 Locations of the observation sites of the Lake Taihu eddy flux network |
本文最终用于分析的太湖蒸发量数据均由观测或模拟所得潜热通量除以汽化潜热计算而来. 本研究利用2013年太湖中尺度通量网[27]避风港站(BFG,31°10′28″N,120°24′01″E)观测数据校正JRA-55再分析资料,并利用2012年的观测资料验证该再分析资料在太湖的适用性;再利用2012—2017年辐射及小气候观测资料驱动CLM4.0-LISSS模型,与观测所得的湖面蒸发量对比,验证该模型在太湖的适用性;最后利用1958—2017年JRA-55再分析数据驱动模型,获得太湖年累积蒸发量,分析太湖蒸发的长期变化趋势,寻找太湖实际蒸发年际变化的主控因子.
1.2.1 观测数据本文用于校正再分析资料、验证模型适用性的相关观测数据均来自太湖中尺度通量网[27]. 前期已有研究表明,太湖月蒸发量无空间差异[11],因此本文选择了始建于2011年12月5日、通量观测数据量较为完整且风浪区足够大的BFG站.
小气候系统架设于距湖面8.5 m处,测量空气湿度、气温(Model HMP45D/HMP155A; Vaisala, Inc, Helsinki, Finland)、风速风向(Model 03002; R. M. Young Company, Traverse City, MI, USA)及四分量辐射(Model CNR4; Kipp & Zonen B.V., Delft, the Netherlands)等气象要素. 水温梯度系统由不同深度的水温计(Model 109-L, Campbell Scientific Inc., Logan, UT, USA)构成,分别测量20、50、100、150 cm深处的水温及底泥温度.
涡度相关系统同样架设于距湖面8.5 m高度,由三维超声风速仪(CSAT3, Campbell Scientific Inc., Logan, UT, USA)、开路式红外CO2/H2O分析仪(EC150, Campbell Scientific Inc., Logan, UT, USA)组成,分别用于观测三维超声风速、大气H2O和CO2浓度,数据采样频率为10Hz;动量通量、感热通量和潜热通量数据输出步长为30 min. 通量原始数据先根据仪器工作状态和日志剔除异常值,再经过两次坐标旋转、超声虚温订正、空气密度效应订正等后处理. 对于缺失较少的通量数据(一天内少于5个数据点)进行线性内插;缺失较多的通量数据,优先使用BFG站另外一套EC数据建立线性关系插补,剩余的缺失数据,利用物质传输的相关理论插补[36].
涡度相关的观测结果存在能量平衡不闭合的问题,导致测得感热通量H、潜热通量LE偏低. 本文采用波文比(BRER)法来调整H、LE,也就是认为波文比(H/LE)的观测值是正确的,将剩余的可利用能量按波文比分配给H和LE,从而达到能量闭合. 本文的处理过程中,对3日尺度的潜热通量进行了能量闭合校正. 具体的后处理过程参见文献[11].
1.2.2 JRA-55再分析资料用于模拟太湖历史蒸发的气象数据源于日本气象厅(Japan Meteorological Agency, JMA)的第二代大气再分析产品JRA-55再分析资料[37]. JRA-55再分析资料数据自1958年开始,在JRA-25的基础上,改进了长波辐射方案,引进了四维变分技术(4D-Var)和变分偏差校正(VarBC),对平流层低层温度模拟更加精准,这对于本文的模拟非常重要. 本文使用的是1958—2017年JRA-55时间分辨率为3 h的气温、大气压、比湿、向下的长波辐射、向下的短波辐射数据,水平分辨率为1.25°×1.25°. 向上的短波辐射由向下的短波辐射乘以湖表反照率0.08获得.
再分析资料基于陆地站点发展而来,而湖陆下垫面在反照率、比热容、粗糙度等方面的不同导致了湖陆下垫面微气象条件存在差异. 因此本文采用线性回归的方法,利用2013年观测数据建立校正方程,对1958—2017年的JRA-55再分析资料进行简单的线性校正,通过对2012年校正前后数据的准确性验证校正效果.
1.2.3 蒸发量计算蒸发量E可以由观测或模拟所得潜热通量LE除以汽化潜热获得:
| $ E=\frac{L E}{\lambda} $ | (1) |
| $ \lambda=3.1475 \times 10^6-2.372 \times 10^3 T_{\mathrm{a}} $ | (2) |
式中,λ为汽化潜热,Ta为大气温度. 年累积蒸发量由3 h潜热通量转换成蒸发量后再求和计算得到.
1.3 湖泊模型介绍CLM4-LISSS模型(Community Land Model 4.0-Lake, Ice, Snow and Sediment Simulator)中的驱动数据包括气温、气压、湿度、风速、降水、净短波福射和向下的长波福射. 模型将湖体分为10层,利用大气强迫场,通过湖表薄层能量平衡经过4次迭代获得表面温度的唯一解Ts. 在每一次迭代中,摩擦速度和空气动力学阻力将重新计算,再利用公式(3)重新计算得到湖—气间感热通量H和潜热通量LE.
湖表薄层的能量平衡方程为:
| $ \beta \overrightarrow{S_{\mathrm{g}}}-\overrightarrow{L_{\mathrm{g}}}-H-L E-G=0 $ | (3) |
式中,β为保留在湖表薄层的短波辐射的比例;
| $ H =-\rho_{\mathrm{atm}} C_{\mathrm{p}} \frac{\left(\theta_{\mathrm{atm}}-T_{\mathrm{s}}\right)}{r_{\mathrm{ah}}} $ | (4) |
| $ L E =-\lambda \rho_{\mathrm{atm}} \frac{\left(q_{\mathrm{atm}}-q_{\mathrm{sat}}^{T_{\mathrm{s}}}\right)}{r_{\mathrm{aw}}} $ | (5) |
| $ G =\frac{k}{\Delta z_{\mathrm{T}} / 2}\left(T_{\mathrm{s}}-T_{\mathrm{T}}\right) $ | (6) |
式中,ρatm为湿空气密度;Cp为空气比热容;θatm为大气位温,由气温、气压计算得到[38];Ts为湖表温度;rah为大气对热量输送的阻力;λ为汽化潜热;qatm为大气比湿;qsatTs为湖表温度Ts下的饱和比湿;raw为大气对水汽输送的阻力;k为湖顶层的热导度,对于未结冰的湖泊,k包括湍流扩散系数和分子扩散系数;ΔzT和TT分别为湖表层的厚度与温度.
湖体各层温度由垂直温度扩散方程计算得到,公式为:
| $ c_{\mathrm{w}} \frac{\partial T}{\partial t}=\frac{\partial}{\partial z}\left(k \frac{\partial T}{\partial z}\right)+\frac{\mathrm{d} \phi}{\mathrm{d} z} $ | (7) |
式中,cw为深度z处的比热;T为湖体不同层的水温;k为热导度;ϕ为到达深度z处的辐射通量.
本文选择使用CLM4.0版本模拟太湖蒸发. 目前CLM模型已更新至5.0版本,但使用CLM4.0版本并不影响年尺度太湖蒸发的模拟效果. CLM5.0模拟过程中湖泊深度为可变项,即所有的物理过程(除与深度有关的混合过程除外)均可在任意深度下进行;而在CLM4.0版本中,湖泊深度则为定值. 模式中湖泊深度主要用于计算消光系数,根据Subin等[39]的敏感性分析可知,改变湖泊深度对水热通量的模拟结果与改变消光系数获得的结果类似. 而在本研究中,消光系数已通过多组敏感性实验,以年尺度上蒸发量模拟结果最佳为目标,设置为2.5 m-1,因此使用CLM4.0版本对年尺度湖面蒸发数据影响不大.
1.4 统计方法 1.4.1 Mann-Kendall趋势检验本文采用Mann-Kendall秩次相关检验(M-K)分析1958—2017年太湖蒸发量年际变化趋势[40-43]. 该方法对样本分布不作要求,且最终检验结果受异常值干扰较小,常应用于降水、蒸发、气温等随时间变化的要素的趋势变化分析. M-K趋势检验原假设H0是对于样本量为n的时间序列x,无时间变化趋势,趋势检验的统计量S定义为:
| $ S = \sum\limits_{i = 2}^n {\sum\limits_{j = 1}^{i - 1} {{\mathop{\rm sign}\nolimits} } } \left( {{x_i} - {x_j}} \right) $ | (8) |
其中,
| $ {\mathop{\rm sign}\nolimits} (\theta ) = \left\{ {\begin{array}{*{20}{l}} {1, \theta > 0}\\ {0, \theta = 0}\\ { - 1, \theta < 0} \end{array}} \right. $ | (9) |
M-K检验利用标准化后的统计量Z值判断时间序列是否有变化趋势及是否显著,变化趋势的大小用Kendall倾斜度β表示. 计算公式为:
| $ Z{\rm{ }} = \left\{ {\begin{array}{*{20}{c}} {\frac{{S + 1}}{{\sqrt {{\mathop{\rm var}} (S)} }}}&{S > 0}\\ 0&{S = 0}\\ {\frac{{S + 1}}{{\sqrt {{\mathop{\rm var}} (S)} }}}&{S < 0} \end{array}} \right. $ | (10) |
| $ \beta = {\mathop{\rm Median}\nolimits} \left[ {\frac{{{x_i} - {x_j}}}{{i - j}}} \right] $ | (11) |
式中,var(S)为统计量S的方差. 当Z值为正时,时间序列呈上升趋势;反之,时间序列呈下降趋势. |Z|大于1.28、1.96和2.32分别代表变化趋势通过了90%、95%和99%的显著性检验.
1.4.2 多元逐步回归分析各驱动变量对太湖历史蒸发的贡献率采用多元逐步回归来定量分析. 多元逐步回归方法按因变量的影响大小被依次引入回归方程中,并考察引入此因子所建立的回归方程是否显著. 当某因子的初始P值小于0.05,则此因子将被引入并重新计算P值,若重新计算的P值大于0.1,此因子将被移除. 本文利用标准化后的驱动数据和年累积蒸发量数据(变化范围0~1)建立回归方程,以此判断各气象因子对太湖蒸发的相对贡献[33, 44-46],具体如下:
| $ Y=e+a_1 x_1+a_2 x_2+\cdots a_i x_i $ | (12) |
式中,Y为标准化后的因变量,即年累积蒸发量;xi(i=1,2,…)为标准化后的因子,即各驱动变量;ai为变量xi在回归方程中的系数.
本文分析所用各驱动变量对年累积蒸发量的实际贡献率,由下列公式计算所得:
| $ \mu_i=\frac{a_i \Delta x_i}{\Delta Y} $ | (13) |
式中,Δxi和ΔY分别为xi和Y的变化量;μi为xi对Y的实际贡献率.
1.4.3 评价指标本文所用评价指标为平均偏差(mean bias error, MBE)、均方根误差(root mean square error, RMSE)、决定系数(R2)、一致性指数(I),计算公式为:
| $ MBE = \frac{1}{N}\sum\limits_{i = 1}^N {\left( {{p_i} - {o_i}} \right)} $ | (14) |
| $ RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{p_i} - {o_i}} \right)}^2}} } $ | (15) |
| $ {R^2} = 1 - \frac{{\sum\limits_i {{{\left( {{o_i} - {p_i}} \right)}^2}} }}{{\sum\limits_i {{{\left( {{o_i} - {{\bar o}_i}} \right)}^2}} }} $ | (16) |
| $ I = 1 - \frac{{\sum\limits_i {{{\left( {{o_i} - {p_i}} \right)}^2}} }}{{\sum\limits_i {{{\left( {\left| {{p_i} - {{\bar o}_i}} \right| + \left| {{o_i} - {{\bar o}_i}} \right|} \right)}^2}} }} $ | (17) |
式中,pi和oi分别为模拟值与观测值;oi为观测的平均值.
2 结果与分析 2.1 驱动数据校正结果在驱动模型模拟蒸发量之前,需利用实测资料对再分析资料进行校正,本文使用2013年BFG站点小气候及辐射观测数据对JRA-55进行简单的线性校正,再利用2012年的实测资料验证校正结果. 表 1展示了各驱动变量与实测数据的校正方程及校正前后的统计参数. 所有变量的校正方程均通过了α= 0.05的显著性检验,线性校正有效地降低了各强迫数据的系统偏差.
| 表 1 太湖地区JRA-55再分析资料驱动数据校正方程及校正前后优度统计* Tab. 1 The calibration equations of JRA-55 over Lake Taihu area and the goodness statistics |
校正前JRA-55再分析资料与BFG站点实测资料对比如图 2所示. 从相关性来看,再分析资料中向下短波辐射、长波辐射、气温、气压、比湿均与BFG观测值均呈现很好的相关性(P<0.01),平均风速与观测相关性较差(r=0.29),但仍通过了0.01的显著性检验;从一致性系数I来看,除JRA-55再分析资料的风速及气压的一致性系数较差,其余均在0.9以上;从校正前MBE及RMSE来看(如表 1所示),JRA-55再分析资料高估了太湖地区向下的短波辐射、气温,低估了向下长波辐射、气压、比湿与风速. 总体而言,JRA-55中的再分析资料中向下长波辐射、向下短波辐射、气温、比湿与实测值偏差较小,但气压存在明显的系统偏差,风速信号接近陆地观测,与湖泊风速有很大差异.

|
图 2 2012年校正前JRA-55再分析资料与BFG站点实测资料的对比:(a)向下短波辐射;(b)向下长波辐射;(c)气温;(d)比湿;(e)风速;(f)气压 Fig.2 Comparison between JRA-55 reanalysis data without calibration and observation at the BFG site in 2012: (a) downward short-wave radiation; (b) downward long-wave radiation; (c) air temperature; (d) specific humidity; (e) wind speed; (f) air pressure |
校正后,向下短波、向下长波辐射的MBE分别由23.76和-16.74 W/m2下降至-3.10和-1.08 W/m2;气温由被高估0.030℃校正至MBE仅有0.004℃;比湿的平均偏差由-0.76 g/kg降至-0.15 g/kg;气压被低估的现象明显改善,校正后MBE仅有0.26 hPa;风速被低估的现象也得到明显改善,MBE由-2.66 m/s降低至0.14 m/s. 总体而言,线性校正方法有效地校正了JRA-55再分析资料与湖上观测数据的系统偏差.
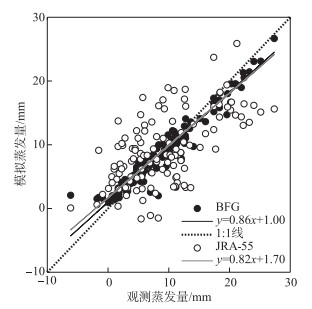
2.2 CLM4.0-LISSS模型及再分析资料适用性验证图 3展示了2012年BFG观测蒸发量与CLM4.0-LISSS模拟蒸发量的对比结果,用于验证模型的适用性. 模型能很好地模拟出2012年蒸发量的逐日变化和季节变化趋势. 春季,模拟及观测蒸发量均迅速增加,6月因“梅雨”季太阳辐射的减少而稍有减少,7、8月达到最大值,随后蒸发量逐渐减小,并于冬季达到最小值. 图 4也表明,观测与模拟值的变化范围相一致,3日平均的模拟值与观测值建立的线性回归线斜率等于0.86,MBE和RMSE分别为-0.3和2.0 mm. 这证明了CLM4.0-LISSS模型有模拟太湖蒸发的能力,可用于太湖历史蒸发量变化趋势分析研究.

|
图 3 2012年3日累积蒸发量时间序列 (黑色实线代表BFG站点EC观测值所得蒸发量(经能量平衡闭合校正)) Fig.3 Time series of 3-day accumulated lake evaporation in 2012 (Black line represents evaporation calculated by EC observation at BFG (forcing energy balance closure at 3-daily timescale)) |
|
图 4 模拟与观测的3日累积蒸发量的1 ∶1图 (●代表BFG在线观测驱动模型;○代表再分析资料驱动模型) Fig.4 Comparison between simulation and observation (●, simulation forced by in situ observation; ○, simulation forced by calibrated JRA-55) |
校正后的JRA-55再分析资料被用于驱动模型,以验证再分析资料的适用性. 图 4可以看出,相比于使用小气候系统观测数据驱动模型,利用再分析资料驱动模型时,模型表现略有下降,虽然两者拟合线接近,但模拟值更加离散(MBE=0.1 mm,RMSE=5.5 mm). 模型虽然能很好地模拟出太湖蒸发的季节变化趋势(图 3),但在秋冬季节,模型模拟值明显偏高,春夏季节蒸发量的模拟值偏低,这可能与每年只取了一个校正系数有关. 但是,季节性偏差在年尺度上相互抵消,年累积蒸发量的模拟值与观测值相近,因此本文没有再分季节/分月对再分析资料进行校正. 2012—2017年太湖年累积蒸发量的模拟值(观测值)分别为1050.3 mm(1007.0 mm)、1113.1 mm(1129.0 mm)、1005.1 mm(1011.9 mm)、977.5 mm(1036.3 mm)、983.9 mm(1079.5 mm)、1081.7 mm(1123.8 mm),观测值和模式值的对比也表明再分析资料能模拟出太湖年累计蒸发量的趋势变化(图 5). 因此本文认为校正后的JRA-55再分析资料可以驱动模型模拟年际尺度的湖泊蒸发.

|
图 5 1958—2017年太湖蒸发量模拟值的年际变化(黑色实线代表模型模拟年累积蒸发量;灰色虚线代表1958—2017蒸发量趋势拟合线;蓝色虚线代表1958—1977年蒸发量线性回归线;红色虚线代表1978—2017年蒸发量线性回归线;○代表2012—2017年观测年累计蒸发量) Fig.5 Trends of simulated annual lake evaporation over Lake Taihu from 1958 to 2017 (Black solid line represents annual lake evaporation simulated by CLM-LISSS forced by JRA-55; grey dotted line represents linear fitting line for JRA-55 data from 1958 to 2017; blue dotted line represents linear fitting line for JRA-55 data from 1958 to 1977; red dotted line represents linear fitting line for JRA-55 data from 1978 to 2017;○, observed accumulated lake evaporation from 2012 to 2017) |
1958—2017年太湖年累积蒸发量模拟值的时间序列如图 5所示. 近60年来,太湖年累积蒸发量的平均值为1018.2 mm,其中1958—1962、1965—1966、1968—1970、1972—1977、1980—1990、1999、2002、2014—2016年共31年蒸发量小于平均值,最小值出现于1977年,为870.6 mm,其余年份蒸发量高于60年平均值,最大值出现于2004年,为1120.2 mm. 需要注意的是,1977年累积蒸发量较多年平均值异常偏低约14.49%,这可能是由于1977年6月降水量较多,太阳辐射偏低(125.28 W/m2,远低于平均值155.76 W/m2),导致1977年全年太阳辐射仅有128.65 W/m2,远低于平均水平(136.99 W/m2)约6.09%,且1977年大气比湿较高(10.7 g/kg),比平均值(10.3 g/kg)高约6.8%,而敏感性分析结果表明潜热通量对太阳辐射及比湿极其敏感,将1977年太阳辐射增加6%,比湿减少6%后,蒸发量模拟值将增加至1022.4 mm,与多年均值相近.
线性回归和M-K趋势检验被用于分析蒸发量的变化趋势分析. 线性回归分析说明,1958—2017年,太湖蒸发量整体以1.4 mm/a的速率波动上升. M-K趋势检验也显示太湖蒸发量整体呈上升趋势,上升速率为1.4 mm/a,并通过了99%的显著性检验(Z=3.30). 但是在此期间太湖蒸发量明显被分为两个阶段:1958—1977年间,太湖蒸发量呈现了明显的下降趋势(线性回归斜率=-4.0 mm/a,Kendall倾斜度=-3.6 mm/a,Z=-1.89,通过了90%的显著性检验);1978—2017年间,M-K趋势检验显示,太湖蒸发量以2.3 mm/a的速度增加(Z=2.69,通过了99%的显著性检验). 总体而言,1958—2017年间太湖蒸发量以1977年为界限,呈现先减后增的趋势.
本研究计算所得太湖蒸发量在1978—2017年间以2.3 mm/a的速度增加,这与Hu等[33]利用MERRA再分析资料驱动湖模式计算得到1979—2013年间太湖蒸发量以2.96 mm/a的速率增加,以及蒸发皿蒸发量观测值以2.54 mm/a的速率增加的结论较为一致. Rong等[45]结合Penman-Monteith方程与参考蒸散率计算了2003—2010年间距离太湖640 km的另一浅水湖泊东平湖的蒸发,其蒸发量也呈上升趋势,上升速率为4.55 mm/a. 而与太湖同纬度的青藏高原湖泊色林措蒸发量也在2007—2015年间以4.3 mm/a的速度增加[43].
2.4 驱动数据的年际变化趋势分析1958—2017年气温(Ta)、气压(Pa)、比湿(qa)、风速(U)、向下长波辐射(L↓)、净短波辐射(S*)等强迫数据的变化趋势如图 6(线性回归方法)和表 2所示(M-K趋势检验法). 总体来说,1958—2017年间,Ta的增加趋势最为显著,线性回归趋势线斜率为0.015℃/a(P<0.01),M-K趋势检验显示气温平均每年升高0.014℃,统计量Z值为3.50,通过了置信水平为99%的显著性检验. 气温最低值(15.82℃)出现于1984年,最高值(17.79℃)出现于1998年. L↓在1958—2017年也呈现显著增加的趋势,M-K方法计算得到的L↓增加量为0.053 W/(m2 ·a)(置信水平为95%),线性回归计算得到的L↓增长速率为0.048 W/(m2 ·a)(P<0.05). M-K方法显示S↓以每年0.047 W/m2的趋势波动上升(置信水平为90%),但线性回归结果未通过趋势检验. S↓变量范围为128.24~143.86 W/m2,其中1977年达到最小值,2007年达到最大值. 研究表明,中国的地面太阳辐射大致以1990年为界,呈现先减少后增多的趋势[47],这与本文研究结果基本相符合. 其他变量(qa、U、Pa)在1958—2017年间无显著变化趋势. 本研究校正后的JRA-55再分析资料的风速在1958—2017年间无显著下降趋势,这与Hu等[33]使用的MERRA再分析资料得到的结论相同,但与地面观测所得到的结论存在差异. 近50年来,地表粗糙度的增加(如城市发展、植被增加、耕地变化等)造成了内陆近地面风速持续减弱,观测中海洋和沿海地区的近地层风速大多呈现出上升趋势[48-49]. 这可能是因为JRA-55再分析资料未考虑粗糙度的变化,且同化时使用的地表观测资料与ERA-40一致,仅使用了温度、湿度、降雪资料[50-51],未包含土地利用变化(如城市化进程等)信息,所以再分析资料中的近地层风速变化趋势弱于气象站观测数据[51]. 但是由于本文研究站点位于湖上,地表粗糙度小且变化不大,因此校正后的再分析资料因未考虑地表粗糙度变化而呈现出不显著变化趋势不影响本研究使用其作为驱动数据.

|
图 6 1958—2017年JRA-55资料气象因子变化趋势(黑色实线代表年平均值;灰色虚线代表1958—2017年间各气象因子线性回归拟合线;蓝色虚线代表1958—1977年间各气象因子线性回归拟合线;红色虚线代表1978—2017年间各气象因子线性回归拟合线) Fig.6 Trends of meteorological variables of JRA-55 from 1958 to 2017 (Black lines represent annual mean meteorological variables; grey dotted lines represent linear regression lines for JRA-55 annual mean meteorological variables from 1958 to 2017; blue dotted lines represent linear regression lines for JRA-55 annual mean meteorological variables from 1958 to 1977; red dotted lines represent linear regression lines for JRA-55 annual mean meteorological variables from 1978 to 2017) |
| 表 2 1958—2017年间年均气温、气压、比湿、风速、向下长波辐射、向下短波辐射M-K检验Z值及变化速率 Tab. 2 Z values and change rates of the M-K trend tests for annual mean air temperature, air pressure, specific humidity, wind speed, downward longwave radiation and downward solar radiation from 1958 to 2017 |
驱动变量的变化趋势也被分为1958—1977年及1978—2017年两个阶段分析(表 2). M-K方法显示1958—1977年间,除L↓无明显年际变化趋势外,Ta、qa、U和S↓均表现出明显的下降趋势,Pa呈显著的增加趋势;线性回归方法显示除气温以0.047℃/a的趋势下降外,其余驱动变量无显著变化特征. 1978—2017年间,各气象因子的年际变化趋势与1958—1977年存在差异. Ta、qa、S↓由显著下降趋势转变为显著上升(M-K趋势检验方法),上升趋势分别为0.032℃/a(Z=4.46,通过了99%的显著性检验)、7.05×10-3 kg/kg(Z=2.11,通过了95%的显著性检验)和0.10 W/(m2 ·a)(Z=-1.40,通过了90%的显著性检验). U和L↓则转变为呈明显的上升趋势,1977年后分别以9.69×10-4 m/(s ·a)、0.094 W/(m2 ·a)的速度增长,并分别通过了90%、99%的显著性检验. Pa则呈现了明显的下降趋势. 总体来说,气象因子和辐射能量在1958—1977年间与1978—2017年间呈现了不同的趋势,这对于解释蒸发量的年际变化有重要意义.
2.5 太湖蒸发年际变化主控因子分析为确定太湖蒸发量年际变化主控因子,我们利用多元逐步回归分析了各要素对蒸发量的实际贡献率. 基于前文趋势分析结果,将研究时段分为1958—1977年和1978—2017年两个时间段分别探讨. 1958—1977年间太湖蒸发与气象因子之间的多元回归方程为E=-0.28qa+0.43L↓+0.71S↓. Ta、Pa、U被排除在方程外,仅保留了qa、L↓、S↓ 3个变量. 方程的R2为0.764,说明方程是可以解释76.4%太湖蒸发量的变异. 根据公式(13)计算可得,S↓对太湖蒸发变化的贡献比率最大,高达63.51%,其次来自于L↓的贡献(38.10%),另外qa的实际贡献为-24.48%,位列第三,而Ta、Pa和U对太湖蒸发年际变化贡献很小;由1978—2017年数据建立的回归方程与1958—1977年有所不同,Pa、U、L↓被移出方程,保留了Ta、qa、S↓ 3个变量,回归方程为E=0.42Ta-0.31qa+0.51S↓,对太湖蒸发年际变化贡献较大的因素为Ta、qa、S↓,三者的实际贡献率分别为44.54%、-39.13%、52.51%;与此同时,1958—2017年的全部数据也被用于建立多元逐步回归方程,Ta、qa、L↓、S*的多元逐步回归系数分别为0.37、-0.39、0.17、0.55. Pa、U被排除在回归方程外. 方程的R2为0.851,说明方程可以解释的湖泊蒸发量的变异率为85.1%. 从贡献率来看,辐射是湖泊蒸发的直接能量来源,S*的增加(贡献率为54.94%)是1958—1977年太湖年累积蒸发量增加的主要原因. 第二大贡献来自qa,qa抵消了部分由辐射减少带来的正面贡献,占43.49%. Ta、L↓的贡献分别为39.59%和18.03%. 这个结果与分段建立方程的结果相吻合. 总得来说,S↓的增加是造成太湖1958—2017年蒸发量增加的主控因子,L↓、Ta、qa也会影响湖泊蒸发年际变化.
3 讨论目前,关于控制开阔水面蒸发年际变化的主要气象因子有辐射控制、温度、风速变化3种观点. 大部分研究采用蒸发皿测算量代替(蒸发皿观测乘以系数或将其置于湖上)实际水面蒸发,或利用Penman公式及其衍生公式估算,得出蒸发量与同期气温(平均气温/最低气温/气温日较差)相关性最大[18, 33, 52-58],但有研究认为蒸发皿蒸发量变化与气温关系不大,因为早有观测证明北半球冬季的总蒸发量大于夏季[59],且部分地区气温与蒸发量变化呈相反趋势,即存在“蒸发悖论”现象,并用近50年来季风减弱造成风速减小[18-19, 46, 60-66],或云层覆盖和气溶胶浓度增加造成太阳辐射(或日照时数)减少[17-19, 63, 67-70]来解释. 也有研究认为蒸发皿蒸发量只是陆地蒸发量增加的信号(陆地蒸发量使得蒸发皿周围湿度梯度降低,造成蒸发皿蒸发量下降),只有在周围陆表环境水分供应充足时才可以代表开阔水面蒸发[16]. 近年来,涡度相关方法被用于观测开阔水面蒸发,并逐步发展成为国际通用的通量观测标准方法,结合各类模型模拟过去或未来气候情景下的水面蒸发用于分析蒸发量的年际变化. 对于高纬度结冰水体,大部分研究认为全球变暖导致湖泊冰期缩短,进而引发的反照率变化,是影响水面蒸发年际变化的重要因素[20, 71-73]. 一部分研究利用未来气候情景的气象数据模拟蒸发时发现,当辐射输入无明显变化时蒸发量仍存在明显年际变化,因此气温加速了湖泊蒸发年际变化,且由于湖泊表面增温速度慢于空气增温速度,因此波文比发生改变,能量更多分配用于蒸发(即潜热),造成蒸发逐年增加[20, 72, 74-75]. 但对于未结冰的湖泊,在不同未来气候情景下,辐射强迫存在差异,蒸发量的增加速率也会随着辐射强迫的增加而增大[34]. 大部分研究通过长年EC观测或湖模式、蒸发模式的敏感性分析、相关性分析等方法得出辐射是开阔水域蒸发的能量来源,其变化是蒸发年际变化的主控因子,辐射变化对蒸发趋势的贡献大于气温变化的贡献[1, 29, 33, 68, 76-78],与本文的结果一致.
4 结论本研究利用2013年BFG观测数据校正了JRA-55再分析资料并驱动CLM4.0-LISSS模型,模拟了太湖1958—2017年间湖面蒸发量,利用2012年模拟所得蒸发量与避风港站点实测数据验证模型与再分析资料的适用性,利用M-K趋势检验分析了长时间尺度上太湖蒸发量的变化趋势,再利用多元逐步回归方法寻找太湖实际蒸发的年际变化的主控因子. 主要研究成果如下:
1) 利用校正后的JRA-55再分析资料驱动模型时,蒸发的模拟存在季节偏差,但季节性偏差在年尺度上相互抵消,2012年(2013年)年累积蒸发量的模拟值与观测值相近,分别为1050.3 mm(1113.1 mm)和1007.0 mm(1129.0 mm). JRA-55再分析资料可用于年际湖泊蒸发的模拟.
2) 1958—2017年太湖蒸发分为两个阶段:1958—1977年间,蒸发呈现了明显的下降趋势,下降速率为-3.6 mm/a;1978—2017年间,太湖蒸发量以2.3 mm/a的速度增加.
3) 通过多元逐步回归分析可知,向下的短波辐射是太湖1958—2017年间年尺度蒸发的主控因子,向下的长波辐射、气温、比湿也会影响湖泊蒸发年际变化,蒸发量对风速变化和气压变化不敏感.
| [1] |
Lenters JD, Kratz TK, Bowser CJ. Effects of climate variability on lake evaporation: Results from a long-term energy budget study of Sparkling Lake, northern Wisconsin (USA). Journal of Hydrology, 2005, 308(1/2/3/4): 168-195. DOI:10.1016/j.jhydrol.2004.10.028 |
| [2] |
IPCC. Special report on global warming of 1.5℃. Cambridge: Cambridge University Press, 2018.
|
| [3] |
WMO ed. The greenhouse gas bulletin. Geneva: World Meteorological Organization, 2021.
|
| [4] |
Fu GB, Liu CM, Chen SL et al. Investigating the conversion coefficients for free water surface evaporation of different evaporation Pans. Hydrological Processes, 2004, 18(12): 2247-2262. DOI:10.1002/hyp.5526 |
| [5] |
Sun L, Wu GX. Influence of land evapotranspiration on climate variations. Science in China Series D: Earth Sciences, 2001, 44(9): 838-846. DOI:10.1007/BF02907096 |
| [6] |
Zhang YQ, Leuning R, Chiew FHS et al. Decadal trends in evaporation from global energy and water balances. Journal of Hydrometeorology, 2012, 13(1): 379-391. DOI:10.1175/jhm-d-11-012.1 |
| [7] |
Blanken PD, Rouse WR, Culf AD et al. Eddy covariance measurements of evaporation from Great Slave Lake, Northwest Territories, Canada. Water Resources Research, 2000, 36(4): 1069-1077. DOI:10.1029/1999WR900338 |
| [8] |
Wang BB, Ma YM, Ma WQ et al. Physical controls on half-hourly, daily, and monthly turbulent flux and energy budget over a high-altitude small lake on the Tibetan Plateau. Journal of Geophysical Research: Atmospheres, 2017, 122(4): 2289-2303. DOI:10.1002/2016JD026109 |
| [9] |
Liu HP, Zhang Y, Liu SH et al. Eddy covariance measurements of surface energy budget and evaporation in a cool season over southern open water in Mississippi. Journal of Geophysical Research: Atmospheres, 2009, 114(D4): D04110. DOI:10.1029/2008JD010891 |
| [10] |
Liu HP, Blanken PD, Weidinger T et al. Variability in cold front activities modulating cool-season evaporation from a southern inland water in the USA. Environmental Research Letters, 2011, 6(2): 024022. DOI:10.1088/1748-9326/6/2/024022 |
| [11] |
Wang W, Xiao W, Cao C et al. Temporal and spatial variations in radiation and energy balance across a large freshwater lake in China. Journal of Hydrology, 2014, 511: 811-824. DOI:10.1016/j.jhydrol.2014.02.012 |
| [12] |
Blanken PD, Spence C, Hedstrom N et al. Evaporation from Lake Superior: 1. Physical controls and processes. Journal of Great Lakes Research, 2011, 37(4): 707-716. DOI:10.1016/j.jglr.2011.08.009 |
| [13] |
Engeland K, Skaugen TE, Haugen JE et al. Comparison of evaporation estimated by the HIRHAM and GWB models for present climate and climate change scenarios. Norwegian Meteorological Institute, 2004.
|
| [14] |
Peterson TC, Golubev VS, Ya GP. Evaporation losing its strength. Nature, 1995, 377(6551): 687-688. |
| [15] |
Chattopadhyay N, Hulme M. Evaporation and potential evapotranspiration in India under conditions of recent and future climate change. Agricultural and Forest Meteorology, 1997, 87(1): 55-73. DOI:10.1016/S0168-1923(97)00006-3 |
| [16] |
Brutsaert W, Parlange MB. Hydrologic cycle explains the evaporation paradox. Nature, 1998, 396(6706): 30. DOI:10.1038/23845 |
| [17] |
Roderick ML, Farquhar GD. The cause of decreased pan evaporation over the past 50 years. Science, 2002, 298(5597): 1410-1411. DOI:10.1126/science.1075390 |
| [18] |
Johnson F, Sharma A. A comparison of Australian open water body evaporation trends for current and future climates estimated from class A evaporation Pans and general circulation models. Journal of Hydrometeorology, 2010, 11(1): 105-121. DOI:10.1175/2009jhm1158.1 |
| [19] |
Cong ZT, Yang DW, Ni GH. Does evaporation paradox exist in China?. Hydrology and Earth System Sciences, 2009, 13(3): 357-366. DOI:10.5194/hess-13-357-2009 |
| [20] |
Wang W, Lee XH, Xiao W et al. Global lake evaporation accelerated by changes in surface energy allocation in a warmer climate. Nature Geoscience, 2018, 11(6): 410-414. DOI:10.1038/s41561-018-0114-8 |
| [21] |
Shen HY. Climatological calculation of surface evaporation in Taihu Lake. Journal of China Hydrology, 1984, 4(4): 12-18. [沈行毅. 太湖水面蒸发量的气候学计算. 水文, 1984, 4(4): 12-18.] |
| [22] |
Mao R. Preliminary experimental study of evaporation from water surface of Lake Tai and Lake Tuangui, Jiangsu Province. Oceanologia et Limnologia Sinica, 1978, 9(1): 26-35. [毛锐. 太湖、团氿湖水面蒸发的初步研究. 海洋与湖沼, 1978, 9(1): 26-35.] |
| [23] |
Mao R. Forecasting model of evaporation from Taihu Lake and its application. J Lake Sci, 1992, 4(4): 8-13. [毛锐. 太湖水面蒸发量预报模型及其应用. 湖泊科学, 1992, 4(4): 8-13. DOI:10.18307/1992.0402] |
| [24] |
Qin BQ, Xu PZ, Wu QL et al. Environmental issues of Lake Taihu, China. Hydrobiologia, 2007, 581(1): 3-14. DOI:10.1007/s10750-006-0521-5 |
| [25] |
Xiao W, Fu Jr, Wang W et al. Estimating evaporation over a large and shallow lake using stable isotopic method: A case study of Lake Taihu. J Lake Sci, 2017, 29(4): 1009-1017. [肖薇, 符靖茹, 王伟等. 用稳定同位素方法估算大型浅水湖泊蒸发量——以太湖为例. 湖泊科学, 2017, 29(4): 1009-1017. DOI:10.18307/2017.0425] |
| [26] |
Xie CY, Xiao W, Xu JZ et al. Comparison of using hydrogen and oxygen isotopes in tracing water evaporation in Taihu Lake. Oceanologia et Limnologia Sinica, 2019, 50(1): 74-85. [谢成玉, 肖薇, 徐敬争等. 氢和氧稳定同位素示踪湖泊蒸发的对比研究. 海洋与湖沼, 2019, 50(1): 74-85. DOI:10.11693/hyhz20180300064] |
| [27] |
Lee XH, Liu SD, Xiao W et al. The Taihu eddy flux network: An observational program on energy, water, and greenhouse gas fluxes of a large freshwater lake. Bulletin of the American Meteorological Society, 2014, 95(10): 1583-1594. DOI:10.1175/bams-d-13-00136.1 |
| [28] |
Xiao W, Liu SD, Li HC et al. A flux-gradient system for simultaneous measurement of the CH4, CO2, and H2O fluxes at a lake-air interface. Environmental Science & Technology, 2014, 48(24): 14490-14498. DOI:10.1021/es5033713 |
| [29] |
Xiao W, Zhang Z, Wang W et al. Radiation controls the interannual variability of evaporation of a subtropical lake. Journal of Geophysical Research: Atmospheres, 2020, 125(8): e2019JD031264. DOI:10.1029/2019JD031264 |
| [30] |
Gao YQ. Variability of evaporation from Lake Taihu and its response to climate change[Dissertation]. Nanjing: Nanjing University of Information Science & Technology, 2017. [高雅琦. 太湖蒸发量的变化特征及其对气候变化响应的研究[学位论文]. 南京: 南京信息工程大学, 2017. ]
|
| [31] |
Cheng X, Wang YW, Hu C et al. The lake-air exchange simulation of a lake model over eastern Taihu Lake based on the E-ε turbulent kinetic energy closure thermodynamic process. Acta Meteorologica Sinica, 2016, 74(4): 633-645. [程昕, 王咏薇, 胡诚等. 应用E-ε湍流动能闭合湖泊热力学过程模型对东太湖湖-气交换的模拟. 气象学报, 2016, 74(4): 633-645. DOI:10.11676/qxxb2016.043] |
| [32] |
Deng B, Liu SD, Xiao W et al. Evaluation of the CLM4 lake model at a large and shallow freshwater lake. Journal of Hydrometeorology, 2013, 14(2): 636-649. DOI:10.1175/jhm-d-12-067.1 |
| [33] |
Hu C, Wang YW, Wang W et al. Trends in evaporation of a large subtropical lake. Theoretical and Applied Climatology, 2017, 129(1/2): 159-170. DOI:10.1007/s00704-016-1768-z |
| [34] |
Hao XL, Wang YW, Gao YQ et al. Preliminary simulation analysis of the response of Lake Taihu evaporation to future climate change. Journal of the Meteorological Sciences, 2020, 40(4): 505-512. [郝晓龙, 王咏薇, 高雅琦等. 太湖蒸发量对未来气候变化响应的初步模拟分析. 气象科学, 2020, 40(4): 505-512. DOI:10.3969/2019jms.0014] |
| [35] |
Jing SJ, Xiao W, Wang W et al. Evaluation on the performance of CLM4-LISSS in simulating water and heat fluxes at multiple time scales over Lake Taihu. J Lake Sci, 2019, 31(6): 1698-1712. [荆思佳, 肖薇, 王伟等. CLM4-LISSS模型对太湖多时间尺度水热通量模拟性能的评估. 湖泊科学, 2019, 31(6): 1698-1712. DOI:10.18307/2019.0611] |
| [36] |
Xiao W, Liu SD, Li XH et al. Transfer coefficients of momentum, heat and water vapour in the atmospheric surface layer of a large shallow freshwater lake: A case study of Lake Taihu. J Lake Sci, 2012, 24(6): 932-942. [肖薇, 刘寿东, 李旭辉等. 大型浅水湖泊与大气之间的动量和水热交换系数——以太湖为例. 湖泊科学, 2012, 24(6): 932-942. DOI:10.18307/2012.0617] |
| [37] |
Kobayashi S, Ota Y, Harada Y et al. The JRA-55 reanalysis: General specifications and basic characteristics. Journal of the Meteorological Society of Japan Ser II, 2015, 93(1): 5-48. DOI:10.2151/jmsj.2015-001 |
| [38] |
Stull RB ed. An introduction to boundary layer meteorology. Dordrecht: Kluwer Academic Publishers, 1988.
|
| [39] |
Subin ZM, Riley WJ, Mironov D. An improved lake model for climate simulations: Model structure, evaluation, and sensitivity analyses in CESM1. Journal of Advances in Modeling Earth Systems, 2012, 4(1): 183-204. |
| [40] |
Mann HB. Nonparametric tests against trend. Econometrica, 1945, 13(3): 245. DOI:10.2307/1907187 |
| [41] |
Kendall MG. Rank correlation methods. British Journal of Psychology, 1990, 25(1): 86-91. |
| [42] |
Partal T, Kahya E. Trend analysis in Turkish precipitation data. Hydrological Processes, 2006, 20(9): 2011-2026. DOI:10.1002/hyp.5993 |
| [43] |
Guo YH, Zhang YS, Ma N et al. Long-term changes in evaporation over Siling Co Lake on the Tibetan Plateau and its impact on recent rapid lake expansion. Atmospheric Research, 2019, 216: 141-150. DOI:10.1016/j.atmosres.2018.10.006 |
| [44] |
Xu CY, Gong LB, Jiang T et al. Analysis of spatial distribution and temporal trend of reference evapotranspiration and pan evaporation in Changjiang (Yangtze River) catchment. Journal of Hydrology, 2006, 327(1/2): 81-93. DOI:10.1016/j.jhydrol.2005.11.029 |
| [45] |
Rong Y, Su HB, Zhang RH et al. Effects of climate variability on evaporation in Dongping Lake, China, during 2003-2010. Advances in Meteorology, 2013, 2013: 789290. DOI:10.1155/2013/789290 |
| [46] |
Wang Y, Jiang T, Bothe O et al. Changes of pan evaporation and reference evapotranspiration in the Yangtze River Basin. Theoretical and Applied Climatology, 2007, 90(1/2): 13-23. DOI:10.1007/s00704-006-0276-y |
| [47] |
Qi Y, Fang SB, Zhou WZ. Variation and spatial distribution of surface solar radiation in China over recent 50 years. Chinese Journal of Plant Ecology, 2014, 34(24): 7444-7453. [齐月, 房世波, 周文佐. 近50年来中国地面太阳辐射变化及其空间分布. 生态学报, 2014, 34(24): 7444-7453. DOI:10.5846/stxb201303130409] |
| [48] |
Troccoli A, Muller K, Coppin P et al. Long-term wind speed trends over Australia. Journal of Climate, 2012, 25(1): 170-183. DOI:10.1175/2011jcli4198.1 |
| [49] |
Turner J, Colwell SR, Marshall GJ et al. Antarctic climate change during the last 50 years. International Journal of Climatology, 2005, 25(3): 279-294. DOI:10.1002/joc.1130 |
| [50] |
Lim YK, Cai M, Kalnay E et al. Observational evidence of sensitivity of surface climate changes to land types and urbanization. Geophysical Research Letters, 2005, 32(22): L22712. DOI:10.1029/2005GL024267 |
| [51] |
Wu J, Zha JL, Zhao DM. Evaluating the effects of land use and cover change on the decrease of surface wind speed over China in recent 30years using a statistical downscaling method. Climate Dynamics, 2017, 48(1/2): 131-149. DOI:10.1007/s00382-016-3065-z |
| [52] |
Qin B, Huang Q. Evaluation of the climatic change impacts on the inland lake—A case study of Lake Qinghai, China. Climatic Change, 1998, 39: 695-714. DOI:10.1023/A%3A1005319616456 |
| [53] |
Gao B, Fan JZ, Jing YG et al. Changing trend of pan evaporation and its cause over the past 33 years in the Weihe watershed. Journal of Chengdu University of Information Technology, 2012, 27(1): 77-82. [高蓓, 范建忠, 景毅刚等. 近33年来渭河流域蒸发皿蒸发量的变化特征及原因分析. 成都信息工程学院学报, 2012, 27(1): 77-82.] |
| [54] |
Han PF, Wang XS, Hu XN et al. Dynamic relationship between lake surface evaporation and meteorological factors in the Badain Jaran Desert. Arid Zone Research, 2018, 35(5): 1012-1020. [韩鹏飞, 王旭升, 胡晓农等. 巴丹吉林沙漠湖泊水面蒸发与气象要素的动态关系. 干旱区研究, 2018, 35(5): 1012-1020. DOI:10.13866/j.azr.2018.05.02] |
| [55] |
Soroush F, Fathian F, Khabisi FSH et al. Trends in pan evaporation and climate variables in Iran. Theoretical and Applied Climatology, 2020, 142(1/2): 407-432. DOI:10.1007/s00704-020-03262-9 |
| [56] |
Jerin JN, Islam HMT, Islam ARMT et al. Spatiotemporal trends in reference evapotranspiration and its driving factors in Bangladesh. Theoretical and Applied Climatology, 2021, 144(1/2): 793-808. DOI:10.1007/s00704-021-03566-4 |
| [57] |
Huang JT, Li ZZ, Wang WK et al. Characteristics of evaporation and its effect factors in the Golmud River catchment. Hydrogeology & Engineering Geology, 2021, 48(3): 31-37. [黄金廷, 李宗泽, 王文科等. 格尔木河流域水面蒸发特征及影响因素分析. 水文地质工程地质, 2021, 48(3): 31-37.] |
| [58] |
Pour SH, Wahab AKA, Shahid S et al. Changes in reference evapotranspiration and its driving factors in peninsular Malaysia. Atmospheric Research, 2020, 246: 105096. DOI:10.1016/j.atmosres.2020.105096 |
| [59] |
Ohmura A, Wild M. Climate change is the hydrological cycleaccelerating?. Science, 2002, 298(5597): 1345-1346. DOI:10.1126/science.1078972 |
| [60] |
Gao G, Chen DL, Ren GY et al. Spatial and temporal variations and controlling factors of potential evapotranspiration in China: 1956-2000. Journal of Geographical Sciences, 2006, 16(1): 3-12. DOI:10.1007/s11442-006-0101-7 |
| [61] |
Xu CY, Gong LB, Jiang T et al. Decreasing reference evapotranspiration in a warming climate—A case of Changjiang (Yangtze) River catchment during 1970-2000. Advances in Atmospheric Sciences, 2006, 23(4): 513-520. DOI:10.1007/s00376-006-0513-4 |
| [62] |
Jun G. Change in pan evaporation and the influential factors over China: 1956-2000. Journal of Natural Resources, 2006, 21(1): 31-44. |
| [63] |
Limjirakan S, Limsakul A. Trends in Thailand pan evaporation from 1970 to 2007. Atmospheric Research, 2012, 108: 122-127. DOI:10.1016/j.atmosres.2012.01.010 |
| [64] |
Li X, Lang Q, Lei K et al. Variation characteristics of pan evaporation and the influencing factors in the Yongding River Basin during 1958-2018. Climatic and Environmental Research, 2021, 26(3): 323-332. [李秀, 郎琪, 雷坤等. 1958—2018年永定河流域蒸发皿蒸发量的变化特征及其影响因子分析. 气候与环境研究, 2021, 26(3): 323-332.] |
| [65] |
Li XH, Gu GH, Yu SL et al. Chang trend of water surface evaporation magnitude in Yunnan Province and its influential factors. Yangtze River, 2020, 51(S2): 63-67. [李学辉, 谷桂华, 余守龙等. 云南省水面蒸发量变化趋势及其影响因素分析. 人民长江, 2020, 51(S2): 63-67.] |
| [66] |
Xie RH, Wang AH, Hua W. Temporal and spatial distribution characteristics and influencing factors of pan evaporation in China from 1961 to 2013. Climatic and Environmental Research, 2020, 25(5): 483-498. [谢睿恒, 王爱慧, 华维. 1961—2013年中国蒸发皿蒸发量时空分布特征及其影响因素. 气候与环境研究, 2020, 25(5): 483-498.] |
| [67] |
Vallet-Coulomb C, Legesse D, Gasse F et al. Lake evaporation estimates in tropical Africa (Lake Ziway, Ethiopia). Journal of Hydrology, 2001, 245(1/2/3/4): 1-18. DOI:10.1016/S0022-1694(01)00341-9 |
| [68] |
Jhajharia D, Shrivastava SK, Sarkar D et al. Temporal characteristics of pan evaporation trends under the humid conditions of northeast India. Agricultural and Forest Meteorology, 2009, 149(5): 763-770. DOI:10.1016/j.agrformet.2008.10.024 |
| [69] |
Oguntunde PG, Abiodun BJ, Olukunle OJ et al. Trends and variability in pan evaporation and other climatic variables at Ibadan, Nigeria, 1973-2008. Meteorological Applications, 2012, 19(4): 464-472. DOI:10.1002/met.281 |
| [70] |
Wang ML, Zhang Y, Lu Y et al. Detection and attribution of reference evapotranspiration change (1951-2020) in the Upper Yangtze River Basin of China. Journal of Water and Climate Change, 2021, 12(6): 2624-2638. DOI:10.2166/wcc.2021.011 |
| [71] |
Xiao K, Griffis TJ, Baker JM et al. Evaporation from a temperate closed-basin lake and its impact on present, past, and future water level. Journal of Hydrology, 2018, 561: 59-75. DOI:10.1016/j.jhydrol.2018.03.059 |
| [72] |
Woolway RI, Kraemer BM, Lenters JD et al. Global lake responses to climate change. Nature Reviews Earth & Environment, 2020, 1(8): 388-403. DOI:10.1038/s43017-020-0067-5 |
| [73] |
Javed A, Cheng VYS, Arhonditsis GB. Detection of spatial and temporal hydro-meteorological trends in Lake Michigan, Lake Huron and Georgian Bay. Aquatic Ecosystem Health & Management, 2019, 22(1): 1-14. DOI:10.1080/14634988.2018.1500850 |
| [74] |
Helfer F, Lemckert C, Zhang H. Impacts of climate change on temperature and evaporation from a large reservoir in Australia. Journal of Hydrology, 2012, 475: 365-378. DOI:10.1016/j.jhydrol.2012.10.008 |
| [75] |
El-Mahdy MES, El-Abd WA, Morsi FI. Forecasting lake evaporation under a changing climate with an integrated artificial neural network model: A case study Lake Nasser, Egypt. Journal of African Earth Sciences, 2021, 179: 104191. DOI:10.1016/j.jafrearsci.2021.104191 |
| [76] |
Lazhu, Yang K, Wang JB et al. Quantifying evaporation and its decadal change for Lake Nam Co, central Tibetan Plateau. Journal of Geophysical Research: Atmospheres, 2016, 121(13): 7578-7591. DOI:10.1002/2015JD024523 |
| [77] |
Xu JQ, Yu SM, Liu JS et al. The implication of heat and water balance changes in a lake basin on the Tibetan Plateau. Hydrological Research Letters, 2009, 3: 1-5. DOI:10.3178/hrl.3.1 |
| [78] |
Du Q, Liu HZ, Liu Y et al. Factors controlling evaporation and the CO2 flux over an open water lake in southwest of China on multiple temporal scales. International Journal of Climatology, 2018, 38(13): 4723-4739. DOI:10.1002/joc.5692 |
 2022, Vol. 34
2022, Vol. 34 

