近年来随着气候变化及人类活动影响加剧，特别是在梯级水库群建设、航道整治、岸线开发等人类活动干扰下，河道在主槽下切的同时，也出现了洪水河槽萎缩、河漫滩减少和洪水位抬升现象^[1-2]，逐渐改变水位流量关系的固有机理，影响泄流能力^[3-4]. 同时下游河道断面水位变化会直接改变水面比降，尤其在大洪水时期，受回水顶托影响，下游水位过高会溯源壅高上游水位，抬高同流量洪水水位，增加洪灾风险^[5-6]. 2020年长江流域发生仅次于1954和1998年的流域性大洪水，长江中游干流洪水位普遍表现出水位高、历时长、超警多、范围广、影响大等特征，汉口以下江段水位超警时间在35 d以上，超警范围及持续时间均超1998年同期水平，其中鄱阳湖汇流顶托严重致使洪水宣泄不畅是长时间维持高洪水位的主要原因之一^[7-8]. 因此准确辨识变化环境下河道水文关系变化，特别是揭示受下游回水或汇流顶托影响的水位变化关联性机制，是开展流域防洪减灾工作的基础.

分析回水或汇流顶托影响需从水位流量关系入手. 河道水位流量关系可分单线型和多线型. 单线型关系多采用实测资料或曼宁、谢才、堰流等公式拟定，适用于不受回水顶托影响河段；对于受回水顶托影响河段，常引入多值型关系，以下游水位作为控制因子，通过多组水位流量关系单线族，间接反映水位流量变化机制^[9-10]. 如Yen和Gonzalez-Castro^[9]基于恒定流公式，提出了河道水力特性图(hydraulic performance graphs，HPG)来定量描述上下游水位和流量的多值关系，在国外得到广泛推广，但建立该特征图需进行不同情景的水面线计算及获取地形、糙率等大量基础资料；孙昭华等^[10]进一步对构建HPG的基础模型进行改建，在仅考虑流量及下游水位条件下实现水位变幅模拟，虽简化了基础资料输入，但改建后的模型精度有待验证，且忽视对回水顶托影响的量化分析. 由于长江中游河段比降总体平缓，沙市至九江段水位易受洞庭湖、鄱阳湖等通江湖泊汇流顶托影响，故通过对下游水位顶托进行量化分析，可进一步准确厘清长江高洪水位的成因机制.

目前学界针对通江湖泊对长江的顶托分析方法多集中在统计指数的定性分析上，如陈栋等^[11]依托水面比降，以顶托消落比表征洞庭湖对长江的顶托作用，认为当长江流量小于6000 m³/s时，湖对江均表现出顶托作用；邴建平等^[12]通过定义顶托强度指数评价了鄱阳湖出流对湖口江段的顶托作用，定性上刻画了江湖水量互补的交换状态；胡振鹏等^[13]进一步依托长江汉口和鄱阳湖星子水文资料，阐明了长江与鄱阳湖的水文关系，但仅侧重揭示长江对鄱阳湖出流顶托作用的临界阈值，未量化评价鄱阳湖对长江中上游水位的顶托影响. 现有众多研究虽可客观揭示通江湖泊对长江的顶托作用，特别是水动力学模型可较精细化模拟河湖水流变化过程，为解析河湖顶托作用提供了强有力工具. 但多数集中在江湖关系分析上，较少从顶托影响的贡献度出发，深入剖析回水或汇流顶托的响应机制，特别是对长江与通江湖泊上下游水力关联性机理的挖掘还不够深入.

三峡水库自2008年正常蓄水运行以来已有10余年，河道水力关系调整引发洪枯水位变化备受关注，特别是鄱阳湖流域2016和2020年发生大洪水，对湖口以上长江中游江段中高洪水位的顶托作用十分明显^[14-15]，其伴随的顶托响应机制研究还不够透彻. 在此背景下，针对上述研究瓶颈及长江中游防洪需要，本文从水文过程仿真及顶托响应评价入手，提出了一种汇流顶托对水位影响的量化分析方法. 同时，立足长江中游汉口河段，尝试从多线型水位流量关系入手，构建考虑汇流顶托影响的水文仿真模型，对汇流顶托响应强度进行量化，绘制响应特性曲线，尝试定量解析鄱阳湖汇流顶托对长江水位变化的影响，以期更好地为长江中下游防洪减灾工作提供技术支撑.

1 研究区及数据

长江中游武汉至湖口江段(武—湖)位于长江中游干流下段，全长约298 km，下游连接中国最大的淡水湖泊——鄱阳湖，其湖区面积约4436 km². 作为长江中下游典型通江湖泊，长江与鄱阳湖间相互顶托造就了复杂的水量交换关系. 当长江水位涨率低于湖区水位涨率时，湖对江的顶托作用明显加强，易使武—湖江段水位抬高，影响泄流能力；当长江水位涨率高于湖区水位涨率时，湖对江的顶托作用减弱，而江对湖的顶托作用则增强，一旦江对湖的顶托过剩，往往发生长江水倒灌鄱阳湖现象^[16-17].

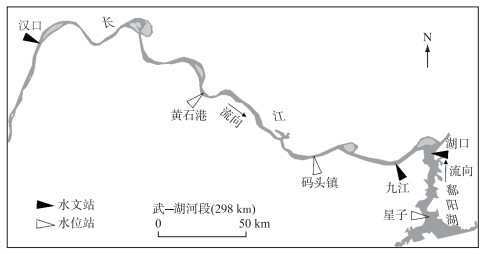
根据长江中游水系及水文(水位)站网分布(图 1)，武—湖江段沿线布设有汉口、九江水文站及黄石港、码头镇等水位站，鄱阳湖出口段还设有湖口水文站和星子水位站. 在经历上游荆江裁弯、航道整治及三峡、葛洲坝等枢纽建设运行后，2008年以来长江中游河段受水利工程影响逐渐进入相对稳定期. 为综合反映21世纪以来，特别是三峡水库正常蓄水运行后鄱阳湖汇流对武—湖江段水位的顶托影响，拟结合河段水文资料的实际情况，确定武—湖江段为主要研究区，并选取汉口站作为长江中游干流控制站，星子站作为鄱阳湖区水位代表站，以各站2008—2020年逐日水文资料开展分析研究. 各站水文资料均摘自已经出版的水文年鉴或整编资料^[18]，能够满足本研究精度要求.

2 量化分析方法

汇流顶托量化分析方法包括水文过程仿真模型和响应评价指数两部分. 结合长江中游河道水力特征，研究以明渠恒定渐变流假设为前提，基于水力学及河流动力学原理，推导并构建考虑汇流顶托的水文过程仿真模型. 在此基础上进一步定义响应评价特征指数及影响贡献率，量化评价水位变化的影响.

2.1 水文过程仿真模型

对于明显受回水或汇流顶托影响的河段，国内外规范中均推荐如下模型关系式^[19-20]：

$ \frac{Q_{\mathrm{n}}}{Q_{\text {ref }}}=c\left[\frac{\Delta Z_{\mathrm{n}}}{\Delta Z_{\mathrm{ref}}}\right]^d $

(1)

式中，Q_n、Q_ref分别为特定水位下待求流量和某一参考基准流量；ΔZ_n、ΔZ_ref为与Q_n、Q_ref相应的落差，由上下游同时刻水位得到；c、d为模型参数.

考虑到式(1)需参考基准流量以及各种辅助曲线计算，计算繁琐，且在不规则河道上难以通过流量推算水位. 针对这一缺点，文献[10]对式(1)进行改进，主要结合长江中游河道具体特性，引入明渠恒定渐变流方程，以水面比降代替能坡，再耦合河宽和水深的非线性关系，对式(1)进行简化，最终推导得到关系式(2). 具体推导过程可参考文献[10]，本次不赘述.

$ \frac{Q_{\mathrm{n}}}{Q_{\text {ref }}}=\frac{C A \sqrt{h}}{C_{\text {ref }} A_{\text {ref }} \sqrt{h_{\text {ref }}}} \sqrt{\frac{\partial Z / \partial x}{(\partial Z / \partial x)_{\text {ref }}}} \approx \sqrt{\frac{Z_{\mathrm{u}}-Z_{\mathrm{d}}}{\left(Z_{\mathrm{u}}-Z_{\mathrm{d}}\right)_{\text {ref }}}} $

(2)

式中，C为谢才系数，C=h^1/6/n，n为糙率，h为断面平均水深；A为过流断面面积；h_ref为参考断面平均水深；Z_u为上游断面水位，Z_d为下游断面水位.

式(2)是假设河段水流为明渠恒定渐变流基础上得到的. 由于长江中游河段洲滩密布，河道深泓起伏，计算河段过程并不完全满足该假设条件，从而影响模拟精度.

针对以武—湖河段为代表的河道特征，本次拟对式(2)进行改建. 考虑到河段长度越短，河道水流特征越贴近明渠恒定渐变流. 基于此条件，将总长为l的计算河段，共划分i段，每段水流条件满足式(2)关系，则有：

$ \frac{Q_{\mathrm{n}}}{Q_{\text {ref }}}=\sum\limits_{k=1}^i \sqrt{\frac{Z_{\mathrm{u}}(k)-Z_{\mathrm{d}}(k)}{\left[Z_{\mathrm{u}}(k)-Z_{\mathrm{d}}(k)\right]_{\mathrm{ref}}}} / i $

(3)

式中，k=1, 2, 3…i, i为总分段数.

河道内存在平均情况下的近似“正常流”状态，该状态下[Z_u(k)-Z_d(k)]_ref为定值，可由单值型水位流量关系式推求^[19]，即：

$ Q_{\text {ref }}=a\left(Z_{\mathrm{u}}-Z_0\right)^b \; {\rm{或}}\;Z_{\mathrm{u}}=\left(Q_{\text {ref }} / a\right)^{1 / b}+Z_0 $

(4)

式中，Z₀为特定断面参数；a、b为特定参数.

将式(4)代入式(3)，在平均情况下每段内的[Z_u(k)-Z_d(k)]_ref为定值，用符号A表示. 同时对右式进行近似处理，则可将式(4)转化为：

$ \frac{Q}{a\left(Z_{\mathrm{u}}-Z_0\right)^b}=\frac{\sum\limits_{k=1}^i \sqrt{Z_{\mathrm{u}}(k)-Z_{\mathrm{d}}(k)}}{\sqrt{A} i} \approx c\left(Z_{\mathrm{u}}-Z_{\mathrm{d}}\right)^\beta $

(5)

式中，c和β为待定参数.

令a×c为α，将式(5)进一步变换得到：

$ Q=\alpha\left(Z_{\mathrm{u}}-Z_{\mathrm{d}}\right)^\beta\left(Z_{\mathrm{u}}-Z_0\right)^b $

(6)

式中，Q为河段上断面流量；Z_u为河段上断面水位，Z_d为河段下断面水位或河湖连通的湖口或湖区水位，表征回水或汇流顶托控制因子；Z₀、α、β和b均为模型待定参数，其中Z₀是反映上游断面特征的特定参数.

式(6)为最终改建推导得到的考虑下游回水或汇流顶托的水文仿真模型，可视为经验计算式，仅需水位作为输入即可推求流量，结构简单，计算方便. 由于是基于明渠恒定渐变流方程为前提进行推导，模型α、β和b系数总体上反映了河段地形、糙率等特性，隐含一定物理基础，此外Z₀可直观视为流量为0时的断面平均水位，反映断面附近河床高程. 本文统一将式(6)记为HMCJ模型(hydrological model considering converge-jacking).

要准确构建HMCJ模型，则可凭借河段长系列进口流量及上下游水位资料，即可共同率定得到Z₀、α、β和b 4个待定参数. 在模型参数确定基础上，利用式(6)可由河段上下游同期水位直接推求相应河段进口流量. 同时，在进口流量及下游水位确定情况下，亦可通过试算法，反推上游进口断面水位，从而实现考虑下游汇流影响的水位过程模拟.

2.2 响应评价指数及贡献率 2.2.1 流量响应指数

对于受顶托影响河段，根据HMCJ模型，其水位流量关系可记为Z_u=f(Q, Z_d). 显然当Z_d为常数时，Z_u变化仅与流量Q有关，相应水位流量关系即为稳定的单值型关系. 在此条件下，假设Z_d不变，可定义流量响应指数J_q为：

$ J_{\mathrm{q}}=\frac{\Delta_{\mathrm{qu}}}{\Delta_{\mathrm{q}}}=\frac{f\left(Q+\Delta_{\mathrm{q}}, Z_{\mathrm{d}}\right)-f\left(Q, Z_{\mathrm{d}}\right)}{\Delta_{\mathrm{q}}}, \Delta_{\mathrm{q}} \geqslant 0 $

(7)

式中，Δ_q表示流量变化值；Δ_qu表示在下游水位一定时，流量变化引起的上游水位变化，即流量变化影响. J_q为流量响应指数，无量纲数，大于0. J_q值越大，表明水位对流量变化的响应越敏感.

2.2.2 顶托响应指数

若在流量不变条件下，因下游水位变化引起上游水位的变化，可认为是下游回水或汇流顶托带来的响应. 引起的水位变幅越大，顶托响应强度就越强，则可定义顶托响应指数J_z，以量化表征顶托强度的变化特征：

$ J_{\mathrm{z}}=\frac{\Delta_{\mathrm{zu}}}{\Delta_{\mathrm{d}}}=\frac{f\left(Q, Z_{\mathrm{d}}+\Delta_{\mathrm{d}}\right)-f\left(Q, Z_{\mathrm{d}}\right)}{\Delta_{\mathrm{d}}}, \Delta_{\mathrm{d}} \geqslant 0 $

(8)

式中，Δ_d表示下游水位变化值；Δ_zu表示流量一定时，下游水位变化引起的上游水位变化，即回水或汇流顶托影响. J_z为顶托响应指数，无量纲数，大于0. J_z值越大，表明下游回水或汇流顶托响应越敏感.

2.2.3 综合影响贡献率

上文提出的水文仿真模型仅考虑进口流量及下游回水或汇流顶托影响，忽略了其他影响因子，如区间入汇、沿江排涝、模型误差等，故其模拟水位与实际水位存在偏差. 假设模型精度足够高，则模型误差将足够小，其模拟水位与实际水位偏差记为Δ_s，可近似表征其他因素干扰影响，可由下式计算：

$ \Delta_{\mathrm{s}}=Z_{\mathrm{u}}-Z_{\mathrm{us}}=Z_{\mathrm{u}}-f\left(Q, Z_{\mathrm{d}}\right) $

(9)

式中，Z_us为HMCJ模型模拟值. 则可定义综合影响贡献率：

$ \left\{ {\begin{array}{*{20}{l}} {{\rho _{\rm{q}}} = \frac{{{\Delta _{{\rm{qu}}}}}}{\Delta } = \frac{{{\Delta _{{\rm{qu}}}}}}{{\left| {{\Delta _{{\rm{zu}}}}} \right| + \left| {{\Delta _{{\rm{qu}}}}} \right| + \left| {{\Delta _{\rm{s}}}} \right|}} \times 100\% }\\ {{\rho _{\rm{z}}} = \frac{{{\Delta _{{\rm{zu}}}}}}{\Delta } = \frac{{{\Delta _{{\rm{zu}}}}}}{{\left| {{\Delta _{{\rm{zu}}}}} \right| + \left| {{\Delta _{{\rm{qu}}}}} \right| + \left| {{\Delta _{\rm{s}}}} \right|}} \times 100\% }\\ {{\rho _{\rm{s}}} = \frac{{{\Delta _{\rm{s}}}}}{\Delta } = \frac{{{\Delta _{\rm{s}}}}}{{\left| {{\Delta _{{\rm{zu}}}}} \right| + \left| {{\Delta _{{\rm{qu}}}}} \right| + \left| {{\Delta _{\rm{s}}}} \right|}} \times 100\% } \end{array}} \right. $

(10)

式中，ρ_q为流量影响贡献率；ρ_z为顶托影响贡献率；ρ_s为其他影响贡献率；Δ表示综合影响值.

一般要推求某时刻水位的综合影响贡献率，首先需确定比较基准，再推求相对于基准的各影响因子变化带来的水位响应值，从而可运用式(10)推求各因子的影响贡献率.

3 实例应用分析 3.1 汉口水文过程仿真模拟

为尽量突出鄱阳湖顶托对长江武汉江段水位变化的影响，经综合比选分析，选取星子水位表征鄱阳湖来水入汇的顶托控制因子. 针对汉口站同期实测流量，在日时间尺度上构建HMCJ模型. 模型以汉口流量为目标输出，以汉口、星子水位为模型输入，设定2008—2017年为率定期，2018—2020年为检验期，采用SCE-UA算法自动优选模型参数. SCE-UA算法综合了确定性搜索、随机搜索和生物竞争进化等方法的优点，是一种全局优化算法^[21]. 模型参数优选的目标函数f是径流总量相对误差RE(relative error)的绝对值与确定性系数DC(deterministic coefficient)之差最小^[22-23]，计算式如下：

$ \min f=|R E|-D C $

(11)

其中：

$ DC = 1 - \frac{{\sum\limits_{i = 1}^n {{{\left( {{Q_{{\rm{s}}i}} - {Q_{{\rm{o}}i}}} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left( {{Q_{{\rm{o}}i}} - {{\bar Q}_{\rm{o}}}} \right)}^2}} }}, \;\;RE = \frac{{\sum\limits_{i = 1}^n {{Q_{{\rm{s}}i}}} }}{{\sum\limits_{i = 1}^n {{Q_{\rm{o}}}} }} - 1 $

(12)

或：

$ DC = 1 - \frac{{\sum\limits_{i = 1}^n {{{\left( {{Z_{{\rm{s}}i}} - {Z_{{\rm{o}}i}}} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left( {{Z_{{\rm{o}}i}} - {{\bar Z}_{\rm{o}}}} \right)}^2}} }}, \;\;RE = \frac{{{{\bar Z}_{\rm{s}}}}}{{{{\bar Z}_{\rm{o}}}}} - 1 $

(13)

式中，Q_oi、Q_si或Z_oi、Z_si分别表示第i时段流量或水位观测值与模型模拟值；Q_o为n时间段内流量观测值的平均值；Z_s、Z_o分别表示n时间段内水位观测值与模型模拟值的平均值；n为日段数.

HMCJ模型参数优化结果及精度指标如表 1所示，其中DC₁、DC₂分别表示率定期、检验期的确定性系数，RE₁、RE₂分别表示模型率定期、检验期的径流总量或平均水位相对误差. 由表 1可知，无论检验期还是率定期，确定性系数DC均达到0.98，|RE|控制在3%之内，说明模型模拟精度较高.

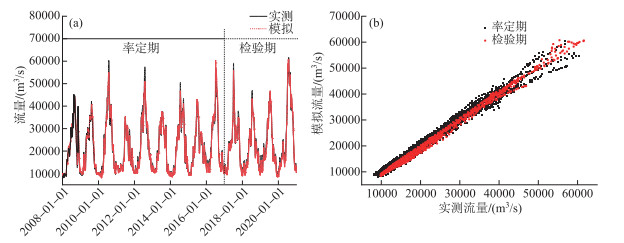
图 2给出汉口站2008—2020年逐日流量模拟过程. 由该图可知，模型模拟日径流过程与实测过程具有很好的一致性，模型在枯水年、丰水年都能够较好地再现日径流变化过程，模拟效果良好.

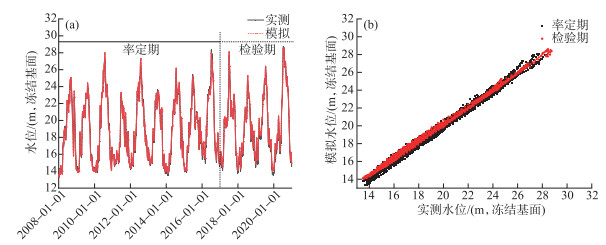
在模型参数确定基础上，以汉口站流量及下游星子水位作为模型输入，通过逐时段试算反推汉口水位，模拟计算结果见图 3，相应的精度指标如表 1所示. 从水位精度评价指标及过程看，检验期确定性系数DC达到0.99，|RE|控制在1%之内，高洪水位模拟值与实测更加贴近，说明模型对水位的模拟精度更高.

3.2 水位变化的关联性响应

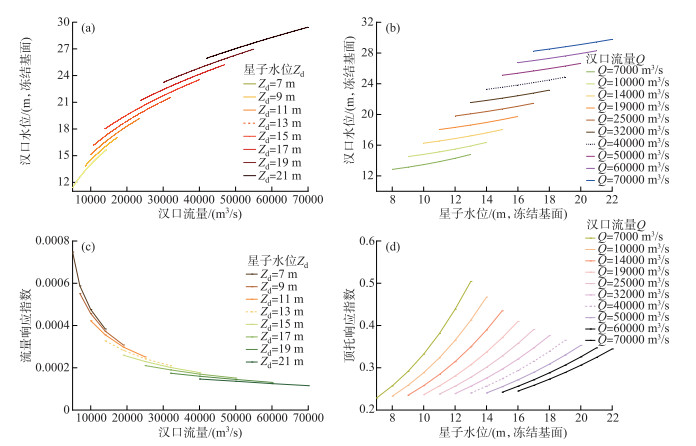
根据已构建的水文仿真模型，分别以星子水位(Z_d)或汉口流量(Q)作为控制因子，模拟不同流量或水位级下的汉口水位(Z_u)变化，并绘制等值线图，得到仅考虑鄱阳湖顶托的汉口多值型水位流量关系响应特征曲线(图 4)，其中星子水位代表鄱阳湖区水位变化.

如图 4所示，在鄱阳湖星子水位一定情况下，汉口水位流量呈单值线型的正相关关系，总体表现出水位随流量的增大而增大；而流量响应指数J_q变幅在0.0001~0.0008之间，随流量的增加而减少. 如以Z_d=13 m线为例，流量由14000 m³/s增加至32000 m³/s时，J_q则由0.00033降低至0.00021，表现出负相关关系. 若在此基础上Z_d值抬高至17 m，溯源壅高带来的汇流顶托强度增强，从而会相对削落流量对水位变化的敏感性，故J_q由0.00021降低至0.00019. 同理，在河道流量相同条件下，汉口水位与鄱阳湖星子水位亦呈单调正比关系，即星子水位越高，汇流顶托强度亦越大，从而壅高上游水位，使得顶托响应指数J_z亦相应增加，整体变幅在0.25~0.55之间. 以Q=40000 m³/s线为例，当Z_d由14 m增加至19 m时，J_z则由0.24增加至0.36. 若在此基础上流量增加至60000 m³/s，流量影响增强将相对削落汇流顶托影响，故J_z由0.36降低至0.31，顶托强度有所降低.

显然，通过图 4所示的考虑鄱阳湖顶托的汉口水位流量关系及其响应特征曲线，能够直观呈现鄱阳湖与长江汉口水位变化的关联性机制，并量化揭示鄱阳湖汇流顶托对长江水位的影响.

3.3 典型年汇流顶托影响分析

受江湖关系影响，鄱阳湖汇流长期对湖口以上江段有一定的顶托作用，特别是当遭遇长江中游洪水后，鄱阳湖汇流顶托影响将更加明显，如2016、2020年汛期长江流域均发生流域性大洪水，恰逢鄱阳湖与长江洪水发生遭遇，导致其汇流顶托是湖口以上江段长时间维持高洪水位的主因之一^[14-15]. 因此，本次以2016、2020年洪水为典型，运用已构建的水文仿真模型及影响贡献率计算式，尝试开展鄱阳湖汇流顶托影响定量分析.

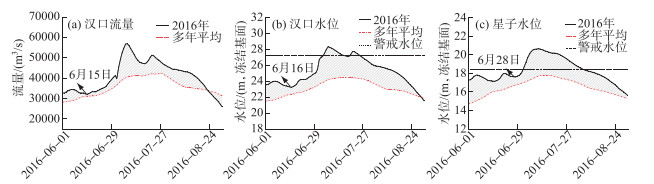
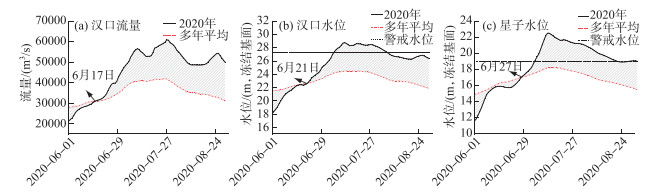
分析前首先确定比较基准. 本文认为年均条件下的河段水位流量关系近似达到平衡，以此作为基准可反映河段水流条件的日常态势. 图 5和图 6分别给出汉口、星子站2016年和2020年6—8月期间水位、流量变化过程及其年均过程(2008—2020年). 由图可知，以汉口为代表的长江水位自6月中上旬快速起涨以来，整个7月长时间维持超警水位，较年均水位涨幅在0~4.30 m之间，其中2020年水位直至8月中旬才降至警戒水位以下；与此同时，长江下游遭遇鄱阳湖大洪水，星子水位在6月下旬至8月下旬期间均超年均水位，涨幅在0~4.33 m之间，从而对长江中上游水位产生明显顶托效应. 经典型年洪水过程综合比较判断，统一选取6月28日—8月18日作为本次实例分析时段，且该段时期内鄱阳湖湖口发生倒灌天数不超过5 d，说明该时段内绝大部分时间以湖对江的顶托作用为主，且作用强烈，分析结果具有一定的参考价值.

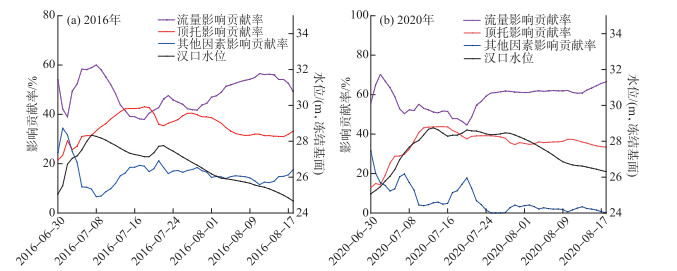
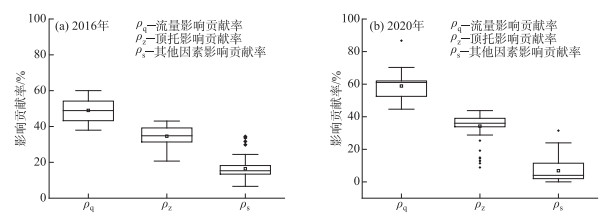
其次运用已构建的水文仿真模型及影响贡献率计算式，逐时段计算各因子影响贡献率. 图 7和图 8分别给出了2016和2020年洪水分析时段内鄱阳湖顶托影响贡献率变化曲线及其箱形图，表 2给出了汉口江段特征水文条件下鄱阳湖顶托影响定量评估结果.

6月28日—8月18日洪水期间，2016年鄱阳湖汇流顶托对汉口水位变化影响的平均贡献率为34.5%，长江来水影响平均贡献率为48.8%，其他因素平均贡献率为16.7%. 当汉口达最大日均流量时，水位变化主要受长江来水及鄱阳湖汇流顶托影响，贡献率分别为60.0%和33.4%；当汉口现最高日均水位时，水位变化还受区间汇流、沿江排涝等其他因素影响，其中鄱阳湖汇流顶托贡献率为31.4%，长江来水贡献率为58.9%，其他因素贡献率为9.7%. 2020年鄱阳湖汇流顶托影响与2016年基本相当，但长江来水平均影响贡献率有所增加，为58.1%，其他因素平均贡献率则有所降低，为5.8%. 当汉口现最高日均水位时，水位变化主要受长江来水及鄱阳湖汇流顶托影响，贡献率分别为51.1%和43.7%，其他因素贡献率仅为5.2%(表 2).

值得注意的是，当鄱阳湖来水较小、武—湖区间来水较大时，鄱阳湖顶托影响将不及区间汇流或沿江排涝影响. 如2016年6月28日—7月3日期间武—湖区间洪水量较大，举水流域的柳自港站7月1日19:00出现洪峰5500 m³/s，巴水流域马家潭站7月2日1:00出现最大洪峰7460 m³/s，使得该时期内区间汇流等其他因素影响贡献率最高可达34.4%，大于相应鄱阳湖顶托影响(23.4%).

综上分析，在2016和2020年洪水条件下，汉口江段长历时高洪水位形成的主要因素是长江来水量大及鄱阳湖汇流顶托，二者合力贡献可达83.3%以上，其中鄱阳湖汇流顶托贡献在35%左右；其余因素(如武—湖区间洪水、沿江排涝等)亦助推高洪水位形成，其中对2016年洪水平均贡献率可达16.7%，部分时段贡献可达34.4%.

4 结论

为量化评估鄱阳湖汇流顶托对长江水位变化的响应机制，本文尝试从多线型水位流量关系入手，改进提出了一种考虑汇流顶托的水文仿真模型，并定义了顶托响应指数及影响贡献率，提出了汇流顶托量化分析方法，开展了鄱阳湖汇流顶托对长江汉口江段水位变化的量化分析. 主要结论包括：

1) 针对长江中游河段水力特性，改进并提出了一种考虑下游顶托影响的水文仿真模型，并应用于汉口江段水文过程模拟. 结果表明，该模型结构简单，计算方便，通过SCE-UA算法自动优选参数后，确定性系数可达0.98以上，总量相对误差在±3%以内，模型模拟精度较高，能够较好的再现目标河段水位、流量变化过程.

2) 定义了流量响应指数及顶托响应指数，提出了综合影响贡献率计算式；根据已构建的汉口水文仿真模型，分别以星子水位或汉口流量作为控制因子，研制了汉口多值型水位流量关系及其响应特征曲线，进一步揭示了鄱阳湖与长江汉口江段水位变化的关联性机制.

3) 以2016和2020年洪水过程为例，尝试定量解析鄱阳湖汇流顶托对长江汉口水位的影响贡献. 经分析，汉口江段长历时高洪水位形成的主要因素是长江来水量大及鄱阳湖汇流顶托导致，二者合力贡献可达83.3%以上；其余因素(如区间洪水、沿江排涝等)亦助推高洪水位形成，部分时段贡献可达34.4%.

基于本文提出的汇流顶托量化分析方法，可定量评估因回水或汇流顶托引起的水位变化，对于解析河段高洪水位成因机制提供了有效的技术支撑. 但研究提出的水文仿真模型是以恒定渐变流假设为前提的，忽略了区间入汇项，一定程度上影响模型精度. 今后有必要引入区间汇流，以进一步提高模型普适性及模拟精度.