(2: 河南工程学院计算机学院,郑州 451191)
(3: 中国科学院大学中丹学院,北京 100049)
(4: 重庆三峡学院环境与化学工程学院,万州 404000)
(2: College of Computer, Henan University of Engineering, Zhengzhou 451191, P.R.China)
(3: Sino-Danish College, University of Chinese Academy of Sciences, Beijing 100049, P.R.China)
(4: College of Environmental and Chemical Engineering, Chongqing Three Gorges University, Wanzhou 404000, P.R.China)
植物根系的演变是植物从水生环境迁移到陆生环境的基础,并最终导致叶片合成糖类和根系供应资源(主要是水分和营养)之间功能上的分割[1]. 作为植物三大营养器官之一,根系在生物圈物质循环、能量流动和信息传递中都起到关键性作用[2-3]. 根系的作用已日益引发关注,被称作“被隐藏的一半”[1, 4]. 根系构型在植物资源利用中起重要作用[5]. 植物根系构型是指根系在其生长环境中的形状和分布,包括同一根系的各种根在介质中沿根轴的二维平面分布(平面几何构型)和不同类型的根系在介质中的三维空间分布(立体几何构型)[6-7],这2种构型都可以通过根系拓扑指数表现出来[8]. 当前对植物根系构型研究方法可分为两大类:第一类方法是通过扫描或微根管法(Minirhizotron)获取植物真实根系构型后再通过软件(WinRhizo、SimRoot等)分析根系形态和拓扑指标. 该方法获取的数据较为真实,可获得根系连续生长数据,且通过对根系二维构型建模可以反映根系三维立体几何构型[9]. 第二类方法是先通过构建植物形态和结构的模型对植物的形态结构进行量化研究,总结出植物生长的规律,根据植物生长情况对植物根系构型模型进行修正的基础后,再用适当的方式对植物的形态结构进行量化表达,这种方法可以简化根系模型,减少计算量,以通过计算机模拟重现植物根系发育过程的L系统为代表,可以较好模拟植物生长状况[10-12].
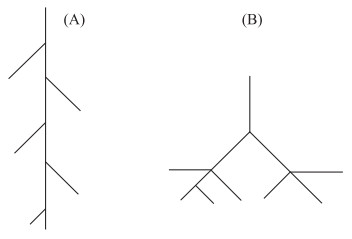
第一类方法针对根系的二维平面几何构型已有较多的研究,Fitter等提出了两种典型的植物根系二维几何构型:鱼骨状构型(herringbone branching)(图 1A)和叉状分支构型(dichotomous branching)(图 1B)[13]. 通过对植物根系进行高精度扫描得到根系图像,之后通过根系测量分析软件对图像进行处理,利用统计学方法分析得出根系二维构型数据:所有外部连接总和μ和植物整条根系中最大的从基部到外部连接的外部连接的个数a(根系最大路径长度),以此计算根系拓扑指数TI、qa和qb. 对于鱼骨状构型,其拓扑指数TI接近1,qa和qb接近1,而叉状分支构型拓扑指数TI接近0.5,qa和qb接近0[13-14]. 植物根系构型理论认为具有鱼骨状构型的根系(图 1A)的植物适应于低营养生境,原因在于这种根系构型有较多和较长的连接,根系分级低,可以吸收土壤深层的营养和水分,根系在争夺空间和资源上由于较低的根系间竞争而更有效率;但是这种构型的根系传输效率较低,构建需要的代价较高[15]. 叉状分支构型根系(图 1B)连接较短,与鱼骨状构型相比容易构建和维持,但由于根系间存在对营养和水分的竞争导致根系传递效率不高,这种构型的根系一般出现在营养和水分较为丰富的生境[14, 16]. 挖掘的方法获取植物根系工作量大,对于森林中乔木根系只能通过局部挖掘来反映根系情况,无法获取全部根系. 通过植物根系二维构型来构建根系三维构型不可避免地会导致根系部分信息缺失[17]. 此外这种根系模型也较难适用于已经完成生长的根系[18]. 目前植物根系的研究方法中常用的微根管法能够非接触地获取根系结构信息[19],针对小麦和大豆作物已经进行了大量研究. 然而微根管法只适用于陆生植物,水生植物根系埋藏于饱含水分的底质中,较难通过微根管法实时传输数据研究. 因此之前对于水生植物根系研究更多地聚焦于根系形态特征和功能性状,对根系结构关注相对较少,更缺乏根系动态生长模型的报道.
|
图 1 植物根系结构鱼骨状构型(A)和叉状分支构型(B)示意图 Fig.1 Sketches of plant root structure of the herringbone branching (A) and dichotomous branching (B) |
第二类方法以通过计算机模拟重现植物根系发育过程的L系统为代表,可以较好模拟植物生长状况. L系统由Aristid Lindenmayer于1968年提出并以他的名字首字母命名[20],之后被Prusinkiewicz等发展用于植物和植物器官的生长模拟,其主要思想和方法集中体现于《植物的算法美》(The Algorithmic Beauty of Plants)一书中[21]. 这一类方法应用在陆生植物根系构型的模拟建立在植物结构具有对称性(symmetry)和自相似性(self-similarity)两大前提条件上,也就是植物组织结构的几何形状在局部和整体上具有相似性[22],应该说从这两个假设出发建立的根系构型模型能较好地符合实际情况,在植物叶镶嵌、茎分枝和花序的模拟结果较好. 通过植物局部根系模拟整体根系特征,动态地对水稻等植物根系在多种营养条件下的三维空间模型构建,可以较好地表征根系拓扑结构[12]. 然而目前有研究发现水生植物凤眼莲(Eichhornia crassipes)的根系能较好地满足对称性假设,却并不满足自相似性假设[23]. 凤眼莲单独一条二级根系所有连接的外部连接总和μ和植物整条根系中最大的从基部到外部连接的外部连接的个数a(根系最大路径长度)相等,即μ=a时,TI=lg a/lg μ=1,qa=qb=1表现为典型的鱼骨状构型[24]. 而凤眼莲局部根系与整体根系在结构上并不一致,其整体根系又由多条鱼骨状构型根系构成一种特殊的叉状分支构型,称作“辐射状聚合构型”[23, 25]. 在另一种水生植物大薸(Pistia stratiotes)中也发现类似的情况. 因此在水生植物中采用L系统建立根系模型,需要考虑根系特殊性,根据情况探讨自相似性在水生植物中的适用性.
本研究拟通过对水生植物根系真实生长指标进行测定,建立根系伸长规则和分支规则,引入根系与根系间角度,通过L系统建立水生植物根系动态生长模型. 之后利用2种分别代表漂浮和沉水植物的凤眼莲和穗状狐尾藻(Myriophyllum spicatum)建立相应的根系动态生长模型,模拟水生植物从幼苗发展为成熟个体,从简单根系发展成复杂根系的生长过程. 本研究将从根系构型这一角度阐述水生植物对水生生境的适应性,也可为水生植物保护、管理和生态修复提供科学依据.
1 材料和方法 1.1 实验材料外来入侵漂浮植物凤眼莲又名水葫芦、凤眼蓝,原产于南美洲亚马逊河流域[26]. 凤眼莲原作为观赏植物引入中国,逸生后在长江流域和南方河流、湖泊等生境水面形成连绵成片的漂浮植毡层,遮蔽阳光,阻隔水体和大气交换,引起沉水植物、鱼类和软体动物等生物死亡,已列入IUCN《100种世界最严重外来入侵物种名录》和第一批《中国外来入侵物种名单(2003)》[27-32]. 目前已经建立了一些凤眼莲模型,如Lorber等的生长和繁殖模型[33]、Gamage等的种群生长模型[34]、Yang等的机载高光谱图像识别模型[35]、Wilson等和Buller等的自然资源评估模型[36-37]、Eid等的根茎叶生长和相互关系模型[30]和Huang等的根系拓扑结构模型[23]. 然而这些模型更多地建立在凤眼莲个体结构和种群增长的模拟,尚无其根系动态生长模型. 凤眼莲的根系非常复杂,重叠很多,常规扫描分析方法无法得到其完整根系. 本研究拟通过剪切其单独根系分别扫描,再组合成根系构型的方法来研究其真实的整体根系结构,建立其根系动态生长模型.
沉水植物穗状狐尾藻,又名穗花狐尾藻、聚藻,在我国南北各地均有分布,生于池塘或河川中,为世界广布种[38-40]. 穗状狐尾藻的根系为典型的叉状分支构型[41]. 由于大多数水生植物根系都是叉状分支构型[41-42],选择这种植物根系进行生长模拟构建具有代表性.
凤眼莲和穗状狐尾藻的培养工作分别在武汉大学梁子湖湖泊生态系统国家野外科学观测研究站(简称“梁子湖站”)和中国科学院太湖湖泊生态系统研究站(简称“太湖站”)完成. 为尽可能模拟这两种植物的自然生长过程,本研究使用了半开放的方法. 凤眼莲培养于梁子湖中由围网围起来的围隔中,水深约2 m, 围隔中的水体与梁子湖湖水相通. 穗状狐尾藻培养于太湖站一个水深约1.5 m的池塘中,池塘通过涵洞与太湖相连. 在研究开始和结束时分别采集这2种植物各30株初始根系和成熟根系进行扫描.
1.2 根系扫描方法凤眼莲为漂浮植物,根系并不与底质接触,可以直接取样. 对于穗状狐尾藻根系,挖掘时从表层土壤开挖,逐步往下延伸,根系附近泥土沿着根系方向去除,一块一块洗掉附着泥土,尽量保持根系形状以免影响根系性状. 获取根系后将植物根茎连接处剪断后,根系用镊子放置在扫描仪上透明水槽(长240 mm, 宽160 mm, 高15 mm)中,加自来水至水槽容积的2/3左右. 用镊子展开根系,使根系处于分散无重叠状态. 一般一次只扫描一条根系;若根系较小,则一次可扫描多条根系. 根系图像使用爱普生12000XL扫描仪(Seiko Epson Corp., Suwa, Nagano, Japan)扫描获取. 根据Bouma等的推荐[43],图像分辨率设置为600 dpi,扫描完成后保存1 ∶1无压缩8 bit高分辨率tiff格式图像. 此扫描仪配备有两种光源:白色LED光源和红外IR光源. 为使根系与背景对照明显,对于接近透明的凤眼莲根系预先使用0.2 mmol/L(0.075 mg/mL)甲烯蓝溶液染色30 s后再使用白色LED光源扫描,背景选用扫描仪内侧配套的白色背景板. 对于浅色的穗状狐尾藻根系使用红外光源,背景为扫描仪内侧配套的无色玻璃. 扫描完成后取出根系,倒出水槽中剩余水分,用自来水冲洗清洁水槽内附着的残留根系后,再用同样的方式扫描下一条根系. 本研究使用WinRHIZO根系测量分析软件(Regent Instruments Inc., Québec City, Canada)对扫描仪扫描后根系图像进行处理,此软件利用统计学方法分析根系图像信息,得出根系形态和结构数据.
1.3 基于L系统的根系动态生长模型构建方法L系统的核心概念主要由公理和迭代置换规则组成. L系统以字符为核心,L系统内部一般用一个字符串表示系统的状态,称为L字符串. 公理表示系统所处的原始状态,即初始L字符串. 可以采用不同的字符对应系统不同的状态. 迭代置换规则又称为产生式p(production),即是L字符串中字符的迭代置换规则,它表示在每个演化周期,系统状态的变化规则. L系统即是基于产生式p,对简单的初始目标部分或全部不断的进行迭代置换从而表达复杂对象的一种方法. 在每个演化周期,L系统应用产生式对系统状态(L字符串)进行修改,形成新的系统状态. 因此L系统的最终结果是一个由具有特殊意义字符组成的字符串. 通过给L系统中每一个字符赋予一个特定的图形含义或者方向说明,从而实现L系统的图形可视化. 考虑仅有两个字母a和b构成的系统ab,假定产生式p为a→ab和b→a,即a被ab置换,b被a置换. 根据规则ab第1次被置换为aba,第2次被置换为abaab,第3次被置换为abaababa,第4次被置换为abaababaabaab,第5次被置换为abaababaabaababaababa……由于植物根系的生长可以看做是一个连续和重复的过程,因此通过L系统可以较好地模拟植物根系的动态生长过程. 计算中全部程序均在Matlab 2021a (MathWorks, Inc., Natick, Massachusetts, USA)中完成编译,所有程序编写均由作者完成.
基于L系统的根系动态生长模型主要包含根系伸长规则和根系分支规则.
根系伸长时具有以下规则:
规则1:当某根系根龄小于等于该根系根寿命(rl(t))时,该根系会一直伸长. 根系长度通过公式(1)计算:
| l(t)=lmax(1−e−rlmaxt) | (1) |
式中,lmax表示该根系最大长度,r表示该根系初始伸长速度,t为该根系根龄;l(t)表示该根系在t时间的长度.
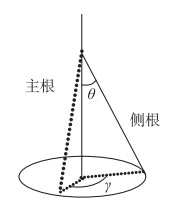
规则2:根系会朝着一定的方向伸长. 初始根系生长方向(R)由主根与侧根(lateral root)的夹角θ和径向角γ确定. 其中夹角θ是从具有用户定义的均值和标准差的正态分布中随机取值;径向角γ表示侧根围绕主根旋转的角度,从0到2π的均匀分布中随机取值(图 2). 在根系生长过程中,为使得生成的根系更加具有随机性,对初始根系生长方向增加随机角度变化. 即长度为Δl的根段生长时,设置根段生长尺度dx(dx < Δl),随后根依据增加随机角度变化的生长方向增长dx长度,直到完成Δl长度生长为止.
|
图 2 根系生长方向 Fig.2 Root growth direction |
根伸长规则通过公式(2)描述:
| GΔt(l,t)−>{RFΔlG(l+Δl,t+Δt)l+Δl<lmaxG(lmax,t+Δt) otherwise | (2) |
式中,符号G代表根生长规则,表示根在当前长度为l,当前时刻为t的条件下,经过生长间隔Δt后的生长变化. 参数l表示通过公式(1)计算的t时间的根长;Δt为根系的生长时间间隔,本研究中设为1天;Δl为经过Δt时间的根长增量;R表示根系生长方向;符号FΔl表示长度为Δl的根段. 通过公式(2)的重复迭代能够完成根系朝着方向R长度为Δl生长.
根系分支时具有以下规则:
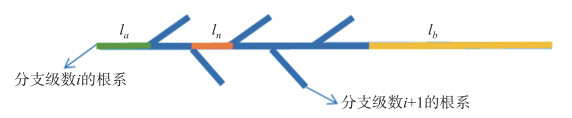
规则3:分支级数为i的根系能够产生分支级数为i+1的侧根,即为根系分支自相似结构. 根系一般分为三块区域:顶端不分支区域(la)、末端不分支区域(lb)和分支区域(ln*N)(图 3). ln为分支级数为i的根系分支间距,N表示分支级数为i的根系最大分支数目.
|
图 3 根系分支自相似结构 Fig.3 Self-similarity structure of root branch |
规则4:当根系长度大于一定阈值,即顶端不分支区域和末端不分支区域长度之和时,会产生分支. 根系产生第j个分支时的根长可以通过公式(3)计算:
| lj=la+lb+(j−1)ln | (3) |
结合公式(1)可以计算出根系产生第j个分支时的延迟时间dj为:
| dj=−lmaxrlg(lmax−ljlmax) | (4) |
根系分支规则通过公式(5)和(6)描述:
| B(j)−>{D(0,dj)j⩽ | (5) |
式中,B表示根分支产生的规则,参数j表示产生的分支为第j个. B(j)代表了第j个分支的产生规则,D表示延迟规则,d是第j个分支的延迟时间,可以通过公式(4)计算. D(0, dj)表示第j个分支经过延时时间dj后,该分支会产生:
| D^{\Delta t}\left(t, t_{\mathrm{end}}\right)-> \begin{cases}B(j+1) G\left(t+\Delta t-t_{\mathrm{end}}, l\left(t+\Delta t-t_{\mathrm{end}}\right)\right) B(1) & t+\Delta t \geqslant t_{\mathrm{end}} \\ D\left(t+\Delta t, t_{\mathrm{end}}\right) & t+\Delta t<t_{\mathrm{end}}\end{cases} | (6) |
公式(6)解释了延迟规则具体的符号替代过程. 其中tend采用公式(5)替代,tend替代后即为dj. 当前时间t经过生长时间间隔Δt后,如果大于dj或者tend,就会产生新分支B,记为Bnew. 该分支Bnew是B的第j+1个分支,并且Bnew开始调用生长规则G开始生长. B(1)表示Bnew会产生第1个分支.
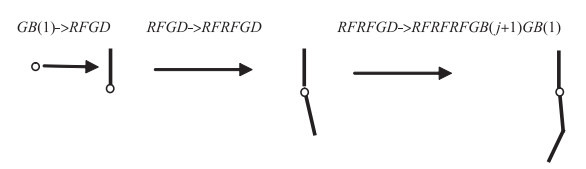
采用生长规则G和分支规则B植物即可以进行生长和分支. 设置初始状态为GB(j), 其中j值可以设置为1,可以表示单根或者初始分支.假设根系初始状态为GB(1), 过程GB(1)->RFGD->RFRFGD->RFRFRFGB(j+1)GB(1)展示了经过3次此迭代后的字符串,该过程可视化过程见图 4.
|
图 4 根系分支可视化过程 Fig.4 Visualization of root branching |
其中可视化过程中G、D、B、R等符号没有对应的可视化图形,F对应某种可视化图形(比如线段). GB(1)表示一个新的种子或者初始分支(图 4中的小圆圈),经过第1次生长,GB(1)变为RFGD,可视化时依据符号R包含的夹角θ和径向角γ取值,从而可视化展示根段F. 经过3次生长,GB(1)变为RFRFRFGB(j+1)GB(1),其中RFRFRF表示该单根或者分支有3个根段,GB(j+1)表示该单根会继续生长,并产生第j+1个分支.
2 结果 2.1 凤眼莲根系动态生长模型构建凤眼莲根系较为独特,它可以看做所有一级根系都生长在一个生长点上(图 5A). 生长末期的凤眼莲的一级根系数量超过100个,每一个单独的一级根系都有且只有一条主根,在主根上密生非常多的二级根系(图 5A). 基于凤眼莲单独一条一级根系实际生长状况,设置在根系生长周期内,每间隔3 d产生一个分支级数0的主根,以此建立凤眼莲根系模型. 首先建立凤眼莲单独一条一级根系的模型(图 6A). 通过对单独一条一级根系立体结构的模拟,再组合成整个植株的根系结构,从而真实模拟凤眼莲生长过程. 凤眼莲只需12 d即可扩张一倍的种群,在本研究中对凤眼莲进行30天的生长模拟,在野外这段时间足够凤眼莲完成生长过程.

|
图 5 凤眼莲扫描整体根系(A)和根系模型构建(B) Fig.5 The scanned whole root system (A) and root model construction (B) of Eichhornia crassipes |
凤眼莲单独一条一级根系的构成主要由分支级数为0的主根和密生的分支级数为1的根毛构成,其中根毛不再产生分支(图 6A). 依据1.2基于L系统的根系动态生长模型构建方法,测量凤眼莲根系单根长度、分支间距、顶端不分支区域、末端不分支区域和分支数目等参数(表 1),可以建立凤眼莲单独一条根系的模型(图 6B).
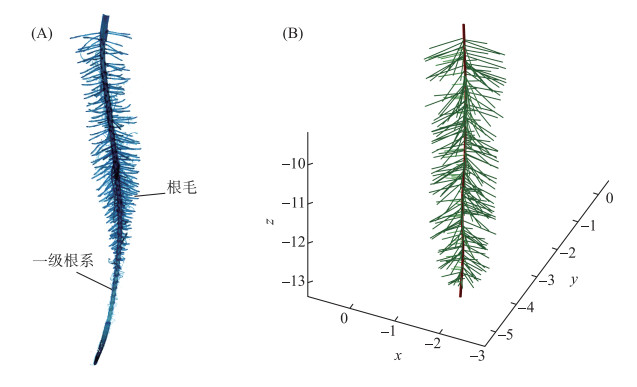
|
图 6 凤眼莲单独一条扫描一级根系(A)和模型构建(B) Fig.6 The scanned lateral root system (A) and root model construction (B) of Eichhornia crassipes |
| 表 1 凤眼莲单独一条一级根系模型参数 Tab. 1 Root parameters of a lateral root system of Eichhornia crassipes |
根据凤眼莲初始和成熟根系指标(表 2)可建立凤眼莲L系统根系动态生长模型. 通过模型构建可以计算出在一个成熟的凤眼莲根系总根毛长度为2022.54 m(根毛长度×根毛个数a×一级根系个数),加上凤眼莲一级根系主根长度20.24 m(主根长度×一级根系个数c),一株凤眼莲成熟根系的总长度可达到惊人的2042.78 m.
| 表 2 凤眼莲整株初生和成熟根系指标 Tab. 2 Root parameters of primary and mature root systems of Eichhornia crassipes |
穗状狐尾藻的根系有以下特征:具有健壮发达的一级根系,而每一个一级根系上二级根系不发达(如图 7A). 其初生根系平均有26.2个一级根系,平均长度为32.31 mm(表 3). 初生根系的一级根系平均有3个分支,分支间平均距离为10.77 mm. 成熟穗状狐尾藻根系的二级根系只有11个左右,平均距离12.09 mm. 据此可以计算出穗状狐尾藻成熟根系的总长度为73.08 m(一级根系长度×一级根系个数c+二级根系长度×二级根系个数a×一级根系个数).
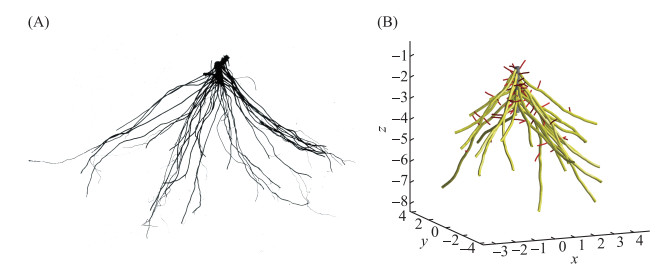
|
图 7 穗状狐尾藻(A)扫描整体根系和(B)根系模型构建 Fig.7 Scanned whole root system (A) and root model construction (B) of Myriophyllum spicatum |
| 表 3 穗状狐尾藻整株初生和成熟根系指标 Tab. 3 Root parameters of primary and mature root systems of Myriophyllum spicatum |
依据获取的穗状狐尾藻根系生长数据,设置基于L系统的穗状狐尾藻根系生长模型参数(表 4),从而较真实地模拟穗状狐尾藻生长过程(图 7B). 对穗状狐尾藻进行了90 d的生长模拟,在实践中足够穗状狐尾藻完成生长过程.
| 表 4 穗状狐尾藻根系生长模型参数 Tab. 4 Root growth model parameters of Myriophyllum spicatum |
在传统L系统进行根系模型构建时,对于不同种类植物的根系,需要依据该根系具体的生长数据进行统计描述,定义特定的生长表达式,从而描述根系生长发育过程[44-45]. 这种方法虽然可以在根系模拟上达到较高的精度,但限制了根系模型的推广,普适性较差. 本文针对水生植物根系生长发育过程的2个重要过程(伸长和分支过程)进行根系动态生长模型构建,不涉及植物根系生长具体过程,而是根系数据进行参数输入,从而使L系统描述根系时具备通用属性. 首先,针对不同类型的植物根系,只需要改变不同分支级数根系的伸长和分支参数,就可以实现特定根系生长发育过程的模拟. 其次,可以通过参数FΔl简单调整,从而实现根系生长更加自然. 如依据公式(1)计算出经过Δt时间的根长增量Δl后,可以定义分辨率Δd(Δd远小于Δl),根段Δl按照分辨率Δd进行分割,即把Δl分割成更小的根段,从而在较高分辨率下实现根系生长发育的可视化,从而使根系生长更加自然. 最后,本文的L系统模型,可以很容易与其他环境模型融合,从而模拟环境影响下的根系生长发育. 比如在模拟营养元素分布对根系生长发育影响时,仅需改变根系伸长和分支的生长角度以及Δl取值即可.
与其他基于L系统的植物模型相比,如杨旨窈和刘骥[46]设计了一种基于L系统的植物生长模拟方法,但缺乏对于植物根系的模拟. 曹红飞和李云飞[20]定义了一种水生植物的生成方法,但其方法只是对已完成生长的水生植物进行,不涉及植物的动态生长过程. 杨乐等[12, 47]采用微分L系统,通过定义水稻不定根、1级枝根和2级枝根系的生长表达式,采用微分形式的根系生长函数来描述水稻根系各生长要素(如根长)在自然生长条件下随时间变化而产生的连续变化的过程. 其优势是根系生长函数是微分方程,可以通过控制dt的粒度(大小)来控制根系的生长. dt粒度小,则根系生长进程的连续性展示较好,但仿真花费时间多;dt粒度大,则根系生长进程的连续性展示较为粗略. 在本文中根系生长函数采用公式(1)(指数函数形式)定义,此外通过定义不同分支级数根系的伸长和分支规则来描述植物各生长要素(在本文中主要指根长)在自然生长条件下随时间变化而产生的连续变化的过程. 这种方式相对于杨乐等[12, 47]的微分方程控制dt来说,本研究的时间粒度Δt可以设置为较大间隔(如1天),在根系生长周期内,在保证高分辨率和准确性的前提下,可以有效地减少迭代次数,实现起来更加简单,计算量更小. 因此不管是针对凤眼莲根系或者是穗状狐尾藻根系,只需要改变伸长、分支规则以及根系生长函数的参数取值就可以实现不同根系的生长过程模拟.
3.2 通过根系动态生长模型探讨水生植物根系对水生生态环境的适应性通过本研究建立了凤眼莲的根系动态生长模型构建,通过模型构建显示凤眼莲可以发展出庞大的根系. 在较为适宜的条件下,植物对资源的竞争能力一般与根系大小和长度呈正比例关系[48]. 由于水生植物根系的吸收作用,会在根系周围形成离子密度低的区域,较高的成熟根系总根长(2042.78 m)有利于凤眼莲占据较多的空间和资源,这表明凤眼莲对富营养化条件有很大的适应性,使得凤眼莲有可能在与本地种竞争中占有优势.
与陆地生态系统相比,湖泊生态系统在环境因子上更加均一和稳定[49-50]. 可以合理推断在湖泊生态系统中的大部分水生植物应该发展出叉状分支构型,如之前针对湖北梁子湖21种水生植物根系构型模型分析发现,水生植物根系整体上呈现叉状分支构型,这可能表明叉状分支构型更适合于营养充足的生境中,这一假设在水生生境中依然适用,也反映了水生植物对水生生境的适应性[41]. 通过本研究的动态生长模型构建可见穗状狐尾藻的总根系长度达73.08 m,但之前的研究发现穗状狐尾藻表现出典型的叉状分支构型[41],表明这种植物对沉水生长环境有较好的适应性.
穗状狐尾藻是中国乡土种,在北美地区为危害较大的入侵种[40, 51]. 较低的适口度、较高的营养获取能力和适应性,以及多样化的繁殖(种子、地下茎和断枝)方式可能促进了其扩散[52-53]. 其能够通过根系和茎吸收营养[54]. 水生植物,尤其是包括沉水植物在内的真性水生植物(euhydrophyte)的根系不发达[55]. 这是由于其根系深埋于水底底质中,与陆生生境相比其环境光照弱、水分饱和、氧含量低、透气性差[56]. 加以水环境中营养元素多溶解于水中,较易被水生植物其他器官组织吸收,水生植物根系吸收营养的功能较为弱化[57]. 随着水体富营养化程度的加重,沉水植物通过茎叶从水体中吸收营养的比例可能会增加,沉水植物无需发展出丰富的根系就足以获得足够的营养,这会导致根系的退化. 根系退化除可能导致根部吸收营养的功能弱化外,还可能降低根系固著能力,这可能是湖泊富营养化导致湖泊沉水植物消亡的部分原因[58]. 穗状狐尾藻作为目前研究较多的水生植物[59],通过根系模型构建建立其根系指标(包括根系生长动态、构型、总根长、总根面积和根系活力等)对富营养化元素的响应,以其为代表探讨水生植物对全球变化的响应是十分必要的.
4 结论本文基于L系统通过定义不同分支级数根系的伸长和分支规则来描述根系各生长要素(主要是根长)在自然生长条件下随时间变化而产生的连续变化过程. 针对不同类型的植物根系,通过根系模型构建不同分支级数的根系伸长和分支参数,来模拟水生植物从初生结构到次生结构,从简单根系到复合根系的动态生长过程. 根系动态生长模型主要包含根系伸长规则和根系分支规则,并包含由主根与侧根的夹角θ和径向角γ确定初始根系生长方向. 特别地,本文建立2种代表水生植物——世界上入侵严重的水生植物凤眼莲和被研究较多的水生植物穗状狐尾藻根系动态生长模型. 采集了凤眼莲和穗状狐尾藻幼苗和成熟植株根系分支数、初始生长速度、不同分支级数根长等特征,之后依据根系生长、分支等规则进行迭代置换,动态地展现了不同时期凤眼莲和穗状狐尾藻根系的生长发育过程. 通过模型构建结果表明凤眼莲较高的成熟根系总根长(2042.78 m)可能有利于其占据较多的空间和资源,使得凤眼莲有可能在竞争中相对本地种占有优势. 本文提出的根系动态生长模型可以很容易和其他环境模型相融合,从而模拟不同环境因子影响下的根系生长发育过程.
致谢: 感谢武汉大学梁子湖湖泊生态系统国家野外科学观测研究站和中国科学院太湖湖泊生态系统研究站提供科研平台.
| [1] |
Waisel Y, Eshel A, Kafkafi U eds. Preface to the third edition. In: Waisel Y, Eshel A, Kafkafi U eds. Plant roots-The hidden half: 3rd ed. New York: CRC Press, 2002: ⅲ.
|
| [2] |
Wang ZQ, Guo DL. Root ecology. Chinese Journal of Plant Ecology, 2008, 32(6): 1213-1216. [王政权, 郭大立. 根系生态学. 植物生态学报, 2008, 32(6): 1213-1216. DOI:10.3773/j.issn.1005-264x.2008.06.001] |
| [3] |
Molles M. Ecology: concepts and applications: fifth edition. New York: McGraw-Hill Education, 2015.
|
| [4] |
Matamala R, Stover DB. Introduction to a Virtual Special Issue: Modeling the hidden half - the root of our problem. New Phytologist, 2013, 200(4): 939-942. DOI:10.1111/nph.12583 |
| [5] |
Grabau LJ. Principles of plant science: Environmental factors and technology in growing plants. Crop Science, 2005, 45(3): 1177. DOI:10.2135/cropsci2005.0003br |
| [6] |
Yan XL, Liao H, Nian H eds. Root biology: Principles and applications. Beijing: Science Press, 2007. [严小龙, 廖红, 年海. 根系生物学: 原理与应用. 北京: 科学出版社, 2007.]
|
| [7] |
Liang Q, Liao H, Yan XL. Quantitative analysis of plant root architecture. Chinese Bulletin of Botany, 2007, 24(6): 695-702. [梁泉, 廖红, 严小龙. 植物根构型的定量分析. 植物学通报, 2007, 24(6): 695-702. DOI:10.3969/j.issn.1674-3466.2007.06.002] |
| [8] |
Yang XL, Zhang XM, Li YL et al. Analysis of root architecture and root adaptive strategy in the Taklimakan desert area of China. Chinese Journal of Plant Ecology, 2008, 32(6): 1268-1276. [杨小林, 张希明, 李义玲等. 塔克拉玛干沙漠腹地3种植物根系构型及其生境适应策略. 植物生态学报, 2008, 32(6): 1268-1276. DOI:10.3773/j.issn.1005-264x.2008.06.007] |
| [9] |
Liao H, Yan XL. Genotypic variation in root morphological characteristics of common bean in relation to phosphorus efficiency. Acta Botanica Sinica, 2001, 43(11): 1161-1166. DOI:10.3321/j.issn:1672-9072.2001.11.011 |
| [10] |
Li SY, Gao JX, Liu J et al. Model virtual root system based on L-systems considering phosphorus. Application Research of Computers, 2014, 31(8): 2380-2382. [李松阳, 高继勋, 刘骥等. 一种考虑磷元素的基于L系统的虚拟根系方法. 计算机应用研究, 2014, 31(8): 2380-2382. DOI:10.3969/j.issn.1001-3695.2014.08.033] |
| [11] |
Peng J, Yang L. Visualization of the rice root growth based on the parametric L system. Journal of Hunan Agricultural University: Natural Sciences, 2020, 46(1): 119-124. [彭军, 杨乐. 基于参数L系统的水稻根系生长可视化研究. 湖南农业大学学报: 自然科学版, 2020, 46(1): 119-124.] |
| [12] |
Yang L. Modeling and visualization of rice root based on L-system. Bulletin of Science and Technology, 2017, 33(5): 156-158. [杨乐. 基于L系统的水稻根系模型构建及可视化研究. 科技通报, 2017, 33(5): 156-158.] |
| [13] |
Fitter AH, Stickland TR, Harvey ML et al. Architectural analysis of plant root systems 1. Architectural correlates of exploitation efficiency. New Phytologist, 1991, 118(3): 375-382. DOI:10.1111/j.1469-8137.1991.tb00018.x |
| [14] |
Bouma TJ, Nielsen KL, van Hal J et al. Root system topology and diameter distribution of species from habitats differing in inundation frequency. Functional Ecology, 2001, 15(3): 360-369. DOI:10.1046/j.1365-2435.2001.00523.x |
| [15] |
Fitter AH. Characteristics and functions of root systems. In: Waisel Y, Eshel A, Kafkafi U eds. Plant roots-The hidden half, 3rd. New York: CRC Press, 2002: 15-32.
|
| [16] |
Oppelt AL, Kurth W, Godbold DL. Topology, scaling relations and Leonardo's rule in root systems from African tree species. Tree Physiology, 2001, 21(2/3): 117-128. DOI:10.1093/treephys/21.2-3.117 |
| [17] |
Berntson GM. Root systems and fractals: How reliable are calculations of fractal dimensions?. Annals of Botany, 1994, 73(3): 281-284. DOI:10.1006/anbo.1994.1033 |
| [18] |
Robinson D, Hodge A, Fitter A. Constraints on the form and function of root systems. In: de Kroon H, Visser EJW eds. Root ecology. Berlin: Springer-Verlag, 2003.
|
| [19] |
Träger S, Wilson SD. Root heterogeneity along an Arctic elevational gradient: The importance of resolution. Functional Ecology, 2017, 31(2): 480-487. DOI:10.1111/1365-2435.12721 |
| [20] |
Cao HF, Li YF. The modeling of one sort of aquatic plant in Taihu Lake. Journal of Suzhou University: Engineering Science Edition, 2011, 31(1): 68-72. [曹红飞, 李云飞. 一种太湖流域水生植物的生成. 苏州大学学报: 工科版, 2011, 31(1): 68-72.] |
| [21] |
Prusinkiewicz P, Lindenmayer A eds. The algorithmic beauty of plants. New York: Springer-Verlag, 2004.
|
| [22] |
Dannowski M, Block A. Fractal geometry and root system structures of heterogeneous plant communities. Plant and Soil, 2005, 272(1/2): 61-76. DOI:10.1007/s11104-004-3981-2 |
| [23] |
Huang XL, Xu X, Liu SL et al. Impact of eutrophication on root morphological and topological performance in free-floating invasive and native plant species. Hydrobiologia, 2019, 836(1): 123-139. DOI:10.1007/s10750-019-3946-3 |
| [24] |
Xie YH, Yu D. The significance of lateral roots in phosphorus (P) acquisition of water hyacinth (Eichhornia crassipes). Aquatic Botany, 2003, 75(4): 311-321. DOI:10.1016/S0304-3770(03)00003-2 |
| [25] |
Xie HM, Li QS, Liu SL et al. Investigation on the status quo of aquatic plant biodiversity in the riverways and littoral zones of the Lake Taihu rim. J Lake Sci, 2020, 32(3): 735-744. [谢洪民, 李启升, 刘帅领等. 环太湖地区河道和湖泊沿岸带水生植物多样性现状调查. 湖泊科学, 2020, 32(3): 735-744. DOI:10.18307/2020.0313] |
| [26] |
Pan X, Villamagna AM, Li B. Eichhornia crassipes Mart. (Solms-Laubach) (water hyacinth). In: Francis RA ed. A handbook of global freshwater invasive species. London and New York: Taylor & Francis Group, 2012: 47-56.
|
| [27] |
Xu RM, Ye WH eds. Biological invasions: Theory and practice. Beijing: Science Press, 2003. [徐汝梅, 叶万辉. 生物入侵: 理论与实践. 北京: 科学出版社, 2003.]
|
| [28] |
You WH, Yu D, Xie D et al. Responses of the invasive aquatic plant water hyacinth to altered nutrient levels under experimental warming in China. Aquatic Botany, 2014, 119: 51-56. DOI:10.1016/j.aquabot.2014.06.004 |
| [29] |
Ismail Z, Othman SZ, Law KH et al. Comparative performance of water hyacinth (Eichhornia crassipes) and water lettuce (Pista stratiotes) in preventing nutrients build-up in municipal wastewater. CLEAN - Soil, Air, Water, 2015, 43(4): 521-531. DOI:10.1002/clen.201200254 |
| [30] |
Eid EM, Shaltout KH. Growth dynamics of water hyacinth (Eichhornia crassipes): A modeling approach. Rendiconti Lincei, 2017, 28(1): 169-181. DOI:10.1007/s12210-016-0589-4 |
| [31] |
Michelan TS, Dainez Filho MS, Thomaz SM. Aquatic macrophyte mats as dispersers of one invasive plant species. Brazilian Journal of Biology, 2017, 78(1): 169-171. DOI:10.1590/1519-6984.06216 |
| [32] |
Teng QM, Sun YJ, Shen YY et al. Growth and phenotypic plasticity variability of Eichhornia crassipes in response to different eutrophic water in Karst wetland. J Lake Sci, 2021, 33(1): 123-137. [滕秋梅, 孙英杰, 沈育伊等. 喀斯特湿地水葫芦(Eichhornia crassipes)生长及表型可塑性特征对不同富营养化水体的响应. 湖泊科学, 2021, 33(1): 123-137. DOI:10.18307/2021.0115] |
| [33] |
Lorber MN, Mishoe JW, Reddy PR. Modeling and analysis of waterhyacinth biomass. Ecological Modelling, 1984, 24(1/2): 61-77. DOI:10.1016/0304-3800(84)90055-3 |
| [34] |
Gamage NPD, Asaeda T. Population dynamics of water hyacinth (Eichhornia crassipes). Research Report of the Research and Education Center for Inlandwater Environment, Shinshu University, 2004, 2: 35-40. |
| [35] |
Yang CH, Everitt JH. Mapping three invasive weeds using airborne hyperspectral imagery. Ecological Informatics, 2010, 5(5): 429-439. DOI:10.1016/j.ecoinf.2010.03.002 |
| [36] |
Wilson JR, Holst N, Rees M. Determinants and patterns of population growth in water hyacinth. Aquatic Botany, 2005, 81(1): 51-67. DOI:10.1016/j.aquabot.2004.11.002 |
| [37] |
Buller LS, Bergier I, Ortega E et al. Dynamic emergy valuation of water hyacinth biomass in wetlands: An ecological approach. Journal of Cleaner Production, 2013, 54: 177-187. DOI:10.1016/j.jclepro.2013.05.006 |
| [38] |
Xie D, Yu D, You WH et al. Morphological and physiological responses to sediment nutrients in the submerged macrophyte Myriophyllum spicatum. Wetlands, 2013, 33(6): 1095-1102. DOI:10.1007/s13157-013-0465-2 |
| [39] |
Son D, Cho KH, Lee EJ. The potential habitats of two submerged macrophytes, Myriophyllum spicatum and Hydrilla verticillata in the river ecosystems, South Korea. Knowledge & Management of Aquatic Ecosystems, 2017, 418: 58. DOI:10.1051/kmae/2017044 |
| [40] |
Smith S, Küpper FC, Trinder C et al. Assessing watermilfoil invasion effects on native macrophyte communities in North American lakes using a novel approach for macrophyte sampling. Knowledge & Management of Aquatic Ecosystems, 2021, 422: 1. DOI:10.1051/kmae/2020043 |
| [41] |
Huang XL, Wang LG, Guan X et al. The root structures of 21 aquatic plants in a macrophyte-dominated lake in China. Journal of Plant Ecology, 2017, 11(1): 39-46. DOI:10.1093/jpe/rtx018 |
| [42] |
Huang XL, Shen N, Guan X et al. Root morphological and structural comparisons of introduced and native aquatic plant species in multiple substrates. Aquatic Ecology, 2018, 52(1): 65-76. DOI:10.1007/s10452-017-9645-0 |
| [43] |
Bouma TJ, Nielsen KL, Koutstaal B. Sample preparation and scanning protocol for computerised analysis of root length and diameter. Plant and Soil, 2000, 218(1/2): 185-196. |
| [44] |
Schnepf A, Leitner D, Landl M et al. CRootBox: a structural-functional modelling framework for root systems. Annals of Botany, 2018, 121(5): 1033-1053. DOI:10.1093/aob/mcx221 |
| [45] |
Leitner D, Klepsch S, Bodner G et al. A dynamic root system growth model based on L-Systems. Plant and Soil, 2010, 332(1/2): 177-192. DOI:10.1007/s11104-010-0284-7 |
| [46] |
Yang ZY, Liu J. Plant growth simulation based on virtual organ L system. Computer Engineering & Software, 2018, 39(10): 182-186. [杨旨窈, 刘骥. 基于虚拟器官L系统的植物生长模拟. 软件, 2018, 39(10): 182-186. DOI:10.3969/j.issn.1003-6970.2018.10.034] |
| [47] |
Yang L, Peng J, Yang HY et al. Three dimensional growth modeling of rice root based on differential L-system. Transactions of the Chinese Society for Agricultural Machinery, 2019, 50(10): 208-214. [杨乐, 彭军, 杨红云等. 基于微分L-系统的水稻根系三维生长模型研究. 农业机械学报, 2019, 50(10): 208-214.] |
| [48] |
Jackson RB, Pockman WT, Hoffmann WA et al. Structure and function of root systems. In: Pugnaire F, Valladares F eds. Functional plant ecology, 2nd. Boca Raton: CRC Press, 2007: 151-173.
|
| [49] |
Niu CJ, Lou AR, Sun RY et al. Foundations in ecology. Beijing: Higher Education Press, 2015. [牛翠娟, 娄安如, 孙儒泳等. 基础生态学. 北京: 高等教育出版社, 2015.]
|
| [50] |
Yang YF, Zhu TC eds. Plant ecology. Beijing: Higher Education Press, 2011. [杨允菲, 祝廷成. 植物生态学. 北京: 高等教育出版社, 2011.]
|
| [51] |
Gassmann A, Cock MJW, Shaw R et al. The potential for biological control of invasive alien aquatic weeds in Europe: A review. Hydrobiologia, 2006, 570(1): 217-222. DOI:10.1007/s10750-006-0182-4 |
| [52] |
Bosch I, Makarewicz JC, Bonk EA et al. Responses of lake macrophyte beds dominated by Eurasian watermilfoil (Myriophyllum spicatum) to best management practices in agricultural sub-watersheds: Declines in biomass but not species dominance. Journal of Great Lakes Research, 2009, 35: 99-108. DOI:10.1016/j.jglr.2009.01.003 |
| [53] |
Huang XL, Yu JL, Liu SL et al. Plant morphological traits and competition index comparisons of three invasive and native submerged plants. Knowledge & Management of Aquatic Ecosystems, 2021, 46(422): 11. DOI:10.1051/kmae/2021012 |
| [54] |
Richter D, Gross EM. Chara can outcompete Myriophyllum under low phosphorus supply. Aquatic Sciences, 2013, 75(3): 457-467. DOI:10.1007/s00027-013-0292-9 |
| [55] |
Kautsky L. Life-cycles of three populations of Potamogeton pectinatus L. at different degrees of wave exposure in the Askö area, Northern Baltic proper. Aquatic Botany, 1987, 27(2): 177-186. DOI:10.1016/0304-3770(87)90065-9 |
| [56] |
Santamaría L. Why are most aquatic plants widely distributed? Dispersal, clonal growth and small-scale heterogeneity in a stressful environment. Acta Oecologica, 2002, 23(3): 137-154. DOI:10.1016/S1146-609X(02)01146-3 |
| [57] |
Ren MX, Wu ZB. Redundancy of plant and it's ecological significance I. studies on growth redundancy of aquatic macrophyte. Acta Ecologica Sinica, 2001, 21(7): 1072-1078. [任明迅, 吴振斌. 植物的冗余及其生态学意义I.大型水生植物生长冗余研究. 生态学报, 2001, 21(7): 1072-1078. DOI:10.3321/j.issn:1000-0933.2001.07.005] |
| [58] |
Sand-Jensen K, Møller CL. Reduced root anchorage of freshwater plants in sandy sediments enriched with fine organic matter. Freshwater Biology, 2014, 59(3): 427-437. DOI:10.1111/fwb.12275 |
| [59] |
Dalla VA, Villa P, Bolpagni R. Functional traits in macrophyte studies: Current trends and future research agenda. Aquatic Botany, 2020, 167: 103290. DOI:10.1016/j.aquabot.2020.103290 |
 2022, Vol. 34
2022, Vol. 34 


