(2: 中国科学院重庆绿色智能技术研究院, 中国科学院水库水环境重点实验室, 重庆 400714)
(3: 重庆邮电大学计算机科学与技术学院, 重庆 400065)
(4: 重庆第二师范学院人工智能学院, 重庆 400065)
(2: Chongqing Institute of Green and Intelligent Technology, Chinese Academy of Sciences, CAS Key Lab on Reservoir Environment, Chongqing 400714, P. R. China)
(3: College of Computer Science and Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, P. R. China)
(4: School of Artificial Intelligence, Chongqing University of Education, Chongqing 400065, P. R. China)
三峡蓄水成库后,库区部分支流受长江干流回水顶托,形成支流库湾;随着水位提升,水体滞留时间延长,加之支流营养物汇集,为浮游藻类生长创造了良好的条件,因而以藻类水华暴发为代表的水环境问题,引起了国内外的普遍广泛关注[1-2]。目前,围绕着三峡水库水华的前期研究揭示:相对充足营养盐供给为水华暴发提供了物质基础,使得特定时期气象、水文条件成为影响藻类生物量变化的主要环境因子[3-6]。但由于水库调蓄引起的复杂水动力条件与其它影响因素的相互拼缀,致使经典意义上环境因子与水华“驱动-响应”关系更趋于复杂。
目前,此方面相关研究大多属于“黑箱”模式,即通过有限样点的监测去构建环境要素与浮游植物间的统计学关系,而对生态系统内在动力学过程认知还存在一定局限性。故而,如何利用长时间序列监测重构出变量间的因果关联成为研究的热点问题,已有多种因果推断方法被开发及应用在生态学问题中,包括格兰杰因果(GC)检验[7]、传递熵(TE)方法[8]、PC算法[9]、收敛交叉映射(CCM)算法[10]。其中CCM算法是立足于非线性确定性动力学系统时间序列重构(Takens定理)[11]的基础上,通过重构吸引子获取变量的历史信息,随着时间序列不断增长最终保持收敛而判断因果关系的存在。最近,非线性时序分析方法开始应用在分析水域生态系统中复杂的因果关系上,如Chang等[12]量化了浮游植物多样性、生物量与环境因子间的因果关系, 叶麟等[13]研究了三峡水库水位波动与香溪河高频监测藻类的因果关联。
澎溪河(小江)是三峡水库中消落带面积最大的一条支流,其中高阳平湖是水华研究关注度较高的区域。近些年,为治理水库水位落差(145~175 m)所产生的消落带, 澎溪河上修建了调节坝进行水位拦蓄[14],形成水面积达14.8 km2人工湖——汉丰湖,显著延长上游水体的水力滞留时间,驱使水体由河流形态转变为兼具湖泊-河流特征的特殊形态[15-16]。本文选取了高阳平湖与汉丰湖监测数据进行分析,运用非线性时间序列分析框架量化浮游植物生物量与环境因子的因果关系,旨在阐明三峡库区支流水华的潜在驱动因子,为筑坝河流水体富营养化及水华暴发的生态风险防控提供科学依据。
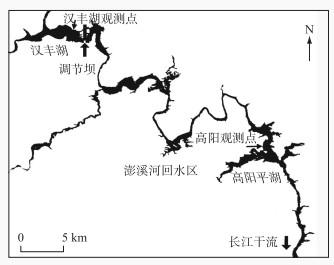
1 材料与方法 1.1 研究区域概况本项目选取澎溪河中高阳平湖和汉丰湖2个点位开展研究(图 1)。澎溪河流域位于三峡水库中段北岸,属于亚热带湿润季风气候,其流域面积5172 km2,其中消落带总面积高达56.60 km2,属于库区消落带面积最大的支流。根据前期的观测,这两个区域的水生态系统对三峡大坝和汉丰湖调节坝运行响应敏感,因而开展浮游植物响应生境变化研究具有一定的典型性。
|
图 1 澎溪河研究区域采样点位置 Fig.1 Location of sampling sites in the study area of Pengxi River |
研究选取2007年6月到2018年9月三峡高阳平湖(GY)和汉丰湖(HF)观测点的月频率人工时序数据。模型构建候选变量包括气温(AT)、降雨量(Rain)、日照时数(Sunshine hours)、风速(Wind speed)、水温(WT)、流量(Q)、三峡大坝水位(WLTGR)、汉丰湖水位(WLHF)、总氮(TN)、总磷(TP)、叶绿素a (Chl.a)。其中气象数据来源于中国气象数据网(http://data.cma.cn/),三峡大坝水位数据来源于中国长江三峡集团公司水情信息网发布的三峡上游水位信息(http://www.ctg.com.cn/inc/sqsk.php),汉丰湖大坝水位数据来源于重庆市开州区汉丰湖管理委员会,研究团队前期对澎溪河流域水温、流量、总氮、总磷和叶绿素a变化进行了长期的观测,总氮和总磷浓度测定分别参考碱性过硫酸钾消解紫外分光光度法(GB 11894—1989)和过硫酸钾消解钼酸铵分光光度法(GB 11893—1989),叶绿素a浓度测定参考丙酮提取分光光度法(HJ 897—2017)。
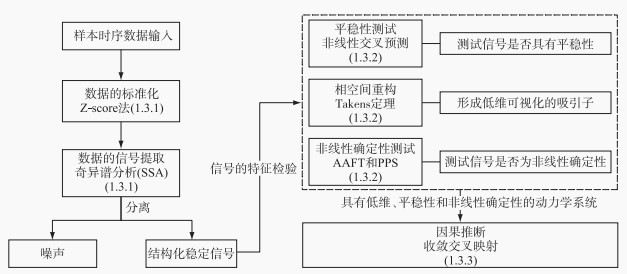
1.3 非线性时间序列分析方法本研究采用的非线性时间序列分析方法流程框架如图 2所示。首先对每个时序数据进行标准化处理以消除量纲的影响,其次再对标准化后的数据进行奇异谱分析以分离出结构化稳定信号和噪声,然后将保留的结构化稳定信号分别进行平稳性测试、相空间重构、信号非线性确定性测试,最后对满足条件的信号用作基于收敛交叉映射的因果推断方法。
|
图 2 非线性时间序列分析方法流程图 Fig.2 Flow chart of nonlinear time-series analysis |
① 数据的标准化
为了消除量纲的影响,本文对所有样本时序数据按照式(1)进行Z-score标准化法处理。
| ˆX=X−μσ | (1) |
式中,X和
② 数据的信号提取
野外的监测数据可能是不稳定且有噪声的。为了将每个样本时间序列中的结构化稳定信号从非结构化噪声中分离出来,本研究应用了奇异谱分析(SSA)方法[17-21],SSA是一种经典的分解与重构时间序列数据的方法,分解有如下几个步骤:轨迹矩阵的构建、奇异值分解、分组和重构。
轨迹矩阵的构建:首先将长度为N的样本时间序列数据[X1, X2, …, XN]以合适的窗口长度L进行滞后排列处理,得到一个L行的N-L+1的轨迹矩阵Y。
| Y=[x1x2⋯xkx2x3⋯xk+1⋮⋮⋱⋮xLxL+1⋯xN] | (2) |
奇异值分解(singular value decomposition, SVD):通过计算YYT将轨迹矩阵Y进行奇异值分解,得到L个特征值, 按照降序排列为λ1, λ2, …, λL, 对应的特征向量为U1, U2, …, UL, 则轨迹矩阵Y可以写作:
| Y=E1+E2+⋯+Ed | (3) |
式中,d=rank(Y)为Y的非零奇异值的个数,
分组:将式(3)中的矩阵Ei划分为k个不相交的子集m1, m2, …, mk, 设m={i1, i2, …, iL}, 则合成后的矩阵为Ym=Yi1, Yi2, …, YiL, 计算m={i1, i2, …, iL}的每个合成矩阵,则式(3)可以写作:
| Y=Ym1+Ym2+⋯+Ymk | (4) |
重构:将式(4)得到的每个合成矩阵通过对角平均计算公式转化为时间序列。公式如下:
| Zk={1kk∑m=1Z∗m,k−m+11⩽k⩽L∗1L∗k∑m=1Z∗m,k−m+1L∗<k<K∗1N−k+1N−K∗+1∑m=k−K∗+1Z∗m,k−m+1K∗<k⩽N | (5) |
式中,Z是一个L×K的矩阵,元素为Zij(1≤i≤L, 1≤j≤k), L*=min(L, K); K*=max(L, K), N=L+K-1。
本研究用时间序列的潜在低维确定性分量来表示每个信号,用信号强度来衡量信号解释的方差。每个信号可能由振荡成分(如年周期)和非线性或线性趋势组成。相比之下,噪声可能由观测误差、潜在的高维或随机过程以及由外生强迫造成的极值组成[22]。
1.3.2 信号的特征检验① 信号的平稳性检验
本研究对每个信号进行了平稳性实验,目的是检测每个信号在整个时间序列中是否表现出相似的动态行为,若满足可合理地认为信号是来自一个单一的平稳动态系统[23]。正如Kadlec和Wallace所建议,起始时期的状态并不是推断长时期动态的可靠依据[24]。
观测过程中相对不变的统计矩(方差和均值)反映了线性时间序列分析的弱平稳性。然而,这种方法在非线性时间序列系统中是不可行的。即使底层的动态结构没有改变,也可能出现一些突变的时间节点。因此,为了测试突变点(即动态行为发生变化的时间段),本研究使用了非线性交叉预测算法[23]。每个信号将被分成3个不重叠的片段,用Nash-Sutcliffe效率(Nash-Sutcliffe efficiency, NSE)来评估每对片段之间的预测能力[25],将最小阈值设置为NSE≥0.65[26]。
② 信号的相空间重构
我们采用时滞嵌入的方法对各个稳定信号的相空间进行重构,使重构后的系统动力学可视化。相空间中的每一点都表示唯一的系统状态,其轨迹被用来描述系统随着时间序列的演化[27]。该轨迹会形成一个具有明显视觉规律的几何图形——吸引子。在耗散系统中,吸引子通常占据一个低维子空间,因此,无论系统的实际维度如何,一般利用较少的变量来进行分析和建模长期的系统动力学。
我们通过嵌入一个单独的时间序列来重建系统的真正吸引子。根据Takens定理,通过嵌入了足够的维数来包含原始的吸引子,重构的吸引子将与真实的吸引子一一映射[11]。每次时间嵌入都需要指定的嵌入时延d和相应的嵌入维数m,我们将嵌入维数m设为m-1。通常情况下,交互信息函数中的第一个局部最小值被指定为嵌入时延[28],最近邻测试被用来确定最低的嵌入维数。
③ 信号的非线性确定性测试
由于线性随机过程,重构的吸引子可能表现出几何规律。为了区分这种情况,我们使用替代数据测试来防止意外的几何规则被误认为非线性确定性结构[29-31]。
替代数据检验基于检验零假设,即重构的吸引子是线性随机的[32]。替代数据将破坏原始信号的一些时间结构,但同时保留相关的统计属性。因此,我们可以在线性随机过程中检验重构吸引子表观的规律性,以确定原假设是否被拒绝。对于每个重构的吸引子,生成两组代理数据向量: 首先,利用振幅傅里叶变换(AAFT)保存信号的概率分布和功率谱,并检测非线性是否反映了潜在线性高斯过程观测函数中的明显非线性结构[29]; 然后,使用伪周期代理体(PPS)保持大尺度周期行为的同时破坏细尺度序列结构,用于测试重构的吸引子反映的是轨迹上的随机变化,而不是确定性的非线性过程[33]。
接下来,比较每个重构吸引子及其替代数据中的非线性结构的特征: 首先,我们将重构吸引子中的点进行短期预测,用于度量确定性结构[34]; 其次,利用排列熵[35]计算时间序列中的信息。低熵意味着可以从过去的值预测观测结果(零熵意味着可以从过去的值完美地预测观测结果),这是确定性的。相反,最大熵意味着观测结果是独立且同分布的。非线性确定性动力学与高性能预测测试和低排列熵相一致。因此,我们使用上尾检验(非线性预测)和下尾检验(排列熵)进行实验。
使用非参数秩序统计量[30]来验证AAFT和PPS的假设检验。设每个单尾测试生成(k/α)-1=399个代理,其中假阳性α的概率设为0.05,测试的灵敏度设为k=20。如果重构吸引子和代理吸引子中提取的统计量都在极端范围内(上尾检验和下尾检验的K最大值和最小值),则零假设将被拒绝。最后,我们可以得出结论,通过拒绝零假设证明了低维和非线性确定性动力学结构,这为后续使用CCM算法提供了先决条件。
1.3.3 非线性时序的因果推断① 收敛交叉映射(CCM)算法
本研究采用CCM算法进行变量间的因果判断。该方法基于Takens定理,通过重构时间序列中的动态信息,将每个时间序列中重构的吸引子一一映射到真实的系统吸引子[11]。换句话说,时间序列变量在同一个动态系统中是相互关联的,因此,相应的变量会有因果关系[10, 36]。
基于最近邻预测算法,利用CCM确定两个重构吸引子之间的几何关系: 驱动变量的信号值由响应变量信号重构吸引子上的点集预测。随着时间序列的增加,交叉映射值逐渐收敛到0到1之间,这为变量之间的因果关系提供了证据[10]。
② CCM结果的显著性检验
研究采用Ebisuzaki替代数据测试来对变量间因果关系进行显著性检验,其原理是在分析过程中保留了原始信号的功率谱,但随机化了分量频率的相位,从中可筛选出由协变量信号同相而导致的假阳性[37]。依据前人研究的参数设置[38],本研究将交叉映射值与k=500的替换数据获得的交叉映射值进行比较,并设置显著性水平P=0.05,P值计算为(n+1)/(k+1),其中n为预测效果优于重构吸引子的替代数量,CCM测试程序将100次重复的CCM测试结果的平均值作为最终结果。
1.4 分析方法间的比较研究将非线性时序分析(CCM算法)结果与两种线性分析方法(相关性分析与格兰杰因果检验)进行比较。其中,相关性分析采用皮尔森(Pearson)相关系数来衡量,其定义为两个变量之间的协方差和标准差的商,其值范围在-1到1之间。假定两个变量为X和Y,它们之间的相关系数用r表示,其公式为:
| r=n∑i=1(Xi−ˉX)(Yi−ˉY)√∑ni=1(Xi−ˉX)2√∑ni=1(Yi−ˉY)2 | (6) |
格兰杰因果检验是一种假设检验的统计方法,检验一组时间序列X是否为另一组时间Y的格兰杰原因。简单来说,通过构建一个计量模型来预测时间序列Y, 此时如果将时间序列X从此模型中移除,该模型对Y的预测能力下降了,那么此时可以认为X是Y的格兰杰原因。我们利用格兰杰因果检验方法来衡量叶绿素a与其它样本变量之间的因果关系。格兰杰因果检验的前提是需要进行单位根检验以验证时间序列是否为平稳序列。若为非平稳序列,则需要进行协整检验,当时序数据存在协整关系时,可以进行格兰杰因果检验,否则为“伪回归”。
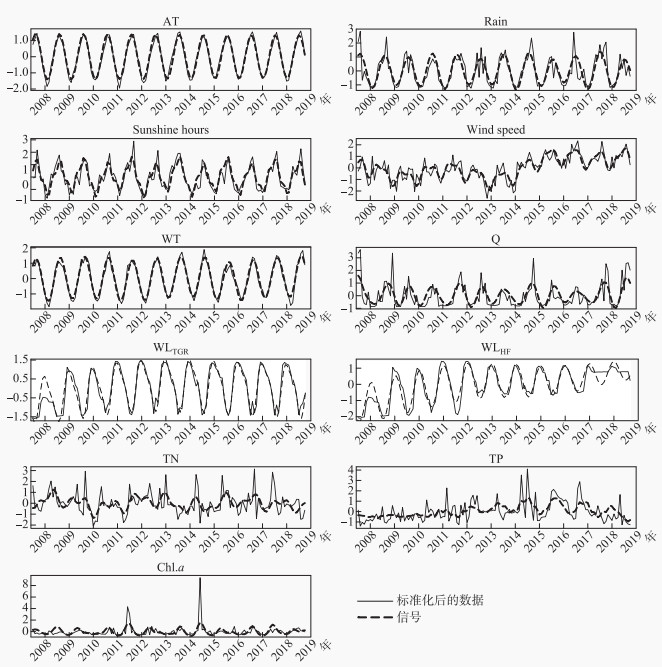
2 结果与讨论 2.1 叶绿素a与环境因子观测数据的非线性动力学重建研究首先对收集到的观测数据进行预处理,包括观测变量标准化和信噪分离。这是由于野外的观测数据会受各种不确定因素的影响,因此数据信噪分离对于后续研究非线性因果关系是必要的。本文利用奇异谱分析(SSA)从观测数据中分离潜在的稳定信号、缓慢变化的趋势、振荡和噪声。以2007年6月到2018年9月高阳平湖观测数据为例,每个观测变量都被进行了信号的提取(图 3)。根据表 1,对于气象水文数据,可以提取出较强的信号部分,如提取的气温、水温、三峡大坝水位、汉丰湖调节坝水位等信号可以解释95.54 %、95.04 %、95.04 % 和83.52 % 的观测方差。而相比较下,由于营养盐与藻类指标在长时间序列上波动性,导致从观测数据中提取的信号占比相对较低,如总氮、总磷以及叶绿素a的信号占比分别为30.08 %、36.43 % 和26.43 %。然而,信号强弱并不能直接影响分析变量间关系的结果,本研究中假设提取的信号能够通过后续的平稳性、非线性确定性测试,仍被认为是能进行非线性因果建模分析。因此,对于诸如淡水生态系统等一些复杂系统产生的时间序列观测数据来讲,对数据进行一些预处理将更有助于去识别系统内部变化产生的潜在因果关系。
|
图 3 高阳平湖主要变量的结构变化 Fig.3 Structure variation of the main variables in Lake Gaoyangping |
| 表 1 高阳平湖观测点平稳性、低维和非线性确定性动力学的证据 Tab. 1 Evidence for stationary, low-dimensional and non-linear deterministic dynamics in Lake Gaoyangping |
本研究首先采用非线性交叉预测算法,来证明观测变量提取的信号满足平稳性假设。若计算的NSE值高于阈值(0.65)[26],则表明,可变信号的基本动态结构在其他环境条件的影响下保持稳定。以高阳平湖监测数据为例,除了风速和总磷的信号预测能力低于阈值,分别为0.51和-0.18,其余所有变量信号均通过了平稳性和非线性确定性测试(表 1)。
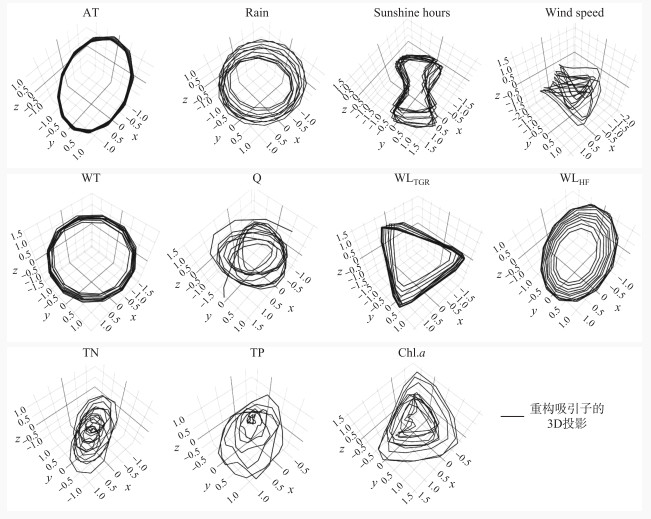
其次,研究利用相空间重构的方法计算信号的嵌入时间维度。利用Takens定理,将每个提取的信号重构吸引子,结果表明变量信号的嵌入维数(m)维持在3~5之间,且多以环状为特征(图 4)。因此证明了研究的水生态系统满足低维动力学特征。
|
图 4 高阳平湖观测点各个信号的相空间重构 Fig.4 Phase space reconstruction of each signal in Lake Gaoyangping |
最后,为证明提取的信号满足非线性确定性假设,运用AAFT和PPS替代测试方法。对于每个观测变量得到的信号,使用非线性预测和排列熵2种不同的替代方法分别进行2次测试。如果每对测试中至少有一个被拒绝,则可以拒绝重构吸引子的零假设(表 1)。基于该标准,除了高阳平湖观测点的总磷以外,其余所有信号都可以拒绝重构吸引子的线性随机动力学的零假设。从以上结果可以看出,自然系统是非线性且多样化的,而非线性模型框架是阐释浮游植物与环境因素关系重要手段。
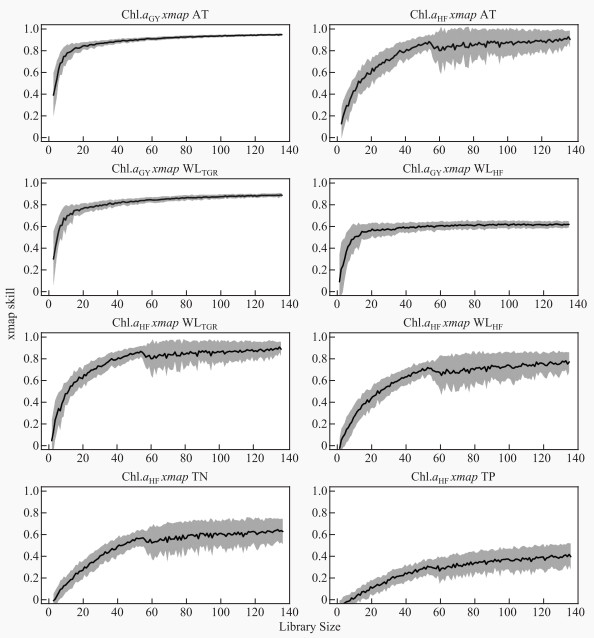
2.2 环境因子与叶绿素a间非线性因果关系的建立对通过上述测试的变量,研究运用收敛交叉映射算法(CCM)来测试每个环境因子与叶绿素a之间的因果关系。如图 5所示,“Y xmap X”的含义为使用Y相空间中的点集来预测X信号的值,以测试X是否驱动Y,若因果强度值随着时间序列增加最终收敛,则具有因果性。根据表 2高阳平湖营养盐与叶绿素a之间的实验结果中,由于总磷在前面的实验中均未通过平稳性测试和非线性确定性测试,故而不满足CCM实验的先决条件,而总氮与叶绿素a之间的因果关系并不显著(因果强度为-0.480,且P=0.992);水文指标包括水温、三峡大坝水位、汉丰湖调节坝水位、和上游流速与叶绿素a之间的因果强度较高,分别为0.942、0.873、0.612和0.871,表现出明显的收敛性且通过了显著性检验(P=0.002)。相比之下,汉丰湖的总氮和总磷对叶绿素a的因果强度为0.609和0.378,且总磷与叶绿素a的因果关系未通过显著性检验。研究结果也证实支流调节坝修建,显著延长汉丰湖水体的水力滞留时间,使得上游筑坝拦截的水体中营养盐与藻类关系较之下游更为显著,而下游高阳平湖观测点位水动力条件更为复杂,不仅受到三峡大坝蓄水造成的干流回水顶托影响,也受到支流调节坝运行的影响,因而此区域浮游植物与营养盐关系较为复杂,也值得更为深入的科学研究[39]。此外,汉丰湖中总氮较之于总磷对叶绿素a变化影响更为显著,这是由于人工调蓄造成水体扰动程度较大,导致营养盐浓度的波动也较大,试验初期水体会出现氮限制的情况[40],但随着汉丰湖调节坝调蓄过程的不断运行,可推断出水体磷限制的情况会逐步占据优势。
|
图 5 关键环境变量与叶绿素a的CCM分析结果 Fig.5 CCM results between key environmental variables and Chl.a |
| 表 2 高阳平湖和汉丰湖中关键环境变量与叶绿素a因果关系的比较 Tab. 2 Comparison of causal relationship between key environmental factors and Chl.a based on CCM in Lake Gaoyangping and Lake Hanfeng |
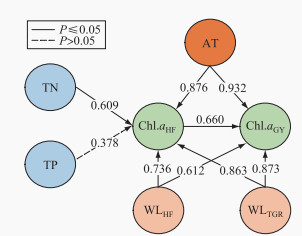
在气象因素中,根据表 3的CCM结果,显示温度、降雨量和日照时数与叶绿素a之间的因果强度分别为0.932、0.904和0.808且都通过了显著性检验(P=0.002), 这表明温度、日照时数和降雨量与叶绿素a有着密切的因果关系,并影响着浮游植物生物量动态,而由于风速未能通过平稳性测试,无法进行CCM分析。研究构建了澎溪河浮游植物响应的因果概化图(图 6),对比发现三峡大坝水位对高阳平湖和汉丰湖的叶绿素a的因果强度较高,分别为0.873和0.863且都通过了显著性检验(P=0.002),而汉丰湖调节坝水位变化对汉丰湖叶绿素a影响高于下游澎溪河。这一发现也为利用水位调控控制水华暴发提供了相关科学依据。
| 表 3 不同方法下环境因子与叶绿素a间的因果关系比较 Tab. 3 Comparison of the response of the Chl.a to environmental factors under different causality methods |
|
图 6 澎溪河叶绿素a与环境因子的因果网络图 Fig.6 Causal network diagram between environmental factors and Chl.a in Pengxi River |
从观测时间序列数据中识别因果关系及其强度对于复杂的生态动力学系统至关重要[41]。研究证实,收敛交叉映射(CCM)比相关性分析与格兰杰因果检验更适用于浮游植物驱动因子的研究。根据表 3所示,利用非线性CCM分析方法建立起的环境因子与叶绿素a之间的因果强度,远大于相关系数计算结果,这正好说明与传统的相关性分析相比,基于非线性CCM分析方法能较为有效识别出变量间的关系。同时,从格兰杰因果检验的结果显示,只有日照时数和上游流速是影响叶绿素a变化的关键变量,而CCM并未准确识别出总磷对叶绿素a的因果关系,但它却是叶绿素a的格兰杰原因(P=0.002),这意味着基于线性的格兰杰因果推断与非线性因果分析结果可能会存在出入。正如Sugihara等的观点,他们认为格兰杰因果推断最适合于由随机主导的线性系统,并且不适合于建模具有高度非线性和确定性骨架的系统[10]。此外,CCM只是因果关系存在的必要条件,不是充分条件[7]。如果两个时间序列具有双向因果关系,则很难根据替代数据测试明确找到因果关系[42],也表明该领域在直接运用因果模型建立关系时需要更多地考虑一些先验知识进去。
3 结论研究围绕着三峡水库澎溪河流域高阳平湖和汉丰湖获取的长时间监测数据,结合非线性时间序列因果建模分析,探索了该方法在藻类时序变化驱动力解析上的应用,具体结论如下:①奇异谱分析(SSA)能够有效分离叶绿素a及环境因素的低维确定性动力学信号;②基于收敛交叉映射(CCM)的因果分析方法揭示气象因子(气温、降雨、日照)、支流流量、水温、三峡大坝水位和汉丰湖调节坝水位是影响高阳平湖叶绿素a长期变化的重要因素;③总氮、总磷为代表的营养盐只在汉丰湖观测点中表现出与叶绿素a的因果关系,且总氮较之于总磷对叶绿素a的变化影响更为显著;④研究证实非线性时序方法相较于传统的相关性分析与格兰杰因果检验在解析水生态变化驱动力上更具优势。简而言之,本文所探讨的非线性时序因果建模策略,能够有效解析藻类长时序监测的驱动因子,这可为三峡水库水华的防控管理提供科学参考。然而,在实际应用中建议尽可能在目标水域布设多个观测点位,特别是涉及到水位调控系统造成的生境空间异质性现象,不同空间点位可有效克服在藻类空间变化刻画上的局限,增加系统因果发现的稳健性。
| [1] |
Cai QH, Sun ZY. Water environment and aquatic ecosystem of Three Gorges Reservoir, China: Progress and prospects. J Lake Sci, 2012, 24(2): 169-177. [蔡庆华, 孙志禹. 三峡水库水环境与水生态研究的进展与展望. 湖泊科学, 2012, 24(2): 169-177. DOI:10.18307/2012.0201] |
| [2] |
Cai QH, Hu ZY. Studies on eutrophication problem and control strategy in the Three Gorges Reservoir. Acta Hydrobiologica Sinica, 2006, 30(1): 7-11. [蔡庆华, 胡征宇. 三峡水库富营养化问题与对策研究. 水生生物学报, 2006, 30(1): 7-11. DOI:10.3321/j.issn:1000-3207.2006.01.002] |
| [3] |
Li Z, Fang F, Guo JS et al. Spring algal bloom and nutrients characteristics in Xiaojiang River backwater area, Three Gorge Reservoir, 2007. J Lake Sci, 2009, 21(1): 36-44. [李哲, 方芳, 郭劲松等. 三峡小江回水区段2007年春季水华与营养盐特征. 湖泊科学, 2009, 21(1): 36-44. DOI:10.18307/2009.0105] |
| [4] |
Cao CJ, Zheng BH, Zhang JL et al. Systematic investigation into winter and spring algal blooms in Daning River of Three Gorges Reservoir. Environmental Science, 2009, 30(12): 3471-3480. [曹承进, 郑丙辉, 张佳磊等. 三峡水库支流大宁河冬、春季水华调查研究. 环境科学, 2009, 30(12): 3471-3480. DOI:10.13227/j.hjkx.2009.12.005] |
| [5] |
Yang M, Zhang S, Hu ZY. Characteristics and preliminary regulating factors of cyanobacterial bloom in Xiangxi Bay of the Three Gorges Reservoir. J Lake Sci, 2014, 26(3): 371-378. [杨敏, 张晟, 胡征宇. 三峡水库香溪河库湾蓝藻水华暴发特性及成因探析. 湖泊科学, 2014, 26(3): 371-378. DOI:10.18307/2014.0306] |
| [6] |
Huang YL, Chen MX, Liu DF et al. Effect of nitrogen, phosphor, light and water temperature on the for mation and disappearance of blue-green algae bloom. Journal of Northwest A & F University: Natural Science Edition, 2008, 36(9): 93-100. [黄钰铃, 陈明曦, 刘德富等. 不同氮磷营养及光温条件对蓝藻水华生消的影响. 西北农林科技大学学报: 自然科学版, 2008, 36(9): 93-100.] |
| [7] |
Granger CWJ. Investigating causal relations by econometric models and cross-spectral methods. Econometrica, 1969, 37(3): 424-438. DOI:10.2307/1912791 |
| [8] |
Schreiber T. Measuring information transfer. Physical Review Letters, 2000, 85(2): 461-464. DOI:10.1103/PhysRevLett.85.461 |
| [9] |
Spirtes P, Glymour C. An algorithm for fast recovery of sparse causal graphs. Social Science Computer Review, 1991, 9(1): 62-72. DOI:10.1177/089443939100900106 |
| [10] |
Sugihara G, May R, Ye H et al. Detecting causality in complex ecosystems. Science, 2012, 338(6106): 496-500. DOI:10.1126/science.1227079 |
| [11] |
Takens F. Detecting strange attractor in turbulence. In: Rand D, Young LS eds. Dynamical systems and turbulence, Warwick 1980. Berlin: Springer, 1981: 366-381.
|
| [12] |
Chang CW, Miki T, Ye H et al. Causal networks of phytoplankton diversity and biomass are modulated by environmental context. Nature Communications, 2022, 13: 1140. DOI:10.1038/s41467-022-28761-3 |
| [13] |
Ye L, Tan L, Wu XH et al. Nonlinear causal analysis reveals an effective water level regulation approach for phytoplankton blooms controlling in reservoirs. Science of the Total Environment, 2022, 806: 150948. DOI:10.1016/j.scitotenv.2021.150948 |
| [14] |
Zhang H. Analysis of the characteristics and ecosystem service of the water-level-fluctuating zone in the Three Gorges Reservoir. Resources and Environment in the Yangtze Basin, 2008, 17(3): 374-378. [张虹. 三峡重庆库区消落区基本特征与生态功能分析. 长江流域资源与环境, 2008, 17(3): 374-378. DOI:10.3969/j.issn.1004-8227.2008.03.009] |
| [15] |
Yang B, He BH, Wang DB. Hanfeng pre-dam commissioning eutrophication status and control evaluation in Three Gorges Reservoir. Environmental Science, 2016, 37(12): 4586-4595. [杨兵, 何丙辉, 王德宝. 三峡前置库汉丰湖试运行年水体水质现状及控制效果评估. 环境科学, 2016, 37(12): 4586-4595. DOI:10.13227/j.hjkx.201605233] |
| [16] |
付适. 运行期汉丰湖氮磷生态化学计量比与浮游植物群落特征研究[学位论文]. 重庆: 西南大学, 2020.
|
| [17] |
Ghil M, Allen MR, Dettinger MD et al. Advanced spectral methods for climatic time series. Reviews of Geophysics, 2002, 40(1): 3-1. DOI:10.1029/2000rg000092 |
| [18] |
Marques CAF, Ferreira JA, Rocha A et al. Singular spectrum analysis and forecasting of hydrological time series. Physics and Chemistry of the Earth, Parts A/B/C, 2006, 31(18): 1172-1179. DOI:10.1016/j.pce.2006.02.061 |
| [19] |
Golyandina N, Osipov E. The "Caterpillar"-SSA method for analysis of time series with missing values. Journal of Statistical Planning and Inference, 2007, 137(8): 2642-2653. DOI:10.1016/j.jspi.2006.05.014 |
| [20] |
Hassani H. Singular spectrum analysis: Methodology and comparison. Journal of Data Science, 2021, 5(2): 239-257. DOI:10.6339/jds.2007.05(2).396 |
| [21] |
Golyandina N, Nekrutkin V, Zhigljavsky A. Analysis of time series structure. New York: Chapman and Hall/CRC, 2001. DOI:10.1201/9781420035841
|
| [22] |
Regan HM, Colyvan M, Burgman MA. A taxonomy and treatment of uncertainty for ecology and conservation biology. Ecological Applications, 2002, 12(2): 618-628. DOI:10.1890/1051-0761(2002)012[0618:atatou]2.0.co;2 |
| [23] |
Schreiber T. Detecting and analyzing nonstationarity in a time series using nonlinear cross predictions. Physical Review Letters, 1997, 78(5): 843-846. DOI:10.1103/physrevlett.78.843 |
| [24] |
Kadlec RH, Wallace SC. Treatment wetlands (2nd Ed). Boca Raton, FL: CRC Press, 2009.
|
| [25] |
Nash JE. River flow forecasting through conceptual models part Ⅰ-A discussion of principles. Journal of Hydrology, 1970, 10(3): 282-290. DOI:10.1016/0022-1694(70)90255-6 |
| [26] |
Ritter A. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. Journal of Hydrology, 2013, 480: 33-45. DOI:10.1016/j.jhydrol.2012.12.004 |
| [27] |
Nolte DD. The tangled tale of phase space. Physics Today, 2010, 63(4): 33-38. DOI:10.1063/1.3397041 |
| [28] |
Fraser AM, Swinney HL. Independent coordinates for strange attractors from mutual information. Physical Review A, General Physics, 1986, 33(2): 1134-1140. DOI:10.1103/physreva.33.1134 |
| [29] |
Schreiber T. Surrogate time series. Physica D: Nonlinear Phenomena, 2000, 142(3/4): 346-382. DOI:10.1016/S0167-2789(00)00043-9 |
| [30] |
Theiler J. Testing for nonlinearity in time series: The method of surrogate data. Physica D: Nonlinear Phenomena, 1992, 58(1/2/3/4): 77-94. DOI:10.1016/0167-2789(92)90102-S |
| [31] |
Small M, Tse CK. Detecting determinism in time series: The method of surrogate data. IEEE Transactions on Circuits and Systems Ⅰ: Fundamental Theory and Applications, 2003, 50(5): 663-672. DOI:10.1109/TCSI.2003.811020 |
| [32] |
Kantz H, Schreiber T. Nonlinear time series analysis. Cambridge: Cambridge University Press, 2003. DOI:10.1017/cbo9780511755798
|
| [33] |
Small M. Applying the method of surrogate data to cyclic time series. Physica D: Nonlinear Phenomena, 2002, 164(3/4): 187-201. DOI:10.1016/S0167-2789(02)00382-2 |
| [34] |
Kaplan D, Glass L, Berger SA. Understanding nonlinear dynamics. Physics Today, 1996, 49(2): 62. DOI:10.1063/1.2807512 |
| [35] |
Bandt C, Pompe B. Permutation entropy: A natural complexity measure for time series. Physical Review Letters, 2002, 88(17): 174102. DOI:10.1103/PhysRevLett.88.174102 |
| [36] |
Tsonis AA, Deyle ER, Ye H et al. Convergent cross mapping: Theory and an example. Advances in nonlinear geosciences. Cham: Springer International Publishing, 2017: 587-600. DOI:10.1007/978-3-319-58895-7_27
|
| [37] |
Ebisuzaki W. A method to estimate the statistical significance of a correlation when the data are serially correlated. Journal of Climate, 1997, 10(9): 2147-2153. DOI:10.1175/1520-0442(1997)0102147:amtets>2.0.co;2 |
| [38] |
Ye H. Nonlinear tools for a nonlinear world: Applications of empirical dynamic modeling to marine ecosystems. UC San Diego, 2015. |
| [39] |
Ouyang T, Shan K, Zhou BT et al. Research on the online forecasting of algal kinetics based on time-series data and LSTM neural network: Taking Three Gorges Reservoir as an example. J Lake Sci, 2021, 33(4): 1031-1042. [欧阳添, 闪锟, 周博天等. 基于LSTM网络的在线藻类时序数据预测研究: 以三峡水库为例. 湖泊科学, 2021, 33(4): 1031-1042. DOI:10.18307/2021.0406] |
| [40] |
Qin RC, Xiao Y, Guo JS et al. In situ research of relationship between cellular N/P of dominate algae species and limitation evaluation in Pengxi River of the Three Gorges Reservoir. J Lake Sci, 2018, 30(5): 1284-1294. [秦镕聪, 肖艳, 郭劲松等. 三峡库区澎溪河典型优势藻细胞N/P比与限制性评价的原位分析. 湖泊科学, 2018, 30(5): 1284-1294. DOI:10.18307/2018.0511] |
| [41] |
Shan K, Ouyang T, Wang X et al. Temporal prediction of algal parameters in Three Gorges Reservoir based on highly time-resolved monitoring and long short-term memory network. Journal of Hydrology, 2022, 605: 127304. DOI:10.1016/j.jhydrol.2021.127304 |
| [42] |
Bartsev S, Saltykov M, Belolipetsky P et al. Imperfection of the convergent cross-mapping method. IOP Conference Series: Materials Science and Engineering, 2021, 1047(1): 012081. DOI:10.1088/1757-899x/1047/1/012081 |
 2023, Vol. 35
2023, Vol. 35 


