(2: 华中科技大学网络空间安全学院, 武汉 430074)
(3: 武汉四像科技有限公司, 武汉 430074)
(2: School of Cyberspace Security, Huazhong University of Science and Technology, Wuhan 430074, P. R. China)
(3: Wuhan Sixiang Technology Co., LTD., Wuhan 430074, P. R. China)
降雨概率分布是水文、气象、工程设计等众多部门一直关心的问题,在定量降雨估算、天气气候数值模式、洪水预报等科研中被广泛应用。有百年历史的极值理论(extreme value theory,EVT)对其计算产生深远影响,自1941年耿贝尔成功将EVT应用于洪水频率分析后至今仍在沿用。当前的研究侧重于极值降雨概率分布(probability distribution of extreme value precipitation,PDoEVP)、极端降雨概率分布(probability distribution of extreme precipitation,PDoEP)。PDoEVP采用块(例如年)最大值法[1-7],PDoEP采用非最大值法,包括多个样、超阈值、超分位数值等多种取样方法[4, 6, 8-15]。由于样本有限性、资料代表性、降雨的地域性差异、极端降雨样本的稀缺性、观测网对罕见降雨的捕获能力等,众多研究结果大相径庭,学派间各执一词,虽然经历了大半个世纪的研究,理论分布函数尚无国际公认的统一模型,多名学者“曾对城市设计暴雨频率分布线型的问题发表过不同意见,展开学术争鸣与讨论”[15];暴雨强度公式在我国多种技术规范或设计标准中是工程设计的依据,我国推荐了PDoEVP方法,计算模型推荐了指数、皮尔逊Ⅲ分布,也有的推荐了皮尔逊Ⅲ、耿贝尔分布,而美国推荐[11]耿贝尔、对数正态分布。由于暴雨强度公式主要用于解决工程设计问题,关注重点在2~20年重现期范围,其技术粗糙性得到谅解,分歧被搁置,导致应用研究与需求脱节, 标准或规范制定中严肃性、科学性大打折扣,严重限制了相关地方标准或规范的研制进度。
PDoEVP、PDoEP方法仅采用极少部分样本,能减少大量工作量,但禁锢了学界的研究思路。如迪米崔斯(Demetris)[16]认识到:年最大值和超阈值抽样法会遗漏降雨序列中隐含的有用信息,而降雨全序列保留了完整的降雨信息,能解决前者带来“设计暴雨强度”偏差的问题;也有学者挣脱EVT的束缚,以求真态度弃简就繁,直接针对降雨序列,而非极值或极端降雨序列开展研究,顾学志等[17]利用我国日降雨资料对7种函数进行拟合试验与拟合优度评价。还有学者针对逐时降雨开展了研究:王磊等[18]对祁连山中段葫芦沟流域湿季小时降雨分析了测站高度对降雨结构的影响;赵琳娜等[19]用33年夏季小时降雨资料以及台风路径观测数据分离出台风降雨后拟合降雨概率密度函数参数,得到台风小时降雨总的概率分布特征;王彬雁等[20]用皮尔逊Ⅲ型函数对四川省测站降雨进行概率密度拟合,根据降雨累积概率空间分布的拟合函数,计算了最大逐时降雨量的概率密度及其重现期。这些研究采用了伽玛分布或其变形,使用了极大似然估计法(maximum likelihood estimation,MLE)。沈铁元等[21]在我国暴雨洪涝灾害易发区选择了6个分区进行逐时降雨类条件概率密度的分区比较,并通过大量拟合试验从十多种拟合函数中挑选出了形式简单、普适性好的函数提高了拟合精度,得到了高精度的3类类条件概率密度(class conditional probability density,CCPD)算法。但仍需要对众多函数的适用性问题从理论上进行梳理与分析。类条件概率密度是指在某类别状态或定条件下的概率密度,CCPD1指有观测降雨条件下逐时降雨量的概率密度,CCPD2指逐时降雨观测有连续性降雨条件下过程降雨量的概率密度,CCPD3指逐时降雨观测有连续性降雨条件下降雨小时数(过程历时)的概率密度。
在全球变暖、极端降雨多发的背景下,在观测资料的时空密度大幅提高与年限继续增加的情况下,有必要采用降雨大样本直接从概率密度的角度开展研究,以新的资料与数学方法开展降雨概率密度函数(probability density function, PDF)研究,并发展极端降雨概率分布的理论框架,将能解决重现期计算的科学性问题,提高暴雨强度公式的科学水平。其中关键点在于通过函数的适用性分析,发现普适性强的理论密度函数。为此对20种常用概率分布从理论上对降雨概率密度的适用性进行推导与分析,筛选出适用函数后,进行拟合试验,通过拟合效果分析优选理论分布函数。
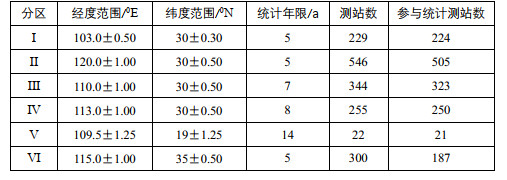
1 资料情况简介30°N线上我国东部的地区受季风影响,湿润多雨,属于我国暴雨洪涝灾害易发区,与30°N线上其它地区炎热干燥少雨的气候形成鲜明对比。为了解这里降雨特征,在30°N线上我国第二、三阶梯地形内各选2个分区,Ⅰ、Ⅲ分区位于第二阶梯地形左右两侧,Ⅳ、Ⅱ分区位于第三阶梯地形左右两侧,同时为了对比,在其南、北各选择了一个分区,分区编号按降雨频率排序。附表Ⅰ为6个分区的经纬度范围与资料年限、测站数,四川雅安在Ⅰ分区,Ⅱ分区位于杭州湾以西,离海洋近,受海洋性气候影响最盛;Ⅲ分区可代表鄂西南,Ⅳ分区可代表江汉平原南部,两分区距离较近有利于比较阶梯地形二、三阶过渡处的降雨特征;第Ⅴ分区为海南全岛,代表了海洋性气候对降雨的影响;第Ⅵ分区在郑州附近,可代表季风影响明显开始减弱的区域。
资料时间段为2015-10-29至2020-10-28。资料类别包括逐时降雨资料、质控码、观测时间。对质控码为0、3、4的数据是通过了质量控制的资料,予以采用,对质控码为7、9的数据进行极值检验、一致性检验后选择性采用或作为缺测处理(7代表“无观测任务”,9代表“未进行质量控制”),其余质控码的数据一律以缺测处理。剔除缺测率高于4 % 的测站。6个分区内国家气象站和区域雨量站近1700个,参与统计的有效站数参见附表Ⅰ,其中第Ⅴ分区的21个站全部是国家站。
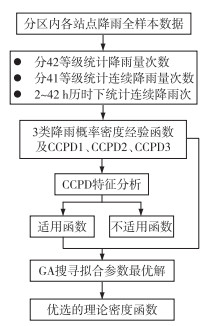
2 研究思路与方法本文研究方法与传统极值理论的方法在研究对象、采样方法、拟合方法等方面不同,图 1给出了本文优选理论密度函数的技术流程,具体步骤为:根据分区内各站点降雨全样本数据,将降雨量划分42个分箱(bins)或等级,降雨历时从2~43小时也分成42个分箱,分区内多站并和统计降雨量、连续降雨量位于各分箱内的次数,以及不同降雨历时下连续降雨次数,得到三类降雨概率密度经验函数以及三类CCPD,再分析归纳CCPD函数的特征,作为筛选适用函数的条件,对众多分布函数进行筛选,过滤掉不适用函数,然后用基因遗传算法搜寻适用函数的拟合参数最优解,并计算误差、决定系数等拟合统计量,比较分析统计量好中选优,最后给出理论密度函数。
|
图 1 优选理论密度函数的技术流程 Fig.1 Optimization flowchart of theoretical density function |
在讨论概率分布问题时包括两种数学表述:概率密度函数(PDF)、累积概率分布函数(简称概率分布函数,CDF)。CDF曲线尾部的值无限趋于1,而PDF值对降雨而言尾部值无限趋于0,在使用CDF计算PDF时是由大量小差而得,且有多个量级差别,会导致函数曲线尾部的相对拟合偏差大,在拟合降雨概率分布时采用CDF是一种粗糙的技术处理方式,意在提高拟合精度,尤其是当关注点在曲线尾部的罕见降雨事件时,就要使用PDF拟合而非CDF。为此针对逐时降雨PDF开展研究,又由于PDF在[0.1, ∞)内数学上与CCPD1存在倍率关系,故本文将研究对象由PDF转变为CCPD1,另外增加了对CCPD2、CCPD3的研究,是针对连续性降雨过程,在雨量、历时上的概率分布。3类CCPD的自变量x1、x2、x3分别对应为逐时降雨量、逐时连续降雨(HCR)过程降雨量、HCR历时(HoCR,记为HoCR)。CCPD1定义域为x1 =Rain≥0.1 mm,对CCPD2为x2=Rain2≥0.2 mm,对CCPD3为x3 =HoCR≥2 h。本文以这三类CCPD为研究对象,开展了函数适用性分析、拟合试验以及优选理论密度函数。
PDoEVP、PDoEP采用了降雨事件的少量样本,对降雨概率密度是一种有偏估计,适用雨量范围与地域均有限。有别于它们,本文在样本选择上采用了降雨事件的大样本,即一个分区内多站降雨序列的全样本。相较PDoEVP而言这种样本选择方式是回归降雨概率事件本位,能更客观地描绘降雨事件概率分布全貌,属无偏估计,有关样本数量不足、经验函数失真、经验函数的光滑性不够等具体技术问题能得到解决,这是提高拟合精度的基础,有利于发现恰当的理论密度函数。
2.2 函数适用性分析、理论密度函数选取根据6个分区3类CCPD函数图像,可分析出在由原坐标、对数坐标所组合出的4种坐标系下函数的单调性、凹凸性,另外参比指数函数、幂函数分析CCPD尾分布特性。本文中对数均指自然对数。
把CCPD这些特性作为参比函数的筛选条件,对20种常用函数逐一筛选,如某一条件不符,则认定对CCPD不适用,意味对PDF也不适合;符合条件的定为适用函数,对它们开展拟合试验,分析比较加性、乘性2种误差模型下的拟合误差。根据拟合误差,结合贝叶斯信息准则(Bayesian information criterions,BIC)、函数性质等来判断哪种适用函数更恰当,最终确定理论密度函数。
2.3 拟合方法在求解概率分布参数方面方法很多,经典的是MLE、矩估计法(method of moment estimation,MoME),1995年Singh和Guo[22]提出最大熵法(principle of maximum entropy,PoME),2013年Krylov等[23]提出的对数累积量(method of Logarithmic cumulant,MoLC)参数估计方法,Li等[24]认为MoLC也有局限性;另外部分学者采用了参数分离法,如秦先祥等[25]、Song[26]、张珊珊等[27]采用基于SISE(scale-independent shape estimation)方程的方法。多数方法需要求解联立方程组,会出现方程组无解、多解的困难[28],形式上是在求取精确解,实质依然是近似解;再者这些文献中多针对不同的单一函数,不便于函数的优选;还有,许多分布函数参数不能满足独立性条件,这些方法不适用。为此,采用基因遗传算法(genetic algorithm,GA),能减少方程推导、简化计算步骤,还能增强方法的普适性、提高拟合精度。本文选择GA通过设定综合考虑了乘性与加性误差模型的目标函数,来搜索多目标参数的最优解,以此兼顾曲线头尾、提高整体拟合精度。
用PM表示某一分区(M)某一类CCPD的经验函数,用YM表示其拟合函数。
对3类CCPD目标函数均设为:
| Obj=E0(PM)+EL(PM)={ERMS(PM−YM)Max(PM)+ERMS[ln(YM/PM)]ln[Max(PM)Min(PM)]}100 | (1) |
式中,ERMS为均方根误差算子,E0(PM)、EL(PM)分别为对PM、ln(PM)归一化后的均方根拟合误差,E0、EL分别与加性、乘性误差模型下的相对拟合误差大小紧密相关。E0主要误差贡献由曲线头部决定,中部贡献小、尾部贡献近乎0;EL与所有数据点上的相对误差相关,曲线尾部贡献比头部大。如此设定目标函数能兼顾到各个数据点上的相对误差,对曲线尾部CCPD趋于0的数据点,能有效提高拟合精度,从而兼顾到拟合曲线的首尾。
3 逐时降雨CCPD经验函数的特性以下通过分析给出了CCPD的7项特性,是开展函数适用性分析的基础,也是筛选函数的条件。
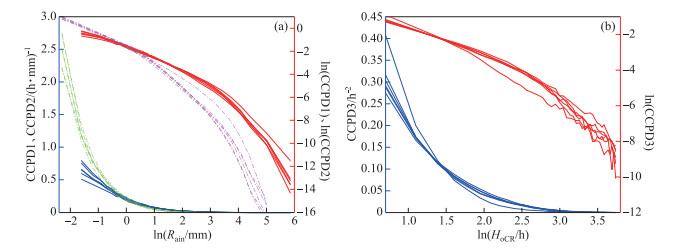
图 2给出了6个分区3类CCPD的经验函数分布,采用了一线两画方式:纵坐标有左右之分,一张图上同时绘制y、ln y的曲线分布,以蓝色标示的左轴为y,以红色标示的右轴代表ln y。函数横、纵坐标为对数坐标时分别记xL=ln x、yL=ln y,4种坐标搭配下一阶导数分别记为:
|
图 2 CCPD1(绿)、CCPD2(蓝)、lnCCPD1(粉红)、lnCCPD2(红)(a);CCPD3(蓝色,对应左边蓝色y轴)、lnCCPD3(b) Fig.2 CCPD1(green), CCPD2(blue), lnCCPD1(pink), lnCCPD2(red) (a); CCPD3(blue), lnCCPD3(red)(b) |
根据图 2可得出CCPD的1st.至4th.特征,是函数在4种坐标系下的单调性、凹凸性:1st.(x, y)坐标下,3类CCPD满足y′ < 0,y″>0,即函数曲线单调凸减;2nd.(xL, y)坐标下,三类CCPD满足y′Lx < 0,y″Lx>0,即函数曲线随xL单调凸减;3rd.(x, yL)坐标下,三类CCPD满足y′Ly < 0,y″Ly>0,即函数曲线随x单调凸减;4th.(xL, yL)坐标,即双对数坐标下,三类CCPD满足y′LL < 0,y″LL < 0,即函数曲线随xL单调凹减。
根据图 3并结合了具体数据表得出5th.特性以及6 th.的有界特性;7th.是重尾分布特性,紧随其后有具体说明。
|
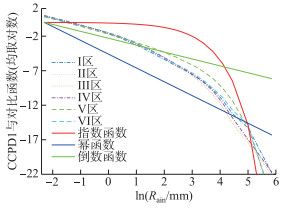
图 3 双对数坐标下CCPD1经验函数与指数函数、幂函数、倒数函数的对比 Fig.3 Comparison of the CCPD1 empirical function with exponential, power, reciprocal functions under double log coordinates |
5th.在双对数坐标下,CCPD1曲线头部y″ LL近似为0,左边界附近(0.1 mm≤Rain < 1 mm区间)曲线近似线性分布,曲线斜率y′LL有界且接近常数-1,变化范围大致为(-1.1, -0.95);曲线尾端,如Rain>100区间,曲线倾斜度较大,y′LL < -4。由此得出逐小时降雨出现频率与雨量的关系表现为:小降雨区段近似呈反比例关系;而极端降雨区段近似呈ń次幂反比关系,且4 < ń < 9,即在降雨量降低一半时概率密度增长至少翻4翻;6th. CCPD头部(x取值小)有上确界、尾部(x大时)有下确界且趋近于0,期望值、均值、方差有界;7th. CCPD属于重尾(Heavy-tialed)分布,且尾部递减率介于幂函数与指数函数之间。
重尾分布来自于1982年由Embrechts给出的第一条定义, 其应用最为广泛[29],略去数学式可简单表述为:如果某分布函数不存在指数阶矩,或不存在矩母函数, 称其属于重尾分布,否则属于轻尾分布。通俗理解为:重尾分布的尾部比指数分布要厚实,密度函数尾端递减率小(降速慢)。
图 3给出了在双对数坐标(xL, yL) 下CCPD1经验函数与指数函数、幂函数、倒数函数的对比图,指数函数、幂函数、倒数函数分别为exp(-0.1x)、100x-2、10/x,均递减,双对数图上也递减。从图中可看出:CCPD1在定义域内各处均递减, 且指数函数比CCPD1在尾部倾斜度(或递减率)大,即斜率小,表明CCPD1遵从某种重尾分布;还可看出幂函数、倒数函数呈直线分布,斜率固定,在尾端比ln(CCPD1)大、斜率大、递减率小,表明CCPD1尾端比幂函数更接近于0轴、递减率更大。CCPD的拖尾比幂函数轻、比指数函数重,且尾端密度函数遵从递减率介于幂函数与指数函数之间的重尾分布。
为此可判定指数函数、幂函数不适用于拟合CCPD。具体判据可由CCPD的特性得出:指数函数y″Ly=0不满足3rd.条,幂函数y″LL=0不满足4th.条,倒数函数不满足3rd.和4th.条。并且依靠增加和调整参数不能调和与CCPD曲线走势的结构性矛盾,难以使拟合曲线首尾兼顾。
4 常用概率分布函数对逐时降雨CCPD的适用性分析类似CDF是PDF的不定积分,CCPD的不定积分称为(累积)类条件概率分布,简记CCCD,下文数学推导过程中需用到CCPD、CCCD的数学符号,分别记为y、Y,对给定的参数集有:
| y=P(X=x)=f(x;ϕ);Y=P(X<x)=F(x;ϕ)=∫x0y dx | (2) |
指数分布属轻尾分布,其不适用性前面已进行了讨论;指数分布是轻尾与重尾分布的分界线,而CCPD是遵从重尾分布,可以推断轻尾分布的函数均不适用于CCPD,诸如:正态(Normal)、拉普拉斯(Laplace)、瑞利(Rayleigh)、纳卡加米(Nakagami)、玻尔兹曼(Boltzmann)、二项(Binomial)、几何(Geometric)分布。耿贝尔(Gumbel)分布也属轻尾分布,由于其应用广泛,以下予以说明;另外以多项式(Multinomial)分布为例给出了不适用的简要证明。
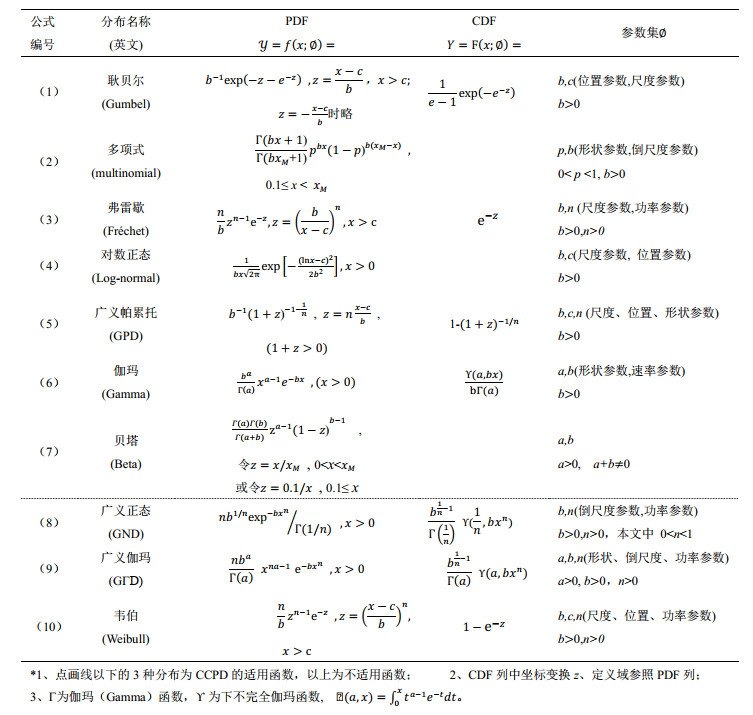
附表Ⅱ为常用降雨概率密度分布函数,主要给出了下文推导中用到的10种分布,Normal、Laplace等轻尾分布略,莱维、广义逻辑、广义柯西等重尾分布也略。
Gumbel分布是广义极值(GEV)的I型分布,在量化洪水、极端降雨相关风险方面历史悠久,是我国、美国在暴雨强度公式编制中推荐使用的理论分布函数之一,在极端降雨重现期、概率分布方面是世界流行模型,有着广泛的应用。由于Gumbel分布左、右支尾部均小于exp(-z),均属轻尾分布,且右支拖尾比左支重,故附表Ⅱ中仅列出了右支(x>c时) 两参数Gumbel分布的公式,编号(1),由其PDF式可得:y″Ly < 0, 不符合3rd.条,故不适用。将之用于拟合CCPD时会使尾端递减率高估、概率密度偏小、重现期高估、极值降雨量低估,使设计暴雨强度偏小,即放宽了设计需求、工程预算低估,便增加了致灾风险。早在2004年希腊科学家迪米崔斯[30-31]就得出了与此相同的结论,王颖等[32]对重庆市极值降雨的研究中没发现服从Gumbel分布的站点,佐证了该结论。
附表Ⅱ中公式(2)列出了Multinomial的PDF,由其可得y″Ly=0,与3rd.条中y″Ly>0矛盾,不适用。
所以适用函数需要从重尾分布中挑选,以下分别对有关重尾分布的不适用性予以证明。
4.1.2 弗雷歇分布——GEVII型分布不适用性证明GEV分布历史悠久,在极端降雨概率分布方面近期仍大量开展的模型,其包括三个分型,Ⅰ、Ⅱ、Ⅲ型分别为:Gumbel、弗雷歇(Fréchet)、韦伯(Weibull)分布。前面已分析了Gumbel,下面来分析Fréchet分布,附表Ⅱ中公式(3)列出了其CDF、PDF。
Fréchet分布在不同参数取值条件下能分别满足CCPD特征,但是不能同时满足5th.条曲线头部、尾部特征。由(3)式得:y′LL=nbnx-n-n-1,由第iv特征中双对数图上尾部递减率大于4.5可知n >3.5,以CCPD1为例,右边界处x=x0=0.1,此时y′LL|x=1-y′LL|x=0.1=bnn(0.1-n-1)≈n(10b)n, 对于曲线头部近呈似线性关系要求满足y′LL|x=1-y′LL|x=0.1 < 0.15,即有(10b)n < 0.15/n,于是b < 0.05。b < 0.05时,bnnx-n < 0.5,致y′LL >4,即双对数图上头部递减率过大,y′ LL≈-1不能成立;另外曲线尾部及中部bnnx-n≈0,y′LL≈-n-1,全域内双对数图上曲线近似呈线性关系,仅仅在头部斜率通过bnnx-n进行了微小的修正,显然与CCPD1图形不符。CCPD2同样存在类似问题,故Fréchet分布不适用于CCPD。
4.1.3 对数正态分布不适用性证明对数正态(Log_normal)分布是美国暴雨强度公式编制中推荐的理论分布函数之一,附表Ⅱ中公式(4)列出了其PDF。其满足1st.至4th.条中单调凹凸性,但是难以使曲线头、尾同时满足5th.条:由(4)式可得y′LL=-1-x-1ln ax/σ2,y″LL=x-1(ln ax-1)/σ2,当a取值在10附近时满足5th.条中曲线头部斜率y′LL约为-1,而y″LL < 0需要a < 2.71828/x,即a至少比0.01更小。这种参数取值的矛盾使得在拟合试验中以乘性误差模型统计的误差总是偏大,即双对数图上曲线头尾难以兼顾,故不适用于CCPD。
4.1.4 广义帕累托分布(GPD)不适用性证明GPD将指数分布与幂函数融为一体,是把Pareto分布中幂指数广义化以及坐标变换后而来,在多学科领域均有应用,在极端降雨重现期、概率分布方面有长期与广泛的研究。由于前述CCPD遵从拖尾递减率介于幂函数与指数函数之间的重尾分布,似乎与GPD存在共通点、有理由认为GPD对CCPD具有适用性,但其实不然,简要推证参见附件一。
4.1.5 伽玛分布、皮尔逊Ⅲ型分布不适用性证明伽玛分布被降雨发生器、气候模式等中普遍采用,在极端降雨概率分布的研究方面也较多,但是对于逐时降雨CCPD不适用,证明过程见附件二。
皮尔逊Ⅲ型分布是在伽玛分布基础上增加了位置参数,进行坐标变换后函数,拟合试验中相对伽玛分布拟合效果有所改善,但程度非常有限,仍然难以首尾兼顾,所以也不适用。
4.1.6 贝塔、莱维、广义逻辑、广义柯西分布不适用性证明或分析贝塔函数对于CCPD的不适用性证明见附件三。
莱维(Lévy)分布不满足递减条件,且尾部渐进等价于(用符号~表示)指数为-3/2的幂律分布,即双对数图上曲线尾部斜率为-1.5,与5th.条不符,其一、二阶矩不存在,与6th.条不符,故不适用;广义逻辑(Logistic)分布在函数尾部渐进等价于(~)指数函数,判断对CCPD不适用;柯西(Cauchy)分布也称为洛伦兹(Lorentz)分布,其累积分布函数为反正切(arctan)函数。广义Cauchy分布是将Cauchy密度函数中的幂次数参数化而来,以幂函数为主体结构,具有厚重的拖尾概率,期望值无界,据4th.条判断其对CCPD不适用;对数柯西分布比柯西分布拖尾更厚重,对CCPD不适用。
4.2 筛选结果——适用函数广义正态分布(GND)、三参韦伯分布符合CCPD各函数特性,通过了筛选,两者均是广义伽马分布(GΓD)的特例,为此本文选中的三种适用函数为GND、GΓD、Weibull分布,PDF见附表Ⅱ尾部。
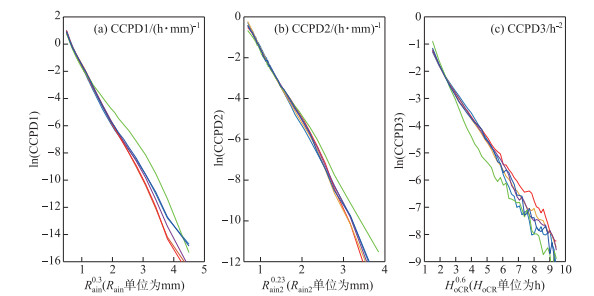
4.2.1 广义正态分布的适用性分析图 4给出了各分区3类CCPD取自然对数后与xn的线性关系,其中a、b图的x对应降雨量,c图的x对应连续降雨历时HoCR。不难看出均呈现出良好的线性关系,而且图中是以幂指数n分别取0.3、0.23、0.6三个定值为例给出的,适当调整n的取值将能获得更优的线性关系。为此可以用一种指数为幂函数的指数函数ea-bxn来拟合3类CCPD,有称其为Exponential power distribution[33],也有简称为指数幂分布[34],更贴切的简称可为幂律指函数,但仍易被误解,不建议用此类简称。文献[21]通过大量拟合试验验证了用其拟合CCPD可达到很高的拟合精度,但是其不能严格满足定义域内积分为1,增加这一约束条件下,参数减少,函数也变成了GND。
|
图 4 各分区CCPD1、CCPD2、CCPD3取对数后与xn的线性关系 Fig.4 Linear relationship between logarithms of CCPD and xn in six subregions |
GND由Subbotin(1923)将正态分布中的幂指数2进行泛化而来。其PDF具有函数形式简洁的优点,在n < 1时GND函数凸减、左边界处函数有界。对于降雨的CCPD,n取值范围将缩小到(0.1,1)区间,拟合试验中n的主要取值范围对于3类CCPD分别在0.24~0.35、0.2~0.25、0.5~0.7很小的区间变化,这为参数寻优带来便利。
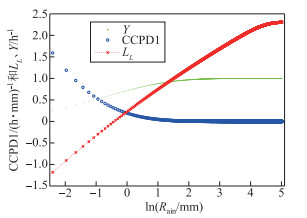
4.2.2 三参韦伯分布的适用性分析GEVⅢ型是x取倒数后x负半轴的Fréchet分布。为适用CCPD仍选x正半轴来处理,对(3)式进行坐标变换,自变量转换为x的倒数,便由Fréchet分布变成韦伯分布,在n < 1条件下CCPD 7项特征能同时符合。增加了位置参数c后三参韦伯密度函数由附表Ⅱ中(10)式给出,根据其不定积分(即累积概率分布,记为Y),记Y=1-Y可得:ln(-ln Y)=a·ln(x-c)-a·ln b,与ln(x-c)呈线性关系。为此根据第Ⅵ分区CCPD1计算ln (-ln Y),记为LL,图 5给出了第Ⅵ分区CCPD1、Y、LL随ln Rain的分布情况,图中LL曲线近似呈线性,反映出三参韦伯分布对CCPD具有适用性。其它分区曲线走势雷同,故略。
|
图 5 第Ⅵ分区CCPD1、Y、LL随lnRain的分布 Fig.5 The distribution of CCPD1 and LL, Y with lnRain in the Ⅵ subregion |
GΓD是一个庞大的概率分布家族,整合了多种分布函数,具有灵活的统计特性。GND、韦伯分布是GΓD的特例,GΓD也应适用。
GΓD在na≥1时右边界x=0处有界,否则无界;GΓD在n≥1属轻尾分布,否则属重尾分布。该函数中参数n、a、b不满足独立性条件,取对数后亦然,不宜采用MLE、POME、参数分离等参数估计方法。
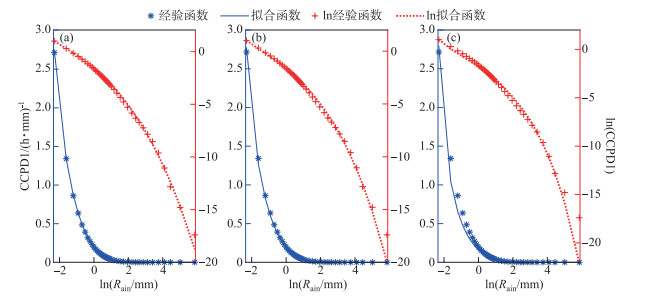
5 拟合试验结果分析 5.1 CCPD1的拟合结果第Ⅴ分区是拟合效果最差的分区,拟合误差最大、决定系数(或称拟合优度)最小,图 6便以Ⅴ分区为例,采用一线两画方式,给出了3种拟合函数(对应a、b、c图)第一类类条件概率密度CCPD1经验函数(*、+离散点)与拟合函数(线、虚线),蓝色(点和线)对应左边y轴,红色对应右边y轴(对数坐标)。由于其它分区的图与Ⅴ分区雷同,故图略,并且各分区间CCPD1差别小、相似性好,曲线重合度高,不便在图中同时给出。从中看出:GΓD(图 6a)、GND(图 6b)蓝色线与蓝色*离散点、红色线与红色+离散点吻合度高,即两函数对CCPD1有很强的拟合能力;三参韦伯函数(图 6c)有较强的拟合能力,但蓝色线与蓝色*点在曲线头部(弱降雨区段)出现误差,拟合效果较前两者相对差。
|
图 6 第Ⅴ分区CCPD1经验函数与拟合函数(图a、b、c分别对应GΓD、GND、三参Weibull分布) Fig.6 CCPD1 empirical function of the Ⅴ subregion and fitting function (Fig.a, b, c correspond to GΓD, GND and Weibull) |
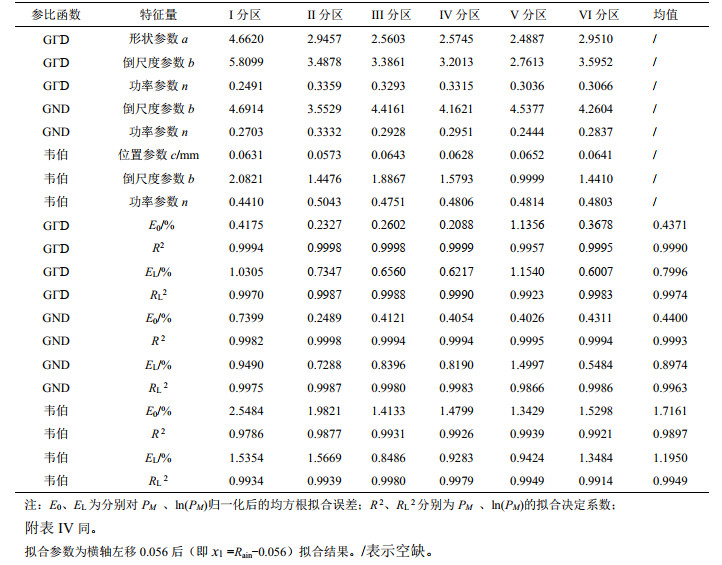
附表Ⅲ分别给出3种拟合函数对6个分区CCPD1的拟合参数与拟合统计值,拟合时对x轴进行了左移0.056 mm的处理,拟合参数供参考与验证。从三参韦伯函数6个分区相对拟合误差来看,对于CCPD1均小于2.55 %,对ln(CCPD1)均小于1.67 %;6个分区的决定系数,对CCPD1均大于0.97,对ln(CCPD1)均大于0.99,可以说三参韦伯函数对CCPD1有较强的拟合能力,但通过其与其它函数的比较知道,GΓD、GND函数比其更强。
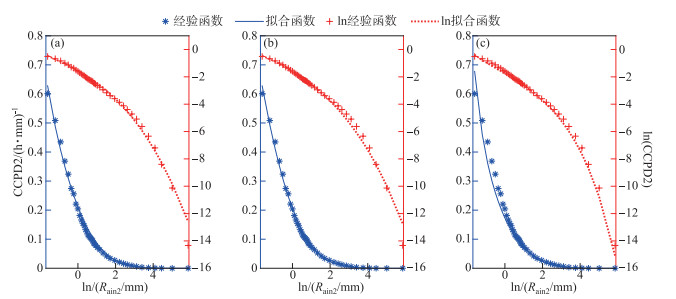
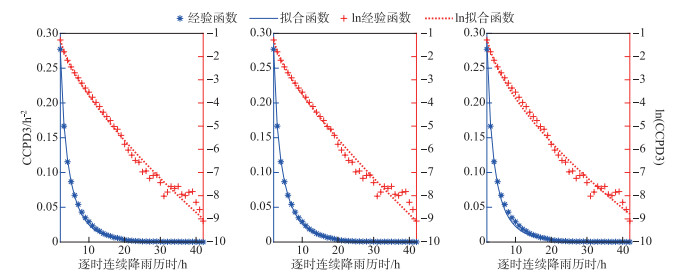
5.2 CCPD2、CCPD3的拟合结果第Ⅱ分区拟合CCPD2的效果6个分区中最差,图 7便以Ⅱ分区为例给出了CCPD2经验函数与3种拟合函数;第Ⅰ分区拟合CCPD3的效果6个分区中最差,图 8以Ⅰ分区为例给出了CCPD3经验函数及3种拟合函数。从两图中分析的结论与图 6相似:3种概率分布均能很好地拟合CCPD2和CCPD3,仔细比较图c中蓝实线与*离散点能看出三参韦伯分布的拟合效果相对其它2种函数要差。
|
图 7 第Ⅱ分区的CCPD2经验函数与拟合函数 Fig.7 CCPD2 empirical function of the Ⅱ subregion and its fitting function |
|
图 8 第Ⅰ分区第三类类条件概率密度CCPD3经验函数及其拟合函数 Fig.8 CCPD3 empirical function of the Ⅰ subregion and its fitting function |
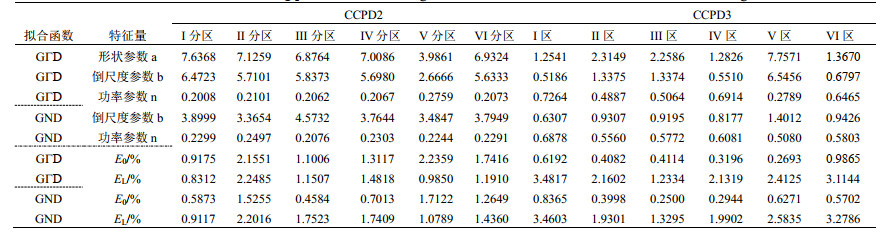
附表Ⅳ给出对6个分区CCPD2、CCPD3的拟合参数与相对拟合误差,由于三参韦伯分布拟合效果要低于GΓD、GND,两表中均省略了三参韦伯分布的数据,同时由于决定系数均大于0.98且基本大于0.99,仅CCPD2有2个、CCPD3有5个数据小于0.99,故表中也略去了决定系数。前面附表Ⅲ中反映的是GΓD比GND有微弱的优势,而4中不然,GΓD与GND平均误差数据非常接近,两者互有优势:对CCPD2,GΓD比GND的E0大、而EL小,对CCPD3,EL有半数分区小,而另外半数分区大,E0亦然, 难以判断两者优劣。在GΓD具有广谱性且比GND多出1个参数的情况下,GND与GΓD拟合精度相当。
6 优选理论密度函数从上面分析知道GΓD、GND对三类CCPD的拟合均能达到很高的精度,拟合误差将受到观测误差、统计误差的干扰、混淆,当拟合误差与观测、统计误差相当时,比较拟合误差及有关拟合统计量已经失去意义,综合以下3点来判断,GND是最优选择:
① 由于GND仅含两个参数,比三参GΓD少,根据BIC[35],在拟合精度相当时,BIC与参数的多少呈正比,参数少的模型成为优选者;
② GΓD比GND具有广谱性,广谱性是“双刃剑”,模型复杂度增大,容易造成过拟合现象,在经验函数包含误差及经验函数的离散点数量偏多时将体现出广谱性的弱点;
③ GND是GΓD的特例,GND函数有界、递减,而对于GΓD函数,递减与有界(x=0处)两者互为矛盾,即na<1时GΓD函数递减但无界,na>1时有界但非递减。
既然二参GND拟合时已具有高精度、强普适性,首推为理论密度函数。采用降雨PDF方法替代传统的年极值法,使重现期计算更准确有效,能提高暴雨强度公式的科学性,拟合的高精度与函数的普适性有望解决降雨概率分布模型统一的问题。
7 结论与讨论1) 根据逐时降雨的3类“类条件概率密度函数”增减、凸凹等特性,理论上对20种函数进行了适用性分析,筛选出3个适用函数:GΓD、GND、三参韦伯函数,三者对所选分区3类CCPD均具有较强的拟合能力,其中GΓD、GND拟合效果更好。
2) GΓD拟合3类CCPD时误差最小;GND是GΓD的特例,在少1个参数情况下能和GΓD拟合精度相当,首推为理论密度函数。
3) 选择基因遗传算法直接多参数寻优得到近似解,可避免常用求解概率分布参数方法中推导复杂、计算步骤多的不足,且综合考虑乘性误差与加性误差而设置的目标函数可以使拟合曲线头尾兼顾。
4) 极值降雨概率分布由于仅采用极少部分降雨样本,虽然能减少工作量,但禁锢学界的研究思路。采用降雨PDF方法替代传统的年极值法,使重现期计算更准确有效,能提高暴雨强度公式的科学性,拟合的高精度与函数的普适性有望解决降雨概率分布模型统一的问题。
5) 采用耿贝尔、指数等轻尾分布拟合降雨概率密度时会使函数尾端递减率高估、概率密度偏小、重现期高估、极值降雨量低估,使设计暴雨强度偏小,即会放宽设计需求、低估工程预算,从而增加致灾风险。
讨论:本文仅对6个分区的逐时降雨进行了拟合试验,更多地域、更多时间尺度的降雨特征需要统计与分析,从而使结论得到更广泛的检验,解决模型统一的问题仍需大量研究。根据CCPD1、CCPD2的拟合结果可估算年均降雨量AAR、连续降雨的年均贡献,AAR估算精度的分析也可反过来分析函数的选取是否恰当。根据高精度的降雨概率密度拟合结果,才可以估算罕见降雨事件的特征值,如可能最大降雨量PMP、极端降雨重现期、重现期降雨量、分位数降雨量等,否则由于偏差过大而失去意义。
8 附录附件1~3和附表Ⅰ~Ⅳ见电子版(DOI: 10.18307/2023.0230)。
附录附件一:广义帕累托分布(GPD)不适用性证明
附表Ⅱ中公式(5)为GPD的PDF、CDF,当位置参数c距x的左边界较远时会明显缩小x的取值范围,即对概率事件设定阈值挑选样本,所以也被称为阈值参数。当n>0时,b>0;当n<0时,- 1<z<0。当n=0时转化为指数函数,对CCPD不适用,所以取n≠0。
由于CCPD、CCCD均非负,y、Y、1 − Y > 0,所以取b> 0;
当n<-1时,密度函数递增,所以取n>-1;
由(5)式得:
由3rd.条件yLy″ < 0, yLy″ > 0得(1+1/n)>0,所以n取值范围缩小为n >0;
再有:
附件二:广义帕累托分布(GPD)不适用性证明
附表Ⅱ中(6)式为两参伽玛密度函数,对降雨而言取x >0,可得:
①在a=1时褪变为指数函数,对CCPD不适用;
②在a<1时满足凸减条件,但属轻尾分布,对CCPD尾部不适用;
③在a>1时为重尾分布,但不满足2nd.与3rd.中凸减条件,及4th.中递减条件,对CCPD不适用;这导致了拟合试验中用伽玛分布难以首尾兼顾,对CCPD不适用。
附件三:贝塔不适用性证明或分析
附表Ⅱ中(7)式为贝塔(Beta)密度函数,下面根据两种坐标转换的方式分别处理:
其一是令z = x/xM, 取Max(x)为最大可能逐时降雨量xM,或者人为设定某降雨量大值。由1st.条中y′ < 0得a < 1, b > 1;由上式可得:
其二是令z = 1/x,不需要设定xM,与上类同,也不适用于CCPD。
| 附表Ⅰ 6个分区经纬度范围与资料年限、测站数 Appendix Ⅰ Latitude and longitude range, data age, number of stations of six subregions |
| 附表Ⅱ 降雨概率密度常用分布函数 Appendix Ⅱ Commonly used distribution function of rainfall probability density |
| 附表Ⅲ 各分区CCPD1拟合参数与拟合统计量 Appendix Ⅲ Fitting parameters and statistical values of CCPD1 in six subregions |
| 附表Ⅳ 各分区CCPD2、CCPD3拟合参数与相对拟合误差 Appendix Ⅳ Fitting parameters and fitting relative deviation of CCPD2 and CCPD3 in six subregions |
| [1] |
Mao HQ, Du YD, Song LL. Research on probability distribution models of short-period precipitation extreme in Guangzhou. Meteorological, 2004, 30(10): 3-6. [毛慧琴, 杜尧东, 宋丽莉. 广州短历时降水极值概率分布模型研究. 气象, 2004, 30(10): 3-6.] |
| [2] |
Yao L, Zhao SR, Zhao CG et al. Temporal and spatial distributions of hourly rain intensity and recurrence periods in Eastern and Central China. Acta Geographica Sinica, 2010, 65(3): 293-300. [姚莉, 赵声蓉, 赵翠光等. 我国中东部逐时雨强时空分布及重现期的估算. 地理学报, 2010, 65(3): 293-300.] |
| [3] |
Zhang LP, Yang YR, Qin LL et al. Distribution of extreme precipitation events in water source area for the middle route project of south-to-north water transfer under A2, A1B, B1 scenarios. Progressus Inquisitiones de Mutatione Climatis, 2013, 9(1): 29-34. [张利平, 杨艳蓉, 秦琳琳等. 未来情景下南水北调中线工程水源区极端降水分布特征. 气候变化研究进展, 2013, 9(1): 29-34. DOI:10.3969/j.issn.1673-1719.2013.01.005] |
| [4] |
Zhang YH, Wang CX, Liu KL et al. Applicability of different probability distributions to estimated extreme rainfall. Scientia Geographica Sinica, 2015, 35(11): 1460-1467. [张玉虎, 王琛茜, 刘凯利等. 不同概率分布函数降雨极值的适用性分析. 地理科学, 2015, 35(11): 1460-1467.] |
| [5] |
Peng T, Wang JC, Shen TY. Change characteristics of extreme precipitations and estimation of precipitation in different return periods in the Qingjiang Basin of the Yangtse River. Journal of Coastal Research, 2019, 93(sp1): 200. DOI:10.2112/SI93-028.1 |
| [6] |
Wang XY, Jiang WG, Deng Y et al. Characteristic analysis and fatalness of disaster-inducing factors assessment of hourly extreme rainfall in different return periods of Beijing-Tianjin-Hebei region. Geographical Research, 2020, 39(11): 2581-2592. [王晓雅, 蒋卫国, 邓越等. 基于多重现期的京津冀小时极端降雨特征分析及致灾因子危险性评估. 地理研究, 2020, 39(11): 2581-2592. DOI:10.11821/dlyj020190781] |
| [7] |
Wang Y, Liu XR, Cheng BY et al. Probability distribution model optimization and application of multiple duration extreme precipitation in Chongqing. Journal of the Meteorological Sciences, 2020, 40(4): 560-568. [王颖, 刘晓冉, 程炳岩等. 重庆多历时极值降水的概率型优选及应用. 气象科学, 2020, 40(4): 560-568.] |
| [8] |
Hu HR, Mao XL, Liang L. Temporal and spatial variations of extreme precipitation events of flood season over Sichuan Basin in last 50 years. Acta Geographica Sinica, 2009, 64(3): 278-288. [胡豪然, 毛晓亮, 梁玲. 近50年四川盆地汛期极端降水事件的时空演变. 地理学报, 2009, 64(3): 278-288. DOI:10.3321/j.issn:0375-5444.2009.03.003] |
| [9] |
Su BD, Jiang T. Distribution feature of time series of extreme precipitation over the Yangtze River Basin. J Lake Sci, 2008, 20(1): 123-128. [苏布达, 姜彤. 长江流域降水极值时间序列的分布特征. 湖泊科学, 2008, 20(1): 123-128. DOI:10.18307/2008.0119] |
| [10] |
Si B, Yu JH, Ding YG. Research on extreme value distribution of short-duration heavy precipitation in the Sichuan Basin. Journal of the Meteorological Sciences, 2012, 32(4): 403-410. [司波, 余锦华, 丁裕国. 四川盆地短历时强降水极值分布的研究. 气象科学, 2012, 32(4): 403-410. DOI:10.3969/2012jms.0086] |
| [11] |
Tian FY, Zheng YG, Mao DY et al. Study on probability distribution of warm season hourly rainfall with Γ distribution. Meteorological Monthly, 2014, 40(7): 787-795. [田付友, 郑永光, 毛冬艳等. 基于Γ函数的暖季小时降水概率分布. 气象, 2014, 40(7): 787-795.] |
| [12] |
Cao Y, You QL, Ma QR et al. Probability distribution for the summer extreme precipitation in the Qinghai-Tibetan Plateau. Plateau Meteorology, 2017, 36(5): 1176-1187. [曹瑜, 游庆龙, 马茜蓉等. 青藏高原夏季极端降水概率分布特征. 高原气象, 2017, 36(5): 1176-1187.] |
| [13] |
Song XM, Zhang JY, Kong FZ. Probability distribution of extreme precipitation in Beijing based on extreme value theory. Scientia Sinica: Technologica, 2018, 48(6): 639-650. [宋晓猛, 张建云, 孔凡哲. 基于极值理论的北京市极端降水概率分布研究. 中国科学: 技术科学, 2018, 48(6): 639-650.] |
| [14] |
Liu J, Zhou H, Lu CH et al. A review on recent advances of urban rainfall intensity-duration-frequency relationships. Advances in Water Science, 2018, 29(6): 898-910. [刘俊, 周宏, 鲁春辉等. 城市暴雨强度公式研究进展与述评. 水科学进展, 2018, 29(6): 898-910.] |
| [15] |
Mei C, Liu JH, Wang H et al. Review on urban design rainstorm. Chinese Science Bulletin, 2017, 62(33): 3873-3884. [梅超, 刘家宏, 王浩等. 城市设计暴雨研究综述. 科学通报, 2017, 62(33): 3873-3884. DOI:10.1360/N972016-01295] |
| [16] |
Koutsoyiannis D ed. Stochastics of hydroclimatic extremes—A cool look at risk. Kallipos-Open Academic Editions, 2021.
|
| [17] |
Gu XZ, Ye L, Zhao TTG et al. Probability distribution of daily precipitation in China. Journal of Hydraulic Engineering, 2021, 52(10): 1248-1262. [顾学志, 叶磊, 赵铜铁钢等. 中国日降水量的概率分布. 水利学报, 2021, 52(10): 1248-1262.] |
| [18] |
Wang L, Chen RS, Song YX. Study of statistical characteristics of wet season hourly rainfall at Hulu watershed with Γ function in Qilian mountains. Advances in Earth Science, 2016, 31(8): 840-848. [王磊, 陈仁升, 宋耀选. 基于Γ函数的祁连山葫芦沟流域湿季小时降水统计特征. 地球科学进展, 2016, 31(8): 840-848.] |
| [19] |
Zhao LN, Bai XM, Xing C et al. Probability distribution of hourly precipitation in typhoons during summer seasons in the southeast China. Torrential Rain and Disasters, 2017, 36(2): 97-107. [赵琳娜, 白雪梅, 邢程等. 中国东南地区夏季台风小时降水概率分布特征. 暴雨灾害, 2017, 36(2): 97-107.] |
| [20] |
Wang BY, Zhao LN, Xu H et al. Probability distribution and partition of hourly rainfall during the rainy season over Sichuan Province. Torrential Rain and Disasters, 2018, 37(2): 115-123. [王彬雁, 赵琳娜, 许晖等. 四川雨季小时降水的概率分布特征及其降水分区. 暴雨灾害, 2018, 37(2): 115-123.] |
| [21] |
Shen TY, Liu J, Xiang YH et al. Partition comparison and fitting function of class conditional probability density of hourly rainfall. Torrential Rain and Disasters, 2021, 40(6): 664-674. [沈铁元, 刘静, 向怡衡等. 逐时降雨的类条件概率密度分区比较与拟合函数初探. 暴雨灾害, 2021, 40(6): 664-674.] |
| [22] |
Singh VP, Guo H. Parameter estimation for 3-parameter generalized Pareto distribution by the principle of maximum entropy (POME). Hydrological Sciences Journal, 1995, 40(2): 165-181. DOI:10.1080/02626669509491402 |
| [23] |
Krylov VA, Moser G. On the method of logarithmic cumulants for parametric probability density function estimation. IEEE Transactions on Image Processing, 2013, 22(10): 3791-3806. DOI:10.1109/TIP.2013.2262285 |
| [24] |
Li HC, Liu CA. Multitexture model of multilook polarimetric SAR data based on generalized gamma distribution. In: IEEE International Geoscience & Remote Sensing Symposium. Beijing, China, IEEE, 2016: 174-177. DOI: 10.1109/IGARSS.2016.7729036.
|
| [25] |
Qin XX, Gao G, Zhou SL et al. Method on parameters estimation of generalized gamma distribution based on SISE (scale-independent-shape-estimation) equation. Journal of Electronics and Information Technology, 2012, 34(8): 1860-1865. [秦先祥, 高贵, 周石琳等. 基于SISE方程的广义伽玛分布参数估计方法. 电子与信息学报, 2012, 34(8): 1860-1865. DOI:10.3724/SP.J.1146.2011.01260] |
| [26] |
Song KS. Asymptotic relative efficiency and exact variance stabilizing transformation for the generalized Gaussian distribution. IEEE Transactions on Information Theory, 2013, 59(7): 4389-4396. DOI:10.1109/TIT.2013.2249182 |
| [27] |
Zhang SS, Dong YY, Qiao YX et al. A novel target detection algorithm with generalized gamma distribution in SAR images. Journal of Naval Aeronautical and Astronautical University, 2020, 35(2): 167-175. [张珊珊, 董云云, 乔玉新等. 一种新的广义伽玛分布下的SAR图像目标检测算法. 海军航空工程学院学报, 2020, 35(2): 167-175. DOI:10.7682/j.issn.1673-1522.2020.02.002] |
| [28] |
Huang H, Song YP, Zhao L. Maximum likelihood estimation for numerical solution of gamma distribution parameters. Journal of Higher Correspondence Education: Natural Sciences, 2011, 24(5): 52-54. [黄华, 宋艳萍, 赵磊. 伽玛分布参数的极大似然估计数值解法. 高等函授学报: 自然科学版, 2011, 24(5): 52-54.] |
| [29] |
Chen L, Liu WQ. Classes of heavy-tailed distribution and Venn diagrams of their relations. Applied Mathematics Journal of Chinese Universities: SerA, 2009, 24(2): 166-174. [陈琳, 刘维奇. 重尾分布族及其关系图. 高校应用数学学报: A辑, 2009, 24(2): 166-174.] |
| [30] |
Demetris K. Statistics of extremes and estimation of extreme rainfall: I. Theoretical investigation. Hydrological Sciences Journal, 2004, 49(4): 574-590. DOI:10.1623/hysj.49.4.575.54430 |
| [31] |
Demetris K. Statistics of extremes and estimation of extreme rainfall: Ⅱ. Empirical investigation of long rainfall records. Hydrological Sciences Journal, 2004, 49(4): 591-610. DOI:10.1623/hysj.49.4.591.54424 |
| [32] |
Wang Y, Liu XR, Cheng BY et al. Application of generalized extreme value distribution model to short-duration extreme precipitation in Chongqing. Meteorological Monthly, 2019, 45(6): 820-830. [王颖, 刘晓冉, 程炳岩等. 广义极值分布在重庆短历时极值降水中的应用. 气象, 2019, 45(6): 820-830.] |
| [33] |
El-Monsef MMEA, El-Awady MM. Generalized exponential power distribution with application to complete and censored data. Asian Journal of Probability and Statistics, 2021, 12(1): 34-55. DOI:10.9734/ajpas/2021/v12i130278 |
| [34] |
Guan HY, Gu BQ, Xu XL. Statistical analysis of three-parameter symmetric exponential power distribution. Statistics & Decision, 2021, 37(10): 37-41. [关红阳, 顾蓓青, 徐晓岭. 三参数对称指数幂分布的统计分析. 统计与决策, 2021, 37(10): 37-41.] |
| [35] |
Wang SH, Liu G, Qi ZH. BIC scoring Bayesian network model and its application. Computer Engineering, 2008, 34(15): 229-230, 233. [王书海, 刘刚, 綦朝晖. BIC评分贝叶斯网络模型及其应用. 计算机工程, 2008, 34(15): 229-230, 233.] |
 2023, Vol. 35
2023, Vol. 35