(2: 河海大学水文水资源学院, 南京 210098)
(3: 河海大学水安全与水科学协同创新中心, 南京 210098)
(2: College of Hydrology and Water Resources, Hohai University, Nanjing 210098, P. R. China)
(3: Cooperative Innovation Center for Water Safety and Hydro Science, Hohai University, Nanjing 210098, P. R. China)
河川径流是流域水循环的重要组成部分,是实现水资源高效利用、优化调度与科学管理的重要基础资料之一[1]。径流不仅对气候变化的响应十分敏感,还受到水库调蓄、植被覆盖变化、工农业用水等人类活动的影响[2],实现变化环境下流域径流的准确模拟对合理开发和优化配置水资源、更好地制定区域社会经济规划有着重要意义[3]。目前,流域径流模拟主要依赖于水文模型,但其精度受输入数据、状态变量、模型参数等因素影响。
数据同化作为一种能够实现多源数据融合的方法,能够不断引入观测数据校正模型参数、状态变量等信息,从而提高模型的模拟精度[4],其在水文模拟与预报中的应用多集中在同化径流、土壤湿度、蒸散发等水文变量上[5]。许多学者研究了径流和土壤湿度等基础水文变量的同化,发现仅进行径流或土壤湿度同化能够有效估计模型状态变量与参数,进而提高流域水文模型的径流模拟与预测能力[6-8]。蒸散发作为降雨-径流过程中的中间变量,需要将其与土壤湿度等状态变量建立联系后才能进行同化实验[5, 9]。例如Yin等[10]、Zou等[11]先后利用分布式时变增益水文模型构建了显式蒸散发同化关系,发现蒸散发数据同化能对流域蒸散发进行更准确的估算,同时也能提高径流模拟精度。对于不适合构建蒸散发显式同化关系的模型,王卫光等[12]构建了基于新安江模型的蒸散发隐式同化方案,结果显示同化后径流模拟效果显著改善。目前,国内外许多数据同化实验通常采用遥感产品作为观测数据来讨论径流[13-15]、土壤湿度[16-18]和蒸散发[10-12]在径流模拟与预测中所起到的作用,但针对其时空分辨率对土壤湿度、蒸散发等水文变量同化的影响研究尚有不足。此外,在同化过程中考虑水文模型参数时变能够很好地反映流域特征条件变化[19-21],但对于在蒸散发同化中考虑其相关参数时变的研究较少,且同化实验主要针对单一水文变量,系统考虑多源数据同化及不同组合情景对径流模拟的影响研究有待完善。
因此,本文采用集合卡尔曼滤波方法构建基于新安江模型的数据同化框架,选取遥感蒸散发产品、实测径流为观测数据,对模型模拟的实际蒸散发、径流进行同化。基于上述同化框架,以我国南方湿润地区赣江流域开展实例研究,考虑不同时间分辨率的遥感蒸散发产品以及与实测径流的组合情景,设计了4种同化方案(DA-ET、DA-ET(K)、DA-ET-Q、DA-ET-Q(K))以及一种对照方案OL,对比分析不同同化方案下模型径流模拟结果与对照方案的差异,从而评估基于新安江模型的数据同化过程中遥感蒸散发产品的时间分辨率、考虑蒸散发相关参数时变与否以及多源数据同化对流域径流模拟(整体过程以及高水部分)的影响。
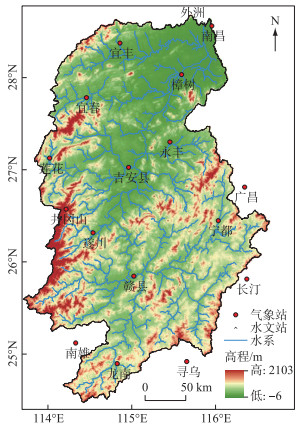
1 数据资料 1.1 流域概况赣江是长江第七大支流,也是江西省境内最大的河流,位于长江中下游南岸(图 1)。赣江流域出口断面外洲水文站以上的控制面积约为8.35万km2,流域地形组成较为复杂,其中山地、低丘、丘陵分别占流域总面积的44%、31%、21%,余下为水域和平原。赣江流域地处亚热带季风气候区,气候湿润,雨量充足,多年平均年降水量约为1540 mm,多年平均年实际蒸发量约为1550 mm,多年平均年径流深约为845 mm。流域年内降水分配不均,约44.33% 的降水集中在4—6月,洪水大多出现在5—7月[22]。
|
图 1 赣江流域位置及水文气象站点分布 Fig.1 Location of the Ganjiang River basin and the hydrometeorological stations |
研究使用的数据包括DEM数据、地面观测数据和遥感蒸散发数据。DEM数据来自于地理数据云平台的SRTMDEM 90 m分辨率高程数据[23]。
地面观测数据包括流量、降水、蒸发皿蒸发。其中流量资料来源于水文年鉴外洲水文控制站的实测日流量数据。降水、蒸发皿蒸发来源于中国气象数据网(http://data.cma.cn/)上赣江流域内及其附近16个气象站点(图 1)的实测数据。
遥感蒸散发数据为Penman-Monteith-Leunin(PML)蒸散发产品,它包括两个版本:PML-V1[24]和PML-V2[25]。PML-V1产品是基于PML模型开发得到的,其时间分辨率为月,空间分辨率为0.05°,来源于http://doi.org/10.4225/08/5719A5C48DB85;PML-V2产品在PML模型的基础上,考虑了植被蒸腾与总初级生产力的相互制约,其时间分辨率为8 d,空间分辨率为0.05°,来源于国家青藏高原科学数据中心(http://data.tpdc.ac.cn/zh-hans/)。
由于所得实测日流量资料仅到2010年,同时考虑到降水、蒸发皿蒸发以及遥感蒸散发数据与径流数据在时间序列上的统一,以及上述数据在2000—2010年之间的数据质量,故选取2000—2010年作为本研究的数据时间序列。此外,根据水文模型输入数据要求,流域面平均降水和面平均蒸发皿蒸发采用泰森多边形方法计算得到。流域面平均实际蒸散发则基于PML蒸散发产品,采用ArcGIS栅格数据处理工具集与栅格属性工具集中的裁剪与获取栅格属性工具计算得到。
2 研究方法 2.1 新安江模型新安江(XAJ)模型是原华东水利学院赵人俊教授提出的1种概念性集总式水文模型,该模型已广泛应用于我国湿润、半湿润地区的径流模拟与预报中[26]。模型主要包括蒸散发、产流、分水源和汇流计算4部分,其中蒸散发采用三层蒸发模型计算,产流通过蓄满产流计算,水源划分采用三水源划分,河网汇流采用了滞后演算法[26]。模型参数的物理意义与参考取值范围见表 1。
| 表 1 新安江模型参数简介及其参考取值范围 Tab. 1 Description of the parameters of the XAJ model |
模型在蒸散发计算时,根据土壤垂直分布特性将土壤分为3层,每层对应的张力水容量分别为WUM(上层张力水容量)、WLM(下层张力水容量)、WDM(深层张力水容量),然后依次计算每层的蒸散发量EU(上层蒸散发量)、EL(下层蒸散发量)、ED(深层蒸散发量), 最终累加得到E(总蒸散发量)。
2.2 集合卡尔曼滤波集合卡尔曼滤波(EnKF)是一种基于卡尔曼滤波理论和蒙特卡洛估计方法的顺序数据同化技术[11]。它通过引入集合概念与蒙特卡洛方法,具有稳健、灵活、易于实现、能够在非线性系统进行应用等优点。其状态转移方程和观测方程为:
| (θfi,tXfi,t)=(θai,t−1f(Xai,t−1,θfi,t))+(εω),ε∼N(0,Q),ω∼N(0,R) | (1) |
| Yi,t=h(Xfi,t,θfi,t)+η,η∼N(0,S) | (2) |
式中,θ为参数变量,X为状态变量,Y为模拟的观测变量;θi, t-1a、Xi, t-1a是t-1时刻第i个集合的分析值;θi, tf、Xi, tf是t时刻第i个集合的预测值;Yi, t为t时刻第i个集合的模拟值;f、h分别表示模型算子与观测算子;ε、ω、η分别为参数、模型、观测误差,服从均值为0,特定方差为(Q,R,S)的正态分布。
当获得t时刻的观测数据时,更新过程:
| (θai,tXai,t)=(θfi,tXfi,t)+(Kθt[Yt−h(Xfi,t,θfi,t)]KXt[Yt−h(Xfi,t,θfi,t)]) | (3) |
式中,Yt为t时刻的观测变量;Kt是卡尔曼增益矩阵,其计算方法详见参考文献[28]。
2.3 基于新安江模型的同化框架构建本文采用新安江模型作为模型算子,遥感蒸散发产品与实测径流作为观测数据,模型中的3层土壤张力水蓄水量(WU、WL、WD)作为状态变量,利用集合卡尔曼滤波构建了基于新安江模型的同化框架(图 2)。

|
图 2 基于新安江模型的数据同化框架 Fig.2 Data assimilation framework based on XAJ model |
同化框架由蒸散发同化与径流同化两部分组成,其中状态变量X为3层土壤张力水蓄量组成的向量M=(WU, WL, WD)T,观测变量为实际蒸散发ET和实测径流Q。由于模型敏感参数较多[29-30],仅依靠观测变量ET和Q对其进行时变更新具有一定不确定性,而蒸散发计算中的敏感参数仅有K,因此,同化框架中的参数变量θ仅考虑为参数K。蒸散发同化的状态方程和观测方程如下,考虑到遥感产品的实际蒸散发为固定时段(逐月或8天)内的均值,故本文设置在t为每个时段末才引入观测数据,此时观测方程变为(6),否则为(5):
| (Kf,ETi,t+1Mf,Q,ETi,t)=(Ka,ETi,tMa,Qi,t)+(εω) | (4) |
| ETi,t=h(Mf,Q,ETi,t,Kf,ETi,t)+η | (5) |
| ETi,t=t∑t=nh(Mf,Q,ETi,t,Kf,ETi,t)+ηn | (6) |
式中,n表示时段内所含的天数,Ki, t+1f, ET表示在ET同化时,t+1时刻第i个集合的预测值;Ki, ta, ET表示经ET同化后,t时刻第i个集合的分析值;Mi, tf, Q, ET表示Q同化完成后进行ET时,t时刻第i个集合的预测值;Mi, ta, Q表示经Q同化后,t时刻第i个集合的分析值;h表示新安江模型。
径流同化的状态方程和观测方程为:
| (Kf,Qi,t+1Mf,Qi,t+1)=(Ka,Qi,tf(Ma,Q,ETi,t))+(εω) | (7) |
| Qi,t=h(Ma,Q,ETi,t,μ)+η | (8) |
式中,Ki, t+1f, Q表示在Q同化时,t+1时刻第i个集合的预测值;Ki, ta, Q表示经ET同化后,t时刻第i个集合的分析值;Mi, t+1f, Q表示在Q同化时,t+1时刻第i个集合的预测值;Mi, ta, Q, ET表示经Q、ET同化后,t时刻第i个集合的分析值;μ表示与产汇流相关的模型参数;f表示新安江模型。
基于此同化框架,设计了4种不同同化方案(DA-ET、DA-ET(K)、DA-ET-Q、DA-ET-Q(K))以及1种对照方案OL(表 2)。其中OL方案作为对照,仅考虑状态变量预测过程且参数为常数,不对状态变量与参数进行更新[31];DA-ET方案考虑了状态变量预测过程且参数为常数,利用遥感蒸散发产品更新状态变量;DA-ET(K)方案同时考虑了状态变量预测过程和参数(K)时变过程,利用遥感蒸散发产品更新状态变量与参数(K);DA-ET-Q方案考虑了状态变量预测过程且参数为常数,利用遥感蒸散发产品与实测径流先后更新状态变量;DA-ET-Q(K)方案同时考虑了状态变量预测过程和参数(K)时变过程,先利用遥感蒸散发产品更新状态变量,后利用实测径流更新状态变量与参数(K)。考虑到多变量同时同化已被应用于径流模拟方面并能有效改善径流模拟效果[32-33],但Xiong等[28]研究表明先后同化ET、Q与同时同化ET、Q所得结果无显著差异,且本文设计DA-ET-Q方案旨在探究在同化ET的基础上再加入Q进行同化能否进一步改善模型径流模拟效果,故本文设置DA-ET-Q方案开展多源数据同化研究。此外,参考以往研究,选取同化实验的集合数N为30[12],参数、模型状态与观测变量误差分别设定为1%、5% 和15% [15]。
| 表 2 基于新安江模型数据同化框架下的不同同化方案 Tab. 2 Description of the designed data assimilation scenarios based on the XAJ model |
选用了3个指标来评价模型在不同同化方案下的径流模拟效果,其中纳什系数(NSE)、均方根误差(RMSE)用来评价径流整体的模拟效果,相关系数(r)用来评价径流高水部分(验证期内前10% 的日径流作为径流高水部分)的模拟效果。各指标计算公式如下[34-36]:
| NSE=1−n∑i=1(Qsim,t−Qobs,t)2n∑i=1(Qobs,t−ˉQobs)2 | (9) |
| RMSE=√n∑i=1(Qsim,t−Qobs,t)2n | (10) |
| r=m∑i=1(Q10%obs,i−ˉQ10%obs)(Q10%sim,i−ˉQ10%sim)√m∑i=1(Q10%obs,i−ˉQ10%obs)2×n∑i=1(Q10%sim,i−ˉQ10%sim)2 | (11) |
式中,
NSE、r越接近1,RMSE越小,说明模型径流模拟效果越好,反之越差。
3 结果分析 3.1 新安江模型的率定与验证本研究以模拟径流与实测径流的误差最小为目标函数,选取2000—2007年为模型率定期,2008—2010年为验证期,利用SCE-UA算法[37]通过流域外洲水文控制站的实测流量对模型进行参数率定(表 3)。
| 表 3 赣江流域新安江模型的参数率定结果 Tab. 3 Parameter estimations of the XAJ model calibrated in Ganjiang River Basin |
图 3展示了模型在率定与验证期的径流模拟结果,其中率定期NSE为0.8888,验证期NSE为0.9261,均在0.85以上;RMSE分别为626.83和951.98 m3/s。模型在率定期与验证期均方根误差均较大,主要是由于模型在高流量时的模拟值偏低。此外,模型验证期相对误差较大,主要由于验证期内2010年夏季出现的洪水洪量偏大,但率定期出现过与验证期内相同量级的洪水,因此,在进行参数率定时已将洪水造成的模拟影响考虑在内。从总体上看,新安江模型在赣江流域的径流模拟效果较为合理,能够用于下一步数据同化计算。

|
图 3 新安江模型在率定期(2000—2007年)与验证期(2008—2010年)的径流模拟结果 Fig.3 Observed and simulated streamflow by the XAJ model during the calibration period (2000-2007) and validation period (2008-2010) |
表 4展示了验证期(2008—2010年)内模型在OL方案下运行的结果。其NSE和RMSE分别为0.8903和794.05 m3/s,相较于采用SCE-UA算法估计参数的方案下的径流模拟结果,NSE略微下降,但RMSE有所改善。总之,OL运行方案不会引起模型的显著偏差和劣化,可用于同化后模型结果的对比分析。
| 表 4 验证期(2008—2010年)内OL和DA-ET方案下的模型径流模拟结果 Tab. 4 Comparison of streamflow simulations under the OL and DA-ET scenarios during the validation period (2008-2010) |
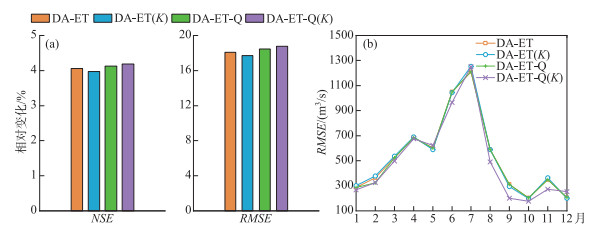
表 4展现了在DA-ET方案下,分别同化两种不同时间分辨率的遥感蒸散发产品后模型所得结果。可以看出模型在同化两种遥感蒸散发产品后所得的RMSE均有所减小,且对于采用SCE-UA估计参数的方案RMSE降低了约290 m3/s;但对NSE的改善程度很小,尤其对比采用SCE-UA估计参数的方案,模型在同化PML-V1产品后所获得的NSE略微降低。图 4a进一步展示了模型在同化两种遥感蒸散发产品后相较于OL方案下的相对变化,可以发现同化两种产品对模型NSE的提高均在4% 左右,而RMSE显著减小,且同化PML-V2产品后的减小幅度要大于PML-V1,即PML-V2产品的同化效果要优于PML-V1。这表明遥感蒸散发产品的时间分辨率对同化结果有一定影响,时间分辨率越高意味着可用的观测数据越多,这增加了模型校正频率从而提高了径流模拟精度,与Azimi等[16]在对土壤湿度产品进行同化中得到的结论一致。

|
图 4 验证期(2008—2010年)内DA-ET方案与OL方案下的径流模拟结果对比:(a)NSE与RMSE的相对变化;(b)月平均RMSE值 Fig.4 Comparison of streamflow simulations under the OL and DA-ET scenarios in validation period (2008-2010): (a) the relative changes of Nash-Sutcliffe index (NSE) and root mean square error (RMSE); (b) the monthly mean RMSE values |
图 4b展示了验证期内,模型在DA-ET与OL方案下所得径流的月平均RMSE。可以看出在DA-ET方案下,两种产品的同化表现在2月差异较大,模型在同化PML-V2产品后所得月平均RMSE约为360 m3/s,远远低于同化PML-V1产品与OL方案。在其余月份,两种产品的同化效果基本一致。此外,RMSE改善主要集中在丰水期(3—7月),其中4—6月内RMSE的改善十分明显,这说明模型状态变量在丰水期变化较大,且同化后能合理地模拟状态变量的变化过程,而在枯水期(8、9、11月)的RMSE有所增加。总体上看,经两种蒸散发产品同化后模型整体的径流模拟效果有所提升,且在丰水期的表现更加明显,而在枯水期模拟精度有所降低。
3.2.2 蒸散发相关参数时变与多源数据同化对同化的影响表 5展现了模型在均使用PML-V2产品的基础上,分别进行DA-ET、DA-ET(K)、DA-ET-Q、DA-ET-Q(K)四种同化方案所得径流模拟结果。可以发现,对比DA-ET方案,3种方案对径流模拟效果的改善不明显,甚至在DA-ET(K)方案下,模型模拟径流的NSE、RMSE略微变差。
| 表 5 验证期(2008—2010年)内不同同化方案下模型的径流模拟结果 Tab. 5 Comparison of streamflow simulated under different data assimilation scenarios during the validation period (2008-2010) |
图 5a进一步展示了4种方案相较于OL方案下模型模拟径流NSE与RMSE的相对变化。可以看出,4种方案NSE提高程度均在4% 左右,RMSE改善程度均在18% 左右,但DA-ET-Q(K)方案下的径流模拟精度略高于其他3种方案。图 5b展示了验证期内,模型在4种方案下所得径流的月平均RMSE,可以发现DA-ET-Q(K)方案在8—11月所得月平均RMSE低于其余方案,说明DA-ET-Q(K)方案对径流模拟的改善主要集中在8—11月,而其余方案所得月平均RMSE的差异并不明显。总体上看,在同化ET的基础上,同时考虑蒸散发相关参数K时变与加入径流进行多源同化(DA-ET-Q(K))对模型径流模拟的NSE、RMSE改善效果最好,但4种同化方案的差异并不明显。部分原因是模型在DA-ET方案下所得NSE已十分接近1,导致模型径流模拟效果进一步提高的空间有限且难度较大,但这对改善模型表现较差地区的径流精度具有重要意义。
|
图 5 验证期(2008—2010年)内4种同化方案与OL方案下的径流模拟结果对比:(a)NSE与RMSE的相对变化;(b)月平均RMSE值 Fig.5 Comparison of streamflow simulations under the OL and four data assimilation scenarios in validation period (2008-2010): (a) the relative changes of Nash-Sutcliffe index (NSE) and root mean square error (RMSE); (b) the monthly mean RMSE values |
由于参数K影响模型的水量平衡,本文进一步计算了模型在4种方案下的径流相对误差,发现4种方案得到的径流相对误差分别为4.41%、3.38%、4.35%、3.43%。可见在同化蒸散发的基础上,无论是考虑参数时变还是加入径流进行多源同化,径流相对误差均减小。但DA-ET-Q方案的减幅仅为1.36%,而DA-ET(K) 与DA-ET-Q(K)方案下的减幅分别高达23.46% 与22.28%。这表明在同化过程中将参数进行同步估计能较好的反映流域特征条件变化,进而减小径流模拟的相对误差,与Sahani等[20]的研究结论一致。
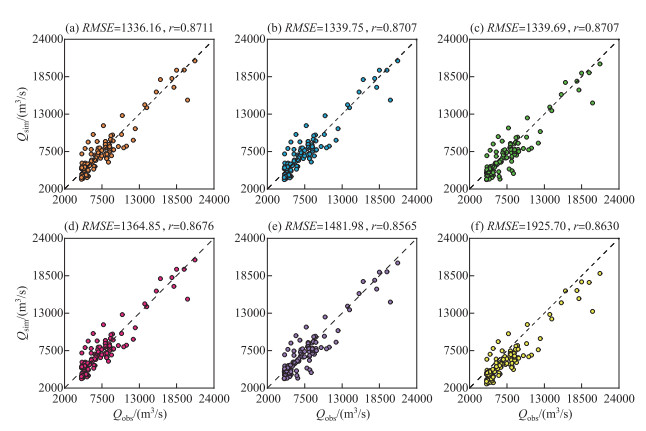
3.3 不同同化方案对径流高水部分模拟的影响图 6总结了4种同化方案及1种对照方案(共6个同化实验)在验证期内对径流高水部分的模拟结果,其中a~f分别代表的是DA-ETPML-V1、DA-ETPML-V2、DA-ETPML-V2-Q、DA-ETPML-V2(K)、DA-ETPML-V2-Q (K)、OL。可以发现,虽然DA-ETPML-V2-Q (K)方案能够有效降低模型对径流高水部分模拟的RMSE,但相关系数r却有所下降。而其余方案差异相对较小,所得平均RMSE相比OL方案大约减小了600 m3/s,相关系数r大约提高了0.07。从总体上看,同化后模型对径流高水部分模拟的精度均有所提高,DA-ETPML-V1(RMSE=1336.16 m3/s) 表现最好,其次是DA-ETPML-V2-Q与DA-ETPML-V2(二者的RMSE十分接近,约为1339 m3/s),最后是DA-ETPML-V2(K)与DA-ETPML-V2-Q (K)(RMSE分别为1364.85与1481.98 m3/s)。
|
图 6 验证期(2008—2010年)内不同同化方案下模型径流高水部分的模拟结果:(a)DA-ETPML-V1;(b)DA-ETPML-V2;(c)DA-ETPML-V2-Q;(d)DA-ETPML-V2(K);(e)DA-ETPML-V2-Q(K);(f)OL Fig.6 Comparison of 10% highest streamflow simulated under different data assimilation scenarios during the validation period (2008-2010): (a) DA-ETPML-V1; (b) DA-ETPML-V2; (c) DA-ETPML-V2-Q; (d)DA-ETPML-V2(K); (e)DA-ETPML-V2-Q (K); (f) OL |
本文采用集合卡尔曼滤波算法,构建了基于新安江模型的数据同化框架并设计了4种不同同化方案(DA-ET、DA-ET(K)、DA-ET-Q、DA-ET-Q(K))以及1种对照方案OL,探讨了基于新安江模型的数据同化过程中遥感蒸散发产品的时间分辨率、考虑蒸散发相关参数时变与否以及多源数据同化对径流模拟结果的影响。主要结论如下:
1) 分别同化两种遥感蒸散发产品均能提高模型整体的径流模拟精度,但同化PML-V2产品后模型径流模拟精度要优于PML-V1,可见时间分辨率更高的产品对同化后径流模拟效果的改善显著。
2) 4种同化方案所得径流NSE、RMSE十分相近,但在同化ET的基础上考虑加入Q进行多源数据同化的效果更好,且在同化过程中考虑蒸散发参数K时变能够有效降低径流的相对误差。
3) 相比对照方案OL,4种同化方案均能有效改善模型对径流高水部分的模拟能力,而其余3种方案的改善效果优于DA-ET-Q(K)方案,且RMSE均减小了约600 m3/s。
本文的研究表明,在蒸散发同化过程中使用更高时间分辨率的蒸散发产品、考虑蒸散发相关参数时变以及引入实测径流进行多源数据同化均能提高径流模拟效果。为了充分利用现有站点数据和遥感数据,在未来研究中可考虑使用通量站实测蒸散发数据对蒸散发同化结果进行验证与分析,或同化具有更高空间分辨率的产品以提高径流模拟精度。另外,如何尽可能减小水文模型参数率定过程中的不确定性以及同化过程中参数估计和状态预测的不确定性对同化结果的影响,还需要后续深入研究。
| [1] |
Bao ZX, Zhang JY, Yan XL et al. Quantitative assessment of the attribution of runoff change caused by four factors in the Haihe River basin. Advances in Water Science, 2021, 32(2): 171-181. [鲍振鑫, 张建云, 严小林等. 基于四元驱动的海河流域河川径流变化归因定量识别. 水科学进展, 2021, 32(2): 171-181. DOI:10.14042/j.cnki.32.1309.2021.02.002] |
| [2] |
Liu CZ, Zhan CS, Xia J et al. Review on the influences of climate change and human activities on runoff. Journal of Hydraulic Engineering, 2014, 45(4): 379-385. [刘春蓁, 占车生, 夏军等. 关于气候变化与人类活动对径流影响研究的评述. 水利学报, 2014, 45(4): 379-385. DOI:10.13243/j.cnki.slxb.2014.04.001] |
| [3] |
Liu JY, Zhang Q, Singh VP et al. Contribution of multiple climatic variables and human activities to streamflow changes across China. Journal of Hydrology, 2017, 545: 145-162. DOI:10.1016/j.jhydrol.2016.12.016 |
| [4] |
Lei XH, Wang H, Liao WH et al. Advances in hydro-meteorological forecast under changing environment. Journal of Hydraulic Engineering, 2018, 49(1): 9-18. [雷晓辉, 王浩, 廖卫红等. 变化环境下气象水文预报研究进展. 水利学报, 2018, 49(1): 9-18. DOI:10.13243/j.cnki.slxb.20170750] |
| [5] |
Liu YW, Wang WG, Liu YB et al. Advances in multi-source data assimilation approach and application in simulation and forecast of hydrological model. Journal of Hohai University: Natural Science, 2021, 49(6): 483-491. [刘永伟, 王文, 刘元波等. 水文模型模拟预报的多源数据同化方法及应用研究进展. 河海大学学报: 自然科学版, 2021, 49(6): 483-491.] |
| [6] |
Yuan L, Stefania G, Jeffrey PW et al. Application of remote sensing data to constrain operational rainfall-driven flood forecasting: A review. Remote Sensing, 2016, 8(6): 456. DOI:10.3390/rs8060456 |
| [7] |
Meng SS, Xie XH, Liang SL. Assimilation of soil moisture and streamflow observations to improve flood forecasting with considering runoff routing lags. Journal of Hydrology, 2017, 550: 568-579. DOI:10.1016/j.jhydrol.2017.05.024 |
| [8] |
Deng C, Liu P, Wang WG et al. Modelling time-variant parameters of a two-parameter monthly water balance model. Journal of Hydrology, 2019, 573: 918-936. DOI:10.1016/j.jhydrol.2019.04.027 |
| [9] |
Zhan CS, Dong QQ, Ye W et al. A review on evapotranspiration data assimilation based on hydrological model. Acta Geographica Sinica, 2015, 70(5): 809-818. [占车生, 董晴晴, 叶文等. 基于水文模型的蒸散发数据同化研究进展. 地理学报, 2015, 70(5): 809-818.] |
| [10] |
Yin J, Zhan CS, Ye W. An experimental study on evapotranspiration data assimilation based on the hydrological model. Water Resources Management, 2016, 30(14): 5263-5279. DOI:10.1007/s11269-016-1485-5 |
| [11] |
Zou L, Zhan CS, Xia J et al. Implementation of evapotranspiration data assimilation with catchment scale distributed hydrological model via an ensemble Kalman Filter. Journal of Hydrology, 2017, 549: 685-702. DOI:10.1016/j.jhydrol.2017.04.036 |
| [12] |
Wang WG, Li JX, Wei JD et al. Runoff simulation by hydrological model based on the assimilated evapotranspiration. Advances in Water Science, 2018, 29(2): 159-168. [王卫光, 李进兴, 魏建德等. 基于蒸散发数据同化的径流过程模拟. 水科学进展, 2018, 29(2): 159-168. DOI:10.14042/j.cnki.32.1309.2018.02.002] |
| [13] |
Lopez LP, Wanders N, Schellekens J. Improved large-scale hydrological modelling through the assimilation of streamflow and downscaled satellite soil moisture observations. Hydrology and Earth System Sciences, 2016, 20(7): 3059-3076. DOI:10.5194/hess-20-3059-2016 |
| [14] |
Wang S, Huang GH, Baetz BW et al. Examining dynamic interactions among experimental factors influencing hydrologic data assimilation with the ensemble Kalman filter. Journal of Hydrology, 2017, 554: 743-757. DOI:10.1016/j.jhydrol.2017.09.052 |
| [15] |
Sun Y, Bao W, Valk K et al. Improving forecast skill of lowland hydrological models using Ensemble Kalman Filter and Unscented Kalman Filter. Water Resources Research, 2020, 56(8): e2020W-e27468W. |
| [16] |
Azimi S, Dariane AB, Modanesi S et al. Assimilation of Sentinel 1 and SMAP-based satellite soil moisture retrievals into SWAT hydrological model: the impact of satellite revisit time and product spatial resolution on flood simulations in small basins. Journal of Hydrology, 2020, 581: 124367. DOI:10.1016/j.jhydrol.2019.124367 |
| [17] |
Santis DD, Biondi D, Crow WT et al. Assimilation of satellite soil moisture products for river flow prediction: An extensive experiment in over 700 catchments throughout Europe. Water Resources Research, 2021, 57(6): e2021W-e29643W. |
| [18] |
Nayak AK, Biswal B, Sudheer KP. Role of hydrological model structure in the assimilation of soil moisture for streamflow prediction. Journal of Hydrology, 2021, 598: 126465. DOI:10.1016/j.jhydrol.2021.126465 |
| [19] |
Xiong MS, Liu P, Deng C. Identifying functional form of time-varying hydrological model parameters under changing environment. Journal of Water Resources Research, 2018, 7(4): 351-359. [熊梦思, 刘攀, 邓超. 变化环境下水文模型时变参数的识别及函数型式构建. 水资源研究, 2018, 7(4): 351-359.] |
| [20] |
Sahani P, Daniela A, Paolo B et al. Time-varying parameter models for catchments with land use change: the importance of model structure. Hydrology and Earth System Sciences, 2018, 22(5): 2903-2919. DOI:10.5194/hess-22-2903-2018 |
| [21] |
Zhang XJ, Liu P. A time-varying parameter estimation approach using split-sample calibration based on dynamic programming. Hydrology and Earth System Sciences, 2021, 25(2): 711-733. DOI:10.5194/hess-25-711-2021 |
| [22] |
Zhang YQ, You QL, Lin HB et al. Analysis of dry/wet conditions in the Gan River Basin, China, and their association with large-scale atmospheric circulation. Global and Planetary Change, 2015, 133: 309-317. DOI:10.1016/j.gloplacha.2015.09.005 |
| [23] |
Reuter HI, Nelson A, Jarvis A. An evaluation of void-filling interpolation methods for SRTM data. International Journal of Geographical Information Science, 2007, 9(21): 983-1008. |
| [24] |
Zhang YQ, Peña-Arancibia JL, Mcvicar TR et al. Multi-decadal trends in global terrestrial evapotranspiration and its components. Scientific Reports, 2016, 6(1): 19124. DOI:10.1038/srep19124 |
| [25] |
Zhang YQ, Kong DD, Gan R et al. Coupled estimation of 500 m and 8-day resolution global evapotranspiration and gross primary production in 2002-2017. Remote Sensing of Environment, 2019, 222: 165-182. DOI:10.1016/j.rse.2018.12.031 |
| [26] |
Zhao RJ. The Xinanjiang model applied in China. Journal of Hydrology, 1992, 135(1/2/3/4): 371-381. |
| [27] |
Lu MJ. Recent and future studies of the Xinanjiang Model. Journal of Hydraulic Engineering, 2021, 52(4): 432-441. [陆旻皎. 新安江模型研究的回顾和展望. 水利学报, 2021, 52(4): 432-441.] |
| [28] |
Xiong MS, Liu P, Cheng L et al. Identifying time-varying hydrological model parameters to improve simulation efficiency by the ensemble Kalman filter: A joint assimilation of streamflow and actual evapotranspiration. Journal of Hydrology, 2019, 568: 758-768. |
| [29] |
Zhao RJ, Wang PL. Analysis of Xin'anjiang model parameters. Journal of China Hydrology, 1988(6): 2-9. [赵人俊, 王佩兰. 新安江模型参数的分析. 水文, 1988(6): 2-9.] |
| [30] |
Zhao RJ, Wang PL, Hu FB. Relations between parameter values and corresponding natural conditions of Xinanjiang model. Journal of Hohai University, 1992(1): 52-59. [赵人俊, 王佩兰, 胡凤彬. 新安江模型的根据及模型参数与自然条件的关系. 河海大学学报, 1992(1): 52-59.] |
| [31] |
Jafarzadegan K, Abbaszadeh P, Moradkhani H. Sequential data assimilation for real-time probabilistic flood inundation mapping. Hydrology and Earth System Sciences, 2021, 25(9): 4995-5011. |
| [32] |
Xiang YH, Moradkhani H. Combined assimilation of streamflow and satellite soil moisture with the particle filter and geostatistical modeling. Advances in Water Resources, 2016, 94: 364-378. |
| [33] |
Jiang DJ, Wang K. The role of satellite-based remote sensing in improving simulated streamflow: A review. Water, 2019, 11(8): 1615. |
| [34] |
Yin JB, Guo SL, Wang J. Blending multi-source data in hydrological simulations based on BMA method. Journal of Hydraulic Engineering, 2020, 51(11): 1335-1346. [尹家波, 郭生练, 王俊等. 基于贝叶斯模式平均方法融合多源数据的水文模拟研究. 水利学报, 2020, 51(11): 1335-1346.] |
| [35] |
Abro MI, Zhu DH, Khaskheli MA et al. Statistical and qualitative evaluation of multi-sources for hydrological suitability inflood-prone areas of Pakistan. Journal of Hydrology, 2020, 588: 125117. |
| [36] |
Zhang YQ, Chiew FHS, Liu CM et al. Can remotely sensed actual evapotranspiration facilitate hydrological prediction in ungauged regions without runoff calibration?. Water Resources Research, 2020, 56(1): e2019W-e26236W. |
| [37] |
Duan QY, Gupta VK, Sorooshian S. Shuffled complex evolution approach for effective and efficient global minimization. Journal of Optimization Theory and Applications, 1993, 76(3): 501-521. |
 2023, Vol. 35
2023, Vol. 35 


