(2: 河海大学水安全与水科学协同创新中心, 南京 210024)
(3: 南京大学环境规划设计研究院集团股份公司, 南京 210008)
(4: 扬州大学水利科学与工程学院, 扬州 225009)
(5: 苏州科技大学环境科学与工程学院, 苏州 215009)
(2: Cooperative Innovation Center for Water Safety & Hydro Science, Hohai University, Nanjing 210024, P. R. China)
(3: Academy of Environmental Planning & Design Co., Ltd, Nanjing University, Nanjing 210008, P. R. China)
(4: College of Hydraulic Science and Engineering, Yangzhou University, Yangzhou 225009, P. R. China)
(5: School of Environmental Science and Engineering, Suzhou University of Science and Technology, Suzhou 215009, P. R. China)
基于水文模型的洪水预报调度不可避免地存在着模型输入、结构、参数及初始条件等诸多不确定性,使得预报结果具有不确定性[1-2]。近年来,人们对防洪预报调度的可靠性要求逐步提高,追求更高的预报精度和更小的不确定度。实时校正通过获取实时信息,对模型输入、参数、状态变量或预报值等进行合理校正,降低预报误差[3];大体上可以分为过程误差校正(process bias correction, PBC)、终端误差校正(terminal bias correction, TBC)以及两者的综合校正方法。其中,PBC以卡尔曼滤波[4-7]、动态系统响应曲线及其改进[8-12]等方法为代表,以降低预报各环节的误差。温娅惠等[13]分析不同预见期和不同降雨输入情况下实时洪水预报精度的变化;针对复杂河流系统的长河段洪水演进,Huang等[11]和Liang等[12]耦合了马斯京根法矩阵方程与动力系统反演方程,通过降低上游各站点/断面的预报误差,提高下游站点实时洪水预报精度。TBC不考虑过程误差,直接修正预报结果,代表性方法有误差自回归模型[14]、反馈模拟校正和BP神经网络校正[15]等。张琳和王国利[16]分析了不同雨量等级下,洪水预报模型输入误差与输出误差的分布规律及两种误差的相关关系;徐杰等[15]采用反馈模拟算法校正洪水预报精度,取得较好效果。此外,传统的水文预报提供的都是确定性定值预报结果,无法客观评估预报成果的可靠性及风险大小。洪水概率预报不仅能以概率分布的某一分位数(如中位数、期望值等)提供类似于传统确定性预报的定值预报结果,也可以给出不同置信度的区间预报结果,提供更为丰富的预报信息[17]。目前国内外洪水概率预报方法大致可以分为不确定性要素耦合和总误差分析两类途径。比如分析参数不确定性的GLUE方法[18]、分析模型结构不确定性的贝叶斯模型平均法(BMA)[19]以及分析降雨输入、模型结构和参数耦合不确定性的IBUNE方法[20]等,均属于第一类。而第二类途径不直接处理各环节不确定性,代之以处理其总误差,如Todini等[21]提出的模型条件处理器(MCP)、Jiang等[17]和梁忠民等[22]提出的考虑误差异分布的概率预报方法(HRD)等。本质上讲,实时校正和概率预报都是处理洪水预报误差的方式,试图提供更准确、更丰富的成果信息;因此若能将该两种处理方式进行集成,将可能更大程度上改进实时洪水预报精度。
大渡河是岷江最大支流,建有梯级水电站,是我国重要水电清洁能源基地之一,对汛期防洪发电调度决策的可靠性要求较高,有定量评估风险的现实需求。因此,本文选择大渡河干流第一梯级水电站猴子岩水库入库洪水预报为研究对象,构建集成洪水过程预报-实时误差校正-概率预报于一体的技术体系,提高入库洪水过程的确定性预报精度,定量分析预报不确定性,提供概率预报成果,为水库发电调度和风险管理提供科学支撑。
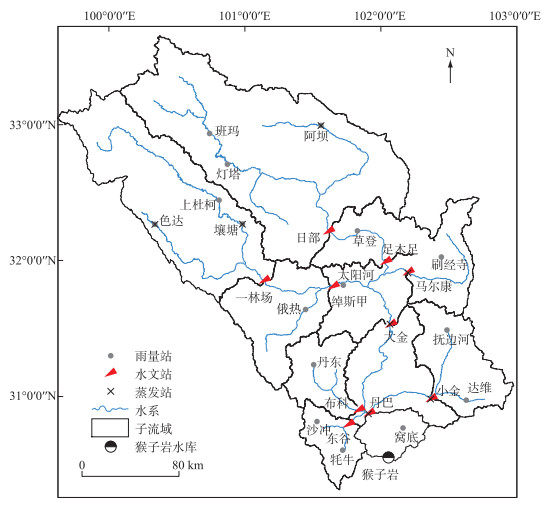
1 研究区域及数据说明 1.1 研究区域大渡河是长江上游一级支流岷江的最大支流,流域内高山耸峙,河流深切,沟谷深邃,平均海拔介于1600~6100 m之间,水力资源丰富,建有梯级水电站。其中,猴子岩水库是干流第一级水电站,水库以上集水面积为54221 km2,占大渡河流域总面积的70 %。流域属于川西高原气候区,多年平均降水量为700 mm左右,在空间上雨区呈多中心分布,在时间上多集中在6—9月。研究区域内共有16个雨量站、10个水文站(其中,足木足、绰斯甲、大金、丹巴4站同时观测蒸发皿蒸发),研究区地理位置及站网分布如图 1所示。
|
图 1 猴子岩水库以上流域水系、站网分布及子流域划分示意图 Fig.1 Schematic diagram of river, station network and sub-basins in the watershed above Houziyan Reservoir |
所用资料包括2009年1—12月、2020年6—10月的逐小时实测降水和流量资料,以及2009—2014年的逐日蒸发皿蒸发资料。缺测的2015—2020年的蒸发数据采用2009—2014年的多年平均逐日蒸发值替代,次洪模型所需的逐小时蒸发数据采取日蒸发量的小时平均值。考虑到场次洪水历时不长,雨期蒸发在次洪水量平衡中贡献较小,对应的资料处理误差可以接受。
2 研究方法 2.1 新安江次洪模型猴子岩流域属于川西高原气候区,在上游靠近河源部分虽然常年温度较低,基本在6℃以下,存在较多的融雪径流,但根据2009—2019年降水径流资料统计,流域多年平均年径流系数为0.68,多年平均降水量约700 mm。因此流域内大部分地区还是属于半湿润地区,相较于其他的水文模型,基于蓄满产流模式的新安江模型在理论上更为适用。
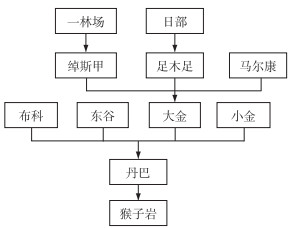
采用三水源新安江模型开展确定性次洪过程预报,模型原理和方法可参见文献[23]。以自然分水岭为边界、各水文站为出口,将整个流域划分为11个子流域,各子流域的拓扑关系如图 2所示,建立分散式新安江次洪模型。其中,各子流域内河网汇流采用滞后演算法,各子流域出口至猴子岩入库的河道汇流采用分段马斯京根连续演算法。
|
图 2 研究区各子流域拓扑关系示意 Fig.2 Schematic diagram of the topological relationship of each sub-basin in the study area |
采用包为民团队提出的动态系统响应曲线校正技术(dynamic system response curve, DSRC)[8-10]对实时洪水预报误差校正,提高预报精度。该技术将预报模型视为输入变量与输出预报值的响应系统,建立系统响应矩阵,根据输出误差修正输入变量后,再重新驱动预报模型,最终得到校正后的预报流量。考虑到预报结果受到输入变量(主要为降雨P)和模型参数θ两类因素影响,因此,t时刻的预报流量Q(t)的响应系统可表达为:
| $ Q(t)=f(P(t), \theta) $ | (1) |
式中,Q=[Q1, Q2, Q3, …, Qn]T为流域出口断面流量过程(m3/s);P= [P1, P2, P3, …, Pm]T为流域降雨系列(mm);n为流量系列长度,m为降雨系列长度,n≥m。模型参数在一定时间内不发生改变,因此,可只考虑输入降雨资料导致的预报误差;省略参数θ,式(1)可简化为所谓的降雨动态系统响应曲线Q(P)=f(P),即将某时段的降雨增加一个单位值所导致的模型计算流量之差值。将输入降雨作为自变量对式(1)求微分,并代入观测流量系列,得到矩阵表达式:
| $ Q(P) \approx Q_{\mathrm{c}}\left(P_{\mathrm{o}}\right)+U \Delta P+W $ | (2) |
式中,Q(P)为实时修正后的计算流量系列(m3/s);Qc(Po)为根据实测降雨系列Po计算得到的流量系列(m3/s);ΔP为待求解的降雨系列误差(mm);W为实时修正后的预报系统残差(m3/s);U为系统响应矩阵,可表示为:
| $ U=\left[\begin{array}{ccc} \frac{\partial Q_1(P)}{\partial P_1} & \cdots & \frac{\partial Q_1(P)}{\partial P_m} \\ \frac{\partial Q_2(P)}{\partial P_1} & \cdots & \frac{\partial Q_2(P)}{\partial P_m} \\ \cdots & \cdots & \cdots \\ \frac{\partial Q_n(P)}{\partial P_1} & \cdots & \frac{\partial Q_n(P)}{\partial P_m} \end{array}\right] $ | (3) |
根据历史雨洪资料可求解式(3),则利用最小二乘法计算得到降雨系列误差ΔP和修正后的新降雨系列PU:
| $ \Delta P=\left(U^T U\right)^{-1} U^T\left(Q_{\mathrm{o}}-Q_{\mathrm{c}}\right) $ | (4) |
| $ P_{\mathrm{U}}=P_{\mathrm{o}}+\Delta P $ | (5) |
式中,Qo为实测流量系列。将PU代入模型重新计算即可得到修正后的流量值。
2.3 水文不确定性处理器(HUP)介绍贝叶斯预报系统(Bayesian forecasting system, BFS)[24-25]将水文预报中的总不确定性分为降雨不确定性以及除此之外的其他所有不确定性(即水文不确定性)两类。BFS包括降雨不确定性处理器(PUP)、水文不确定性处理器(HUP)和集成器(INT)3个模块;其中,HUP是BFS中处理预报不确定性的核心部分。
HUP不分开处理降雨-径流过程各个环节的主要不确定性,而是直接分析水文预报模拟系列和实测系列之间总误差,估计预报变量的后验分布,从而实现预报变量的概率预报[22]。它可以定量分析除输入以外的其它水文要素的不确定性,因结构清晰,计算便捷而广泛应用于国内外洪水概率预报[26-27]。基于HUP的概率预报主要是采用线性-正态模型来估计先验密度函数和似然函数,主要计算流程包括[25]:首先将历史上的预报实测值和确定性预报输出值(水位或流量)进行正态分位数转换,成为符合正态分布函数的样本系列;同时,假设转换后的样本系列间服从线性关系,采用线性回归法求得转换空间里的后验密度函数,再将其还原到原始空间,最终求得预报变量(水位或流量)的后验分布解析式。
2.4 精度评价指标模型预报成果包括确定性和不确定性结果两种,其中,基于新安江次洪模型的确定性预报选用洪量相对误差(REvol, %)、洪峰相对误差(REpeak, %)、峰现时间误差(L)和确定性系数(NS)作为目标函数,按国家标准《水文情报预报规范》(GB/T 22482—2008)评定各场次洪水的合格率和精度等级。不确定性预报结果可以采用某一置信区间(通常情况下取90 % 置信区间)的覆盖率CR和离散度CI两种精度指标进行评价[17, 22]。其中,覆盖率CR是某一置信度的预报区间能够覆盖住实测点据的百分比,在置信区间一定的情况下,覆盖率越高,说明置信区间预报值覆盖住实测变量的程度越高,概率预报可靠度越高;离散度DI是指一定置信区间下,其区间预报宽度相对于实测值的宽度水平,又称平均相对带宽。在保证覆盖率较高的条件下,离散度越小说明概率预报可靠度越高,反之亦然。
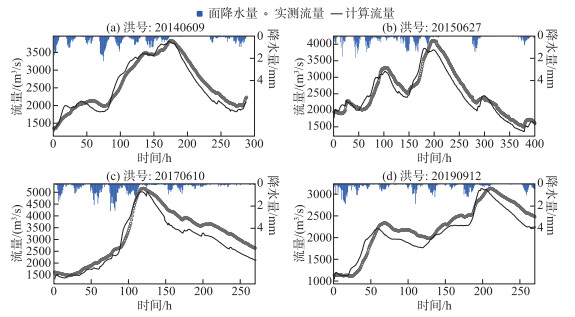
3 结果分析 3.1 次洪模型参数率定与验证以2009—2019年间25场洪水逐小时实测降雨和流量资料进行新安江模型参数的率定与验证。表 1给出各场洪水模拟精度统计结果。其中,前18场和后7场分别用于11个子流域的参数率定和验证。在率定期的18场洪水中,洪量相对误差REvol和洪峰相对误差REpeak均在±20 % 以内,峰现时间误差L均在±3 h以内;其中,多场洪水REvol的平均绝对值为6.65 %,多场洪水REpeak的平均绝对值为4.92 %。从确定性系数指标看,NS < 0.70的有8场,0.70≤NS≤0.90的有8场,NS>0.90的有2场,多场洪水的NS平均值为0.69。在验证期的7场洪水中,REvol和REpeak也均在20 % 以内,其平均绝对值分别为3.64 % 和7.52 %;峰现时间误差L也均在±3 h以内,NS < 0.70的有2场,0.70≤NS≤0.90的有5场,多场洪水的NS平均值为0.72。根据《水文情报预报规范》,以洪量、洪峰和峰现时间的预报误差小于许可误差进行判定,25场洪水均为合格预报,合格率100 %,精度等级为甲等;以确定性系数大小进行判定,甲(NS>0.90)、乙(0.90≥NS≥0.70)、丙(0.70>NS≥0.50)3个等级的洪水场次数分别为2、13和7场。总体上,除3场洪水过程线拟合精度较差外,模型对洪量、洪峰等特征值均有较高的模拟精度,在猴子岩水库流域汛期洪水模拟中具有适用性。图 3给出4场次洪模拟过程线与实测流量点据的对比情况。
| 表 1 猴子岩水库流域次洪率定与验证的精度统计 Tab. 1 Accuracy statistics of flood simulation calibration and validation in Houziyan Reservoir Basin |
|
图 3 猴子岩水库流域4场洪水的计算流量与实测流量过程线对比 Fig.3 Hydrograph comparison between calculated and observed discharges of four floods in Houziyan Reservoir Basin |
动态系统响应曲线校正方法中的响应矩阵代表流量和相应面降雨之间的响应关系,但对于多个子流域组成的较大面积空间,其面降雨量估计将有较大误差,在此基础上应用动态系统响应曲线进行校正也不再适用。因此,仅对研究区11个子流域单元中属于源头和支流的6个子流域(日部、一林场、马尔康、小金、布科、东谷)进行校正,其他子流域直接采用模型计算流量,再通过河道汇流计算得到校正后的猴子岩水库入库洪水过程。
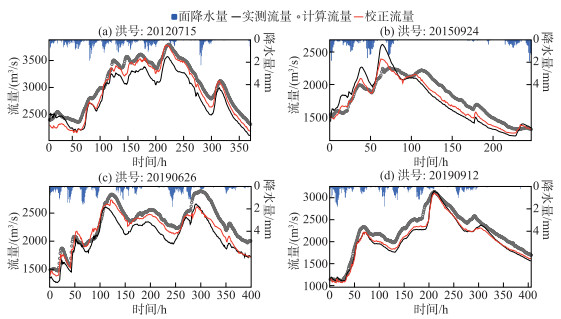
3.2.1 2009—2019年实测降雨驱动的预报校正结果对比表 1中25场洪水模拟结果和校正后的结果,结果表明,率定期的绝大部分场次洪水的REvol和REpeak绝对值均有所降低,REvol平均绝对值由4.92 % 降低到3.90 %,REpeak平均绝对值由6.65 % 降低到5.51 %,NS平均值由0.69提高到0.82;验证期的REvol平均绝对值略有降低(由7.52 % 到7.50 %),NS平均值由0.72提高到0.81,但校正后的REpeak平均绝对值却略有增大(由3.64 % 到3.71 %)。可能原因是由于水文系统的确定性与随机性并存,实时校正技术难以完全控制洪峰、洪量及过程拟合等多方面的精度指标,因而在校正时设定以整体精度提升进行控制。总体上,以洪量、洪峰和峰现时间的预报误差小于许可误差进行判定,场次洪水预报精度仍为甲等(合格率100 %);以确定性系数大小进行判定,甲、乙2个精度等级的洪水场次分别增加到6场和15场,丙级洪水场次为4场,表明实时校正后预报精度得到整体提高。图 4给出猴子岩水库流域4场次洪水实测、计算及校正流量过程线的对比情况。
|
图 4 猴子岩水库流域4场洪水的实测流量、计算流量和校正流量的过程线对比 Fig.4 Hydrograph comparison of measured discharge, calculated discharge and corrected discharge of four floods in Houziyan Reservoir Basin |
总体上,误差校正后大部分场次洪水的洪峰和洪量相对误差有不同程度降低,确定性系数提高幅度较大,过程线更为拟合。与动态系统响应曲线在其他案例中应用比较[8-10],本次校正效果同样较好,整体预报精度得到提高。因此可以说明猴子岩水库流域洪水预报中的面降雨估计是主要不确定性来源之一,通过动态系统响应曲线方法能够有效降低预报模型的输入不确定性[28]。
3.2.2 2020年汛期6—10月预报降雨驱动的预报校正结果根据2020年6—10月未来48 h预报降雨资料,采用动态系统响应曲线校正技术进行未来48 h实时校正预报,检验该校正方法的实际应用效果。同时,采用2020年6—10月的实测降雨资料进行未来48 h校正预报,作为对比平行组试验。选取洪号20200616、20200710和20200811共3场洪水,设置实测降雨、预报降雨驱动两种资料条件以及预见期Δt=1、12、24、48 h 4种情景,对比校正前后精度情况,结果见表 2。
| 表 2 2020年汛期3场洪水校正前后的平均精度对比 Tab. 2 Comparison of average accuracy of three floods before and after correction in 2020 flood season |
由表 2可知,不论是基于预报降雨还是基于实测降雨,3场洪水在校正后,不同预见期的洪峰和洪量相对误差大部分均有所降低,确定性系数得到提高。特别是考虑预报降雨情况下,预见期较长时精度提升幅度大,校正效果更为显著。这与文献[13]的研究结论类似。总体上,该校正方法能够在延长预见期的基础上保证一定的预报精度。
3.3 基于HUP的场次洪水概率预报根据猴子岩流域2009—2019年25场洪水的实测流量和校正后确定性预报流量,估计HUP模型参数,构建基于HUP的概率预报模型,同时应用于2020年6—10月3场洪水概率预报中,定量分析未来48 h次洪预报不确定性。其中,在HUP模型参数估计中,假设流量系列的边际分布服从三参数对数威布尔(Log-Weibull)分布,以时段长为1 h进行未来48 h逐小时的边际分布参数值估计。
3.3.1 2009—2019年实测降雨驱动的洪水概率预报结果以预见期Δt=1 h为例,分析2009—2019年25场洪水概率预报的确定性和不确定性两类精度评估指标。结果表明:①以HUP模型的流量后验分布函数中位数Q50过程线为确定性结果,评估其与实际洪水过程的拟合情况。在率定期18场洪水中,绝大部分洪水Q50的洪峰和洪量相对误差的平均绝对值均在1 % 左右,确定性系数均在0.95左右;在验证期7场洪水中,洪峰和洪量相对误差的平均绝对值分别为1.12 % 和0.99 %,确定性系数平均为0.96,整体预报精度较高。根据《水文情报预报规范》,无论以洪量、洪峰和峰现时间的预报误差小于许可误差还是以确定性系数大小进行判定,25场洪水预报为甲级精度。②以后验分布90 % 置信区间为不确定性结果,率定期和验证期场次洪水的覆盖率指标CR大都在90 % 以上,平均覆盖率分别为93.43 % 和91.85 %,平均离散度均为0.19;可见在90 % 置信区间覆盖率较高的情况下,区间离散度也较低。总体上,不论确定性还是不确定性精度评估指标,预见期为1 h的洪水概率预报的精度均较高。
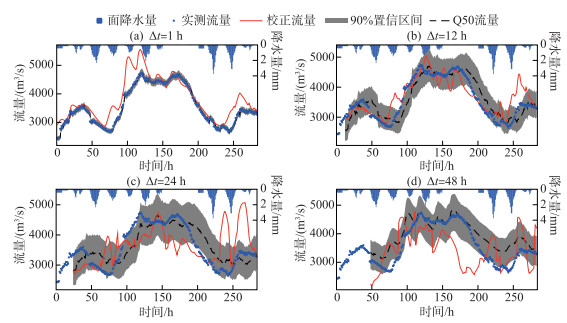
3.3.2 2020年汛期6—10月预报降雨驱动的洪水概率预报结果根据未来48 h的实时校正确定性预报结果(以预报降雨为输入),驱动HUP模型得到相应的概率预报结果;以预见期Δt=1、12、24和48 h为例,分析2010年汛期3场洪水概率预报的确定性和不确定性两类精度评估指标,见表 3。可以看出,不同预见期的洪峰和洪量相对误差均在±10 % 以内,除20200710号洪水在Δt=24和48 h的确定性系数较低外,其余2场洪水的确定性系数均较高,各预见期的确定性系数大于0.5。与表 2中校正后确定性预报结果比较,概率预报提供的中位数预报Q50在延长预见期的同时进一步保证了预报精度。在不确定性结果方面,3场洪水不同预见期的90 % 置信区间覆盖率均大于80 %,最高为97.56 %,最低为81.63 %;离散度均小于0.40,最低为0.03,最高为0.39;因此可见90 % 置信区间能够在较小的区间宽度内覆盖大部分的实测流量,可靠度较高。总体上,概率预报提供的Q50预报精度优于原确定性预报结果,提供的90 % 置信区间亦具有较高精度。以20200616号洪水为例,图 5给出不同预见期的洪水概率预报结果。
| 表 3 不同预见期的2020年汛期3场洪水概率预报精度统计结果 Tab. 3 Statistical results of probabilistic forecasting accuracy of three floods in 2020 flood season with different forecast periods |
|
图 5 猴子岩水库流域20200616号洪水概率预报过程线结果 Fig.5 Probabilistic forecasting hydrographs of flood #20200616 in Houziyan Reservoir Basin |
以大渡河猴子岩水库以上流域为研究区,分别采用新安江模型和动态系统响应曲线误差校正方法开展确定性洪水预报和实时洪水校正,利用HUP模型实现洪水概率预报;据此构建了一种集确定性洪水预报、实时校正和概率预报于一体的洪水预报框架,在猴子岩水库流域应用效果较好。主要结论为:
1) 新安江模型模拟得到25场洪水的洪峰、洪量相对误差均满足精度要求,率定期和验证期的确定性系数平均值分别为0.69和0.72,整体精度较高。采用动态系统响应曲线技术进行误差校正后,率定期和验证期的平均确定性系数分别提高到0.82和0.81;以预报降雨为输入得到的未来48 h滚动预报结果,经动态系统响应曲线技术校正后,在延长预见期的同时亦能保证预报精度。
2) 基于HUP的概率预报模型具有进一步校正作用,中位数Q50预报精度在一定程度上优于实时校正后的确定性预报结果;90 % 置信区间能以相对较窄的区间宽度覆盖大部分实测流量,具有较高的可靠度。
| [1] |
Liang ZM, Dai R, Li BQ. A review of hydrological uncertainty analysis based on Bayesian theory. Advances in Water Science, 2010, 21(2): 274-281. [梁忠民, 戴荣, 李彬权. 基于贝叶斯理论的水文不确定性分析研究进展. 水科学进展, 2010, 21(2): 274-281.] |
| [2] |
Liu ZJ, Guo SL, Xu XF et al. Bayesian probabilistic hydrological forecasting: Progress and prospects. Journal of Hydraulic Engineering, 2019, 50(12): 1467-1478. [刘章君, 郭生练, 许新发等. 贝叶斯概率水文预报研究进展与展望. 水利学报, 2019, 50(12): 1467-1478.] |
| [3] |
朱华. 水情自动测报系统. 北京: 水利电力出版社, 1993.
|
| [4] |
Kalman RE. A new approach to linear filtering and prediction problems. Journal of Basic Engineering, 1960, 82(1): 35-45. DOI:10.1115/1.3662552 |
| [5] |
Hino M. Runoff forecasts by linear predictive filter. Journal of the Hydraulics Division, 1970, 96(3): 681-702. DOI:10.1061/jyceaj.0002373 |
| [6] |
Zhu H. Matrix equation solving method of Muskingum method. Journal of China Hydrology, 1987, 7(4): 7-9. [朱华. 马斯京根法的矩阵方程求解法. 水文, 1987, 7(4): 7-9.] |
| [7] |
Gu LH, Lai XJ. A real-time alternating updating method based on ensemble Kalman filter. Advances in Science and Technology of Water Resources, 2017, 37(2): 73-77. [顾炉华, 赖锡军. 基于集合卡尔曼滤波的实时校正方法. 水利水电科技进展, 2017, 37(2): 73-77.] |
| [8] |
Si W, Bao WM, Qu SM. Runoff error correction in real-time flood forecasting based on dynamic system response curve. Advances in Water Science, 2013, 24(4): 497-503. [司伟, 包为民, 瞿思敏. 洪水预报产流误差的动态系统响应曲线修正方法. 水科学进展, 2013, 24(4): 497-503.] |
| [9] |
Si W, Bao WM, Qu SM et al. Real-time flood forecast updating method based on mean areal rainfall error correction. J Lake Sci, 2018, 30(2): 533-541. [司伟, 包为民, 瞿思敏等. 基于面平均雨量误差修正的实时洪水预报修正方法. 湖泊科学, 2018, 30(2): 533-541. DOI:10.18307/2018.0224] |
| [10] |
Bao WM, Gu YW, Si W et al. Application of rainfall dynamic system response curve method for streamflow and sediment simulation in loess region. J Lake Sci, 2020, 32(2): 528-538. [包为民, 顾雨薇, 司伟等. 降雨动态系统响应曲线修正方法在黄土区域水沙模拟中的应用. 湖泊科学, 2020, 32(2): 528-538. DOI:10.18307/2020.0221] |
| [11] |
Huang YX, Liang ZM, Singh VP et al. A coupled dynamic system inversion model for higher accuracy in flood forecasting. Water Resources Research, 2022, 58(2): e2021WR030531. DOI:10.1029/2021WR030531 |
| [12] |
Liang ZM, Huang YX, Singh VP et al. Multi-source error correction for flood forecasting based on dynamic system response curve method. Journal of Hydrology, 2021, 594: 125908. DOI:10.1016/j.jhydrol.2020.125908 |
| [13] |
Wen YH, Li ZJ, Sun MK et al. Influence of rainfall input on real-time flood forecasting accuracy and forecast period. J Lake Sci, 2019, 31(1): 39-51. [温娅惠, 李致家, 孙明坤等. 降雨输入对实时洪水预报精度与预见期的影响. 湖泊科学, 2019, 31(1): 39-51. DOI:10.18307/2019.0104] |
| [14] |
Zhang J, Zhong PA, Xu B et al. Research on multi-step epitaxy method for auto-regressive real-time correction of flood forecasting. Journal of China Hydrology, 2019, 39(6): 41-45, 6. [张娟, 钟平安, 徐斌等. 洪水预报自回归实时校正多步外延方法研究. 水文, 2019, 39(6): 41-45, 6.] |
| [15] |
Xu J, Li ZJ, Huo WB et al. Comparison of real-time correction methods of flood forecasting in semi-humid watershed. Journal of Hohai University: Natural Sciences, 2019, 47(4): 317-322. [徐杰, 李致家, 霍文博等. 半湿润流域洪水预报实时校正方法比较. 河海大学学报: 自然科学版, 2019, 47(4): 317-322.] |
| [16] |
Zhang L, Wang GL. Analysis on error distributions of input data and output data of flood forecasting model and its correlation. Journal of China Hydrology, 2022, 42(1): 23-28. [张琳, 王国利. 洪水预报模型输入与输出的误差分布及相关性分析. 水文, 2022, 42(1): 23-28.] |
| [17] |
Jiang XL, Gupta HV, Liang ZM et al. Toward improved probabilistic predictions for flood forecasts generated using deterministic models. Water Resources Research, 2019, 55(11): 9519-9543. DOI:10.1029/2019WR025477 |
| [18] |
Beven K, Binley A. The future of distributed models: Model calibration and uncertainty prediction. Hydrological Processes, 1992, 6(3): 279-298. DOI:10.1002/hyp.3360060305 |
| [19] |
Raftery AE, Gneiting T, Balabdaoui F et al. Using Bayesian model averaging to calibrate forecast ensembles. Monthly Weather Review, 2005, 133(5): 1155-1174. DOI:10.1175/mwr2906.1 |
| [20] |
Ajami NK, Duan QY, Sorooshian S. An integrated hydrologic Bayesian multimodel combination framework: Confronting input, parameter, and model structural uncertainty in hydrologic prediction. Water Resources Research, 2007, 43(1): W01403. DOI:10.1029/2005WR004745 |
| [21] |
Todini E. A model conditional processor to assess predictive uncertainty in flood forecasting. International Journal of River Basin Management, 2008, 6(2): 123-137. DOI:10.1080/15715124.2008.9635342 |
| [22] |
Liang ZM, Jiang XL, Qian MK et al. Probabilistic flood forecasting considering heterogeneity of error distributions. Journal of Hydroelectric Engineering, 2017, 36(4): 18-25. [梁忠民, 蒋晓蕾, 钱名开等. 考虑误差异分布的洪水概率预报方法研究. 水力发电学报, 2017, 36(4): 18-25.] |
| [23] |
赵人俊. 流域水文模拟: 新安江模型与陕北模型. 北京: 水利电力出版社, 1984.
|
| [24] |
Krzysztofowicz R. Bayesian theory of probabilistic forecasting via deterministic hydrologic model. Water Resources Research, 1999, 35(9): 2739-2750. DOI:10.1029/1999WR900099 |
| [25] |
Krzysztofowicz R, Maranzano CJ. Bayesian system for probabilistic stage transition forecasting. Journal of Hydrology, 2004, 299(1/2): 15-44. DOI:10.1016/j.jhydrol.2004.02.013 |
| [26] |
Jiang XL, Liang ZM, Hu YM et al. Research on assessment criteria in probabilistic flood forecasting. J Lake Sci, 2020, 32(2): 539-552. [蒋晓蕾, 梁忠民, 胡义明等. 洪水概率预报评价指标研究. 湖泊科学, 2020, 32(2): 539-552. DOI:10.18307/2020.0222] |
| [27] |
Darbandsari P, Coulibaly P. HUP-BMA: An integration of hydrologic uncertainty processor and Bayesian model averaging for streamflow forecasting. Water Resources Research, 2021, 57(10): e2020WR029433. DOI:10.1029/2020WR029433 |
| [28] |
Huang YX, Wang QZ, Liang ZM et al. Research advances on real-time correction methods for flood forecasting. South-to-North Water Transfers and Water Science & Technology, 2021, 19(1): 12-35. [黄一昕, 王钦钊, 梁忠民等. 洪水预报实时校正技术研究进展. 南水北调与水利科技(中英文), 2021, 19(1): 12-35.] |
 2023, Vol. 35
2023, Vol. 35 

