(2: 中国科学院南京地理与湖泊研究所, 南京 210018)
(3: 中国科学院大学南京学院, 南京 211135)
(4: 江西省鄱阳湖流域生态水利技术创新中心, 南昌 330029)
(2: Nanjing Institute of Geography & Limnology, Chinese Academy of Sciences, Nanjing 210018, P.R. China)
(3: University of Chinese Academy of Sciences, Nanjing, Nanjing 211135, P.R. China)
(4: Jiangxi Poyang Lake Basin Ecological and Water Conservancy Technology Innovation Center, Nanchang 330029, P.R. China)
洪水预报的目的是预测短、中、长期河道洪水的发生与变化趋势。它为防汛抢险和防洪系统调度等决策提供依据,为水资源的合理利用和保护、水利工程的建设和管理以及工农业的安全生产服务。我国降水时空分布不均匀,加之全球气候变暖导致的极端天气事件,使得我国近年来洪水灾害发生频繁,这种洪水灾害导致的巨额经济损失不容小觑,总而言之精准及时的洪水预报方案显得尤为重要。由于城市化的影响,流域中的下垫面情况较自然状态发生了巨大变化,这种变化使得以经验公式为基础的概念模型不得不重新考虑下垫面变化对经验公式的影响。其次,各种水利工程例如水坝等对自然的径流过程也有着较大影响,如Nilsson等[1]指出全球大部分的大型河流水文情势受到大坝建设的影响;而在我国已建库容在10万m3以上的水库工程98112座,其中大型水库744座,中型水库3938座[2],所以当前形势下考虑水利工程影响的洪水预报有着不言而喻的意义,精确的洪水预报可以为水库群之间防洪减灾和水资源调控提供实际支撑。
目前应用于洪水预报的水文模型主要有3种:(1)数学物理模型;(2)概念模型;(3)数据驱动模型(黑箱)[3-4]。随着计算机技术的发展,人工智能神经网络一家独大,而深度学习又逐渐成为人工智能机器学习领域的主流技术,将深度学习理论引入水文预报已经成为当下洪水预报新的发展方向[5-8]。长短期记忆模型(LSTM)相较于传统水文模型有着更强的非线性拟合和处理长期记忆的能力,在处理具有时序关系的问题上表现更加优秀[9-12],同时LSTM网络可以自动学习洪水和降雨的特征,具有更高的自适应性和普适性。但是LSTM模型的参数较多,率定参数工作量大且传统的率定方法主要依赖于经验或者人工的方法,容易导致模型的参数落入局部最优解以及泛化能力不强等问题[13],如何提高数据驱动模型在洪水预报中的准确性、可解释性,并增强对未来洪水预测的能力,是目前洪水预报领域的研究热点。针对这类问题本文采用优化算法代替人机交互率定。鲸鱼优化算法(whale optimization algorithms,WOA)有操作简单、参数少以及跳出局部最优解能力强等优点,在求解优化问题中展现出优良的性能和广泛的应用前景[14]。
因此,本文以浙江省横锦水库为研究对象并且选用新安江模型[15]为对比模型,基于1986—1997年洪水资料对该流域进行次洪模拟,引入优化算法和长短期记忆网络构建浙江横锦水库洪水预报模型,通过置换特征重要性(permutation feature importance)、SHAP(Shapley additive explanations)方法确定特征权重,再结合传统水文方法分析模拟结果的物理机制,以期提高神经网络模型的预报可解释性,为提高模型的外延性[16]提供一种新的思路。
1 数据与方法 1.1 研究区域及数据 1.1.1 研究区数据资料横锦水库(29°0′~29°20′N,120°00′~121°00′E)位于我国东南沿海,属于钱塘江水系,流域多山,土层较薄,并且水系发育良好。流域属典型的亚热带季风气候,受东亚季风影响,盛行东南风,降水有明显的季节变化,雨量丰沛但时空分布不均,空气湿润,雨热季节变化同步。横锦流域控制断面以上有两条支流汇入,控制站以上集水面积为378 km2,河长81 km[15]。选取该流域中7个雨量站(史姆、西坞、铜钱、窈村、龙坛、八达、横锦)1986—1997年的日蒸发量以及日降雨量和1 h时段降雨量。1个断面流量监测站(横锦站)的日流量和时段流量资料,时段长1 h,流域雨量站、流量站分布见图 1。本文以1986—1993作为模型的率定期,1994—1997年作为模型的检验期,具体率定期和检验期次洪资料的选择见图 2。

|
图 1 横锦水库地理位置及雨量站、流量站分布 Fig.1 The geographical location of Hengjin Reservoir and the distribution of rain stations and flow stations |

|
图 2 次洪资料率定期和检验期的划分 Fig.2 Division of regular and test period in sub-flood data rate |
研究中将水文站的上3个时刻时段流量值、6个雨量站和一个水文站的前3个时段和当前时段的雨量资料作为7个特征值输入模型作为输入数据,后第N时段的流量作为输出值,N为预见期,本文选预见期为1 h。
1.2 长短期记忆模型计算原理LSTM是一种对于传统的循环神经网络(recurrent neural network,RNN)的改进,在传统的RNN网络中信息由于梯度消失[17],无法学习到数据中的依赖关系。在LSTM模型中使用记忆细胞替换原先RNN中的细胞单元,从而能有效地提取出时间周期的序列数据特征值[18]。LSTM隐藏层中记忆细胞单元结构如图 3所示。

|
图 3 LSTM隐藏层中记忆细胞单元结构 Fig.3 The structure of memory cell unit in the hidden layer of LSTM |
LSTM区别于其他神经网络之处在于其拥有独特的单元状态(细胞状态),Ct表示神经网络对于t+1时刻前所有输入信息的总结。输入信息经过记忆细胞单元具体过程如下:
输入信息通过遗忘门,遗忘门决定了记忆细胞单元从上一状态中遗忘多少信息,其计算式为:
| ft=σ[Wf(ht−1,xt)+bf] | (1) |
式中,Wf为遗忘门的权重矩阵;bf为遗忘门的偏移向量;σ为sigmoid激活函数,ft经过sigmoid函数运算之后就被约束在(0,1),1表示“全部记忆”,0表示“全部遗忘”。
经过输入门,输入门决定哪些信息被记忆细胞单元添加到记忆中,其计算式为:
| it=σ[Wf(ht−1,xt)+bi] | (2) |
| ˜Ct=tanh[Wc(ht−1,xt)+bc] | (3) |
式中,Wf为输入门的权重矩阵,bi为输入门的偏移向量,
决定出遗忘和记忆的信息后,对记忆单元状态变量进行更新计算,其计算式为:
| Ct=ft⊙Ct−1+it⊙˜Ct | (4) |
式中,Ct为更新后的记忆单元状态变量,⊙是点乘运算。
处理后的数据最后通过输出门Ot,输出门的计算决定了隐藏层状态变量ht,其计算式为:
| Ot=σ[W0(ht−1,xt)+b0] | (5) |
| ht=Ot⊙tanh(Ct) | (6) |
式中,W0为输出门权重矩阵,b0为输出门偏移量。
1.3 鲸鱼优化算法及其改进WOA算法是受到自然界座头鲸捕食行为启发的一种智能优化算法,该算法较传统优化算法有精准度高且收敛速度快的特点。WOA算法的基本工作流程为:(Ⅰ)生成[0, 1]的随机数p,当p>0.5时采用泡泡网攻击方式,否则当|A|<1时进入猎物包围阶段,|A|≥1时进入搜索猎物阶段;(Ⅱ)随着迭代次数不断增加,a逐渐由2减小到0,|A|也逐渐收敛到0,算法从搜索猎物阶段过渡到包围猎物阶段[19]。但是由于WOA算法易陷入局部最优并且模型内参数调整方法简单从而使得全局探索和局部开发能力难以平衡[20]。本文使用基于混沌的正余弦策略来改进鲸鱼优化算法,具体改进步骤如下:(1)采用在WOA算法中寻优能力和收敛速度较好的Tent映射来生成初始种群[21];(2)使用正余弦算法(Sine cosine algorithm,SCA)作为全局优化算法筛选首领鲸鱼位置;(3)添加基于混沌理论的自适应权重,使算法的全局搜索和局部开发得到较好的平衡,一定程度上也增加了算法跳出局部最优区域的概率。该策略增加模型跳出局部最优的能力,减小了原有模型缺陷[21]。其改进的自适应权重计算式为:
| ω=ωs+(ωe−ωs)×lg(1+10tTmax) | (7) |
| X(t+1)=ω⋅X∗(t)−A⋅D | (8) |
| X(t+1)=ω⋅Xrand −A⋅Drand | (9) |
| X(t+1)=D′⋅ebl⋅cos(2πl)+ωX∗(t) | (10) |
式中,Tmax表示最大迭代次数;ωs表示惯性权重初始下限;ωe是最大迭代次数的惯性权重上限。研究表明,当ω在[0.4,0.9]之间变化时,算法具有较好的动态寻优能力。通常较大的惯性权重能够让算法具有较好的全局探索能力,而较小的惯性权重会使算法具有较好的局部开发能力,随着迭代的变化,将惯性权重从0.9非线性递减至0.4,表明模型实现以全局探索为主向局部探索能力为主的动态转变[22],本文所提改进的WOA算法的流程如图 4所示。

|
图 4 改进算法流程 Fig.4 The flow of the improved algorithm |
本文选择使用TensorFlow-GPU 2x深度学习框架来搭建网络结构,通过高阶应用程序接口Keras来进行深度学习模型的设计、调试、评估、应用。构建网络主要步骤为:
1) 数据预处理:本研究使用的是流量和降雨资料,由于数据的类型不同,数据差异较大,在输入模型之前需要将输入数据资料进行标准化。由于降雨和流量数据会时而出现异常值(极端事件),而异常值对极差标准化方法影响巨大,故使用标准差标准化公式(11)。对训练数据和测试数据分别进行标准化。
| x∗=x−ˉxσ | (11) |
式中,x为原始数据的均值;σ为原始数据的标准差;x为原始数据序列;x*为归一化后的新序列。
2) LSTM优化器选择:Bi-LSTM的激活函数选择ReLU,全连接层的激活函数为linear。并且优化器选择Adam算法。
3) 损失函数的选择:深度学习中可供选择的损失函数有多种,本次研究最终选择了较为常用的均方误差损失(mean squared error, MSE)[23],计算公式为:
| MSE=1nn∑i=1(y−yper)2 | (12) |
式中,y为实测值;yper为预测值;n为资料序列长度。
4) 数据校准计算:在输出结果通过马氏检验后,使用马尔科夫链对最后模型输出的数据进行残差校正。
1.4.2 模型参数选取本研究中模型的神经网络层数、学习率(learning-rate)、迭代轮次(epochs)、单次训练数据窗口大小(batch-size)、各层的节点数(units)由经验确定范围后由WOA优化算法迭代计算出。分别取Bi-LSTM为1、2、3、4层,在预见期为1 h时,分别独立模拟10次计算的纳什系数(NSE),模拟结果见图 5。本文选用模拟效果最好的3层Bi-LSTM构建LSTM模型。

|
图 5 不同Bi-LSTM层数模拟结果对比 Fig.5 Comparison of simulation results with different numbers of Bi-LSTM layers |
预报计算过程与实测过程之间的吻合程度可用确定性系数NSE来评定。NSE是一个标准化统计指标,其值介于(-∞, 1)之间,等于1表示模型结果完美拟合实测值。计算公式为:
| NSE=1−n∑i=1|yc(i)−y0(i)|2n∑i=1|y0(i)−¯y0|2 | (13) |
式中,y0(i)为实测值(m3/s);yc(i)为计算值(m3/s);y0为实测值的均值(m3/s);n为资料序列长度。
另外,还选择洪峰相对误差、径流深相对误差和峰现时差3个指标来评定预报精度。根据《水文情报预报规范》(GB/T 22482—2008)来最后评价预报方案精度。
1.5 神经网络解释方法本文采用在Python3.x中使用置换特征方法(permutation feature importance method,PFIM)和SHAP法来计算特征值的重要性,置换特征方法计算步骤为:(1)选择一个特征值,并且在数据集上对该特征值的所有数据进行随机排列。(2)计算新的模型预测结果。(3)对比新旧模拟结果的差异,差异越大说明该特征值越重要。
SHAP是一种用于解释机器学习模型预测结果的方法,它基于Shapley值的概念,给出了一种针对单个特征或特征组合的影响分析方法。在SHAP中,将每个特征视为博弈中的参与者,并将模型的预测视为博弈中的收益。通过使用多个样本来计算每个特征的Shapley值,SHAP提供了每个特征对模型预测的影响的全面解释。SHAP方法可以解释机器学习模型中每个特征的相对重要性,即在模型预测中每个特征对结果的贡献大小。
2 结果与讨论 2.1 预报精度总体效果评价 2.1.1 模型率定期参数设置及模拟结果文中的LSTM模型和WOA-LSTM模型的参数率定结果见表 1。LSTM的参数使用人机交互率定,而WOA-LSTM参数使用自动率定,选用NSE作为率定的适配度。为对比研究WOA-LSTM的模拟计算效果,对比模型选用在该地区运用较好的洪水预报模型——新安江模型[24],通过人机交互率定法得到新安江模型参数结果见表 2。
| 表 1 神经网络参数率定结果 Tab. 1 The results of parameter tuning for neural network |
| 表 2 新安江最终参数 Tab. 2 The final parameters of the Xin'an River |
图 6展示了率定期18场洪水的模拟结果,并采用NSE、均方根误差(RMSE)以及洪峰相对误差(绝对值)等指标评估了模型在率定期的性能表现。计算结果表明,在3个指标下,WOA-LSTM模型的性能表现均显著优于其他两个模型。具体而言,在率定期内,WOA-LSTM模型的RMSE值为7.23 m3/s,NSE值高达0.997,这表明该模型不仅能够准确地模拟洪峰流量,而且对洪水形状的刻画也非常精准。

|
图 6 率定期洪水模拟对比 Fig.6 Comparison of rate-constant flood simulation |
使用模型对检验期3年(1994—1997年)资料的7场洪水进行模拟计算。不同模型模拟计算结果见图 7,统计得到在检验期中LSTM、WOA-LSTM和XAJ 3个模型的NSE值分别为0.946、0.926和0.858,从NSE数值来看,神经网络模型能更好地表达出实测值和模拟流量之间的关系。图 7b显示了实测数据和模拟值的频率累积分布,4条线几乎一致表明3个模型都可以较好地模拟出该流域的洪水过程,但是由于模型本身和资料误差会导致模型在模拟过程中出现异常值。图 7a得出LSTM和WOA-LSTM在模拟过程中都出现了异常值,尽管LSTM模型能够更好地拟合小流量数据,在大流量模拟时表现欠佳。初步分析表明,这可能是由于模型结构复杂度和参数未达到最优配置,从而导致洪水预测偏大。为了进一步验证这一结论,表 3统计了检验期7次洪水事件的洪峰流量相对误差、NSE、径流深相对误差以及峰现时差。

|
图 7 检验期7场洪水模拟结果对比 Fig.7 The comparison of simulation results for seven flood events during the verification period |
| 表 3 目标函数计算 Tab. 3 Objective function |
根据《水文情报规范》(GB/T 22482—2008),3个模型模拟的7场洪水,WOA-LSTM和XAJ模拟结果洪峰相对误差、径流深相对误差和峰现时差全部小于误差许可,除LSTM模拟的31950426号洪水峰现时差大于误差许可3 h外,其余预测洪水全部达标。洪峰相对误差的绝对值全部小于误差许可20%,但是LSTM模型预测的7场洪水中有6场洪水的预报洪峰大于实测值,存在系统误差,相对误差最大值为17.58,接近误差许可,这与图 7a得到的结论相吻合,说明LSTM在预测大流量时确实存在过拟合问题。而本文所使用的WOA-LSTM模型中由于优化的参数选取和MC矫正流量残差,虽然小幅度增大了洪水过程线的波动而减小了NSE值,但是却极大地减小了LSTM自身模拟洪峰偏大的误差。从模拟效果来看,WOA-LSTM的NSE平均值为0.915、LSTM的NSE平均值为0.928,而洪峰流量误差绝对均值却由LSTM模拟的8%下降到4.9%,降幅约为40%,可见鲸鱼优化算法、长短期记忆算法和马尔科夫链结合使用在保证流量预测精度的同时,避免了预测大流量时存在的过拟合问题,提升了洪峰流量预测精度。综上所述,WOA-LSTM拥有更好的模拟效果。
2.2 典型洪水模拟分析当相同的模型应用于不同的洪水过程时,其表现往往取决于降雨情况的复杂性。多峰洪水相比于单峰洪水,其洪峰流量的大小、时间、洪水过程等方面都更为复杂,而大流量洪峰由于短时间内迅速形成,数据采集和传输过程中可能存在延迟或遗漏,两种情况都会导致预报的准确性下降,本节对比分析了3个模型对检验期这两种典型洪水的模拟结果,分别为多次降雨造成典型多峰洪水(31940609、31950426)和单次强降雨带来的典型单峰洪水(31970818)。
从3次典型洪水的流量过程线(图 8)可以看出,XAJ模型在模拟复杂降雨过程带来的多峰洪水时,往往误差较大,尤其体现在洪峰流量和退水过程。而LSTM和WOA-LSTM模型却能较好地模拟多峰洪水的复杂过程。而在大洪水预报中,由于历史大洪水资料少,长短期模型能学习到的特征也会变少,从而影响到预测精度,在本文中加入了马尔科夫链残差矫正步骤可以在一定程度上减少由于学习资料少而带来的精度下降问题。图 8显示,31970818号洪水在检验期中洪峰流量最大,LSTM的模拟结果无论是洪峰流量还是峰现时间都有较明显的偏差,而这一偏差在WOA-LSTM中则变得微乎其微,说明这种改进策略在横锦水库的洪水预报中是可行的。

|
图 8 典型洪水流量过程线 Fig.8 Typical flood flow process line |
本节分析了3种模型在不考虑未来降雨情况下的预报能力,具体方法是从预报时刻开始,不考虑未来降雨资料,仅利用现有的实测降雨资料和流量资料作为模型输入,每1 h驱动一次模型,对洪水过程进行逐时段预报分析。
表 4表明,3种模型在预见期增加后预报能力都有所下降,当预见期为4 h时,WOA-LSTM、LSTM和XAJ对率定期洪水的综合NSE分别为0.88、0.84和0.74,WOA-LSTM模型有5场NSE优于其他两个模型,平均洪峰相对误差XAJ模型较低,但是总体相差不大。当预见期为6 h时,WOA-LSTM和LSTM的率定期综合NSE分别为0.72和0.58,WOA-LSTM模型要远好于LSTM,对于其他3个指标二者相差不大。当预见期为8 h时,WOA-LSTM和LSTM的率定期综合NSE分别为0.55和0.34,峰现时差分别为3和5 h,平均洪峰相对误差分别为22.9%和27.0%,平均径流深相对误差为21%和22%。在这4个指标中,WOA-LSTM模型的表现都要优于LSTM模型。虽然随着预见期增加WOA-LSTM模型预报精度有所下降,但是下降幅度要小于LSTM。总而言之,WOA-LSTM模型在预见期2~8 h内模拟结果都要好于其他两个模型。
| 表 4 不同预见期预报结果比较 Tab. 4 Comparison of forecast results at different lead times |
从不同预见期预测结果分析中可以看出神经网络模型的优势在于,即使没有实时降雨资料输入,它仍能够有效地考虑未来降雨对系统的影响。通过利用过去的降雨数据,神经网络能够推断未来降雨的潜在模式和趋势,从而提供对系统响应和预测的有价值信息。因此,该模型不仅在实时数据可获得时表现出色,而且在没有实时降雨资料时仍能提供有意义的预测和决策支持。例如在预见期6 h时,XAJ模型模拟的31940820号洪水洪峰相对误差高达48.4%,而其他两个模型模拟的洪峰相对误差在6%以内,仍然可以较好地刻画出洪峰流量,说明较传统水文模型在长预见期且无未来降水资料输入时表现不佳,神经网络模型依旧可以预测到一定的洪水特征。但是当预见期增加时,数据关联性减小,可能会使得模型学到无用特征而产生过拟合现象,导致模型预报精度下降[25]。在预见期为8 h时,WOA-LSTM和LSTM产生的loss曲线见图 9。在LSTM模型中随着迭代轮次增加,测试集的损失逐渐增大,证明在关联度差的数据集中LSTM模型确实会存在过拟合现象,而这种现象在WOA-LSTM模型训练时却并没有这么明显。证明由于WOA优化算法,进一步优化了神经网络结构,提高了模型的稳定性,降低了过拟合的风险。尽管LSTM在纳什效率方面表现更好,但在其他方面却不如WOA-LSTM,WOA-LSTM在综合效果上更出色。
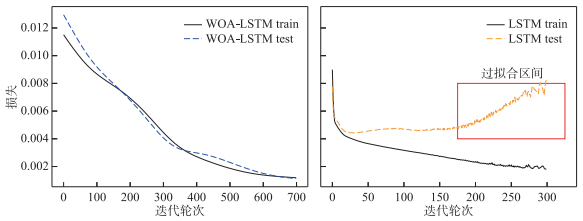
|
图 9 模型拟合损失曲线 Fig.9 The model fitting loss curve |
综上所述,WOA-LSTM在无需输入降雨资料的较长预见期内,可以一定程度上避免过拟合,从而保持良好的预测精度和鲁棒性。
2.4 WOA-LSTM可解释性的讨论神经网络模型是典型的黑箱子模型,由于本身不是构建于物理规律基础上的,所以模型可解释性较差,探究其参数和模型构造背后的物理意义逐渐成为神经网络模型新的发展方向[26]。
本文先使用PFIM法和SHAP法分别计算各特征值的重要性,再结合水文模型和气象学中使用较多的泰森多边形法(thiessen polygon method,TPM)和实际流域特性验证得到的雨量站面积权重的合理性。
由表 5泰森多边形计算结果表明横锦流域各雨量站重要性相似,结合图 1分析,说明研究流域中各雨量站分布均匀,面积权重应该相似。图 10对比了不同方法得到的特征值重要性值,除了SHAP法给横锦站赋予了较低的权重外,SHAP、泰森多边形、PFMI所计算的权重值分布大致相同,表明WOA-LSTM模型可以通过数据资料学习到流域中一定的雨量站面积权重特征,而这种面积权重是符合现实地理分布的。
| 表 5 不同方法的特征值权重 Tab. 5 Eigenvalue weights of different methods |

|
图 10 站点面积权重与特征值的重要性评估 Fig.10 Importance evaluation of the station area weight and characteristic value |
本文以横锦流域作为研究区域,结合改进的鲸鱼优化算法,马尔科夫链和长短期记忆神经网络共同构建洪水预报模型,讨论了在不同预见期下模型的预测性能、结合置换特征,SHAP方法增加了模型的可解释性,得到结果如下:
1) 在对场次洪水预报中,当预见期同为1 h时,检验期1994—1997年7场洪水的NSE值为0.926,径流深相对误差、洪峰相对误差和峰现时差全部在误差许可以内,且优于对比模型。
2) WOA-LSTM模型中WOA优化算法通过改变神经网络结构,从而降低模型在复杂数据集上的过拟合风险。
3) 通过泰森多边形,SHAP和置换特征值方法相互验证,表明WOA-LSTM模型可以在训练模型时学习到一定的物理机制,增加模型的可解释性。
综上所述,通过将优化算法和神经网络相结合,在一定程度上避免了人工率定超参数陷入局部解、过拟合等问题,并且在水库洪水预报过程中取得较好的成果,同时通过计算机方法和水文方法验证了神经网络在训练模型时可以学到一定的物理特征作为数据预测的基础,表明在以后的研究中可以结合置换特征值等一些新方法进一步增加神经网络的可解释性,增加模型计算结果的说服力。但是本文对于神经网络物理机制的研究还不够深入,今后可以通过更多的计算机方法,从神经细胞层面剖析模型的物理机制,增加模型的泛化能力,也可以结合水文统计等方法进一步提高模型预报结果精度。
| [1] |
Nilsson C, Renöfält BM. Linking flow regime and water quality in rivers: A challenge to adaptive catchment management. Ecology and Society, 2008, 13(2): art18. DOI:10.5751/es-02588-130218 |
| [2] |
中国科学院南京地理与湖泊研究所. 中国湖泊生态环境研究报告. 北京: 科学出版社, 2022.
|
| [3] |
Xu AL, Wang P. SWAT-based simulation of pollution from non-point agricultural sources. Environmental Monitoring and Forewarning, 2010, 2(1): 38-43. [徐爱兰, 王鹏. 基于SWAT模型的圩区农业非点源污染模拟. 环境监控与预警, 2010, 2(1): 38-43.] |
| [4] |
Hua SY, Gu SP, He J et al. Parameters optimization and application of three-water sources Xin'anjiang model. Water Resources and Power, 2013, 31(2): 23-26, 242. [华舒愉, 顾圣平, 贺军等. 三水源新安江模型参数优化及其应用. 水电能源科学, 2013, 31(2): 23-26, 242.] |
| [5] |
张宪超. 深度学习. 北京: 科学出版社, 2019.
|
| [6] |
Chang FJ, Chen PN, Lu YR et al. Real-time multi-step-ahead water level forecasting by recurrent neural networks for urban flood control. Journal of Hydrology, 2014, 517: 836-846. DOI:10.1016/j.jhydrol.2014.06.013 |
| [7] |
Bai Y, Chen ZQ, Xie JJ et al. Daily reservoir inflow forecasting using multiscale deep feature learning with hybrid models. Journal of Hydrology, 2016, 532: 193-206. DOI:10.1016/j.jhydrol.2015.11.011 |
| [8] |
Zhou YL, Guo SL, Zhang FZ et al. Hydrological forecasting using artificial intelligence techniques. Water Resources Research, 2019, 8(1): 1-12. [周研来, 郭生练, 张斐章等. 人工智能在水文预报中的应用研究. 水资源研究, 2019, 8(1): 1-12.] |
| [9] |
Yin FP, Jiang QY. Big data analysis method based on neural network. Software Guide, 2020, 19(9): 39-42. [殷芙萍, 江秋语. 基于神经网络的大数据分析方法. 软件导刊, 2020, 19(9): 39-42. DOI:10.11907/rjdk.201067] |
| [10] |
Kao IF, Zhou YL, Chang LC et al. Exploring a long short-term memory based encoder-decoder framework for multi-step-ahead flood forecasting. Journal of Hydrology, 2020, 583: 124631. DOI:10.1016/j.jhydrol.2020.124631 |
| [11] |
Huo WB, Zhu YL, Li ZJ et al. Comparison of Xin'anjiang model and Support Vector Machine model in the application of real-time flood forecasting. Journal of Hohai University: Natural Sciences, 2018, 46(4): 283-289. [霍文博, 朱跃龙, 李致家等. 新安江模型和支持向量机模型实时洪水预报应用比较. 河海大学学报: 自然科学版, 2018, 46(4): 283-289.] |
| [12] |
Yin ZK, Liao WH, Wang RJ et al. Rainfall-runoff modelling and forecasting based on long short-term memory (LSTM). South-to-North Water Transfers and Water Science & Technology, 2019, 17(6): 1-9, 27. [殷兆凯, 廖卫红, 王若佳等. 基于长短时记忆神经网络(LSTM)的降雨径流模拟及预报. 南水北调与水利科技, 2019, 17(6): 1-9, 27.] |
| [13] |
Zheng Z, Zhang HQ, Pan Y. Rolling bearing fault diagnosis based on IWOA-LSTM. Journal of Vibration and Shock, 2021, 40(7): 274-280. [郑直, 张华钦, 潘月. 基于改进鲸鱼算法优化LSTM的滚动轴承故障诊断. 振动与冲击, 2021, 40(7): 274-280.] |
| [14] |
Xu DG, Wang ZQ, Guo YX et al. Review of whale optimization algorithm. Application Research of Computers, 2023, 40(2): 328-336. [许德刚, 王再庆, 郭奕欣等. 鲸鱼优化算法研究综述. 计算机应用研究, 2023, 40(2): 328-336.] |
| [15] |
Shan CJ, Ji BH, Zhang QL. Research on flood forecast of Hengjin Reservoir based on Xinanjiang model. Journal of Zhejiang Water Conservancy and Hydropower College, 2021, 33(1): 28-31, 37. [山成菊, 纪碧华, 张群羚. 基于新安江模型的横锦水库入库洪水预报研究. 浙江水利水电学院学报, 2021, 33(1): 28-31, 37.] |
| [16] |
Hoedt P, Kratzert F, Klotz D et al. MC-LSTM: Mass-Conserving LSTM. International Conference on Machine Learning, 2021.
|
| [17] |
Zhao R, Yan RQ, Chen ZH et al. Deep learning and its applications to machine health monitoring. Mechanical Systems and Signal Processing, 2019, 115: 213-237. DOI:10.1016/j.ymssp.2018.05.050 |
| [18] |
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [19] |
Kingma DP, Ba JL. Adam: A method for stochastic optimization. San Diego: 3rd International Conference on Learning Representations, 2015.
|
| [20] |
Wang JH, Zhang L, Shi C et al. Whale optimization algorithm based on chaotic search strategy. Control and Decision, 2019, 34(9): 1893-1900. [王坚浩, 张亮, 史超等. 基于混沌搜索策略的鲸鱼优化算法. 控制与决策, 2019, 34(9): 1893-1900. DOI:10.13195/j.kzyjc.2018.0098] |
| [21] |
Sayed GI, Darwish A, Hassanien AE. A new chaotic whale optimization algorithm for features selection. Journal of Classification, 2018, 35(2): 300-344. DOI:10.1007/s00357-018-9261-2 |
| [22] |
Lin J, He Q, Wang Q et al. Chaos-based sine-cosine whale optimization algorithm. Intelligent Computer and Applications, 2020, 10(9): 43-48, 52. [林杰, 何庆, 王茜等. 基于混沌的正余弦鲸鱼优化算法. 智能计算机与应用, 2020, 10(9): 43-48, 52.] |
| [23] |
Chen ZR, Yin YJ, Wan B et al. Real-time Reservoir flood forecasting method based on LSTM network. Water Resources Research, 2021, 10(3): 312-321. [陈宗让, 殷延军, 万飚等. 基于LSTM网络的实时入库洪水预报方法. 水资源研究, 2021, 10(3): 312-321.] |
| [24] |
Zhao LP, Xing XG, Song J et al. Application of distributed Xin'anjiang model in flood forecasting of Hengjin Reservoir. China Flood & Drought Management, 2022, 32(7): 72-76. [赵丽平, 邢西刚, 宋君等. 分布式新安江模型在横锦水库洪水预报中的应用. 中国防汛抗旱, 2022, 32(7): 72-76.] |
| [25] |
Xu YH, Wu Q, Li CQ et al. Simulation of the flood process in the middle reaches of the Yellow River by a long-short term memory (LSTM) neuro network. Journal of Beijing Normal University: Natural Science, 2020, 56(3): 387-393. [徐源浩, 邬强, 李常青等. 基于长短时记忆(LSTM)神经网络的黄河中游洪水过程模拟及预报. 北京师范大学学报: 自然科学版, 2020, 56(3): 387-393. DOI:10.12202/j.0476-0301.2020156] |
| [26] |
Zhang W, Zheng YL, Liu ZW et al. Deep learning model guided by physical mechanism for reservoir operation. Journal of Hydroelectric Engineering, 2023, 42(3): 13-25. [张玮, 郑雅莲, 刘志武等. 物理机制引导的水库调度深度学习模型研究. 水力发电学报, 2023, 42(3): 13-25.] |
 2024, Vol. 36
2024, Vol. 36 


