(2: 长江水利委员会水文局长江三峡水文水资源勘测局, 宜昌 443000)
(3: 中国长江三峡集团有限公司, 宜昌 443100)
(2: The Three Gorges Hydrologic and Water Resources Survey Bureau, Bureau of Hydrology, Changjiang Water Resources Commission, Yichang 443000, P. R. China)
(3: China Three Gorges Corporation, Yichang 443100, P. R. China)
水面蒸发是湖泊和水库水量损失的重要途径,在全球范围内,水库的蒸发损失大于工业用水和生活用水的总消耗量[1]。三峡水利枢纽工程位于四川盆地与长江中下游平原结合部,控制长江上游流域面积约100万km2,占长江流域总面积的55.6%。三峡水库自蓄水以来,水体面积显著增加,175 m正常蓄水位下的水体面积高达1084 km2[2],水面蒸发损失在一定程度上影响了水库的水量平衡,进行水面蒸发的研究对三峡水库的水量平衡分析和三峡水利枢纽的科学调度具有重要意义。
比热容大和热传导速率低的特点以及流体特有的湍流扩散能力使得湖泊和水库的储热和放热潜力巨大,而大量储热的累积会导致水面蒸发相比净辐射具有季节相位的偏离,这就是蒸发滞后现象[3-5]。通常深水水体具有更大的储热能力,水储热的变化可能会达到净辐射的50% 以上[6],其蒸发与浅湖相比具有更长的滞后时间。Blanken等[7]发现,由于水储热的影响,五大湖中最深(平均深度148 m、最大深度406 m)且表面积最大的苏必利尔湖的最大蒸发量与最大净辐射之间存在5个月的滞后;Shao等[8]发现平均水深为19 m的伊利湖观测的地表能量通量呈明显的季节性变化,蒸发量与净辐射之间存在2个月的滞后;Lenters等[9]和Wang等[10]发现水深分别为10.9和1.9 m的Sparkling Lake和太湖的滞后时间均为1个月;Zhao等[11]发现平均水深为8.4 m的鄱阳湖滞后时间为22天。对于其他变量,Cui等[12]发现鄱阳湖的蒸发量与水汽压差、水面温度和气温在日内均存在明显顺时针的滞回曲线,与净辐射、风速和水气温差在日内均呈现逆时针循环。Zheng等[13]探讨了日尺度上蒸散发对气温、水汽压差和净辐射等环境变量的滞后响应,发现蒸发量与气温和水汽压差均有明显的滞后性,对净辐射的滞后响应不明显。对于滞后现象影响因素的分析大多在日内尺度进行[14-18]。
三峡水库属于河道型深水水库,自2003年6月开始蓄水,2010年10月达到正常蓄水位,水位每年在145~175 m之间呈周期性波动,水面面积和水深受水位变动的影响也具有显著周期性变化,正常蓄水位下三峡水库回水长度约660 km,其中约252 km的最大水深超过100 m。三峡水库的蓄水形成了较深的水深,导致库区产生了较大的热效应,水温产生了春夏季滞冷、秋冬季滞暖的年内滞后现象[19-20]。水温是衡量水体储热量的重要指标,水温的滞后反映了水体储热的变化,而水体储热和净辐射控制着水面蒸发时的可用能量,水体储热引起的可用能量的滞后就会导致水面蒸发的滞后(特别是深水水体)。2013年8月1日起三峡水文水资源勘测局在距三峡大坝约71 km的巴东河段设立了漂浮水面蒸发实验站(文中简称巴东站),并在附近岸上设有对应的陆面蒸发场进行对比观测,为定量分析水面蒸发年内滞后效应提供了基础。本文旨在根据研究期的数据,分析三峡巴东站蒸发量与影响变量间的年内滞后现象,为估算三峡水库水面蒸发提供基础。
1 数据来源与研究方法 1.1 数据来源巴东漂浮水面蒸发实验站(图 1)位于巴东县信陵镇(31°3′N, 110°22′E)。根据《水面蒸发观测规范》(SL 630—2013),在江面和岸边分别进行水面蒸发和相关气象要素的同步观测。巴东断面受水库调度影响,日最大水深在114.9~144.7 m之间波动,水面宽在647~784 m之间波动。陆上水面蒸发观测场高程181.3 m(1985国家高程基准),采用改进后的E601B型(水深约0.6 m)蒸发皿进行水面蒸发的观测,日蒸发量根据每日8:00的水深变化确定,并观测水面以下0.01 m水温,辅助气象站同步进行日照时数、地面以上1.5 m气温和湿度以及10 m风速的观测。水面蒸发场建在270 m2的等腰三角形水面钢结构浮筏上,依靠浮桶漂浮在水面,与陆面蒸发场的水平距离约为75 m,高程受三峡水库运行影响在143.3~173.3 m之间变化。蒸发器采用改进后的E601B型,外围圆形水圈的高度为80 cm,以防止水圈外的水体涌入蒸发器内,水圈底部保留直径为5 cm的圆孔以保证水圈内的水体与水库水体自由交换。气象要素的观测项目与陆面蒸发场相同,但风速观测高度为水面以上4 m。除水下0.01 m水温外,利用水面蒸发场同步观测长江水面以下0.5 m处水温。本研究收集了2013年8月1日-2020年7月31日的观测数据。研究中同时收集了巴东和寸滩水文站1992—2020年水位数据。

|
图 1 三峡水库巴东站水面与陆面蒸发场 Fig.1 Water and land surface evaporation sites of Badong Station in the Three Gorges Reservoir |
本文利用水面和陆面蒸发场观测的日照时数和水面温度估算净辐射[21]:
| Rn=Rns−Rnl | (1) |
| Rns=(1−α)Rs | (2) |
| Rs=(as+bsnN)Ra | (3) |
| Rnl=σTw4(0.34−0.14√ea)(1.35(as+bsnN)/(as+bs)−0.35) | (4) |
式中,Rn为净辐射,Rns和Rnl分别为净短波辐射和净长波辐射,MJ/(m2 ·d);Rs为太阳辐射,MJ/(m2 ·d),其中as、bs为经验系数,根据宜昌辐射站数据确定;n为实际日照时数;N为最大日照时数;α为水面反射率,通过郭生练等[22]发现的水面反射率与纬度的线性关系来计算每个月的水面反射率;Tw为水面温度,K;ea为实际水汽压,kPa。
1.2 时间滞后分析方法滞后模式通常通过双变量散点图形成的滞回曲线进行分析,以突出一个参数对另一个参数变化的响应。滞后关系可以从3个方面描述[12-13, 23-24]:(1)方向(顺时针或逆时针);(2)形状(线性、圆形或“8”字形);(3)滞回曲线所包围的面积。在建立滞回曲线时,需要用最大值对变量进行归一化处理(x/xmax,y/ymax),以消除不同单位对滞回曲线所包围面积大小的影响。逆时针即表明变量y相对于x具有时间上的滞后,“8”字形表示同时出现了顺时针和逆时针旋转,反应两个变量间在不同时期的相对滞后关系,而滞回曲线所包围面积越大表明时间上的滞后越长。
此外,通过错位移动法[8, 12, 25-26],即对变量的时段位移并分析相关关系的变化,根据最大确定性系数R2可以估算两个变量间的滞后时间。本研究在月时间尺度上进行,分析0~6个月逐月后移的R2变化,滞回曲线采用多年平均月数据进行分析。
2 结果分析 2.1 水面和陆面蒸发场蒸发量及相关气象要素的月变化研究期水面蒸发场E601B蒸发皿测得的蒸发量多年平均值为896.8 mm,在847.6~965.6 mm之间波动变化,陆面蒸发场E601B蒸发皿蒸发量的多年平均值为849.5 mm, 在778.1~925.8 mm之间波动变化。水面蒸发场测得的水面蒸发量年均值比陆面蒸发场高47.3 mm。
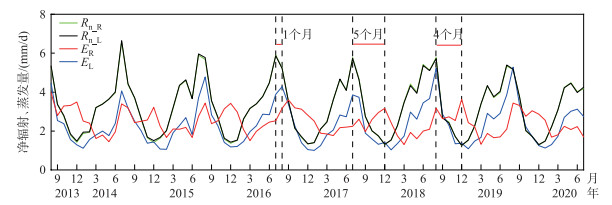
从2013年8月-2020年7月的时间序列(图 2)可以看出,水面蒸发场和陆面蒸发场根据日照时数计算得到的净辐射具有非常一致的变化(R2=0.99,P < 0.05),峰值一般都出现在7月,谷值出现在12月,但水面和陆面蒸发场的水面蒸发量变化差异显著。水面蒸发场蒸发量(ER)与陆面蒸发场蒸发量(EL)的R2仅为0.05,其中水面蒸发场蒸发量在年内具有明显的双峰变化,其第一个峰值与陆面蒸发场蒸发量的峰值出现在8月,而第二个峰值则出现在12月,对应的陆面蒸发场蒸发量在12月并无峰值。水面蒸发场蒸发量第二个峰值与陆面蒸发场蒸发量峰值存在1~5个月的滞后,平均滞后时间为3.7个月。水面蒸发场蒸发量两个峰值的日均蒸发量分别为2.61~3.60 mm/d(均值为3.28 mm/d)和3.04~3.63 mm/d(均值为3.33 mm/d),明显小于陆上水面蒸发量的峰值(3.86~5.28 mm/d,均值为4.58 mm/d)。水面蒸发场蒸发量与净辐射(Rn_R)无显著相关性(R2=0.01),第二个峰值相比于净辐射峰值存在显著滞后,滞后时间为2~5个月,平均4.1个月。陆面蒸发场蒸发量则与净辐射(Rn_L)具有相似的单峰变化(R2=0.81, P < 0.05),峰值相对于净辐射存在约1个月的滞后。
|
图 2 2013年8月-2020年7月巴东站水面和陆面蒸发场的净辐射(Rn_R、Rn_L)和蒸发量(ER、EL)的变化过程 Fig.2 Change process of net radiation (Rn_R and Rn_L) and evaporation (ER and EL) in the water and land surface evaporation sites of Badong Station from August 2013 to July 2020 |
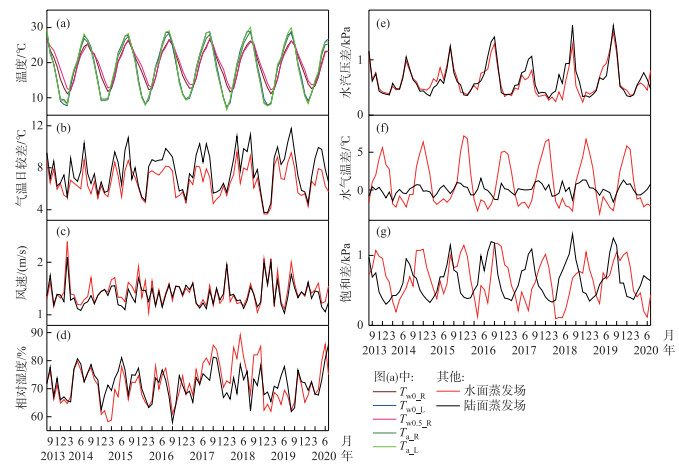
图 3a中,水面与陆面蒸发场的平均气温(Ta_R、Ta_L)具有相似的变化(R2接近于1),峰值出现在7、8月,谷值出现在1、2月。两种蒸发场的水面温度之间则存在显著差异(R2=0.83,P < 0.05),水面蒸发场水面温度(Tw0_R)的峰值均出现在8月(均值为26.3℃),谷值出现在2月(均值为11.9℃),而陆面蒸发场水面温度(Tw0_L)的变化与气温相似,其峰值有多个年份出现在7月(均值为28.4℃),谷值出现在1月(均值为8.4℃),水面蒸发场水面温度的峰值均低于陆面蒸发场,而谷值均高于陆面蒸发场。从二者水面温度的多年变化可以看出,水面蒸发场水面温度的变幅明显小于陆面蒸发场,水面蒸发场水面温度在3—8月(均值为20.4℃)小于同期陆面蒸发场水面温度(均值为22.6℃),在9月-次年2月则相反(均值分别为17.8和14.5℃),水面蒸发场水面温度的峰值和谷值相对陆面蒸发场水面温度存在约一个月的滞后。水面蒸发场水下0.5 m处的水温(Tw0.5_R)与水面蒸发场水面温度虽具有相似的年际变化,但从多年变化来看仍存在微小滞后现象,表现为在3—8月水下0.5 m水温(均值为20.3℃)略低于同期水面温度,9月-次年2月(均值为19.0℃)则高于同期水面温度。
|
图 3 2013年8月-2020年7月巴东站水面和陆面蒸发场月气象要素变化过程(Ta、Tw0、Tw0.5分别表示气温、水面温度和水下0.5 m处水温,后缀R和L分别表示水面和陆面蒸发场,下同) Fig.3 Monthly meteorological element change process of water surface and land surface evaporation sites at Badong Station from August 2013 to July 2020(Ta, Tw0 and Tw0.5 represent air temperature, water surface temperature and water temperature at 0.5 meters underwater, respectively. R and L represent the water surface and land surface evaporation sites, respectively (the same below)) |
两种蒸发场的气温日较差平均相差0.5℃,其中水面蒸发场的偏低(图 3b)。风速都转换为2 m高风速后,水面蒸发场的风速(均值为1.43 m/s)整体略高于陆面蒸发场(均值为1.39 m/s),且二者具有相似的变化(图 3c)。平均相对湿度(RH)和饱和水汽压差(VPD)同样具有相似的变化(图 3d、e)。
受水温差异的影响,水面蒸发场的水面与大气温差(ΔT=Tw0-Ta)(均值0.88℃)显著高于陆面蒸发场(均值0.05℃)。陆面蒸发场的水气温差在0℃上下波动,而水面蒸发场水气温差在3—8月小于0℃(均值为-1.72℃),低于同一时期陆面蒸发场的水气温差(均值为-0.18℃),而在9月-次年2月大于0℃(均值为3.48℃),远高于同一时期陆面蒸发场(均值为0.28℃),且历年的峰值都出现在12月(图 3f)。水面与大气饱和差(Δe=ew*-ea, ew*为由水面温度计算得到的水面饱和水汽压)之间同样存在显著差异(图 3g),陆面蒸发场的饱和差峰值大致出现在8月,谷值出现在1—2月,水面蒸发场的峰值出现在10—12月,谷值出现在4月,水面蒸发场饱和差的峰值滞后于陆面蒸发场2~5个月,平均3.6个月。
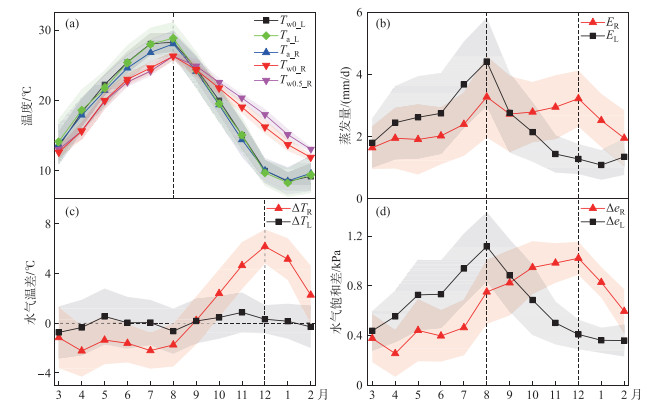
2.2 水面和陆面蒸发场水面蒸发季节变化的差异由水面和陆面蒸发场各温度的多年月平均图(图 4a)可以看出,水面蒸发场的平均气温(Ta_R)与陆面蒸发场的平均气温(Ta_L)和水面温度(Tw0_L)具有基本一致的年内变化,在3—8月均处于上升阶段,而9月-次年1月显著下降。水面蒸发场的水面温度(Tw0_R)和长江水下0.5 m处的水温(Tw0.5_R)则具有显著不同的季节变化,在3—8月低于陆面蒸发场的气温及水面温度,而在9月-次年2月则高于陆面蒸发场的气温和水温。
|
图 4 巴东站水面和陆面蒸发场气温和水温(a)、水面蒸发(b)、水气温差(c)、水面与大气饱和差(d)的年内变化(水平和垂直虚线表示0℃和曲线峰值在图中的位置) Fig.4 The annual variations of air temperature and water temperature (a), water surface evaporation (b), water-air temperature difference (c), water-air saturation difference (d)in the water surface and land surface evaporation sites of Badong Station(The horizontal and vertical dashed lines represent the positions of 0℃ and the peak values of the curves in the graph) |
水面蒸发场的水温和水下0.5 m水温在3—8月持续上升,而在9月-次年2月持续下降,故可将3—8月和9月—次年2月分别定义为水库水体的蓄能期和放能期。水面蒸发场气温在水体蓄能期间(均值为22.1℃)略低于陆面蒸发场气温(均值为22.8℃),而在水体放能期则无明显差异。水面蒸发场水面温度和水下0.5 m水温在水体蓄能期间(均值分别为20.4和20.3℃)明显低于陆面蒸发场水温(均值为22.6℃),且低于陆面气温(均值为22.8℃); 在放能期间(均值分别为17.8和19.0℃)则明显高于陆面水温(均值为14.5℃)和气温(均值为14.4℃)。水面蒸发场水面温度放能期与蓄能期均值的差值为-2.5℃,基绝对值远小于陆面蒸发场的-8.1℃(表 1)。
| 表 1 2013年8月-2020年7月水面和陆面蒸发场蒸发量和各气象要素在蓄、放能期的平均值 Tab. 1 The average values of evaporation and various meteorological elements in the water surface and land surface evaporation sites during the energy storage and release periods from August 2013 to July 2020 |
由图 4b~d也可以看出,两种蒸发场的蒸发量、水气温差和水气饱和差之间均存在显著差异。水面蒸发场蒸发量的峰值分别出现在8和12月,陆面蒸发场蒸发量的峰值只出现在8月,在放能期水面比陆面蒸发量多185.91 mm,在蓄能期则少138.68 mm; 水面蒸发场蒸发量在放能期与蓄能期均值的差值为84.78 mm,差距远小于陆面蒸发场的-239.81 mm。水面蒸发场的水气温差在蓄能期并无明显峰值,而在放能期的12月出现峰值,陆面蒸发场的水气温差ΔTL无明显峰值,在0℃附近波动变化。水面蒸发场水气温差在放能期与蓄能期的差值达到5.2℃,而陆面蒸发场仅为0.1℃。水面蒸发场的水面与大气饱和差同样呈双峰变化,峰值出现的时间与水面蒸发场蒸发量一致,其中12月的峰值更加明显,而陆面蒸发场的水气饱和差仅有一个峰值出现在8月。水面蒸发场水气饱和差放能期均值大于蓄能期均值,差值为0.42 kPa, 而陆面蒸发场水气饱和差则是放能期均值小于蓄能期均值,差值为-0.22 kPa。
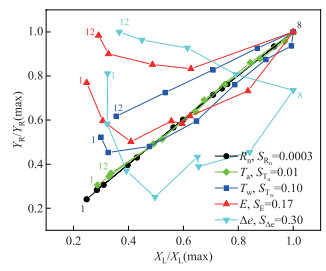
2.3 水面蒸发场相对陆面蒸发场的滞后效应通过建立水面与陆面蒸发场相同变量间的滞回曲线可以看到变量间的滞后关系(图 5)。水面蒸发场相对于陆面蒸发场的净辐射和气温的散点都近似分布在一条直线上,且滞回曲线包围的面积均在0.01以下,故不存在滞后。水面温度、蒸发量和水气饱和差滞回曲线的方向均为逆时针旋转,滞回曲线所包围的面积分别为0.10、0.17和0.30,表明水面蒸发场的变量均滞后于陆面蒸发场,滞后程度最大的为水气饱和差。从变量之间不同滞后月的确定性系数变化(表 2)也可以看出,两个蒸发场的净辐射和气温的R2在没有延迟的情况下达到最大,表明两种蒸发场的净辐射和气温并不存在滞后;两个蒸发场的水面温度、蒸发量和水气饱和差之间的滞后时间分别为1个月以内、3个月和4个月,水气饱和差之间的滞后时间最长。
|
图 5 水面与陆面蒸发场变量间的滞回曲线(图中数字代表月份) Fig.5 Hysteresis curve between variables of the water surface and land surface evaporation sites (the numbers in the figure represent month) |
| 表 2 巴东站水面蒸发场相对于陆面蒸发场变量之间不同滞后月的确定性系数 Tab. 2 Deterministic coefficients of different hysteresis months between the variables of the water surface and land surface evaporation sites of Badong Station |
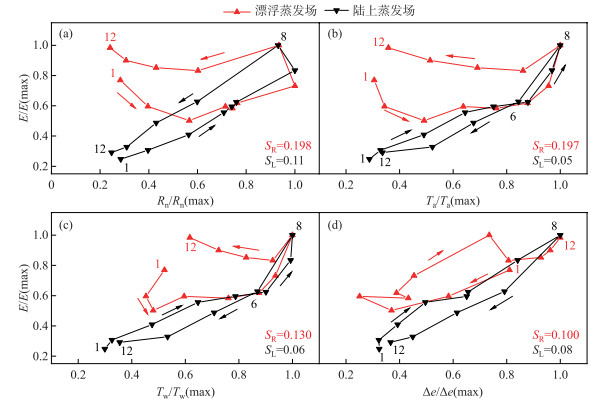
水面蒸发场的蒸发量与净辐射、气温和水面温度之间的滞回曲线具有明显的逆时针旋转(图 6),滞回曲线包围的面积分别为0.198、0.197、0.13,表明水面蒸发相对净辐射、气温和水面温度具有滞后现象。由表 3可以看出,水面蒸发场蒸发量与其净辐射、气温和水面温度分别在推迟对应变量4、3和2个月后R2达到最大,表明蒸发量相对于净辐射、气温和水面温度的滞后程度依次递减。水面蒸发场蒸发量与水气饱和差的滞回曲线为顺时针旋转,而二者的确定性系数也在没有延迟的情况下最大,表明水面蒸发场蒸发量相对水气饱和差并不存在滞后。
|
图 6 水面和陆面蒸发场水面蒸发相对不同变量的滞后现象(图中数字代表月份) Fig.6 The hysteresis phenomenon of water surface evaporation in water surface and land surface evaporation sites relative to different variables(the numbers in the figure represent month) |
| 表 3 水面与陆面蒸发场蒸发量与影响变量之间滞后月的确定性系数 Tab. 3 The coefficient of certainty for the hysteresis months between evaporation and influencing variables in the water surface and land surface evaporation sites |
陆面蒸发场蒸发量与净辐射为逆时针旋转,滞回曲线所围面积为0.11,表明陆面蒸发场蒸发量相对净辐射具有滞后现象。陆面蒸发量与气温、水面温度的滞回曲线均为“8”字形,陆面蒸发量在升温期间的3—5月大于降温期间10—12月,且此部分滞回曲线为顺时针,而升温期间6—7月的蒸发量小于降温期间8—9月的蒸发量,滞回曲线为逆时针,故陆面蒸发量与气温和水面温度的滞后出现在6—9月,但滞回曲线所围的总面积很小,仅为0.05和0.06,故滞后程度很微弱。陆面蒸发场蒸发量与水气饱和差的滞回曲线为顺时针,表明二者同样不存在滞后,且蒸发量在一定程度上先于水气饱和差。而陆面蒸发场蒸发量与这4个要素的确定性系数均在没有推迟的情况下最大,则表明滞后时间均在1个月以内或不存在滞后。陆面蒸发场的各滞回曲线的面积大小明显小于水面蒸发场,表明水面蒸发场蒸发量相对于影响变量的滞后程度明显强于陆面蒸发场蒸发量。
3 讨论湖泊(水库)水面蒸发的滞后时间与水深呈显著相关(表 4)。本研究中陆面蒸发场水深为0.6 m的E601B型蒸发器的滞后时间为1个月左右,与水深较浅的湖泊相近,如鄱阳湖(平均水深为8.4 m)、Sparking湖(10.9 m)、太湖(1.9 m)、洱海(10 m)以及Ross Rarnett水库(5 m)的滞后时间均在1个月左右。三峡水库巴东断面最大水深为114.9~144.7 m,本研究发现的水面蒸发滞后时间为4个月,与已有研究中较深湖泊蒸发的滞后时间一致。
| 表 4 不同深度湖泊蒸发滞后时间概况 Tab. 4 Overview of evaporation lag time of lakes at different depths |
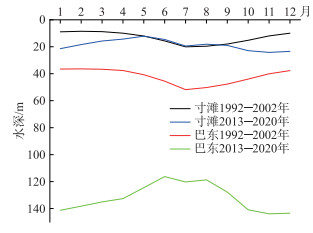
自然湖泊水深相对稳定,而三峡水库运行调度造成水深在年内具有显著周期性变化。时间上,三峡水库一般于9月开始蓄水,10月底之前完成蓄水; 11—12月,水库维持在高水位运行; 次年1—6月,水位逐步开始消落,6月10日之前消落至防洪限制水位(145 m水位)变动范围内。巴东断面汛期(6—8月)月平均最大水深在120 m左右,且全年最小水深出现在6月(约116.3 m),而在蓄水后的11—12月,水深均在140 m以上,全年的水位落差将近30 m(图 7)。水深在年内的变化对水储热具有显著影响,进而可能导致不同月的蒸发时间滞后效应产生差异,但本研究只分析了总体的时间滞后效应,下一步需要深入考虑水库运行调度影响下水深年内变化的影响。另一方面,三峡水库的蓄水会改变库区河段的水流情势,使库区河段水面变宽、过水面积增大、水流流速变缓,并最终使水体滞留时间变长,进而导致水体的储热在水平方向上传递和分布的效果变差,使水体储热累积,进而影响水面蒸发时的可用能量,导致更大程度的滞后效应。而在水库放水期,水流的流速相对较快,水体的储热在水平方向上会有更快的传递,水面蒸发滞后效应则可能会有一定程度的减弱。因此,下一步还需要分析水库蓄、放水过程中水体水平平流对水面蒸发时间滞后效应的影响。
|
图 7 三峡水库巴东和寸滩断面蓄水前(1997—2002年)和蓄水后(2013年8月-2020年7月)月平均最大水深变化 Fig.7 The monthly average maximum water depth changes of Badong and Cuntan sections of the Three Gorges Reservoir before (1997-2002) and after (from August 2013 to July 2020) impoundment |
此外,三峡水库库尾到库首沿程河段水深具有显著差异,在库尾距大坝605.7 km的寸滩断面年平均水深仅18.6 m,远小于巴东断面,不同断面的水储热以及水面蒸发的时间滞后效应也必然存在显著差异,在对整个三峡水库时间滞后效应的分析中需要考虑沿程水深变化的影响。
水温是估算三峡水库水面蒸发的关键。已有研究发现[19]三峡水库自2003年蓄水以来,库首的庙河断面在2006—2013年每年4—6月均出现了水温分层现象,但从2014年开始,水温垂向差异变小,水温不分层,且春季、秋季和冬季水温升高,下泄水温进一步平坦。也有研究发现三峡水库近坝区的水温分层现象会受上游溪洛渡、向家坝等梯级水库运行的影响而减弱[35],同时梯级水库还存在滞温现象,即降温期水库的下泄水温高于入库水温和天然河道水温,在升温期反之,这与杜林霞等[36]得出的三峡水库蓄水使下游宜昌河道水温出现增温和滞后现象的结论一致。本研究发现水温影响下的水面与大气的饱和差的季节变化是三峡水库水面蒸发滞后的主要影响因素,未来对三峡水库沿程水温的时空变化特征以及蒸发滞后效应需进行更加深入的研究。
4 结论本文通过巴东地区2013年8月1日-2020年7月31日水面蒸发场与陆面蒸发场测得的各气象数据分析了三峡水库巴东段的蒸发特征,通过错位移动法和滞回曲线的方法分析了水面与陆面蒸发场蒸发量以及蒸发与各气象要素的相对滞后时间和滞后特性。主要结论如下:
1) 水面蒸发场蒸发量在年内呈双峰变化,峰值分别出现在8和12月;陆面蒸发场蒸发量仅在8月出现单峰值。两种蒸发场蒸发量在8月的峰值与净辐射峰值出现的时间一致。
2) 水面蒸发场蒸发量与净辐射、气温和水面温度分别存在4、3、2个月的滞后,陆面蒸发场蒸发量相对应的滞后时间均在1个月以内;水面与陆面蒸发场的水面温度、蒸发量和水气饱和差之间的滞后时间分别1、3和4个月,气温和净辐射之间不存在滞后。
3) 三峡水库巴东段水面蒸发的年内滞后效应主要受到水温变化引起的水面与大气饱和差在季节上滞后的影响,而水温除了会受到水库沿程的气象要素影响外,还会受到水库的运行调度后水深的时空变化影响和上游梯级水库的影响。水温是精确估算三峡水库水面蒸发的关键变量,未来对三峡水库沿程水温的时空变化特征以及蒸发滞后效应需更加深入的研究。
| [1] |
Zhao G, Gao HL. Estimating reservoir evaporation losses for the United States: Fusing remote sensing and modeling approaches. Remote Sensing of Environment, 2019, 226: 109-124. DOI:10.1016/j.rse.2019.03.015 |
| [2] |
Wang YT, Lin TT. Estimation of evaporation from water surface of Three Gorges Reservoir. Express Water Resources & Hydropower Information, 2022, 43(12): 27-30, 48. [王玉涛, 林涛涛. 三峡水库水面蒸发量估算. 水利水电快报, 2022, 43(12): 27-30, 48.] |
| [3] |
强耀辉. 青藏高原湖泊储热变化对湖泊蒸发的影响[学位论文]. 北京: 中国科学院大学, 2021.
|
| [4] |
Cui YF, Liu YB. Advances in observation and calculation of lake evaporation. J Lake Sci, 2023, 35(5): 1501-1517. [崔逸凡, 刘元波. 湖泊蒸发观测与计算方法研究进展. 湖泊科学, 2023, 35(5): 1501-1517. DOI:10.18307/2023.0501] |
| [5] |
Liu YB, Qiu GY, Zhang HS et al. Shifting from homogeneous to heterogeneous surfaces in estimating terrestrial evapotranspiration: Review and perspectives. Science China Earth Sciences, 2022, 52(3): 381-399. [刘元波, 邱国玉, 张宏昇等. 陆域蒸散的测算理论方法: 回顾与展望. 中国科学: 地球科学, 2022, 52(3): 381-399.] |
| [6] |
Allen RG, Tasumi M. Evaporation from American Falls Reservoir in Idaho via a combination of bowen ratio and eddy covariance. In: Impacts of Global Climate Change, ASCE, 2014. DOI: 10.1061/40792(173)527.
|
| [7] |
Blanken PD, Spence C, Hedstrom N et al. Evaporation from Lake Superior: 1. Physical controls and processes. Journal of Great Lakes Research, 2011, 37(4): 707-716. DOI:10.1016/j.jglr.2011.08.009 |
| [8] |
Shao CL, Chen JQ, Chu HS et al. Intra-annual and interannual dynamics of evaporation over western Lake Erie. Earth and Space Science, 2020, 7(11). DOI:10.1029/2020ea001091 |
| [9] |
Lenters JD, Kratz TK, Bowser CJ. Effects of climate variability on lake evaporation: Results from a long-term energy budget study of Sparkling Lake, northern Wisconsin (USA). Journal of Hydrology, 2005, 308(1/4): 168-195. DOI:10.1016/j.jhydrol.2004.10.028 |
| [10] |
Wang W, Xiao W, Cao C et al. Temporal and spatial variations in radiation and energy balance across a large freshwater lake in China. Journal of Hydrology, 2014, 511: 811-824. DOI:10.1016/j.jhydrol.2014.02.012 |
| [11] |
Zhao XS, Liu YB. Variability of surface heat fluxes and its driving forces at different time scales over a large ephemeral lake in China. Journal of Geophysical Research: Atmospheres, 2018, 123(10): 4939-4957. DOI:10.1029/2017jd027437 |
| [12] |
Cui YF, Liu YB, Gan GJ et al. Hysteresis behavior of surface water fluxes in a hydrologic transition of an ephemeral lake. Journal of Geophysical Research: Atmospheres, 2020, 125(12). DOI:10.1029/2019jd032364 |
| [13] |
Zheng H, Wang QF, Zhu XJ et al. Hysteresis responses of evapotranspiration to meteorological factors at a diel timescale: Patterns and causes. PLoS One, 2014, 9(6): e98857. DOI:10.1371/journal.pone.0098857 |
| [14] |
Gallego-Elvira B, Baille A, Martín-Górriz B et al. Energy balance and evaporation loss of an agricultural reservoir in a semi-arid climate (south-eastern Spain). Hydrological Processes, 2010, 24(6): 758-766. DOI:10.1002/hyp.7520 |
| [15] |
Xu SQ, McVicar TR, Li LC et al. Globally assessing the hysteresis between sub-diurnal actual evaporation and vapor pressure deficit at the ecosystem scale: Patterns and mechanisms. Agricultural and Forest Meteorology, 2022, 323: 109085. DOI:10.1016/j.agrformet.2022.109085 |
| [16] |
Zhang QA, Katul GG, Oren R et al. The hysteresis response of soil CO2 concentration and soil respiration to soil temperature. Journal of Geophysical Research: Biogeosciences, 2015, 120(8): 1605-1618. DOI:10.1002/2015jg003047 |
| [17] |
Zhang QA, Manzoni S, Katul G et al. The hysteretic evapotranspiration—Vapor pressure deficit relation. Journal of Geophysical Research: Biogeosciences, 2014, 119(2): 125-140. DOI:10.1002/2013jg002484 |
| [18] |
Zhang RF, Xu XL, Liu MX et al. Comparing ET-VPD hysteresis in three agroforestry ecosystems in a subtropical humid Karst area. Agricultural Water Management, 2018, 208: 454-464. DOI:10.1016/j.agwat.2018.06.007 |
| [19] |
Ji DB, Cheng ZQ, Long LH et al. Characteristics of thermal stratification in head area of Three Gorges Reservoir and ecological effects in different operation periods. Water Resources Protection, 2022, 38(3): 34-42, 101. [纪道斌, 成再强, 龙良红等. 三峡水库不同运行期库首水温分层特性及生态效应. 水资源保护, 2022, 38(3): 34-42, 101.] |
| [20] |
Zhou JJ, Yang Q, Zhang M. Thermal-effect of the Upper Yangtze Reservoirs and countermeasures. J Lake Sci, 2019, 31(1): 1-17. [周建军, 杨倩, 张曼. 长江上游水库群的热环境效应与修复对策. 湖泊科学, 2019, 31(1): 1-17. DOI:10.18307/2019.0101] |
| [21] |
Allen RG, Pereira LS, Allen RG et al. FAO Irrigation and Drainage Paper, 1977.
|
| [22] |
Guo SL, Cheng ZF. Estimation of catchment evapotranspiration by climatic approach. Hydrology, 1994, 14(5): 16-22. [郭生练, 程肇芳. 流域蒸散发的气候学计算. 水文, 1994, 14(5): 16-22.] |
| [23] |
Zuecco G, Penna D, Borga M et al. A versatile index to characterize hysteresis between hydrological variables at the runoff event timescale. Hydrological Processes, 2016, 30(9): 1449-1466. DOI:10.1002/hyp.10681 |
| [24] |
张权. 华北冬小麦—夏玉米轮作农田碳平衡特征及控制因素研究[学位论文]. 北京: 清华大学, 2014.
|
| [25] |
Zhao P, Rao XQ, Ma L et al. The variations of sap flux density and whole-tree transpiration across individuals of Acacia mangium. Acta Ecologica Sinica, 2006, 26(12): 4050-4058. [赵平, 饶兴权, 马玲等. 马占相思(Acacia mangium)树干液流密度和整树蒸腾的个体差异. 生态学报, 2006, 26(12): 4050-4058. DOI:10.3321/j.issn:1000-0933.2006.12.018] |
| [26] |
Zhang RF, Xu XL, Liu MX et al. Hysteresis in sap flow and its controlling mechanisms for a deciduous broad-leaved tree species in a humid Karst region. Science China Earth Sciences, 2019, 62(11): 1744-1755. DOI:10.1007/s11430-018-9294-5 |
| [27] |
Nordbo A, Launiainen S, Mammarella I et al. Long-term energy flux measurements and energy balance over a small boreal lake using eddy covariance technique. Journal of Geophysical Research, 2011, 116(D2): D02119. DOI:10.1029/2010jd014542 |
| [28] |
Haginoya S, Fujii H, Sun JH et al. Features of air-lake interaction in heat and water exchanges over Erhai Lake. Journal of the Meteorological Society of Japan Ser Ⅱ, 2012, 90C: 55-73. DOI:10.2151/jmsj.2012-c04 |
| [29] |
Zhang Q, Liu H. Interannual variability in the surface energy budget and evaporation over a large southern inland water in the United States. Journal of Geophysical Research: Atmospheres, 2013, 118(10): 4290-4302. DOI:10.1002/jgrd.50435 |
| [30] |
Li XY, Ma YJ, Huang YM et al. Evaporation and surface energy budget over the largest high-altitude saline lake on the Qinghai-Tibet Plateau. Journal of Geophysical Research: Atmospheres, 2016, 121(18): 410-470, 485. DOI:10.1002/2016jd025027 |
| [31] |
Li ZG, Lyu SH, Ao YH et al. Long-term energy flux and radiation balance observations over Lake Ngoring, Tibetan Plateau. Atmospheric Research, 2015, 155: 13-25. DOI:10.1016/j.atmosres.2014.11.019 |
| [32] |
Momii K, Ito Y. Heat budget estimates for Lake Ikeda, Japan. Journal of Hydrology, 2008, 361(3/4): 362-370. DOI:10.1016/j.jhydrol.2008.08.004 |
| [33] |
Guo Y, Zhang Y, Ma N et al. Long-term changes in evaporation over Siling Co Lake on the Tibetan Plateau and its impact on recent rapid lake expansion. Atmospheric Research, 2019, 216: 141-150. DOI:10.1016/j.atmosres.2018.10.006 |
| [34] |
Haginoya S, Fujii H, Kuwagata T et al. Air-lake interaction features found in heat and water exchanges over Nam Co on the Tibetan Plateau. SOLA, 2009, 5: 172-175. DOI:10.2151/sola.2009-044 |
| [35] |
Ren S, Liu L, Zhang DJ et al. Research on water temperature distribution in Xiluodu-Xiangjiaba-Three Gorges cascade reservoirs. Yangtze River, 2018, 49(3): 32-35, 40. [任实, 刘亮, 张地继等. 溪洛渡-向家坝-三峡梯级水库水温分布特性. 人民长江, 2018, 49(3): 32-35, 40.] |
| [36] |
Du LX, Niu LH, Huang T. Variation characteristics and influence analysis of water temperature in Three Gorges Reservoir. Express Water Resources & Hydropower Information, 2017, 38(6): 58-63. [杜林霞, 牛兰花, 黄童. 三峡水库水温变化特性及影响分析. 水利水电快报, 2017, 38(6): 58-63.] |
 2024, Vol. 36
2024, Vol. 36 


