(2: 中国科学院南京地理与湖泊研究所,南京 210018)
(3: 中国科学院大学南京学院,南京 211135)
(4: 江西省鄱阳湖流域生态水利技术创新中心,南昌 330029)
(2: Nanjing Institute of Geography and Limnology, Chinese Academy of Sciences, Nanjing 210018, P.R.China)
(3: University of Chinese Academy of Sciences, Nanjing, Nanjing 211135, P.R.China)
(4: Jiangxi Poyang Lake Basin Ecological and Water Conservancy Technology Innovation Center, Jiangxi 330029, P.R.China)
随着全球工业和城市化的迅速增长,外源氮磷等污染负荷不断在湖泊水生态系统中蓄积,导致湖泊富营养化问题日益加剧[1-5]。总磷作为湖泊富营养化的主要因素之一,过量的总磷输入会引发藻类过度生长,破坏水体透明度,导致湖泊生态系统失衡。这不仅威胁水质和生物多样性,还影响人类健康和经济活动。因此,迫切需要针对氮磷等污染物建立可靠的预测和溯源系统,以采取相应措施来减轻和管理水污染。湖泊中总磷由于复杂的循环机制和非平稳性,对其精确的预测十分困难。开发可解释的总磷浓度预测框架并辨析影响污染物的路径和权重对于缓解湖泊富营养化、保护水生态和实现可持续发展具有重要意义。
数值模拟模型是预测和解析水体中总磷迁移转化的重要工具之一。目前广泛使用的水质模型如WSAP、EFDC和MIKE等,在湖泊总磷的迁移和负荷计算等方面具有良好表现。然而,在实际应用中,开发复杂水质模型通常需要充分的数据支持,并且耗费大量时间。此外,水质模型的预测精度在很大程度上受边界条件的影响(例如天气条件和负荷输入),而这些条件往往难以准确预测,使其在水质预测方面仍有一定的局限性[6]。近年来,神经网络模型作为一种快速发展的数据驱动模型,在水质领域得到广泛应用。长短期记忆模型(LSTM)作为一种特殊的循环神经网络(recurrent neural network,RNN),相比较传统的RNN可以较好的克服梯度爆炸等问题,更善于在时间序列数据中捕获长期依赖关系[7]。在自然科学研究中,LSTM已经被广泛应用于洪水预报、水沙预报等领域,并且多数情况下模拟效果好于其他经典机器学习方法,例如人工神经网络(artificial neural network,ANN)[8]。但是,由于湖泊总磷浓度的变化与多种因素都存在相关性,数据特征值多、噪声、缺失以及非线性关系复杂等特点,单一的LSTM模型模拟总磷变化往往是具有挑战性的。在改进方法中,时频分解方法可以减少数据的复杂性从而使模型更容易学到正确的特征[9-11],Liu等提出了灰色关联法和小波分析等对模型输入数据进行了分解优化,降低了模型的过拟合风险提高了预报精度[12]。然而,小波分解需要选择合适的母波函数来处理信号,选择适合目标数据集的母波函数是十分困难的。相比较小波分析,Seasonal and Trend decomposition using Loess(STL)拥有更强的处理非线性数据和缺失数据的能力,作为一种局部回归分析方法相比较其他方法由于采用了小区间拟合减小了数据信息泄露的风险[13-14],可以用于长期趋势序列预测和短期波动分析,使得它在不同领域和应用中具有广泛的适用性。
缺乏物理机制的黑箱性质是限制数据驱动模型在水环境应用中最大障碍之一。为提高模型结果的泛化能力和可解释性,构建高精度的可解释机器学习水质预报系统是十分必要的。Shapley additive explanations (SHAP)方法可以应用于解释各种机器学习模型,包括黑盒模型(如神经网络)和白盒模型(如线性回归)中分类问题和回归问题的预测结果。Sushanth等将SHAP方法嵌入LSTM模型中[15],较好地预测水库调节流域的河水流量并且对特征值贡献度做了较好的解释。大量研究都表明SHAP法可以解释LSTM并且能够衡量特征组合对于预测的影响,帮助识别特征之间的相互作用[16-18]。
骆马湖作为中国淮河流域重要的调蓄水库,是典型的过水性质湖泊。近年来,骆马湖中氮磷营养盐呈上升趋势[19],并且周边工农业和水产养殖业的排放将会进一步增加骆马湖富营养化风险[20]。研究表明,骆马湖总磷涉及外源河道污染入侵和内源底泥释放等多个来源,复杂的影响机制使得长预见期下的趋势预测和污染源归因十分具有挑战性。解析其水质断面总磷的影响路径和对总磷变化趋势的准确预测对缓解骆马湖富营养化危机有着重要的意义。为进一步解决总磷预报精度不高和神经网络模型黑箱性质不可解释的问题,提高数据模型在模拟水质问题严重且影响路径复杂的湖泊中的水质变量转化和迁移时的实用性,本文(1)分析了骆马湖主要水质断面的总磷时空变化特征;(2)分别使用更适合长期序列的LSTM层和处理短期记忆更强的GRU层[21],构建了可解释的预测框架(STL-LSTM-SHAP explainable framework,SLSEF);(3)通过对比传统神经网络,并且结合水动力水质耦合模型交叉验证了SLSEF框架的预测能力和对特征值重要性评估的可靠性。
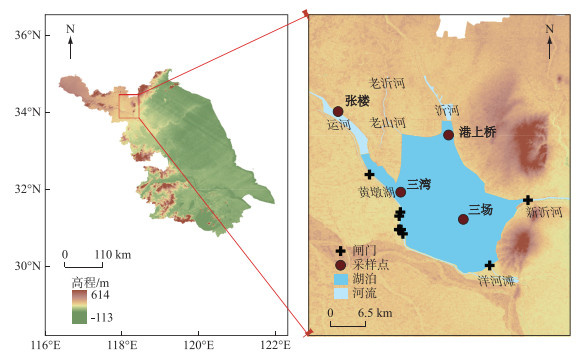
1 数据与方法 1.1 研究区域及数据 1.1.1 研究区数据资料骆马湖为江苏省四大湖泊之一,是淮河流域重要的蓄洪湖泊和行洪通道,又是南水北调东线工程的重要调蓄水库,骆马湖总面积375 km2,平均水深3.32 m。骆马湖属于暖温带半湿润季风气候,多年平均气温13.5℃,6 8月平均温度25.9℃,多年平均降水量910 mm,蒸发量904.7 mm。骆马湖湖水依赖地表径流和湖面降水补给,集水面积51215 km2, 补给系数197。入湖河流主要有沂河水系、运河等。骆马湖年水位变动为1.90~5.73 m,换水周期73 d,多年入湖水量介于0.8亿~78.3亿m3(2009-2020年),库容为9.2亿m3,是典型的受人工控制的过水性湖泊,地理位置见图 1。
|
图 1 骆马湖地理位置及采样点分布 Fig.1 Geographic locations of Lake Luoma and distribution of sampling points |
本文选用2021年1月20日-2022年3月14日的自动站检测7698 h的水质资料构建SLSEF,以数据中前80%作为率定期,后20%作为验证期。研究表明,骆马湖的总磷来源主要为外源含磷来水和自身内源磷释放两部分构成,其中内源磷与温度、pH和溶解氧呈显著相关[5, 22],所以本文使用前30 h的入湖口张楼断面和港上桥断面的水位和总磷浓度构成外源磷项,三湾断面的温度、pH和溶解氧作为骆马湖总磷的内源磷项,以及三湾断面历史总磷浓度组成混合框架的输入特征,1 h后的骆马湖(三湾)的总磷浓度作为混合框架的输出特征。
1.2 模型结构及评价体系 1.2.1 模型结构框架SLSEF框架主要结构主要包含预测和解释两部分组成。具体建模和评估步骤为: (1)使用线性插值法对原始序列的缺失值进行填补。再使用STL分解模型将处理后的数据分解为趋势项和变异项。(2)针对趋势项和变异项两个时间序列数据分别构建神经网络模型,对趋势项和变异项进行预测并且对2个模型的输入特征值进行重要性评估,结合SEM,分析特征之间的相互作用及对模型预测的影响和模型解释结果的准确性。(3)耦合2个模型的输出,评估模型最后的模拟结果。附图Ⅰ为建模-评估的主要步骤。
1.2.2 评价指标体系本文选取决定系数(R2)、均方根误差(RMSE)和平均相对误差(MRE)来评估不同算法的预测结果之间的准确性,具体计算公式分别为[23]:
| $ R M S E=\sqrt{\frac{1}{n-1} \sum\limits_{i=1}^n\left(x_i-y_i\right)^2} $ | (1) |
| $\operatorname{MRE}(\%)=\frac{1}{n} \sum\limits_{i=1}^n \frac{\left|y_i-x_i\right|}{y_i} \times 100 \% $ | (2) |
| $ R^2=1-\frac{\sum\limits_{i=1}^n\left|x_i-y_i\right|^2}{\sum\limits_{i=1}^n\left|y_i-\bar{y}_i\right|^2} $ | (3) |
式中,n为资料序列长度,xi为估计值,yi为测量值。
1.3 基于加权回归的季节趋势分解基于加权回归的季节趋势分解(seasonal-trend decomposition procedure based on loess,STL)利用局部加权回归(Loess)技术,通过对每一时间点的局部拟合减轻异常值的影响,提供了更稳健的时序分解结果。这一方法将时间序列细化为趋势、季节性和残差成分,适用于任何季节性频率超过1的数据[24]。计算式为:
| $ Y_t=T_t+S_t+R_t $ | (4) |
式中,Yt为t时刻的观测值,Tt、St、Rt分别为t时刻的趋势分量、周期分量、残差分量。
1.4 长短期记忆网络及变式长短期记忆模型(long-short-term-memory neural network,LSTM)是一种对于循环神经网络(recurrent neural network,RNN)的改进[25],其拥有独特的单元状态(细胞状态),Ct表示神经网络对于t+1时刻前所有输入信息的总结。输入信息经过记忆细胞单元具体过程如下:
1) 输入信息通过遗忘门,遗忘门决定了记忆细胞单元从上一状态中遗忘多少信息,遗忘门的计算式为:
| $ f_t=\sigma\left[W_f\left(h_{t-1}, x_t\right)+b_f\right] $ | (5) |
式中,Wf为遗忘门的权重矩阵;bf为遗忘门的偏移向量;σ为sigmoid激活函数,ft经过sigmoid函数运算之后就被约束在(0,1),1表示“全部记忆”,0表示“全部遗忘”。
2) 经过输入门,输入门决定哪些信息被记忆细胞单元添加到记忆中,其计算式为:
| $ i_t=\sigma\left[W_f\left(h_{t-1}, x_t\right)+b_i\right] $ | (6) |
| $ \widetilde{C}_t=\tan h \left[W_c\left(h_{t-1}, x_t\right)+b_c\right] $ | (7) |
式中,Wf为输入门的权重矩阵,bi为输入门的偏移向量,
3) 决定遗忘和记忆的信息后,对记忆单元状态变量进行更新计算,其计算式为:
| $ C_t=f_t \odot C_{t-1}+i_t \odot \widetilde{C}_t $ | (8) |
式中Ct为更新后的记忆单元状态变量,
4) 处理后的数据通过输出门Ot,输出门的计算决定了隐藏层状态变量ht,其计算式:
| $ O_t=\sigma\left[W_0\left(h_{t-1}, x_t\right)+b_0\right] $ | (9) |
| $ h_t=O_t \odot \tan h\left(C_t\right) $ | (10) |
式中,W0为输出门权重矩阵,b0为输出门偏移量。
门控循环单元(gated recurrent unit,GRU)作为一种对LSTM的简化,使用更新门和重置门代替了LSTM中的输入门、遗忘门、输出门,这使得GRU使用较少的训练参数,因此使用更少的内存并且比LSTM执行得更快,在单一的序列中GRU往往表现的更加出色[26]。
1.5 归因分析方法 1.5.1 SHAP分析法本文使用SHAP(SHapley Additive exPlanations)法来研究LSTM模型背后的预测逻辑,SHAP法是由Lundberg等[27]基于博弈论方法开发的。相比较传统变量重要性评估(皮尔逊相关)只能估计整体相关关系,SHAP法更适合于分析和解释神经网络模型潜藏的自然规律[28]。其中SHAP值可以根据公式(11)来计算,其计算式为:
| $ \phi_i=\sum\limits_{S \subseteq N}\left(\frac{|S|!(|N|-|S|-1)!}{|N|!}\right)\left[V\left(S \cup\left\{X_i\right\}\right)-V(S)\right] $ | (11) |
式中,
结构方程模型(structural equation model,SEM)是用于建立和评估多个变量之间的关系模型,可以同时考虑多个变量之间的综合关系并且其引入潜变量来更直观地表述变量之间潜在的影响机制和因果关系。同时,SEM还拥有完整的多重评估系统,多重评估指标可以帮助用户确保理论模型符合观察数据,提高模型测量的准确性和可靠性[30]。本文选用python中的semopy包作为平台搭建SEM,并且当模型指标满足以下条件约束时,模型被认为是有效的:比较拟合指数(CFI)>0.95,近似均方根误差(RMSEA)≤0.08,塔克·刘易斯指数(TLI)>0.95,拟合优度指标(GFI)>0.90[31-32]。
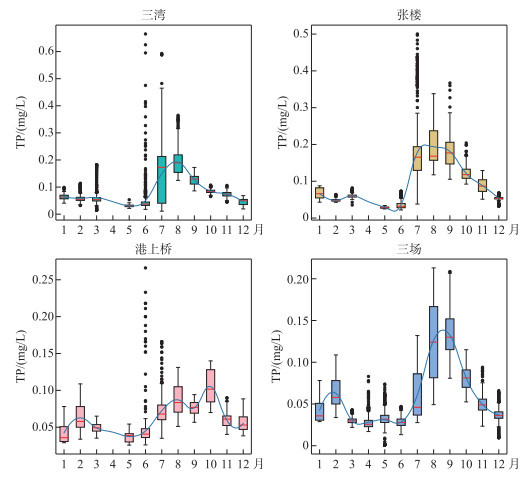
2 结果与分析 2.1 总磷时空异质性分析及数据处理 2.1.1 总磷时空异质性分析由图 2不同断面总磷时空分布来看,各断面总磷浓度变化范围不同,其中张楼断面年内平均总磷浓度(0.11 mg/L)明显高于港上桥断面(0.06 mg/L)、三场断面(0.06 mg/L)和三湾断面(0.08 mg/L)。三湾、三场和张楼断面的总磷浓度呈现明显的季节性差异,总体上各断面总磷浓度呈逐渐增高的趋势。受汛期影响,各段面总磷浓度都在8月份达到最高峰,在4月和5月份回到最低值,其中三湾和张楼断面总磷浓度峰值超过0.5 mg/L,汛期水质明显差于其他断面。
|
图 2 骆马湖主要水质断面总磷年内变化情况 Fig.2 Annual variation of total phosphorus at main water quality sections of Lake Luoma |
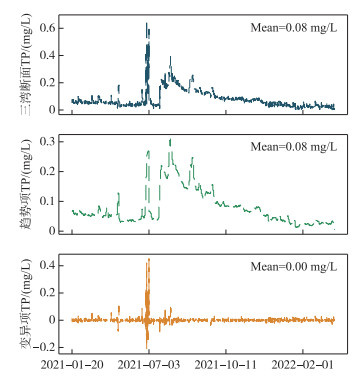
数据时间间隔为1 h,选取24 h作为平滑周期来分离趋势项和季节项,同时将季节项和残差项合并为变异项Vt。本研究中使用python中的statsmodels库来实现分解程序,时间序列资料分解结果见图 3。变异分量Vt符合正态分布且均值为0,证明STL方法可以在考虑日周期变化下,合理的将不同成分的分量从原始数据中分离。
|
图 3 三湾断面总磷的观测序列和分解成分 Fig.3 Observed sequence and decomposition components of total phosphorus in the Sanwan Section |
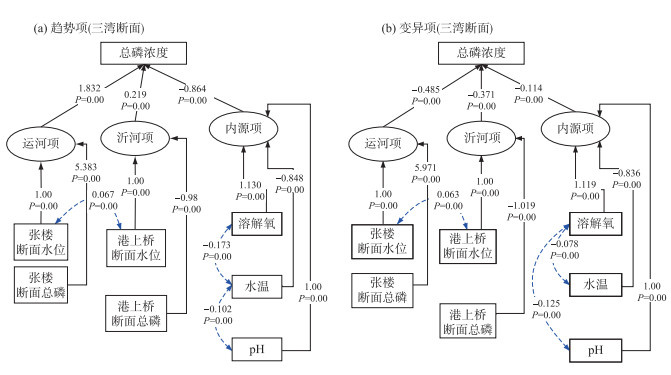
本节构建了SEM分析各个特征值的相关性,为了更好地解释测量变量对骆马湖(三湾)总磷的影响,本研究设计了3个潜变量:运河来源、沂河来源和内源项。图 4展示了SEM的结构和路径权重。表 1包含了对趋势项和变异项建立的SEM的评价指标。从表中可知,建立的模型可以较好地拟合样本数据。
|
图 4 SEM结构与路径权重图(P=0.00表示P<0.001) Fig.4 SEM structure and path weight diagram (P=0.00 indicates P < 0.001) |
| 表 1 SEM指标评价 Tab. 1 SEM index evaluation |
从绝对路径权重来看,无论是趋势项还是变异项,来源于运河的总磷都是影响骆马湖(三湾)总磷浓度的最大因素。从不同成分的权重变化来看,趋势项中内源性总磷项权重比例(29.6%)要明显高于变异项比例(11.8%)。从SEM统计结果来看,虽然运河是三湾断面总磷的主要污染来源,但是与变异项相比,趋势项总磷更容易受到温度、溶解氧等内源性因素的影响。
2.2 预报精度评估与比较本节探讨了LSTM、CNN-LSTM和STL-LSTM在骆马湖水质预报的适用性,在参数率定时,分别对3种不同的神经网络模型进行超参数率定,所有的实验都是在一台电脑上进行的,电脑CPU为intel i5-10500,GPU为英伟达gtx-1050ti,使用TensorFlow-GPU 2x深度学习框架来搭建网络结构,通过高阶应用程序接口Keras来进行深度学习模型的设计、调试、评估、应用,3个模型具体超参数见表 2。
| 表 2 模型参数设置 Tab. 2 Model parameter settings |
从评价指标表现来看,率定期SLSEF的3个评价指标都要好于其他2种网络结构,但是总体三者差别不大。而在验证期,CNN-LSTM的模拟能力下降明显,R2由0.979降至0.746,降幅为22%,而MRE则由7.088%上升到16.339%,涨幅为130.5%(表 3)。这可能是由于CNN-LSTM相较于其他网络虽然有更强的学习长期依赖关系的能力,但是水质数据非平稳性强、短周期内波动频繁,模型学习时可能产生过拟合现象,导致模型泛化能力不强。通过分解时间序列数据为趋势和变异2个成分,SLSEF能够对每个成分进行专门的建模,从而更好地捕捉和预测总磷的变化。这种分解和建模的方法使得SLSEF在解决长期趋势和周期性变化问题时具有较高的准确性和效果。在测试中,SLSEF表现出在率定期和验证期均优于其他模型,且在验证期仍能保持较好的预测精度。相比于验证期中LSTM和CNN-LSTM准确度分别下降了14%和22%,SLSEF下降了11%,这表明SLSEF泛化性更强,并且具有更好的预测能力和鲁棒性。
| 表 3 不同模型在率定期和验证期的预报表现 Tab. 3 The forecast performance of different models in the period of probability and validation |
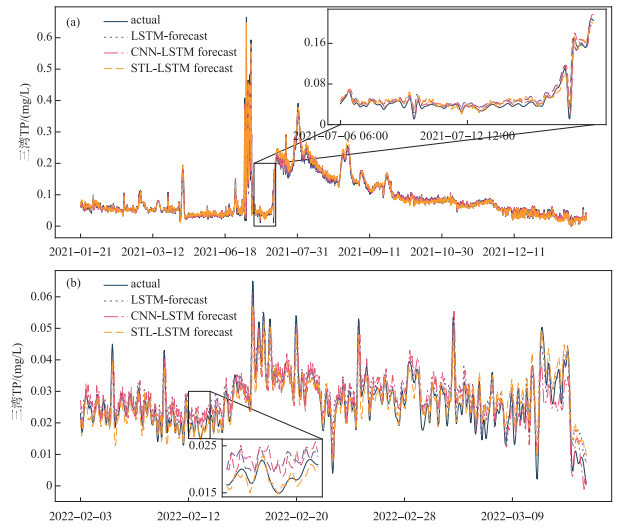
3种模型在率定期均表现出较好的预测能力,能够较为准确地模拟出三湾断面总磷的变化趋势和波动(图 5)。然而,在验证期内,CNN-LSTM模拟结果呈现出较多异常波动,这表明在模拟过程中确实存在过拟合现象。过拟合意味着神经网络学到了过多的细节和噪音,从而导致模拟结果的质量下降。相较之下,在验证期间,SLSEF更能准确地模拟总磷的趋势变化,且在波动较为复杂的时段没有出现过拟合现象。
|
图 5 不同模型在率定期(a)和验证期(b)下的表现 Fig.5 Performance of different models during calibration (a) and validation (b) periods |
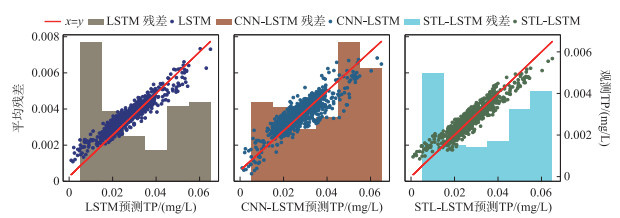
从总体分布来看,78.3%的总磷数据分布在[0.015, 0.035]范围内。图 5、图 6表明LSTM在模拟该区间总磷浓度时存在整体的偏移,LSTM和CNN-LSTM都存在模拟值偏大的系统误差。同时,由于极值学习数据较少,3个网络在模拟时都会存在残差变大现象。LSTM和CNN-LSTM在低值和峰值时的残差变化峰值分别为89.0% 和60.6%。相对而言,SLSEF的模拟结果中没有出现明显的系统偏差。同时,在极值模拟时,SLSEF的平均残差更小。这说明SLSEF在极值预测时仍能保持较高的预测精度,能够较准确地捕捉数据变化趋势和模式,有较强的稳定性,不受特定数据集的影响,能够更好地适应数据的长期变化和周期性波动特征,从而减小神经网络模型在水质数据预报中产生的系统偏差,验证期平均残差降低了20.0%。这种改进使得该框架在预测过程中能够提供更准确的结果,并更好地反映真实数据的特征。
|
图 6 验证期模型预测结果的散点图和残差分布 Fig.6 Scatterplot of model predictions and residual distribution during the validation period |
为探究不同模型在长预见期预报下对总磷的预报能力,分别建立了预报期为2~12 h的总磷预报框架。表 4展示了不同预见期下SLSEF、LSTM及CNN-LSTM在验证期下的预测表现。结果表明,在预见期为2 h时,3种模型的模拟结果R2分别降低了11.4%、32.9%和39.3%。LSTM和CNN-LSTM模型R2衰减速度明显快于SLSEF。当预见期大于2 h时,LSTM和CNN-LSTM的模拟结果R2均降至0.4以下,预测结果失去可靠性[33]。SLSEF在预见期为8 h时,仍能解释超过40%的数据信息,表明SLSEF在短期(预见期<3 h)和中长期(预见期<8 h)预测方面表现更为出色。
| 表 4 不同预见期下总磷模拟结果比较 Tab. 4 Comparison of total phosphorus simulation results in different forecast periods |
研究发现,当预见期大于2 h时,SLSEF中变异项R2会骤降至0.106。这表明,在湖泊总磷的中长期预报中,缺乏长期依赖信息的波动数据可能会导致单一神经网络(LSTM、CNN-LSTM)的模拟结果明显变差。SLSEF框架通过过滤无价值信息,更好地还原了总磷的变化趋势,可以为长预见期下的磷防治提供更有价值的决策依据。
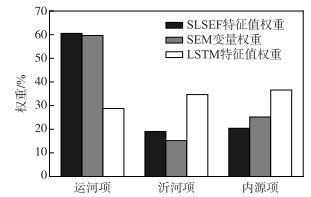
3 讨论 3.1 特征值相关性与差异分析特征权重反映了不同输入对模型预测结果的影响,权重越大表示其对结果的影响越显著。图 7为不同模型基于SHAP法计算的输入特征值权重,从数值上看,两者的权重分布存在较大差异。在SLSEF中,运河项占有最大比重(60%),而LSTM中的最大比重为内源项(37%)。值得注意的是,SEM得出的结论与SLSEF高度相似(R2=0.921)。SLSEF和SEM认为运河项是影响三湾断面总磷浓度的主要因素,说明LSTM可能未能正确学习特征值之间的相关关系。
|
图 7 不同模型特征值的权重分布 Fig.7 Weight distributions of feature values in different models |
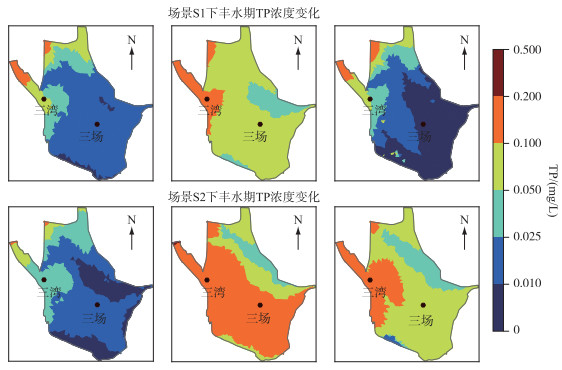
为进一步验证三湾断面的总磷来源组成以及模型结果的泛化能力,基于MIKE21[34]建立2种水动力场景:S1,其中主要来水源是沂河;S2,其中主要来水源是运河,用与研究不同来水条件下骆马湖流场的变化情况。图 8展示了不同场景下汛期总磷及流场的时空变化情况。通过这些额外的模拟结果,本研究可以更全面地评估SLSEF框架的性能和适用性。从全局来看,骆马湖总体水质和流场受上游来水影响严重,在S1场景下,当运河和沂河来水较少时,湖体内看不出明显的水流通道,总磷浓度分布在0.000~0.025 mg/L的水体占比78.1%。当沂河来水增加后,湖体呈现出明显的水流通道,水体大部分由沂河流入,从嶂山闸和洋河滩闸流出,在污染湖体同时,也会对湖体中心地区产生剧烈的扰动,搅动底泥导致内源磷的释放增加。尽管如此,从平均趋势来看,三湾断面不在过水通道上,仍然主要受到运河的控制。
|
图 8 汛期不同场景下TP和流场时空变化 Fig.8 Temporal and spatial variations of TP and flow field in different flood scenarios |
在S2场景下,当运河还未涨水时,流场和总磷分布与S1场景较为一致,水流稳定,没有明显的水流通道。然而,当运河来水增加时,出现明显过水通道。由于处在水流通道上,受到运河来水影响,三湾、三场断面总磷浓度超过0.100 mg/L,表明该断面水体都受到严重污染。
MIKE21水动力模型的研究结果表明,在S1和S2情景下,由于水动力条件的影响,三湾和张楼断面之间的物质传输和相互作用更为显著。这导致三湾断面的总磷浓度主要受到运河来水状况的调控,而在三场断面中,由于不同的来水状况,它受到2条河流交替影响。这一结论与SLSEF的研究结果一致。说明与LSTM相比,SLSEF所计算的权重更符合三湾断面的水动力条件,从而使得预测结果拥有更高的可信度和可解释性。
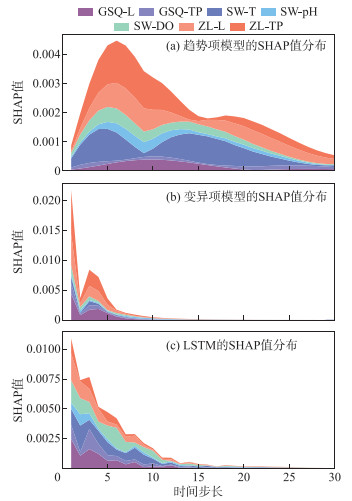
同时,研究发现基于SHAP计算的输入特征值的滞后相关度与水动力滞时可能存在显著相关性,会显著影响预测结果以及模型在不同预见期下的泛化能力[35],结合图 9可以看出,趋势项和变异项对输入的时间步长有不同的敏感性。对于骆马湖(三湾)断面的趋势项总磷而言,当时间步长为6~7 h时,其滞后相关性最大,其最大响应不会像变异项总磷那样在1 h(预见期)内立即出现。这说明污染物由张楼到三湾断面所需时间在6~7 h左右,而港上桥断面对三湾断面的物质运输时间则要更长。这导致趋势项中总磷的响应存在一定的滞后性,意味着影响因子对趋势项总磷的影响需要在较长的时间周期内才能被完全观察到。在20 h的时间步下,趋势项模型仍会赋予输入数据较高的权重值。对于变异项而言,当时间步长为1 h时,数据的SHAP值占全部的43.4%。然而,当时间步长6 h时,特征值权重降低至2.2%。这说明时间步长超过5 h,数据对于变异模型的输出结果将不再具有明显的影响。总体来说,SLSEF准确地识别了总磷中不同成分对时间步长敏感性的差异。其更透明的计算逻辑提供了更具说服力的解释,使得模型的结果更为可信。
|
图 9 向前30个时间步长下SHAP值的分布 Fig.9 Distribution of SHAP values at 30 time steps forward |
在同一分解项中,不同的成分对时间步长具有不同的敏感性。例如,在图 9a中,张楼断面的总磷和流量在6 h时具有最高的SHAP值(滞后相关性),而pH的SHAP峰值出现在9 h,这表明骆马湖(三湾)的趋势项总磷对内源磷的响应所需的时间更长。在相关研究中,发现pH通过调节吸附-解吸平衡来影响湖泊总磷,与外源磷相比,pH等影响因素的影响路径更为复杂[36]。因此,pH的响应时间较长,这进一步证实了由SHAP得出的结论的可靠性。这些发现有助于本研究更全面地理解骆马湖(三湾)中趋势项总磷和pH之间的动态关系。这表明SLSEF架构能够根据不同的分解项和成分赋予它们不同的权重值,从而提高了模型对数据的分析和解释能力。
图 9c中单一LSTM模型的SHAP值分布规律性不强,波动频繁,并且单一LSTM无法识别对时间步长敏感的成分,这些成分会造成模型在多步预测中丧失稳健性[35],这也可能是LSTM在长预见期下预报精度衰减快的原因之一。尽管LSTM成功模拟了总磷的变化趋势,却未能准确识别不同总磷成分之间的相关关系,导致预测结果的解释性较差,并在长期预测中表现出较快的精度衰减。相比之下,SLSEF架构通过综合考虑多个分解项和成分的贡献,在不同预见期下能够更准确地解释总磷变化,并提供更可靠的预测结果。
3.2 骆马湖总磷预测与归因研究结果表明基于LSTM开发的SLSEF模型比常见LSTM网络(LSTM、CNN-LSTM)在总磷预测的准确度和可解释性上都更有优势。湖泊总磷的变化受到外源和内源的共同作用,由于影响因素众多,这种变化常常被认为是非线性和不平稳的[5, 37-39]。随着计算机智能在生态领域发展,LSTM凭借着对序列依赖的自学习等特性,在很多研究中被证明可以用于总磷等水质要素的预报[40-41]。但是在实际应用中,研究发现骆马湖总磷复杂的变化给LSTM的预测带来了不小的困难,预测结果在验证集上的准确率下降了14%,这说明LSTM预测结果的泛化性是值得质疑的。在现有研究中,分解复杂数据可能成为提升LSTM网络学习能力的有效策略[42]。在实际应用中,相比较原始的LSTM,STL分解技术大大加强了LSTM网络的学习能力,在测试集上错误率减小了29%。STL技术还提高了LSTM网络的可解释性。简单的LSTM输入权重在时间维度上波动明显,各权重之间的大小关系也不符合骆马湖的水动力条件,而SLSEF架构下的归因结果与传统归因方法SEM以及水动力模型模拟结果高度一致。同时,研究还发现学习到正确权重特征的SLSEF在长预见期下的总磷预报中表现也优于LSTM,这说明STL技术可以明显提高LSTM的学习能力,使计算结果更有说服力。
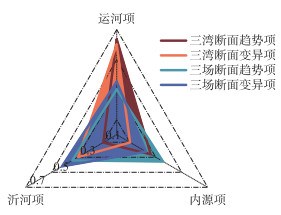
鉴于三湾断面与三场断面存在显著的水动力条件差异,为验证SLSEF在不同水动力条件下的适用性,本文选择将SLSEF框架应用于三场断面,以便全面地了解SLSEF在不同环境中的性能表现。经过MIKE21验证表明,SLSEF不仅能够预测三场断面总磷的变化趋势(R2=0.884),同时能够针对各个不同的断面情况计算出正确的特征值权重。根据图 10可知,不同断面间总磷的特征值影响权重存在较大差异。在三湾断面上,运河来水状况是影响总磷浓度的绝对因素,其占比为60.0%。然而,在三场断面中,运河和沂河的影响权重相对均衡,分别占总磷来源的32.7%和38.2%。这表明三场断面位于2条入湖河流的过水通道上,相较于三湾,受运河来水的影响较小。同时在非汛期,由于下游水流流速变慢,水体滞留时间更长使得温度等因素更容易加快湖体中磷化合物的分解,导致内源磷在三场断面的变异项中的比重明显增加。外源磷和内源磷的空间动态差异体现出骆马湖的水文复杂性,这一关系的明确对类似过水湖泊的污染物治理有一定的指导意义。
|
图 10 三湾和三场断面的总磷来源权重差异对比 Fig.10 Contrasting the weight differences of total phosphorus sources between Sanwan and Sanchang Sections |
研究表明,通过合理的闸坝调度,可以迅速将上游来水引导流出湖体,从而有效减轻湖体所承受的冲击,进一步降低骆马湖总磷的波动脉冲。长久来看,控制进入湖体的污染物总量以及改善流入湖区的河流水质,是改善骆马湖北部受汛期影响较小湖区和整体水质的根本策略。值得注意的是,由于湖泊和河道的水质标准存在差异,河道的水质常常较湖泊差。因此,严格管理湖区上游工农业废水排放显得尤为重要,这可以在很大程度上减轻骆马湖水体富营养化问题。综合而言,SLSEF框架的分析结果为骆马湖的水质管理提供了更为深刻的结果,也为相应的环境保护策略的制定提供了科学依据。
4 结论在本文中,基于LSTM网络开发了一种可解释的神经网络框架(SLSEF)。该方法拥有: a)更准确的预测结果,比LSTM及其常用的改进方法(CNN-LSTM)在总磷预测上表现更好; b)与LSTM相比,更强大的多步超前预测能力,在1~8 h内可以准确且稳定地预测总磷变化趋势; c)更可靠的解释结果,通过分解-预测-解释的方法,使得原本具有一定黑箱特性的神经网络模型获得了更高的透明度和预测准确性。这种方法不仅使用户能够深入理解模型对数据的处理方式,还能够将预测结果的依赖权重明确呈现。这样的解释性结果不仅可以用于科学研究,还可以为生态政策的制定提供有价值的决策依据,从而更好地保护和管理水体的生态环境。目前研究还存在一些不足,例如,训练数据的时间序列不够长,以及在分解预测框架结构中可能涉及的信息泄露等问题。由于骆马湖位于南水北调工程的路线上,调水可能在非汛期引发额外的水质波动,这种波动有可能对模型的拟合效果产生负面影响。在考虑水利工程的影响下,提升水质模型的预测精度成为当前亟需解决的热点问题。未来的研究将聚焦于运用更为高效的时频分析技术,结合深度学习模型,并通过与水动力学模型的综合交叉,实现在不同水利调度方案下更为准确的预测,进一步挖掘分解预测框架在工程应用前景和解释性方面的潜力。
5 附录附图Ⅰ见电子版(DOI: 10.18307/2024.0415)。
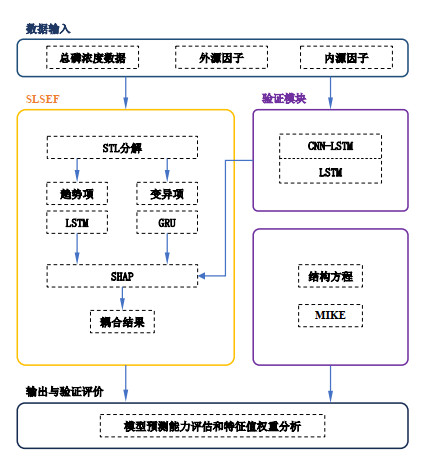
|
附图Ⅰ SLSEF模型建立与评估过程 AttachedFigA1 Establishment and evaluation process of the SLSEF Model |
| [1] |
Bao BL, Cui HB, Li HT et al. Phosphorus release characterization of biochar loaded with inherent and exogenous phosphorus and impact on soil Pb immobilization. Journal of Cleaner Production, 2023, 400: 136713. DOI:10.1016/j.jclepro.2023.136713 |
| [2] |
Dupas R, Delmas M, Dorioz JM et al. Assessing the impact of agricultural pressures on N and P loads and eutrophication risk. Ecological Indicators, 2015, 48: 396-407. DOI:10.1016/j.ecolind.2014.08.007 |
| [3] |
Lin SS, Shen SL, Zhou AN et al. Assessment and management of lake eutrophication: A case study in Lake Erhai, China. Science of the Total Environment, 2021, 751: 141618. DOI:10.1016/j.scitotenv.2020.141618 |
| [4] |
Soro MP, N'Goran KM, Ouattara AA et al. Nitrogen and phosphorus spatio-temporal distribution and fluxes intensifying eutrophication in three tropical rivers of Côte d'Ivoire (West Africa). Marine Pollution Bulletin, 2023, 186: 114391. DOI:10.1016/j.marpolbul.2022.114391 |
| [5] |
Yuan HZ, Chen PY, Liu EF et al. Terrestrial sources regulate the endogenous phosphorus load in Taihu Lake, China after exogenous controls: Evidence from a representative lake watershed. Journal of Environmental Management, 2023, 340: 118016. DOI:10.1016/j.jenvman.2023.118016 |
| [6] |
Liang ZY, Zou R, Chen X et al. Simulate the forecast capacity of a complicated water quality model using the long short-term memory approach. Journal of Hydrology, 2020, 581: 124432. DOI:10.1016/j.jhydrol.2019.124432 |
| [7] |
Nourani V, Behfar N. Multi-station runoff-sediment modeling using seasonal LSTM models. Journal of Hydrology, 2021, 601: 126672. DOI:10.1016/j.jhydrol.2021.126672 |
| [8] |
Zhang D, Lin JQ, Peng QD et al. Modeling and simulating of reservoir operation using the artificial neural network, support vector regression, deep learning algorithm. Journal of Hydrology, 2018, 565: 720-736. DOI:10.1016/j.jhydrol.2018.08.050 |
| [9] |
Cao M, Yang CY. Research on CNN-LSTM-Attention gas prediction model based on wavelet. Journal of Safety Science and Technology, 2023, 19(9): 69-75. [曹梅, 杨超宇. 基于小波的CNN-LSTM-Attention瓦斯预测模型研究. 中国安全生产科学技术, 2023, 19(9): 69-75.] |
| [10] |
Deng LJ, Yuan JB, Liu J et al. Detection method of wind speed anomaly fluctuation based on SSA-LSTM. Coal Science and Technology, 2023, 4(63): 1-9. [邓立军, 袁金波, 刘剑等. 基于SSA-LSTM的风速异常波动检测方法. 煤炭科学技术, 2023, 4(63): 1-9.] |
| [11] |
Xu ZX, Mo L, Zhou JZ et al. Stepwise decomposition-integration-prediction framework for runoff forecasting considering boundary correction. Science of the Total Environment, 2022, 851: 158342. DOI:10.1016/j.scitotenv.2022.158342 |
| [12] |
Liu MY, He JY, Huang YZ et al. Algal bloom forecasting with time-frequency analysis: A hybrid deep learning approach. Water Research, 2022, 219: 118591. DOI:10.1016/j.watres.2022.118591 |
| [13] |
He HT, Gao SC, Jin T et al. A seasonal-trend decomposition-based dendritic neuron model for financial time series prediction. Applied Soft Computing, 2021, 108: 107488. DOI:10.1016/j.asoc.2021.107488 |
| [14] |
Guo LJ, Xu RW. Application of LSTM Model Combining Improved Fruit-Fly Algorithmafter Seasonal-Trend Decomposition using LOESS towater quality prediction. Journal of Yangtze River Scientific Research Institute, 2023, 40(8): 57-63. [郭利进, 许瑞伟. 基于改进果蝇算法的LSTM在水质预测中的应用. 长江科学院院报, 2023, 40(8): 57-63.] |
| [15] |
Sushanth K, Mishra A, Mukhopadhyay P et al. Real-time streamflow forecasting in a reservoir-regulated river basin using explainable machine learning and conceptual reservoir module. Science of the Total Environment, 2023, 861: 160680. DOI:10.1016/j.scitotenv.2022.160680 |
| [16] |
Baptista ML, Goebel K, Henriques EMP. Relation between prognostics predictor evaluation metrics and local interpretability SHAP values. Artificial Intelligence, 2022, 306: 103667. DOI:10.1016/j.artint.2022.103667 |
| [17] |
Chehreh Chelgani S, Nasiri H, Alidokht M. Interpretable modeling of metallurgical responses for an industrial coal column flotation circuit by XGBoost and SHAP-A "conscious-lab" development. International Journal of Mining Science and Technology, 2021, 31(6): 1135-1144. DOI:10.1016/j.ijmst.2021.10.006 |
| [18] |
Deb C, Dai ZH, Schlueter A. A machine learning-based framework for cost-optimal building retrofit. Applied Energy, 2021, 294: 116990. DOI:10.1016/j.apenergy.2021.116990 |
| [19] |
Hu KY, Wang JD, Lan L et al. Analysis of abnormal water quality change and potential ecological risk in Luoma Lake, Jiangsu Province. Acta Scientiae Circumstantiae, 2022, 42(6): 197-205. [胡恺源, 王金东, 兰林等. 骆马湖水质变化异常及潜在生态风险分析. 环境科学学报, 2022, 42(6): 197-205. DOI:10.13671/j.hjkxxb.2021.0414] |
| [20] |
Song YJ, Jiang ZH, Wang YH et al. Changes of development and utilization types within the water storage area of Luoma Lake in Xinyi city and their causes. Technology Innovation and Application, 2021, 11(36): 46-49. [宋亚君, 蒋志昊, 王轶虹等. 新沂市骆马湖蓄水范围内开发利用类型变化及原因分析. 科技创新与应用, 2021, 11(36): 46-49. DOI:10.19981/j.CN23-1581/G3.2021.36.012] |
| [21] |
Chidepudi SKR, Massei N, Jardani A et al. A wavelet-assisted deep learning approach for simulating groundwater levels affected by low-frequency variability. Science of the Total Environment, 2023, 865: 161035. DOI:10.1016/j.scitotenv.2022.161035 |
| [22] |
Huang XY, Gao MY, Wang JD et al. Long-term succession patterns and driving factors of water quality in a flood-pulse system lake: A case study of Lake Luoma, Jiangsu Province. Environmental Science, 2023, 44(1): 219-230. [黄雪滢, 高鸣远, 王金东等. 过水性湖泊水质长期演变趋势及驱动因素: 以骆马湖为例. 环境科学, 2023, 44(1): 219-230. DOI:10.13227/j.hjkx.202203097] |
| [23] |
Gao ZY, Chen JY, Wang GQ et al. A novel multivariate time series prediction of crucial water quality parameters with Long Short-Term Memory (LSTM) networks. Journal of Contaminant Hydrology, 2023, 259: 104262. DOI:10.1016/j.jconhyd.2023.104262 |
| [24] |
Theodosiou M. Forecasting monthly and quarterly time series using STL decomposition. International Journal of Forecasting, 2011, 27(4): 1178-1195. DOI:10.1016/j.ijforecast.2010.11.002 |
| [25] |
Lin MD, Liu PY, Huang CW et al. The application of strategy based on LSTM for the short-term prediction of PM2.5 in city. Science of the Total Environment, 2024, 906: 167892. DOI:10.1016/j.scitotenv.2023.167892 |
| [26] |
Cahuantzi R, Chen XY, Güttel S. A comparison of LSTM and GRU networks for learning symbolic sequences. Science and Information Conference. Cham: Springer, 2023: 771-785. DOI:10.1007/978-3-031-37963-5_53
|
| [27] |
Lundberg S, Lee SI. A unified approach to interpreting model predictions. ArXiv e-Prints, 2017: arXiv: 1705.07874. DOI: 10.48550/arXiv.1705.07874.
|
| [28] |
Díaz-Rodríguez N, Lamas A, Sanchez J et al. EXplainable Neural-Symbolic Learning (X-NeSyL) methodology to fuse deep learning representations with expert knowledge graphs: The MonuMAI cultural heritage use case. Information Fusion, 2022, 79: 58-83. DOI:10.1016/j.inffus.2021.09.022 |
| [29] |
Mubarak H, Hammoudeh A, Ahmad S et al. A hybrid machine learning method with explicit time encoding for improved Malaysian photovoltaic power prediction. Journal of Cleaner Production, 2023, 382: 134979. DOI:10.1016/j.jclepro.2022.134979 |
| [30] |
Wang SN, Li RP, Wu YJ et al. Estimation of surface soil moisture by combining a structural equation model and an artificial neural network (SEM-ANN). Science of the Total Environment, 2023, 876: 162558. DOI:10.1016/j.scitotenv.2023.162558 |
| [31] |
Maaz TM, Heck RH, Glazer CT et al. Measuring the immeasurable: A structural equation modeling approach to assessing soil health. Science of the Total Environment, 2023, 870: 161900. DOI:10.1016/j.scitotenv.2023.161900 |
| [32] |
McDonald RP, Ho MH R. Principles and practice in reporting structural equation analyses. Psychological Methods, 2002, 7(1): 64-82. DOI:10.1037/1082-989x.7.1.64 |
| [33] |
Al Shehhi MR, Kaya A. Time series and neural network to forecast water quality parameters using satellite data. Continental Shelf Research, 2021, 231: 104612. DOI:10.1016/j.csr.2021.104612 |
| [34] |
Wang H, Lei RY, Fan DL et al. Simulation and optimum control of total phosphorus in flood season of Luoma Lake based on MIKE21. The Administration and Technology of Environmental Monitoring, 2023, 35(6): 65-70. [王辉, 雷蕊宇, 樊冬玲等. 基于MIKE21的骆马湖汛期总磷模拟及优化调控研究. 环境监测管理与技术, 2023, 35(6): 65-70.] |
| [35] |
Wang KY, Zhang LM, Fu XL. Time series prediction of tunnel boring machine (TBM) performance during excavation using causal explainable artificial intelligence (CX-AI). Automation in Construction, 2023, 147: 104730. DOI:10.1016/j.autcon.2022.104730 |
| [36] |
Ding YX, Yi QT, Jia QR et al. Quantifying phosphorus levels in water columns equilibrated with sediment particles in shallow lakes: From algae/cyanobacteria-available phosphorus pools to pH response. Science of the Total Environment, 2023, 868: 161694. DOI:10.1016/j.scitotenv.2023.161694 |
| [37] |
Li Y, Xiao HH, Zhao YY et al. Study on total phosphorus pollution load estimation and prevention and control countermeasures in Dongting Lake. Energy Reports, 2023, 9: 294-305. DOI:10.1016/j.egyr.2023.04.272 |
| [38] |
Ji NN, Liu Y, Wang SR et al. Buffering effect of suspended particulate matter on phosphorus cycling during transport from rivers to lakes. Water Research, 2022, 216: 118350. DOI:10.1016/j.watres.2022.118350 |
| [39] |
Bai XL, Zhou YK, Ye WN et al. Response of organic phosphorus in lake water to environmental factors: A simulative study. Science of the Total Environment, 2021, 785: 147275. DOI:10.1016/j.scitotenv.2021.147275 |
| [40] |
Lu H, Yang LY, Fan YF et al. Novel simulation of aqueous total nitrogen and phosphorus concentrations in Taihu Lake with machine learning. Environmental Research, 2022, 204: 111940. DOI:10.1016/j.envres.2021.111940 |
| [41] |
Lee HW, Kim M, Son HW et al. Machine-learning-based water quality management of river with serial impoundments in the Republic of Korea. Journal of Hydrology: Regional Studies, 2022, 41: 101069. DOI:10.1016/j.ejrh.2022.101069 |
| [42] |
Zhang YT, Li CL, Jiang YQ et al. A hybrid model combining mode decomposition and deep learning algorithms for detecting TP in urban sewer networks. Applied Energy, 2023, 333: 120600. DOI:10.1016/j.apenergy.2022.120600 |
 2024, Vol. 36
2024, Vol. 36 

