(2: 南京信息工程大学水利部水文气象灾害机理与预警重点实验室, 南京 210044)
(3: 河海大学水灾害防御全国重点实验室, 南京 210098)
(4: 南昌工程学院水利与生态工程学院, 南昌 330099)
(2: Key Laboratory of Hydrometeorological Disaster Mechanism and Warning of Ministry of Water Resources, Nanjing University of Information Science & Technology, Nanjing 210044, P.R.China)
(3: The National Key Laboratory of Water Disaster Prevention, Hohai University, Nanjing 210098, P.R.China)
(4: School of Hydraulic and Ecological Engineering, Nanchang Institute of Technology, Nanchang 330099, P.R.China)
径流模拟预测是水资源规划管理的基础。由于气候变化以及人类活动影响[1-2],降雨径流过程表现出高度的非线性以及不稳定性,降雨径流过程的准确预测难度较大[3-4]。
降雨径流模拟模型主要分为基于过程驱动的模型和基于数据驱动的模型两大类[5]。基于过程驱动的水文模型具有一定的物理意义,但是由于对水文过程机制的认识存在一定程度上的不足且模型的复杂程度高、参数多[6-7],使得物理水文模型在实际应用中存在很大挑战[8]。随着3S技术的逐步发展以及地球大数据的形成,数据驱动水文模型不需要考虑径流形成的实际物理意义,仅通过挖掘输入和输出数据的相关联系对径流进行预测,一些研究显示,机器学习模型对径流序列的分析预测具有一定优势[6, 9]。其中长短时记忆神经网络(LSTM)在处理时间序列预测问题具有优越性,在水文领域受到了广泛关注[10-11]。Kratzert等[12]将LSTM模型与萨克拉门托(SAC-SMA)模型应用于241个集水区,进行降雨径流预测,结果表明LSTM模型在水文预测中具有更好的模拟效果。殷兆凯等[13]利用LSTM模型针对不同预见期,建立了流域降雨径流预测模型,并将其模拟结果与新安江模型的模拟结果进行对比,发现在相同预见期下LSTM模型的预测精度均高于新安江模型。田烨等[14]采用LSTM及其变体模型在湘江流域进行日径流预测,发现相比模型结构的差异,输入变量的改变对预测效果的影响更大。
对于径流预测模型的优化,主要体现在延长模型的预见期以及提高模型的预测精度两方面[15]。而对于神经网络模型,延长其有效预见期较难[16-17],徐源浩等[18]利用LSTM模型探讨其在黄河中游暴雨洪水预报的效果,发现当预见期大于6 h时,即使增加了模型的神经元数量以及训练次数,模拟精度的提升不明显。林康聆等[17]将LSTM模型及与Encoder-Decoder结构耦合的模型(LSTM-ED)应用于建溪流域,认为模型的有效预见期与研究流域的最大汇流时间密切相关。但当在不同的情景下进行降雨径流预测时,神经网络模型的有效预见期与流域平均产汇流时间之间的关系仍有待研究。
为了提高机器学习模型的径流预测精度,现有研究多通过优化模型的框架[19]或者采用参数优化方法对模型的超参数[20]进行优化。但是鲜有研究考察模型的记忆时间对模型性能的影响,模型的性能与输入记忆时间之间的关系是值得研究的问题[21]。Gao等[21]采用人工神经网络(ANN)、门控循环单元(GRU)以及LSTM模型对沙溪流域的径流进行模拟研究,结果表明LSTM和GRU的预测精度随记忆时间的延长而增加,最终趋于稳定。Wei等[22]在长江流域采用LSTM、GRU以及Transformer模型探究不同长度的记忆时间与模型性能之间的关系,结果表明适宜的记忆时间可以显著提高模型的预测精度,且不同长度的预见期可能会对应不同的记忆时间。范宏翔等[23]利用LSTM模型探究了鄱阳湖流域不同记忆时间下径流预测效果,表明在鄱阳湖流域使用10 d的记忆时间较为合理。但上述研究均未探究LSTM模型不同预见期长度与对应的最佳记忆时间之间的联系,以及当流域面积不同时,不同预见期下的模型预测精度与其记忆时间之间的关系。
鄱阳湖为我国最大的淡水湖泊,但是由于气候环境的快速变化以及人类活动的影响,水文变异过程明显[24]。而赣江流域地形成分复杂,山地、低丘和丘陵约占流域总面积的96%,是鄱阳湖流域最大的子流域,因而其径流研究受到广泛关注[25-26]。
综上所述,本文旨在:(1)利用LSTM模型在赣江流域构建3种情景下的径流预测模型,探讨预见期延长后不同情景下模型预测精度的变化以及不同情景下神经网络径流预测的有效预见期与流域平均产汇流时间的关系;(2)探究当流域面积不同时,不同预见期下LSTM模型的预测精度与记忆时间之间有何联系,以及当预见期延长后模型达到最佳模拟效果所需的记忆时间有何变化。研究结果将提高赣江流域径流预测精度,对LSTM径流预测模型的有效预见期以及最佳记忆时间的研究提供新思路。
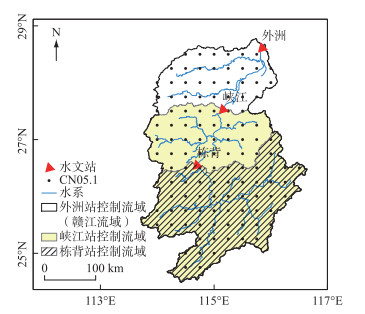
1 研究区域及数据 1.1 研究区概况赣江是长江八大支流之一,是鄱阳湖水系中最大的河流,主河道长823 km。赣江流域(24°29′~29°11′N,113°30′~116°40′E)位于长江中下游右岸,属于中亚热带湿润季风气候区,流域多年平均降水量1580 mm,时空分布不均匀,具有明显的季节性,主要集中在4—6月,径流主要由降水补给。为探究不同流域面积与LSTM模型的有效预见期以及所需记忆时间之间的关系,分别选取外洲站、峡江站、栋背站的集水区域进行探究,不同站点的流域面积大小见表 1,研究区域示意图见图 1。
| 表 1 研究区域控制站数据资料 Tab. 1 Data information of control station in research area |
|
图 1 研究区域地理位置 Fig.1 Geographical location of the study area |
本研究选取日尺度CN05.1格点降水和站点实测逐日径流资料。其中CN05.1是基于2400余个中国地面气象台的观测资料,采用距平逼近法建立的格点化观测数据集[27],在多个流域水文模拟中的适用性较好[28-30],在研究区域的分布见图 1,采用算数平均法计算面平均降水量。由于训练集和验证集的分布需要保持一定的一致性,而降水和径流量在年内变化具有相似性[31],故按照年份长度进行训练集和验证集的划分。取不同站点年份长度的前80%用来训练模型参数,后20%数据作为验证集,不同站点的训练集和验证集划分见表 1。
2 研究方法 2.1 LSTM模型LSTM是Hochreiter和Schmidhuber[32]为了解决传统循环神经网络存在的梯度爆炸和梯度消失问题的提出的深度学习模型。由于其特殊的结构,广泛应用于长时间序列数据的模拟。利用LSTM模型进行径流模拟的步骤可参考Kratzert等[12]。参照Ravindra[33]和殷兆凯等[13]对模型结构进行设置,并采用试算法,将隐藏层数设置为1,初始学习率设置为0.005,丢失率采用0.01,隐藏层神经单元数量取值为128。模型采用自适应矩估计(Adam)算法训练优化,为了防止过拟合现象的发生,学习率在训练过程中递减。采用均方根误差(RMSE)作为优化过程的目标函数,最大迭代次数设置为250。
由于降水资料和径流资料在量级上相差较大,为了减少由于权重带来的影响并加快模型的计算速度,故采用线性函数归一化(正向)方法进行处理。
正向归一化:
| x′1=x−xmin | (1) |
逆向归一化:
| x_2^{\prime}=\frac{x_{\max }-x}{x_{\max }-x_{\min }} | (2) |
式中,x′1表示经过正向归一化后的数据,x′2表示经过逆向归一化后的数据;x表示原始数据;xmin和xmax分别表示原始数据中的最小值和最大值。
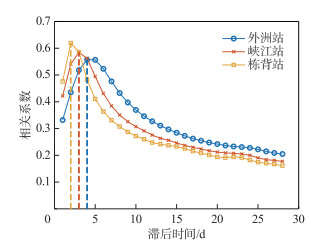
2.2 情景设置表 2为基于不同输入变量设计的3种不同情景。根据相关系数最大值对应的滞时可以估算出不同流域的平均产汇流时间[34-35],通过图 2不同滞时的降水和径流之间的相关系数,可以推测研究区域的最大平均产汇流时间为5 d以内。同时,根据范宏翔等[23]对鄱阳湖的赣江、抚河、信江等5个子流域LSTM模型记忆时间的探讨,发现当记忆时间超过10 d后,RMSE值会迅速增大,超过15 d后纳什效率系数(NSE)会迅速下降。
| 表 2 情景设置 Tab. 2 Scenario settings |
|
图 2 不同滞时的降水与流量的相关系数 Fig.2 Correlation coefficient diagram of precipitation and flow at different lag times |
因此,分别将预见期、记忆时间以及输入变量进行组合,3种情景下均考虑预见期1~6 d,并在每个预见期下同时探究记忆时间分别为1、2、3、4、5、7、14、21 d(其中1~5 d的设置是为详细探究不同面积流域平均产汇流时间与其对应的最佳记忆时间之间的关系,7、14、21 d是以周为单位充分探讨模型预测精度与记忆时间之间的关系)时模型的模拟效果。模型输出结果为不同站点对应的日径流量。
2.3 评价指标本文采用NSE、RMSE以及平均绝对误差(MAE)3个统计指标(具体计算公式见附表Ⅰ)对模型的模拟效果进行评价,为了更清晰地了解记忆时间对模型的预测精度的影响,对同一站点及预见期下不同记忆时间预测结果的NSE进行正向归一化,RMSE和MAE值进行逆向归一化(式(2)),再将3个指标同时取算数平均值,作为综合评价指标(ENRM)。为了评价不同情景之间的预测效果,将不同情景的平均下降率α进行比较(以情景S1和S2为例),其具体计算公式如下:
| E_{\mathrm{NRM}}=\frac{1}{3}[\operatorname{MMS}(N S E)+\operatorname{NMMS}(R M S E)+\operatorname{NMMS}( { MAE })] | (3) |
| \alpha=100 \% \times \frac{1}{6} \sum\limits_{i=1}^6 \frac{N S E_{i, \text { 外州站 } S 1}-N S E_{i, \text { 外州站 } S 2}}{N S E_{i, \text { 外州站 } S 1}} | (4) |
式中,MMS(x)和NMMS(x)分别表示正向归一化和逆向归一化;ENRM处于[0, 1]之间,且其值越接近于1,表示预测效果越好。
3 结果 3.1 日径流模拟结果不考虑记忆时间对模型有效预见期的影响时,选取每个预见期不同记忆时间下模型模拟效果的最优值(表 3),对不同流域面积下模型有效预见期进行探究。
| 表 3 不同预见期下日径流模拟结果的NSE* Tab. 3 NSE of daily runoff simulation results under different lead times |
由表 3可知,当预见期相同时,不同流域面积下情景S1的模拟效果均优于情景S2及S3。综合来看,当预见期为1~6 d时,外洲站情景S2较S1的NSE平均下降率为28.05%,情景S3较情景S1的NSE平均减小了13.35%;峡江站情景S2和S3较情景S1的NSE平均减小了69.21%和30.88%;栋背站情景S2较情景S1的NSE平均减小了214.45%,情景S3较情景S1减小了68.94%。故整体来看,3种情景的预测精度由高至低依次为:情景S1>情景S3>情景S2。
当预见期为1 d时,情景S2的模拟效果优于情景S3的径流模拟效果,说明2种径流影响因子的重要性:前期径流大于降水。随着预见期的延长,不同情景下3个控制站点的模拟精度均呈下降趋势。据表 3不同情景下NSE值随着预见期延长的平均下降率,可知,情景S1的平均下降率为50.30%~131.48%,情景S2的平均下降率为84.54%~157.31%,情景S3的平均下降率为58.93%~146.88%。由于情景S1同时考虑降水以及前期径流、情景S2和S3分别仅采用前期径流或者降水对径流进行预测,据此可以区分降水和径流对径流预测精度的影响:随着预见期的延长,降水对预测精度的影响逐渐提升,前期径流较降水对径流预测效果的影响逐渐下降。同时,随着流域面积的增大,不同情景下,随着预见期的延长,平均下降率均减小,可见,流域面积越大,径流预测效果越好。
当NSE≥0.65时,预报精度达到可接受的程度[36]。以此为标准,可知,在情景S1和S3下,外洲站的有效预见期均为4 d,峡江站有效预见期均为3 d,栋背站有效预见期均为2 d;在情景S2下,外洲站、峡江站、栋背站的有效预见期分别为3、2和1 d。由图 2可知,外洲站、峡江站、栋背站控制流域的平均产汇流时间大致分别为4、3、2 d,与情景S1和S3得出的有效预见期相近。而在情景S2下,有效预见期均小于情景S1和S3得出的有效预见期以及流域的平均产汇流时间,可能是由于径流序列的自相关性随着时间的延长而减小[37],且情景S2缺乏降水信息导致的。综上可知,降水的输入能够有效延长LSTM径流预测模型的有效预见期。
3.2 记忆时间对LSTM模型的影响在3个情景中,情景S1的径流预测效果最好,故以情景S1为例,探究在有效预见期内,记忆时间对径流模拟结果的影响以及预见期与其对应的最佳记忆时间之间的关系。
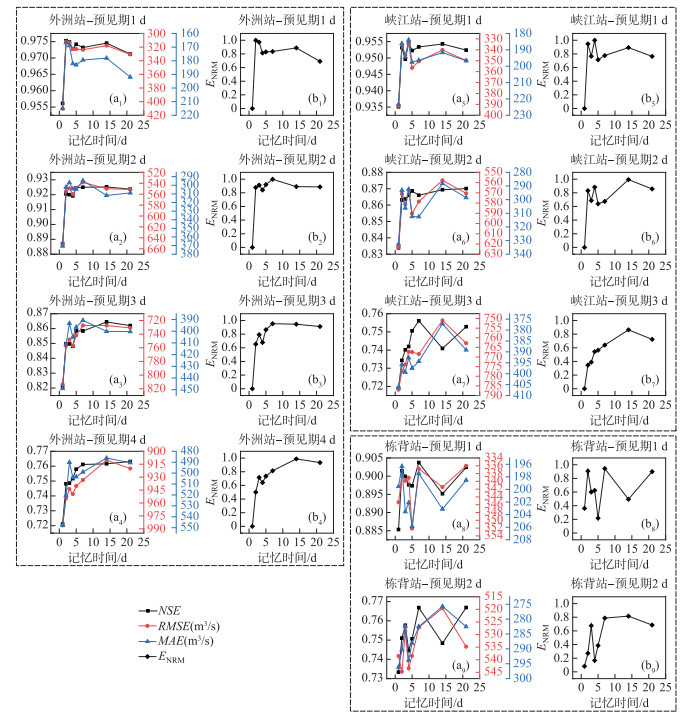
3.2.1 不同记忆时间下径流预测精度图 3(a1~a4)(a5~a7)(a8~a9)分别表示LSTM模型在外洲站、峡江站、栋背站考虑记忆时间为1、2、3、4、5、7、14、21 d时,不同预见期下径流预测的结果。以外洲站为例,不同记忆时间下评价指标值见表 4。
|
图 3 3个站点不同预见期以及记忆时间下的预测效果 Fig.3 The prediction effect of three sites under different lead times and time steps |
| 表 4 外洲站考虑不同记忆时间的预测效果变化范围 Tab. 4 The variation range of prediction effect at Waizhou Station considering different lead times |
以记忆时间为1 d和最佳记忆时间的预测结果对比为例,不同预见期下外洲站的NSE增大了2.00%~5.62%,RMSE减小了7.67%~24.03%,MAE减小了11.27%~22.44%;峡江站的NSE提高了2.08%~4.26%,RMSE和MAE分别减小了4.57%~14.69%、7.13%~17.60%;栋背站的NSE提高了2.05%~2.08%,RMSE和MAE的减幅分别为2.49%~3.52%、1.03%~6.88%。可见,适宜的记忆时间能够有效提高LSTM模型的径流预测精度。
图 3(b1~b9)为3个站点在不同预见期下随记忆时间延长,其综合指标ENRM的变化曲线。整体来看,随着记忆时间的延长,ENRM先上升达到最大值后下降,最后逐渐趋于稳定。
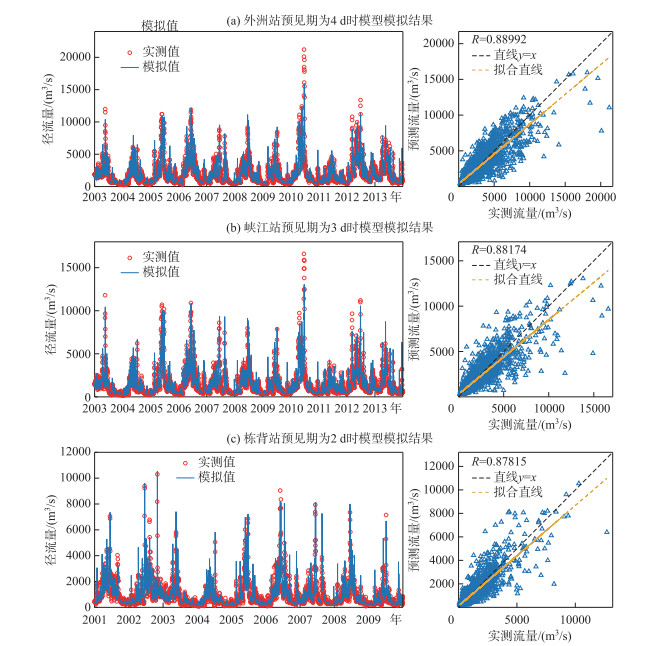
3.2.2 最佳记忆时间下径流模拟结果图 4列出了情景S1下,LSTM模型在3个站点最长有效预见期与其对应的最佳记忆时间(14 d)验证期的径流过程线及散点图。3个站点径流预测过程与实测径流过程总体上较为相近,小流量部分与实测值的拟合程度较好,散点图的大流量均有少部分位于1 ∶1线下,表明大流量部分存在不同程度的低估现象。但是整体来看,当外洲站预见期为4 d、峡江站预见期为3 d、栋背站预见期为2 d时,实测值与预测值之间的相关性仍然较好,相关系数均在0.87以上。
|
图 4 记忆时间为14 d时验证期径流过程及散点图 Fig.4 The runoff process and scatter plot in the verification period when the time step is 14 days |
为探究不同流域的预见期与对应的最佳记忆时间之间的关系,表 5列出了每个站点不同预见期对应的最佳记忆时间。可见,在有效预见期内,随着预见期的延长,所需的记忆时间均具有上升趋势,不同流域面积下最长有效预见期对应的最佳记忆时间均为14 d,可以认为当采用LSTM模型对赣江流域进行径流预测时,所需的最大记忆时间在14 d左右。当预见期相同时,随着流域面积增大,LSTM径流模拟模型所需的记忆时间越短。
| 表 5 不同预见期对应最佳记忆时间 Tab. 5 The best time steps corresponding to different lead times |
利用机器学习模型对径流进行预测时,输入变量对径流预测结果的影响较大。田烨等[14]采用排列重要法分析径流预测结果,发现降水和历史径流2种影响因子较为重要,且随着预见期的延长,历史径流的重要性逐渐下降,降水的重要性有所增加。同样,本文通过将不同预见期下情景S2和情景S3的径流预测效果进行比较,可以推测降水较前期径流对流域出口径流量的影响时滞更长。通过分析外洲站、峡江站以及栋背站的日径流变化过程,发现外洲站变差系数为1.03,偏态系数2.62;峡江站变差系数为1.12,偏态系数3.16;栋背站变差系数1.17,偏态系数3.71。可知随着流域面积的增大,站点径流的变差系数和偏态系数均呈下降趋势。可能是由于流域面积的增大,流域调蓄作用增加、推移坦化作用更加明显,所以径流序列更加平稳。同时,郭玉雪等[11]发现当输入变量中未引入气象预报信息时,LSTM等3种RNN模型对平稳数据的模拟效果更好。所以在3种情景下,随着流域面积的增大,径流预测精度均有所提升。
目前,LSTM模型作为径流预测的代表性机器学习模型,其记忆时间多由试错法[38]或直接采用流域平均产汇流时间[34]确定。将流域平均产汇流时间作为记忆时间具有一定物理意义,但是可能由于机器学习模型的黑箱属性,当采用LSTM模型在不同面积的流域上进行径流预测时,发现LSTM模型在不同流域对应的最佳记忆时间与该流域的平均产汇流时间不同。且在同一预见期下,随着流域面积增大,LSTM模型对应的最佳记忆时间均有所减小,这可能是由不同站点径流序列的自相关性之间存在差异导致的。由图 5可知,滞时相同时,3个站点的径流自相关系数由大至小依次为:外洲站>峡江站>栋背站,据此可以推测:当流域面积增大时,由于径流序列的自相关性增大,达到一定预测精度所需的记忆时间减小。
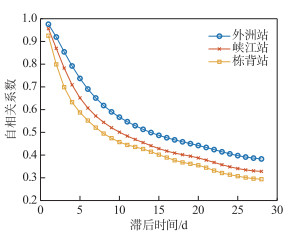
|
图 5 不同滞时的径流自相关图 Fig.5 Autocorrelation coefficients diagram of runoff with different lag times |
通过分析3个站点不同预见期与其对应的最佳记忆时间之间的关系,发现不同面积的流域,随着预见期的延长,所对应的最佳记忆时间均具有上升趋势,可能是由于预见期的延长,导致输入和输出数据之间的时间间隔增大[39],LSTM模型难以挖掘两者之间的相关关系,而更长的记忆时间可以带来更多径流预测的有效信息。另外,通过探究不同预见期下模型预测精度与记忆时间之间的关系,发现模型的预测效果随着记忆时间的延长具有增长趋势,可能是由于机器学习模型除了从降水径流数据中挖掘到相关关系,土壤湿度等与产流相关的信息可能已经被间接表示[40]。但是过长的记忆时间并非能带来更好的预测效果,达到最佳记忆时间之后,继续延长记忆时间反而会使得模型的预测效果变差,这可能是由于无关输入引入了较大的噪声,对模型的预测精度有所影响[40]。Wei等[22]也有相似的发现,当采用LSTM和GRU模型对长江流域进行径流预测时,发现随着记忆时间的延长,模型的预测性能呈现先上升后下降的趋势。
刘成帅等[39]和Xu等[41]均发现当预见期延长后,LSTM模型对洪峰的预测存在低估现象,图 4为在不同站点下最长有效预见期下径流预测结果,发现径流预测结果在大流量部分呈现不同程度的低估现象,推测是预见期的延长导致的。
根据刘磊等[42]在鄱阳湖流域采用GN算法对水文站网进行径流相似性分区,发现外洲、峡江以及栋背站不论在何种等级R统计量阈值下,均可以划分为同一水文相似区。且通过对预见期与最佳记忆时间之间关系进行讨论后发现:不同面积流域LSTM径流预测模型在最长有效预见期下,对应的最佳记忆时间均为14 d。可能由于3个站点的径流具有一定的相似性,所以当达到最长有效预见期时对应的最佳记忆时间相同。
本文探究得出的LSTM模型在赣江流域的最佳记忆时间为14 d,而范宏翔等[23]采用LSTM构建气象-径流模型,利用降水、气温、太阳辐射、相对湿度以及近地面风速进行日径流预测,综合考虑模型的计算效率及效果后,认为10 d作为鄱阳湖流域的记忆时间较合理,与本探究有所不同,可能是进行径流预测时情景设置的不同导致的。
5 结论本研究基于LSTM模型对赣江流域的3个流域进行径流预测,设置3种情景,分析记忆时间的不同对不同预见期下的径流预测精度的影响,得出以下结论:
1) 同时输入降水及前期径流信息在3个站点的预测效果均较好,且与仅考虑降水的情景有效预见期相同。两种情景下的有效预见期均与估算的流域平均产汇流时间相同。
2) 随着预见期的延长,前期径流对径流预测效果的影响小于降水信息对径流预测结果的影响。随着流域面积的增加,不同情景下径流预测精度均提高。
3) 合适的记忆时间可以有效提高LSTM模型模拟径流的精度。当预见期相同时,预测精度随记忆时间的变化规律大致为:随着预见期的延长,预测精度先上升达到最佳后逐步下降,然后趋于稳定。
4) 在有效预见期内,随着预见期的增加,采用LSTM模型对不同面积的流域进行径流预测时所需的记忆时间均具有上升趋势,且可以估计在赣江流域进行径流预测时,最佳记忆时间在14 d左右。
6 附录附表Ⅰ见电子版(DOI: 10.18307/2024.0454)。
| 附表Ⅰ 评价指标 Appendix Ⅰ List of evaluation indicates |
| [1] |
Jin JX, Xiao YY, Jin JL et al. Spatial-temporal variabilities of the contrasting hydrometeorological extremes and the impacts on vegetation growth over the Yangtze River basin. Advances in Water Science, 2021, 32(6): 867-876. [金佳鑫, 肖园园, 金君良等. 长江流域极端水文气象事件时空变化特征及其对植被的影响. 水科学进展, 2021, 32(6): 867-876.] |
| [2] |
Jiang T, Sun HM, Li XC et al. Impact of climate change on water cycle. Meteorological Monthly, 2020, 46(3): 289-300. [姜彤, 孙赫敏, 李修仓等. 气候变化对水文循环的影响. 气象, 2020, 46(3): 289-300. DOI:10.7519/j.issn.1000-0526.2020.03.001] |
| [3] |
Jiang XL, Gupta HV, Liang ZM et al. Toward improved probabilistic predictions for flood forecasts generated using deterministic models. Water Resources Research, 2019, 55(11): 9519-9543. DOI:10.1029/2019wr025477 |
| [4] |
Jiang XL, Zhang LP, Liang ZM et al. Study of early flood warning based on postprocessed predicted precipitation and Xinanjiang model. Weather and Climate Extremes, 2023, 42: 100611. DOI:10.1016/j.wace.2023.100611 |
| [5] |
Zhang K, Niu JF, Li X et al. Comparison of artificial intelligence flood forecasting models in China's semi-arid and semi-humid regions. Water Resources Protection, 2021, 37(1): 28-35, 60. [张珂, 牛杰帆, 李曦等. 洪水预报智能模型在中国半干旱半湿润区的应用对比. 水资源保护, 2021, 37(1): 28-35, 60. DOI:10.3880/j.issn.1004-6933.2021.01.005] |
| [6] |
Li B, Tian FQ, Li YK et al. Development of a spatiotemporal deep-learning-based hydrological model. Advances in Water Science, 2022, 33(6): 904-913. [李步, 田富强, 李钰坤等. 融合气象要素时空特征的深度学习水文模型. 水科学进展, 2022, 33(6): 904-913.] |
| [7] |
Rui XF. Hydrology and big data. Advances in Science and Technology of Water Resources, 2016, 36(3): 1-4. [芮孝芳. 水文学与"大数据". 水利水电科技进展, 2016, 36(3): 1-4. DOI:10.3880/j.issn.1006-7647.2016.03.001] |
| [8] |
Xiong Y, Zhou JZ, Sun N et al. Monthly runoff prediction based on self-adaptive variational mode decomposition and long short-term memory network. Journal of hydraulic Engineering, 2023, 54(2): 172-183, 198. [熊怡, 周建中, 孙娜等. 基于自适应变分模态分解和长短期记忆网络的月径流预报. 水利学报, 2023, 54(2): 172-183, 198.] |
| [9] |
Lees T, Buechel M, Anderson B et al. Benchmarking data-driven rainfall-runoff models in Great Britain: A comparison of long short-term memory (LSTM)-based models with four lumped conceptual models. Hydrology and Earth System Sciences, 2021, 25(10): 5517-5534. DOI:10.5194/hess-25-5517-2021 |
| [10] |
Frame JM, Kratzert F, Klotz D et al. Deep learning rainfall-runoff predictions of extreme events. Hydrology and Earth System Sciences, 2022, 26(13): 3377-3392. DOI:10.5194/hess-26-3377-2022 |
| [11] |
Guo YX, Xu YP, Chen H et al. Reservoir inflow forecasting for island areas based on multiple recurrent neural networks. Journal of Hydroelectric Engineering, 2021, 40(9): 14-26. [郭玉雪, 许月萍, 陈浩等. 基于多种递归神经网络的海岛水库径流预报. 水力发电学报, 2021, 40(9): 14-26. DOI:10.11660/slfdxb.20210902] |
| [12] |
Kratzert F, Klotz D, Brenner C et al. Rainfall-runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrology and Earth System Sciences, 2018, 22(11): 6005-6022. DOI:10.5194/hess-22-6005-2018 |
| [13] |
Yin ZK, Liao WH, Wang RJ et al. Rainfall-runoff modelling and forecasting based on long short-term memory(LSTM). South-to-North Water Transfers and Water Science & Technology, 2019, 17(6): 1-9, 27. [殷兆凯, 廖卫红, 王若佳等. 基于长短时记忆神经网络(LSTM)的降雨径流模拟及预报. 南水北调与水利科技, 2019, 17(6): 1-9, 27.] |
| [14] |
Tian Y, Tan WL, Wang GQ et al. Performance of variant LSTM models in runoff prediction and their interpretability. Water Resources Protection, 2023, 39(3): 188-194. [田烨, 谭伟丽, 王国庆等. LSTM变体模型在径流预测中的性能及其可解释性. 水资源保护, 2023, 39(3): 188-194. DOI:10.3880/j.issn.1004-6933.2023.03.023] |
| [15] |
Wen YH, Li ZJ, Sun MK et al. Influence of rainfall input on real-time flood forecasting accuracy and forecast period. J Lake Sci, 2019, 31(1): 39-51. [温娅惠, 李致家, 孙明坤等. 降雨输入对实时洪水预报精度与预见期的影响. 湖泊科学, 2019, 31(1): 39-51. DOI:10.18307/2019.0104] |
| [16] |
Cardenas-Barrera JL, Meng JL, Castillo-Guerra E et al. A neural network approach to multi-step-ahead, short-term wind speed forecasting. In: 2013 12th International Conference on Machine Learning and Applications. Miami, FL, USA. IEEE, 2013: 243-248. DOI: 10.1109/ICMLA.2013.130.
|
| [17] |
Lin KL, Chen H, Chen QY et al. Research on LSTM runoff forecast model coupled with Encoder-Decoder. Engineering Journal of Wuhan University, 2022, 55(8): 755-761. [林康聆, 陈华, 陈清勇等. 耦合Encoder-Decoder的LSTM径流预报模型研究. 武汉大学学报: 工学版, 2022, 55(8): 755-761. DOI:10.14188/j.1671-8844.2022-08-001] |
| [18] |
Xu YH, Wu Q, Li CQ et al. Simulation of the flood process in the middle reaches of the Yellow River by a long-short term memory(LSTM) neuro network. Journal of Beijing Normal University: Natural Science, 2020, 56(3): 387-393. [徐源浩, 邬强, 李常青等. 基于长短时记忆(LSTM)神经网络的黄河中游洪水过程模拟及预报. 北京师范大学学报: 自然科学版, 2020, 56(3): 387-393.] |
| [19] |
Cui Z, Guo SL, Wang Y et al. Deep learning model for probability forecasting of flood to Three Gorges Reservoir. Journal of Hydroelectric Engineering, 2023, 42(4): 1-10. [崔震, 郭生练, 汪芸等. 三峡入库洪水概率预报的深度学习模型. 水力发电学报, 2023, 42(4): 1-10. DOI:10.11660/slfdxb.20230401] |
| [20] |
Guo TL, Song SB, Zhang T et al. A new stepwise decomposition ensemble model based on two-stage particle swarm optimization algorithm for the runoff prediction. Journal of hydraulic Engineering, 2022, 53(12): 1456-1466. [郭田丽, 宋松柏, 张特等. 基于两阶段粒子群优化算法的新型逐步分解集成径流预测模型. 水利学报, 2022, 53(12): 1456-1466.] |
| [21] |
Gao S, Huang YF, Zhang S et al. Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation. Journal of Hydrology, 2020, 589: 125188. DOI:10.1016/j.jhydrol.2020.125188 |
| [22] |
Wei XK, Wang GJ, Schmalz B et al. Evaluation of Transformer model and Self-Attention mechanism in the Yangtze River Basin runoff prediction. Journal of Hydrology: Regional Studies, 2023, 47: 101438. DOI:10.1016/j.ejrh.2023.101438 |
| [23] |
Fan HX, He HD, Xu LG et al. Simulation and attribution analysis based on the long-short-term-memory network for detecting the dominant cause of runoff variation in the Lake Poyang Basin. J Lake Sci, 2021, 33(3): 866-878. [范宏翔, 何菡丹, 徐力刚等. 基于长短记忆模型的鄱阳湖流域径流模拟及其演变的归因分析. 湖泊科学, 2021, 33(3): 866-878. DOI:10.18307/2021.0319] |
| [24] |
Cao YX, Xu LG, Fan HX et al. Impact of climate change and human activities on the changes of ecological flow indicators in the Lake Poyang Basin since 1960s. J Lake Sci, 2022, 34(1): 232-246. [曹宇贤, 徐力刚, 范宏翔等. 1960年以来气候变化与人类活动对鄱阳湖流域生态径流改变的影响. 湖泊科学, 2022, 34(1): 232-246. DOI:10.18307/2022.0119] |
| [25] |
Deng PX, Wang YT, Hu QF et al. Application of GR4J in daily runoff simulation for Ganjiang River Basin. Journal of China Hydrology, 2014, 34(2): 60-65. [邓鹏鑫, 王银堂, 胡庆芳等. GR4J模型在赣江流域日径流模拟中的应用. 水文, 2014, 34(2): 60-65.] |
| [26] |
Wang WG, Zou JC, Deng C. Comparison of data assimilation based approach for daily streamflow simulation under multiple scenarios in Ganjiang River Basin. J Lake Sci, 2023, 35(3): 1047-1056. [王卫光, 邹佳成, 邓超. 赣江流域多种数据同化方案的径流模拟比较. 湖泊科学, 2023, 35(3): 1047-1056. DOI:10.18307/2023.0323] |
| [27] |
Wu J, Gao XJ. A gridded daily observation dataset over China region and comparison with the other datasets. Chinese Journal of Geophysics, 2013, 56(4): 1102-1111. DOI: 10.6038g20130406. [吴佳, 高学杰. 一套格点化的中国区域逐日观测资料及与其它资料的对比. 地球物理学报, 2013, 56(4): 1102-1111. ]
|
| [28] |
Wang W, Ju Q, Wang GQ et al. Applicability assessment of CN05.1 gridded precipitation dataset in Weihe River Basin. Journal of China Hydrology, 2022, 42(6): 88-92. [王维, 鞠琴, 王国庆等. CN05.1格点降水数据在渭河流域适用性评估及应用. 水文, 2022, 42(6): 88-92.] |
| [29] |
Luo YX, Xu CC, Chu Z et al. Application of CN05.1 meteorological data in watershed hydrological simulation: A case study in the upper reaches of Kaidu River basin. Climate Change Research, 2020, 16(3): 287-295. [罗映雪, 徐长春, 楚智等. CN05.1气象数据在流域水文模拟中的应用——以新疆开都河流域为例. 气候变化研究进展, 2020, 16(3): 287-295.] |
| [30] |
Pan ZR, Li Wei, Guo JH et al. Applicability of CN05.1 reanalysis data in hydrological simulation of remote watershed of Northwest China. Water Resources and Power, 2022, 40(11): 6-9. [潘张榕, 李薇, 郭军红等. CN05.1再分析资料在西北偏远流域水文模拟中的适用性. 水电能源科学, 2022, 40(11): 6-9.] |
| [31] |
Liao M, Zhan ZQ, Guo W et al. Study on rainfall-runoff simulation and prediction in lake basin based on dynamic data-driven deep recurrent network. National Remote Sensing Bulletin, 2019, 23(5): 911-923. [廖明, 詹总谦, 呙维等. 动态数据驱动模式下的湖泊流域降雨径流模拟. 遥感学报, 2019, 23(5): 911-923. DOI:10.11834/jrs.20198027] |
| [32] |
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [33] |
Ravindra B. Forecasting solar radiation duringdust storms using deep learning, 2018. DOI: 10.48550/arXiv.1808.10854[EB/OL].
|
| [34] |
Cui Z, Guo SL, Wang J et al. Probabilistic forecasting of flood processes based on hybrid deep learning models. Journal of hydraulic Engineering, 2023, 54(8): 889-897, 909. [崔震, 郭生练, 王俊等. 基于混合深度学习模型的洪水过程概率预报研究. 水利学报, 2023, 54(8): 889-897, 909.] |
| [35] |
Zhou YL, Cui Z, Lin KL et al. Short-term flood probability density forecasting using a conceptual hydrological model with machine learning techniques. Journal of Hydrology, 2022, 604: 127255. DOI:10.1016/j.jhydrol.2021.127255 |
| [36] |
Ritter A, Muñoz-Carpena R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. Journal of Hydrology, 2013, 480: 33-45. DOI:10.1016/j.jhydrol.2012.12.004 |
| [37] |
Zhao TTG, Yang DW, Cai XM et al. Predict seasonal low flows in the upper Yangtze River using random forests model. Journal of Hydroelectric Engineering, 2012, 31(3): 18-24, 38. [赵铜铁钢, 杨大文, 蔡喜明等. 基于随机森林模型的长江上游枯水期径流预报研究. 水力发电学报, 2012, 31(3): 18-24, 38.] |
| [38] |
Shi PF, Zhao YJ, Xu HR et al. Simulation and prediction of streamflow based on phase space reconstruction and deep learning algorithm. Advances in Water Science, 2023, 34(3): 388-397. [师鹏飞, 赵酉键, 徐辉荣等. 融合相空间重构和深度学习的径流模拟预测. 水科学进展, 2023, 34(3): 388-397.] |
| [39] |
Liu CS, Sun Y, Hu CH et al. Study on flood forecasting model of watershed-urban complex system considering the spatial distribution of runoff generation pattern. Advances in Water Science, 2023, 34(4): 530-540. [刘成帅, 孙悦, 胡彩虹等. 考虑产流模式空间分布的流域-城市复合系统洪水预报模型. 水科学进展, 2023, 34(4): 530-540.] |
| [40] |
Xiang ZR, Yan J, Demir I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resources Research, 2020, 56(1): e2019WR025326. DOI:10.1029/2019wr025326 |
| [41] |
Xu YH, Hu CH, Wu Q et al. Research on particle swarm optimization in LSTM neural networks for rainfall-runoff simulation. Journal of Hydrology, 2022, 608: 127553. DOI:10.1016/j.jhydrol.2022.127553 |
| [42] |
Liu L, Gao C, Wang ZG et al. Study on streamflow similarity regionalization based on nonlinear correlation and complex network. Advances in Water Science, 2022, 33(3): 442-451. [刘磊, 高超, 王志刚等. 基于非线性相关性和复杂网络的径流相似性分区. 水科学进展, 2022, 33(3): 442-451.] |
 2024, Vol. 36
2024, Vol. 36 


