(2: 长江水利委员会长江科学院, 武汉 430015)
(2: Changjiang River Scientific Research Institute, Wuhan 430015, P. R. China)
河流与湖泊的水文连通可以表征河湖之间的水体交换程度与湖泊水位变化特征,也是河湖之间物质、能量及生物体进行交换的主要途径。河流自然连通湖泊的水文、水动力条件变化可归因于水文连通程度的变化,同时也影响河流及湖泊干旱洪水极端事件、水环境状况以及生物群落结构[1-3]。对水文连通的量化研究是河湖水文连通性研究的前提[4],也是河湖生态、水资源管理及水环境修复等领域的热点问题[5-6]。
近年来,基于图论、GIS、景观分析等方法的河网系统水文连通评估日趋完善[7-10],这些方法可以较好地解决区域河网内景观斑块、水文连续性问题,多局限于反映大尺度河流水系的宏观描述[11-12],但对于中尺度河流与湖泊系统水文连通的定量计算与评估较少涉及,直接限制了以水文连通作为关键环境因子研究湖泊水环境变化与水生态演变、河湖物质交换及其生态效应等,也制约了河湖水系连通工程的科学实施。因此,本研究提出适用于河流与湖泊水文连通的量化计算模型,有助于对河湖水文连通状况进行监测与实时预报、支撑河流与湖泊水文连通的演变规律及趋势分析,同时可以推动河湖水文连通度直接作为湖泊生态环境变化的控制因子,对于湖泊演化规律、湖泊保护与治理等具有重要意义。
1 河湖水文连通计算模型目前,对于水文连通的研究整体处于探索阶段,理论稍弱于实践,且尚未形成系统的理论基础和评估方法。在河湖水文连通度的内涵及定义的层面上,国内外观点繁杂,未见统一。Pringle[13]基于水生生态学将水文连通性定义为“在水文循环要素内部和各要素之间,物质、能量和生物体以水为媒介进行迁移和传递的能力”,Western等[14]定义水文连通为“径流及其携带的物质、能量从水系网络源头到流域末端的迁移效率”,夏军等[15]将水文连通定义为“在自然和人工形成的江河湖库水系基础上,维系、重塑或新建满足一定功能目标的水流连接通道,以维持相对稳定的流动水体及其联系的物质循环状况”。针对河湖与湖泊之间的水文连通,基于上述国内外主流观点,本文将河流及湖泊之间的水文连通度定义为“通过河流与湖泊之间的连通通道及水文条件,形成的以水流为载体的物质、能量及生物在河流与湖泊之间的传输过程,对河湖系统相对稳定的满足程度”。总结起来,有如下2个必要条件:(1)河流与湖泊之间有水流及物质流通的通道(水道);(2)能满足特定需求的保持流动的水文条件。
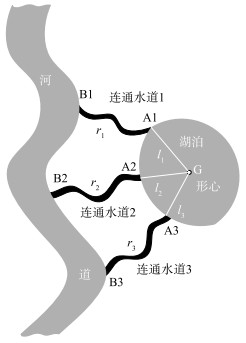
图 1给出了本文提出的河流与湖泊水文连通概化方式,河流与湖泊之间有i条连通水道,每条连通水道与河流及湖泊的连接点分别为Ai、Bi。河流与湖泊之间每条连通水道的水文连通度设为HC,一般作为计算周期为宜,计算周期内连接点Ai的初始水位为本底水位。HC应包含河流与湖泊之间水文连通的必要条件,本文将其定义为3部分:
| HC=α⋅f1⋅f2⋅f3 | (1) |
|
图 1 河流与湖泊水文连通概化图 Fig.1 Schematic diagram of hydrological connectivity between river and lake |
式中,f1表征河流与湖泊之间连通水道的过流能力,取决于本底水位条件下连通水道过流断面面积(A)、湿周(R)及糙率(n),河道水位变化形成的势能是河湖水体交换的主要动力源;f2表征形成河流与湖泊之间水文连通的水文条件,与河道水位变化速率(δH)有关;f3表征河流与湖泊之间水文连通对河湖系统的满足情况,与本底水位条件下湖泊水体容积相关;α为修正系数,当计算周期为天时,α=1,当计算周期为周、旬、月等时,α为天在计算周期内的占比。
河流与湖泊连通水道一般为复式断面,高水位时漫滩过水,低水位时主河槽过水,水流一般为均匀流或渐变流,曼宁公式有较好的适用性[16]。本文借鉴单一河槽法[17]给出连通水道过流能力的计算方法,对连通水道过流条件进行改写:
| {f1=fA(H)fR(H)−2/3/nf2=fJ(δH) | (2) |
式中,H为本底水位;δH为连通水道与河流及湖泊连接点(Ai和Bi)之间的水位差(ΔH=HAi-HBi)的变化率(δH=ΔH/Δt);n为糙率,可以根据Einstein-Banks方法计算或直接取经验值[17];fA(H)和fR(H)分别为过流断面面积和湿周与随水位变化的函数;fJ(δH)为等效水力坡度随水位变化率及本底水位的取值,与河道与湖泊之间的水位差相关。
本文以计算时段内经连通水道的总水量(由f1·f2计算)与计算时段内湖泊平均容积(V)之间的比值来表征河流与湖泊之间水文连通产生的水体交换量对湖泊的满足程度。因此,f3可表示为:
| f3=βˉV | (3) |
式中,β为比例系数,对于一般计算时段,β=1,对于有“灌江纳苗”或水体置换等需求时段,β<1。
综上,单条连通水道的水文连通度可以表达为:
| HC=TfA(H)5/3fR(H)−2/3√fJ(δH)nˉV | (4) |
河流与湖泊之间的连通水道可能不止一条,各条连通水道对湖泊与河流水文连通的贡献有所差别。连接点与湖泊形心的距离越近,则经连通水道的入湖水流对湖区水动力的改善效果越显著,水体及物质交换效率更高。因此,本文以连通水道与湖泊之间的空间关系设置权重,每条连通水道的权重值表示为:
| wi=R1li | (5) |
式中,li为每条连通水道与湖泊的连接点到湖泊形心的距离;
联合式(4)与式(5),可计算连通水道与湖泊的综合连通度。
| HC1=N∑i=1wiHCi | (6) |
式中,HCt为湖泊与河流的综合水文连通度,HCi为第i条连通水道的水文连通度。在利用式(6)量化河流与湖泊之间水文连通度时,需要获取连通水道与河流、湖泊连接点的水位数据,并根据水位数据的时间间隔来确定计算周期。根据现行建有闸坝河流的调控规则和水位监测频率,推荐以天为计算周期。本文提出的计算模型适用于湖泊出入水源为连通河道的情景,如牛轭湖、人工湖泊等。对于水系复杂的湖泊,即湖泊水位受除连通河道外其他水系的主导,需要对连接点Ai的水位进行率定,确定其他出入水源的贡献。此外,需要确定河流与湖泊间水位差变化对连通水道水流特性的影响,一般需要构建二维水动力模型进行确定。
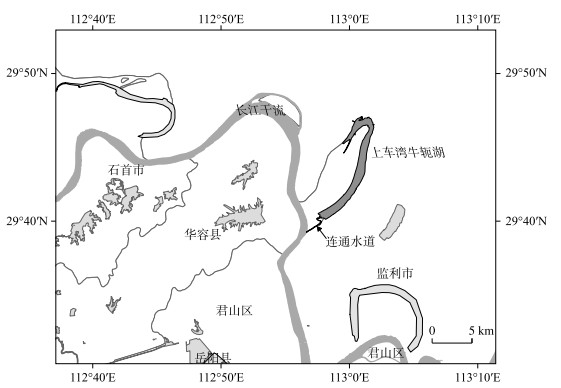
2 模型应用与分析 2.1 研究区域本文以长江中游典型的通江牛轭湖(湖泊)为例,对提出的河湖水文连通量化计算模型进行应用。长江荆江河道独特的水文地质条件形成了我国规模最大的牛轭湖分布区,其中以位于下荆江自然通江的上车湾牛轭湖最为典型[18],如图 2。上车湾牛轭湖生境条件与长江干流有诸多相似性,是众多物种良好的栖息场所,依托该牛轭湖建有长江江豚及中华鲟迁移保护区,是长江生物多样性保护的一个天然基因库,具有重要的现实及潜在生态保护价值。上车湾牛轭湖与长江干流的水文连通是牛轭湖形态、水质变化及生境演变的关键驱动因素。上车湾牛轭湖于1971年实施人工裁弯工程,其上口已经完全淤塞,下口通过长约4 km的连通水道与长江干流自然连通,丰水年基本可全年与长江干流保持连通。
|
图 2 长江中游上车湾牛轭湖地理位置 Fig.2 Geographic location of Shangchewan oxbow lake in the middle reaches of Yangtze River |
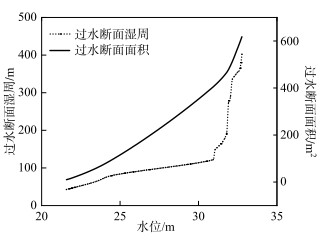
本文基于时间间隔为1 h的水位数据,对2021年湖泊与长江干流水文连通度进行分析,以天为计算周期。2022年实测了湖泊及湖泊与长江干流连通水道的地形资料,湖泊与长江干流连通水道典型断面过水面积及湿周与水位的变化关系见图 3,湿周与水位的变化关系可由分段函数表示,分界点31 m为连通水道漫滩高程。在典型断面的选择上,对于形态均匀的连通水道,一般选取中间部位的断面作为典型断面;对于形态变化显著、深泓起伏较大的连通水道,一般选择最大深泓高程所在的断面为典型断面。连通水道典型断面湿周(fR)和过水面积(fA)与水位的函数关系为:
| fR={8.07H−124.5H<31 m167.1H−5073H⩾ | (7) |
| f_{\mathrm{A}}=18.83 \mathrm{e}^{H / 8.82}-206.6 | (8) |
|
图 3 湖泊与长江连通水道过水断面面积及湿周与水位的关系 Fig.3 Relationship between the cross-sectional area and wetted perimeter of the waterway and the water level |
湖泊与长江干流水体交换的水动力模型基于有限体积法的二维水动力模型,结合地形变化,共设置了99574个三角形有限元网格和50463个节点,湖泊与长江干流连通水道进行了加密处理,选择连通水道与长江干流连接点外沿约200 m处的水位值作为边界条件,模拟区间为2023年5月10日—7月10日。模型由2022年6月与2023年5月实测的湖泊内部及连通水道的水位与流速数据(依托三峡后续工作项目“新水沙条件下荆江故道与长江水系连通修复对策研究”开展)进行验证,流速相对误差在12%以内,水位误差在0.08 m以内,基本可以满足模拟要求。在连通水道中间部位设置断面监控点。
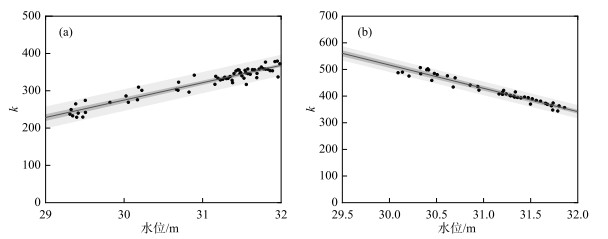
以湖泊与长江连通水道中间断面(距连通水道与长江干流连接点约1.5 km)为统计断面,根据水动力模型的计算输出结果,计算断面水力参数(水深、流速等)。本文建议以日水位变化率(m/d)作为水位变化的计量单位。本节以0.1 m为水位间隔,分析了不同水位级别条件下水体交换流量随水位变化率(δH)的增长率系数(k),见图 4。进一步发现,水体交换流量随水位变化率(δH)的增长率系数(k)与水位之间具有典型的相关性,湖泊与长江干流为单口连通,水体交换的动能基本来自长江干流水位变化形成的势能,因此湖泊内本底水位可直接影响水体交换效率。此外,长江干流水位上升时,长江往湖泊内注入流量(Qin);长江干流水位下降时,湖泊向长江干流输出流量(Qout),这两种水体交换过程对湖泊本底水位的响应关系有所差别。图 4a给出了长江向湖泊注入流量的变化率系数与水位的关系,随着湖泊本底水位的增加,增长率系数k呈线性增加趋势。图 4b给出了湖泊向长江输出流量的变化率系数与水位的关系,随着湖泊本底水位的增加,增长率系数k呈线性降低趋势。值得注意的是,在同等本底水位条件下,湖泊向长江干流输出流量的效率要显著高于长江干流向湖泊注入流量的效率。
|
图 4 长江向湖泊注入流量(a)和湖泊向长江输出流量(b)的变化率系数与水位的关系 Fig.4 Relationship between the rate of change coefficient and water level (a: inflow into the lake, b: outflow from the lake) |
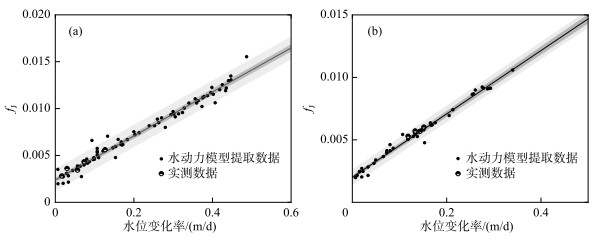
fJ(δH)的取值对式(1)的预测准确度十分重要,长江干流水位变化导致通江口门附近水位在计算周期内处于非恒定状态,且水位变化幅度总体在0.5 m/d以内。本节通过提取水动力模拟获取的断面平均流速值,利用曼宁公式对fJ进行反推,获取模型计算值。通过对比分析,fJ与水位没有显著相关性(相关系数为0.284),与δH呈线性正相关(图 5),且入流及出流情景下,相关关系有所不同,式(9)给出了入流及出流条件下fJ与δH的经验关系式。
| f_{\mathrm{J}}=\left\{\begin{array}{cll} 0.0235 \delta H+0.002 & \text { Inflow } & R^2=0.95 \\ 0.0254 \delta H+0.002 & \text { Outflow } & R^2=0.96 \end{array}\right. | (9) |
|
图 5 长江向湖泊注入流量(a)和湖泊向长江输出流量(b)条件下的水位变化率系数与等效水力坡度fJ的关系 Fig.5 Relationship between the rate of change coefficient and fJ (a: inflow into the lake, b: outflow from the lake) |
由式(9)可以看出,同等水位变化幅度条件下,湖泊向长江输出水流的等效水力坡度会略大,这是由于湖泊靠近上部的水体基本处于静止状态,对入湖的长江水流有明显的顶托作用,导致式(9)中入流的线性增长系数小于出流的线性增长系数,由此可见,对于容积越大、纵深越长的湖泊,其线性增长系数会越小。进一步地,中连通水道与湖泊的连接点至湖泊形心的距离(ri)也是影响fJ与δH变化关系的关键参数,后文将在水文连通度评估中涉及该参数。
基于湖泊与长江连通水道断面特点(fR与fA)以及长江干流水位变化(H与δH),对湖泊与长江干流水体交换强度进行估算,将式(1)~(9)进行整合,估算的湖泊与长江水体交换流量可表达为:
| Q_{\mathrm{e}}=\left\{\begin{array}{l} \left(18.83 \mathrm{e}^{H / 8.82}-206.6\right)^{5 / 3}[(0.0235 \delta H+0.002) / n]\left\{\begin{array}{ll} (8.07 H-124.5)^{-2 / 3} & H<31 \\ (167.1 H-5073)^{-2 / 3} & H \geqslant 31 \end{array}\right. \text { Inflow } \\ \left(18.83 \mathrm{e}^{H / 8.82}-206.6\right)^{5 / 3}[(0.0254 \delta H+0.002) / n]\left\{\begin{array}{ll} (8.07 H-124.5)^{-2 / 3} & H<31 \\ (167.1 H-5073)^{-2 / 3} & H \geqslant 31 \end{array}\right. \text { Outflow } \end{array}\right. | (10) |
式中的经验参数与湖泊形状、容积、与河流连接点空间位置等相关,在使用时,需要实测湖泊与河流连通水道断面参数及水力参数,或运用二维水动力模型确定关键参数。
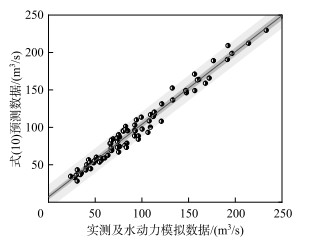
为了分析式(10)对湖泊与长江水体交换的估算效果,本文根据实测数据及二维水动力模型提取的水力参数,对2022年5—6月牛轭湖与长江水体交换流量进行提取,并根据式(10)对水体交换量进行估算。图 6将实测及水动力模拟的水体交换流量与式(10)预测结果进行对比,结果表明:预测整体相对误差为7.2%,基本满足水文连通计算模型需求。
|
图 6 实测及水动力模拟的水体交换流量与式(10)预测结果的对比 Fig.6 Comparison between the measured water exchange flow and the predicted results of equation (10) |
根据实测的湖泊地形数据,利用面/体积分方法,分别给出了湖泊水位与水域面积和水体容积的变化关系,fAl与fVl的拟合关系为:
| f_{\mathrm{Al} }=-8017 H^3+678152 H^2-1.58 H+1.12 \quad R^2=0.99 | (11) |
| f_{\mathrm{Vl} }=28954 H^3-799919 H^2+2 \times 10^6 H+2 \times 10^7 \quad R^2=0.99 | (12) |
联合式(10)与式(4)、(6),以日为计算周期,T=1 d,对2020年全年的水文连通度变化进行计算,HC的计算式可改写为:
| H C_j=\left\{\begin{array}{l} \frac{R_{\mathrm{l} j}}{l_j}\left(18.83 \mathrm{e}^{H_{\rm{J}} / 8.82}-206.6\right)^{5 / 3} \frac{\left(0.0235 {\rm{ \mathsf{ δ}}} H_j+0.002\right)}{n \cdot V_j}\left\{\begin{array}{ll} \left(8.07 H_j-124.5\right)^{-2 / 3} & H_j<31 \\ \left(167.1 H_j-5073\right)^{-2 / 3} & H_j \geqslant 31 \end{array}\right. \text { Inflow } \\ \frac{R_{\mathrm{l} j}}{l_j}\left(18.83 \mathrm{e}^{H_{\rm{J}} / 8.82}-206.6\right)^{5 / 3} \frac{\left(0.0254 {\rm{ \mathsf{ δ}}} H_j+0.002\right)}{n \cdot V_j}\left\{\begin{array}{ll} \left(8.07 H_j-124.5\right)^{-2 / 3} & H<31 \\ \left(167.1 H_j-5073\right)^{-2 / 3} & H \geqslant 31 \end{array}\right. \text { Outflow } \end{array}\right. | (13) |
式中,j为天数,Vj为第j天的湖泊水体容积,Rlj为第j天的湖泊等效半径,lj为第j天的连通水道与湖泊连接点到湖泊形心的距离。
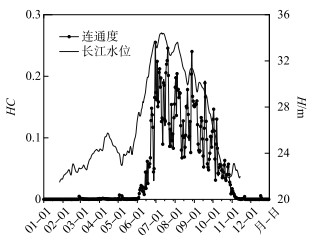
基于式(11)~(13),图 7给出了2020年长江干流水位变化及长江和湖泊间的水文连通度变化。湖泊与长江干流水文连通主要集中在6—11月,且与长江干流水位的变化趋势间存在一定的差异。水文连通度峰值与长江水位变化波峰及波谷的出现频次基本一致,水文连通度主要峰值出现在7月11日、8月8日及9月26日,水文连通度的显著提升均出现在整体上升或下降时间段的变异点。以2020年6月为例,水位基本呈线性增长(增长率为0.25 m/d),水文连通度均值为0.046、最大值为0.165。假设以阶梯上升(以0.5 m/d和0 m/d交替抬升水位)的方式对水位进行调节,水位连通度均值可提升至0.24,最大值可提升至0.81,可有效改善湖泊与长江干流的水文连通度,或许能为面向河湖水文连通的生态调度提供参考。
|
图 7 2020年湖泊与长江水文连通度及水位变化过程 Fig.7 Hydrological connectivity between the lake and the Yangtze River and water level change process in 2020 |
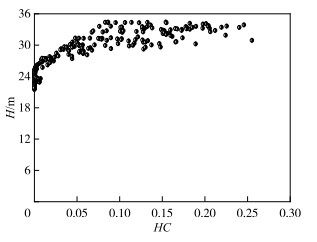
图 8给出了2022年湖泊和长江水文连通度与水位变化的关系,两者的变化关系可以大致分为3个区间:在HC较小时(HC<0.006),与水位基本不相关;在HC处于中间值时(0.006≤HC≤0.08),与水位呈较为显著的正相关关系;在HC为较大值时(HC>0.08), 与水位基本不相关。一方面,长江干流水位变化率与水位的变化关系呈“两头低、中间高”,即水位>31 m与<29 m时,水文变化率较低,因此,HC<0.006和HC>0.08时,HC对水位变化的响应不显著。另一方面,当水位>31 m时,连通水道过流条件(图 3)对水位变化的响应不显著;当水位<29 m时,连通水道过流能力较低,HC对水位变化的响应较弱。
|
图 8 2022年湖泊和长江水文连通度与水位变化的关系 Fig.8 Relationship between hydrological connectivity and water level changes between the lake and the Yangtze River in 2022 |
水文连通是湖泊形态变化[1]与水环境质量改变[19]的关键驱动因素,是湖泊换水周期[20]、水动力变化[3]、水温条件[21]等生境因子的指示因子,同时可作为河湖系统物质交换与生物体输移[2]的指示参数。以往的研究多为定性分析(以是否连通或连通时长为因子),尚未将河湖水文连通度作为量化指标加以分析。本文提出的水文连通度计算方法具有普适性和通用性,可实现对河湖水文连通度的长序列估算,结合历史水质监测数据、遥感影像解译等,可构建湖泊形态与主要水质指标对水文连通度的响应关系。在长江干流苗汛期(6月下旬—7月初)[22],该区间内日均水文连通度在0.2以上,可以引入约5000万尾鱼苗,进而保证湖泊内保护物种(江豚、中华鲟等)适口饵料的供给。湖泊上部水动力条件弱、夏季水华风险较大,通过持续监测与评估可确定水华风险对区间水文连通度均值的响应关系并确定阈值,为湖泊水华预警与治理提供支撑。
针对当前河湖水系连通修复与引调水工程中“实践先于理论”的问题,参照处于健康状态的河湖系统水文连通度,本文提出的计算模型可为水系连通工程的规划与评估提供参考,以科学指导水系连通修复与引调水工程。综上,本文提出的水文连通度计算方法可以在不同时空尺度上加以应用,实现时间尺度上的纵向变化分析以及横向空间尺度上不同河湖系统之间水文连通的对照。
3 结论与建议本文以“通过河流与湖泊之间的连通通道及水文条件,形成的以水流为载体的物质、能量及生物在河流与湖泊之间的传输过程,对河湖系统相对稳定的满足程度”为基本思路,提出了适用于河流与湖泊水文连通的量化计算模型,并以长江中游典型通江牛轭湖为例,对提出的模型进行应用及分析。
本文提出的水文连通度计算模型可以适用于不同类型、与河流有单个或多个连通水道的河湖水文连通,计算的前提是获取连通水道典型断面过流面积及湿周与水位的关系、漫滩阻力特征等,基础参数包括连续水位数据、湖泊湖容与水位的变化关系。
主要结论如下:
1) 本文提出的等效水力坡度与水体交换效率呈线性正相关关系,影响湖泊与河流水体交换的因素为本底水位及水位变化率。同等水位变化幅度条件下,湖泊向河道输出水流的等效水力坡度会略大。随着本底水位的增加,水体交换流量随水位变化率的增长率系数呈线性增加趋势。在同等本底水位条件下,湖泊向河道输出流量的效率要显著高于长江干流向湖泊注入流量的效率。
2) 本文提出的湖泊与长江水体交换流量经验关系式可以很好地估算湖泊与长江水体交换流量(总体相对误差为7.2%)。以2022年上车湾牛轭湖与长江水文连通变化为例,水文连通度峰值一般出现在整体上升或下降时间段的变异点。通过改变水位抬升或下降过程,可有效提升水文连通度均值及峰值。
本文提出的水文连通度计算模型总体较为简便,仅需部分实测数据或者部分时段的水动力模拟即可校准。模型可量化河流与湖泊的水文连通度,可以作为湖泊演变分析、湖泊水环境治理、水生生境修复的基础分析工具,可以为面向湖泊水生态环境改善的生态调度提供量化方案。
在实际应用时,各连接点水位可通过线性或非线性插值方法进行估算,在验证后使用;对于没有实测地形资料的湖泊,可以通过遥感影像估算特点水位下的湖泊面积,采用加权平均方法估算容积。同时,对于有显著季节性特点、特殊时段有水文连通需求(灌江纳苗、水质改善等)的湖泊,可以对特殊时段内日水文连通度赋予更大的权重。
| [1] |
Trigg MA, Michaelides K, Neal JC et al. Surface water connectivity dynamics of a large scale extreme flood. Journal of Hydrology, 2013, 505: 138-149. DOI:10.1016/j.jhydrol.2013.09.035 |
| [2] |
Giblin SM, Houser JN, Sullivan JF et al. Thresholds in the response of free-floating plant abundance to variation in hydraulic connectivity, nutrients, and macrophyte abundance in a large floodplain river. Wetlands, 2014, 34(3): 413-425. DOI:10.1007/s13157-013-0508-8 |
| [3] |
Li YL, Tan ZQ, Zhang Q et al. Refining the concept of hydrological connectivity for large floodplain systems: Framework and implications for eco-environmental assessments. Water Research, 2021, 195: 117005. DOI:10.1016/j.watres.2021.117005 |
| [4] |
Yang S, Wan RR, Li B. Hydrological connectivity research in Lake Taihu Basin: Status, progress and future challenges. J Lake Sci, 2022, 34(4): 1055-1074. [杨素, 万荣荣, 李冰. 太湖流域水文连通性: 现状、研究进展与未来挑战. 湖泊科学, 2022, 34(4): 1055-1074. DOI:10.18307/2022.0402] |
| [5] |
Liu D, Wang X, Li CH et al. Eco-environmental effects of hydrological connectivity on lakes: A review. Resources and Environment in the Yangtze Basin, 2019, 28(7): 1702-1715. [刘丹, 王烜, 李春晖等. 水文连通性对湖泊生态环境影响的研究进展. 长江流域资源与环境, 2019, 28(7): 1702-1715. DOI:10.11870/cjlyzyyhj201907020] |
| [6] |
Liu CM, Li ZL, Wang ZG et al. Key scientific issues and research directions of the interconnected river system network. Acta Geographica Sinica, 2021, 76(3): 505-512. [刘昌明, 李宗礼, 王中根等. 河湖水系连通的关键科学问题与研究方向. 地理学报, 2021, 76(3): 505-512. DOI:10.11821/dlxb202103001] |
| [7] |
Xia JH, Chen YM, Zhou ZY et al. Review of mechanism and quantifying methods of river system connectivity. Advances in Water Science, 2017, 28(5): 780-787. [夏继红, 陈永明, 周子晔等. 河流水系连通性机制及计算方法综述. 水科学进展, 2017, 28(5): 780-787.] |
| [8] |
Gao XP, Hu Z, Yan CD et al. Construction and application of water system connectivity evaluation index system considering hydraulic connectivity. Water Resources Protection, 2022, 38(2): 41-47. [高学平, 胡泽, 闫晨丹等. 考虑水力连通性的水系连通评价指标体系构建与应用. 水资源保护, 2022, 38(2): 41-47. DOI:10.3880/j.issn.1004-6933.2022.02.006] |
| [9] |
Sun C, Chen L, Zhu H et al. New framework for natural-artificial transport paths and hydrological connectivity analysis in an agriculture-intensive catchment. Water Research, 2021, 196: 117015. DOI:10.1016/j.watres.2021.117015 |
| [10] |
Li YF, Xu JY, Wright A et al. Integrating two aspects analysis of hydrological connectivity based on structure and process to support muddy coastal restoration. Ecological Indicators, 2021, 133: 108416. DOI:10.1016/j.ecolind.2021.108416 |
| [11] |
Tockner K, Malard F, Ward JV. An extension of the flood pulse concept. Hydrological Processes, 2000, 14(16/17): 2861-2883. DOI:10.1002/1099-1085(200011/12)14:16/172861:AID-HYP124>3.0.CO;2-F |
| [12] |
Amoros C, Bornette G. Connectivity and bio complexity in waterbodies of riverine floodplains. Freshwater Biology, 2002, 47(4): 761-776. DOI:10.1046/j.1365-2427.2002.00905.x |
| [13] |
Pringle C. What is hydrologic connectivity and why is it ecologically important?. Hydrological Processes, 2003, 17(13): 2685-2689. DOI:10.1002/hyp.5145 |
| [14] |
Western AW, Blöschl G, Grayson RB. Toward capturing hydrologically significant connectivity in spatial patterns. Water Resources Research, 2001, 37(1): 83-97. DOI:10.1029/2000WR900241 |
| [15] |
Xia J, Gao Y, Zuo QT et al. Characteristics of interconnected rivers system and its ecological effects on water environment. Progress in Geography, 2012, 31(1): 26-31. [夏军, 高扬, 左其亭等. 河湖水系连通特征及其利弊. 地理科学进展, 2012, 31(1): 26-31.] |
| [16] |
Yang KJ, Cao SY, Liu XN et al. Comparison of methods for calculating flow capacity of channels with compound cross section. Journal of Hydraulic Engineering, 2005, 36(5): 563-568, 574. [杨克君, 曹叔尤, 刘兴年等. 复式河槽流量计算方法比较与分析. 水利学报, 2005, 36(5): 563-568, 574. DOI:10.3321/j.issn:0559-9350.2005.05.009] |
| [17] |
Yang KJ, Cao SY, Liu XN. Analysis on methods for predicting composite roughness of river channel with compound cross section. Journal of Hydraulic Engineering, 2005, 36(7): 780-786. [杨克君, 曹叔尤, 刘兴年. 复式河槽综合糙率计算方法比较与分析. 水利学报, 2005, 36(7): 780-786. DOI:10.3321/j.issn:0559-9350.2005.07.003] |
| [18] |
Cai XB, Yan RR, Wang XL. Connectivity characteristics and its evolvement trend analysis of old river courses in the lower Jingjiang. Resources and Environment in the Yangtze Basin, 2013, 22(1): 53-58. [蔡晓斌, 燕然然, 王学雷. 下荆江故道通江特性及其演变趋势分析. 长江流域资源与环境, 2013, 22(1): 53-58.] |
| [19] |
Li YL, Zhang Q, Cai YJ et al. Hydrodynamic investigation of surface hydrological connectivity and its effects on the water quality of seasonal lakes: Insights from a complex floodplain setting (Poyang Lake, China). Science of the Total Environment, 2019, 660: 245-259. DOI:10.1016/j.scitotenv.2019.01.015 |
| [20] |
Harvey J, Gomez-Velez J, Schmadel N et al. How hydrologic connectivity regulates water quality in river corridors. JAWRA Journal of the American Water Resources Association, 2019, 55(2): 369-381. DOI:10.1111/1752-1688.12691 |
| [21] |
Tan ZQ, Li YL, Zhang Q et al. Assessing effective hydrological connectivity for floodplains with a framework integrating habitat suitability and sediment suspension behavior. Water Research, 2021, 201: 117253. DOI:10.1016/j.watres.2021.117253 |
| [22] |
Tao JP, Liu HG, Yi R et al. Biological problem and framework construction of biological corridor restoration for river-lake connection in the middle and lower Yangtze River: A case study of Zhangdu Lake. Journal of Hydroecology, 2023, 44(5): 1-8. [陶江平, 刘宏高, 易燃等. 长江中游江湖生物通道恢复的关键生物学问题与框架构建——以武汉市涨渡湖群为例. 水生态学杂志, 2023, 44(5): 1-8. DOI:10.15928/j.1674-3075.202110200362] |
 2024, Vol. 36
2024, Vol. 36 


