(2: 河海大学水科学研究院, 南京 210098)
(3: 河海大学环境学院, 南京 210098)
(2: Insititute of Water Science and Technology, Hohai University, Nanjing 210098, P. R. China)
(3: College of Environment, Hohai University, Nanjing 210098, P. R. China)
太湖是中国长三角地区最重要的水源地,也是中国最大的富营养化湖泊之一,近20年一直受到蓝藻水华暴发的袭扰[1]。水华暴发的必要条件是水柱中有足够的蓝藻生物量[2]以及微囊藻能漂浮在水面上[3]。实际观测发现水华具有快速出现和突然消失的特点,从生物量的来源来说,微囊藻在太湖的平均生长速率约为0.12/d[4],即使以最大的生长速率计算,短时间内由微囊藻原位生长增殖的生物量也很难解释水面上突然出现蓝藻聚集的现象[5]。因此短期内水华在局部湖湾区的突然出现与微囊藻的快速聚集有着内在的联系,这既涉及到微囊藻垂向的上浮,也与微囊藻的水平漂移有关。而微囊藻的水平漂移与风生流水动力输运作用有着极大的关系[6],似乎在一些特定条件下,水动力产生的输运能造成蓝藻的快速聚集,是水华突然暴发的重要机制。
微囊藻是太湖夏季的优势藻种[7],也是太湖水华的主要藻种[8],一般认为微囊藻的质量密度会随光强发生变化[9]并能够进行浮力调节而出现上浮下沉的现象[10]。这种“上浮下沉”现象多在静水状态下室内实验中发现或通过计算静水中微囊藻质量密度变化得到。而实际湖泊中风浪扰动产生水体不歇的运动,其中的紊流扰动会对微囊藻颗粒的“上浮下沉”产生干扰,在风浪较大的情况下风浪会成为干扰微囊藻“上浮下沉”运动的主要影响因素[11]。在一些野外调查中发现,低风速下微囊藻更易于向下风向聚集,能够形成水华[12];而强风速下,风浪的扰动反而会造成漂浮在表面的微囊藻迅速下沉,水华消失[13]。Chen等2023年提出了“适宜风速”的概念,认为对太湖而言,风速在1~2 m/s时微囊藻迁移聚集能力最强[14]。为了解微囊藻的水平聚集与风速的关系,Deng等2016年关注了漂浮在太湖水面上的水华斑块,实测得到在竺山湾水华斑块水平迁移最快的风速是3.6 m/s[15],而梅梁湾水华斑块迁移最快的风速是3.1 m/s[16]。宏观尺度上(cm2),已有相关研究对微囊藻水华斑块的迁移聚集规律进行总结[17]。而更多的情况下,微囊藻是以群体的形态在水中上浮-漂移。但由于微囊藻粒径基本在1000 μm内[18],研究人员难以在湖泊野外调查中直接观测如此微小的颗粒物漂移,因此难以了解微囊藻的运动轨迹和迁移速度。对于理解蓝藻水华“生长—聚集形成水华”[5]中关键的“聚集”过程时,对微囊藻的移动方向、移动速度以及在实际湖泊中的迁移模式、迁移规律的认识仍有欠缺,难以通过现场调查的方法明确影响宏观尺度上微囊藻水华斑块迁移聚集规律的介观(μm)机理。
通过模型的手段可以从介观尺度上研究影响太湖中微囊藻迁移规律的机理,尤其是风生流扰动和光驱动下微囊藻质量密度变化的影响[11]。颗粒在水体中运动的轨迹可以使用IBM方法(individual-based model)进行模拟,这是一个可以考虑颗粒本身性质(质量密度、大小)变化以及紊流对颗粒产生的作用(拖曳及迁移)的方法[19]。使用IBM方法模拟太湖微囊藻的运动轨迹时,可将群体视为独特而离散的实体[20],除模拟紊流运动对群体颗粒的作用及颗粒随流场的迁移之外,还可模拟微囊藻颗粒自身随时间的变化,如质量密度[21]、群体大小[22]、群体形态[23]等,是一种可以研究“生长-聚集形成水华”过程中微囊藻移动方向、移动速度的先进工具。而IBM模拟必须基于最基本的水动力模拟,因为群体的“上浮—下沉”过程必然受到垂向紊流运动的影响,太湖虽然面积/深度比巨大[24],但垂向的动力过程在深度上仍然具有显著的差异[14],因此必须是三维的模型才能支撑IBM模拟。而通过三维水动力预模拟发现,使用矢量和速度稳定的风场与使用接近实际随机矢量和速度的风场得到的流场特征大相径庭,因此使用随机的实际风场才更能反映太湖的流场特征[25]。
为了揭示实际太湖中微囊藻的移动方向、移动以及迁移模式、迁移规律,本研究基于实际的风场对水动力进行了三维模拟,作为IBM模型的水动力背景,同时开发了包含微囊藻质量密度随光照发生变化的计算模块、微囊藻颗粒在垂向紊动中的受力计算模块的IBM模型,模拟了光照和风场变化情况下微囊藻颗粒在水中的运动轨迹,进一步探讨了风场对微囊藻颗粒的迁移速度和方向、水平迁移的模式以及微囊藻水华形成的影响。
1 材料与方法 1.1 计算模型与数据来源计算模型包含太湖,并将22条[24]入湖河流作为流量、通量边界进行考虑(图 1)。水动力及相关计算所需要的数据包括:(1)2017年逐月太湖出入湖水量、逐日水位变化、逐日降雨量;(2)2011—2020年太湖逐小时风速、风向;(3)太湖的湖底高程;(4)基于卫星数据分析的太湖水华暴发区域,这些数据参考了太湖流域水资源保护局、中国气象科学数据共享平台无锡站和国家科技基础条件平台(国家地球系统科学数据中心-湖泊-流域分中心)的数据。水质、微囊藻生物量、微囊藻颗粒大小以及太湖分层流场数据来自研究小组在太湖的现场监测和调查[14]。使用ADCP调查水动力的方法以及微囊藻的采集方式详见附录。
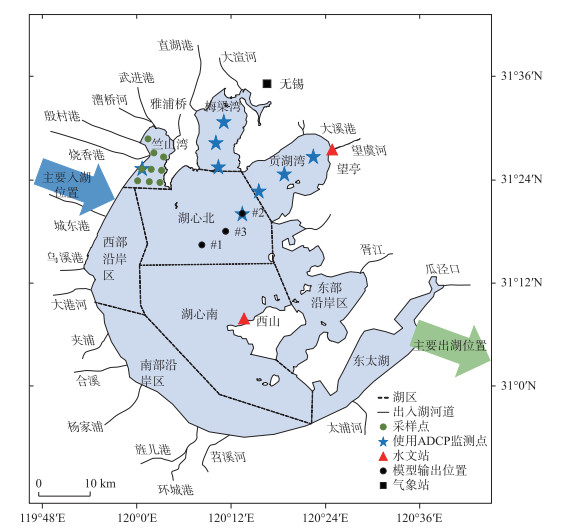
|
图 1 研究区域和监测站位置 Fig.1 Location of the study area and monitoring stations |
本研究建立的微囊藻迁移IBM模型包括三维水动力计算模块、微囊藻颗粒在垂向紊动中的受力计算模块和微囊藻质量密度随光照发生变化的计算模块(图 2)。三维水动力计算模块在模拟太湖流场时使用σ坐标,垂向分为10层[26],在实际的风场下输出太湖流场数据作为水动力背景[27]。下文为了叙述方便,以表层、中层和底层的网格分别代表表面(第10层)、中层(第5层)和底层(第1层)。微囊藻质量密度变化模块模拟微囊藻的质量密度随光强的变化[28]。模型中各个位置的光强不仅随时间变化,也随水深变化[29]。微囊藻质量密度变化模块根据微囊藻此刻所在位置的光强,输出微囊藻不同时刻的质量密度。微囊藻颗粒在垂向紊动中的受力计算模块根据水动力计算模块输出的动力学计算结果和质量密度计算模块输出的微囊藻质量密度在Matlab中对微囊藻颗粒进行受力计算,使用非均匀速度场中球体的确定性运动方程(简化M-R方程)来模拟微囊藻的运动[30],IBM模型最终输出微囊藻颗粒在太湖水体中随流场的迁移轨迹。微囊藻颗粒迁移的IBM模型及各模块的构建详见附录。
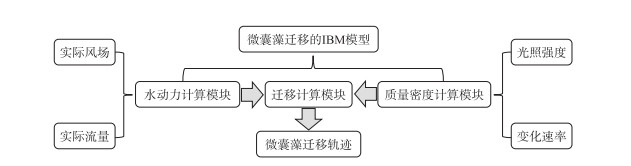
|
图 2 微囊藻迁移的IBM模型结构 Fig.2 Diagram of the structure for IBM of Microcystis movement |
本研究使用太湖实测的水文、蓝藻数据对IBM模型中的水动力计算模块、迁移计算模块进行率定和验证,质量密度计算模块中的微囊藻质量密度随光强变化速率参照之前的研究[28]进行计算。
太湖三维水动力计算模块先参照相关研究进行初始参数设定[26],然后使用2017年太湖的水文数据反复试算[27]。通过2017年太湖西山、望亭水文站的水位数据以及2017年太湖内8个测点的紊流动能数据对太湖三维水动力子模型进行验证(图 1),使用纳什系数作为评价指标。结果表明,2个水文站的水位实测数据与模拟数据的纳什系数大于0.80,8个测点的紊流动能实测数据与模拟数据的纳什系数大于0.50。因此,本研究建立的三维水动力子模型对2017年太湖水位、紊流的模拟具有一定的合理性。
微囊藻迁移计算模块对2017年8月28—29日以及9月13—14日微囊藻在太湖的运动进行模拟。2017年8月28—29日太湖竺山湾中偏北的测点在8月29日测得的微囊藻中值粒径(d50)比前一天减小,偏南的测点在8月29日测得的微囊藻d50比前一天增加(图 1)。实测数据说明8月28—29日大粒径的微囊藻向南移动[14],模拟结果反演了该时间段内微囊藻的迁移方向和距离。基于卫星数据分析太湖水华面积由9月13日的132 km2下降至9月14日的33 km2。实测数据说明9月13—14日水华消失,模拟结果反演了该时间段内水华消失是由于微囊藻的水平迁移和下沉。并采用结构相似性指标(SSIM)对实际水华面积变化的卫星图片和IBM模型反演水华面积变化的图片进行评价,按照模型网格划分对图片进行分块处理,分别计算各分块实际和反演水华面积图形的结构相似性[31],最后进行汇总。结果表明,反演的SSIM为0.19,达到准确性要求。因此,可以认为本研究建立的微囊藻迁移IBM模型对微囊藻在太湖内的迁移模拟是合理的。
本研究对以上时间段微囊藻迁移反演的模拟与实测数据对比,以及水位、紊流动能的模拟与实测的对比详见附录。
1.3 模拟内容本研究选择3种太湖微囊藻的常见粒径[18],在验证后的微囊藻迁移IBM模型中模拟群体从不同位置出发在太湖内的运动(表 1)。基于卫星数据分析2017年5月22—26日太湖水华面积变化表明,5天内太湖水华面积增加了633 km2,水华的边界扩张了约30 km。5月22日,水华只局限在西部沿岸区,5月16日除东部沿岸区(无信号)、东太湖(无信号)外,全太湖基本都有水华(图 3)。因此,可以认为这段时间太湖流场适宜微囊藻水平迁移。IBM模型中的水动力背景是验证后太湖三维水动力子模型输出的2017年5月22—26日的流场。IBM模型中对微囊藻质量密度变化的模拟基于微囊藻质量密度子模型,根据太湖实测的结果,微囊藻的初始质量密度设置为980 kg/m3[32],水面最大的光照强度设置为2000 μmol/(m2·s)[29]。
| 表 1 模拟内容 Tab. 1 Simulation cases |
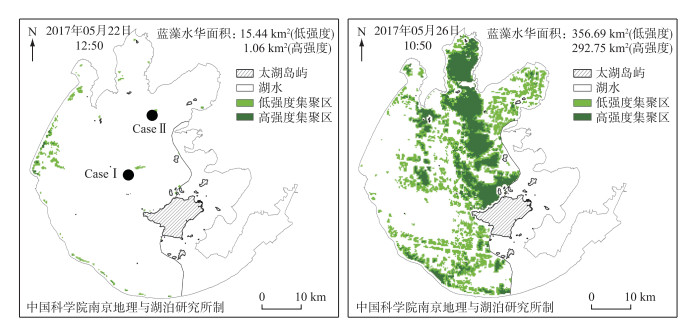
|
图 3 模拟期间太湖水华面积变化过程 Fig.3 Changes of water bloom area in Lake Taihu during the simulation |
CaseⅠ和Case Ⅱ模拟了不同粒径的微囊藻从湖心和5月26日水华暴发区域中心位置出发的轨迹,探究微囊藻水平迁移的规律。
2 结果 2.1 模拟期间的风场和流场将模拟时段内的水文气象数据绘制于图 4。由图 4a可见,模拟时段内的风向比较紊乱。从日均风速变化来看,5月22—26日的风速逐渐下降,5月22日日均风速最大(3.48 m/s),5月25日和26日的日均风速比较小(分别为1.64和1.93 m/s)。
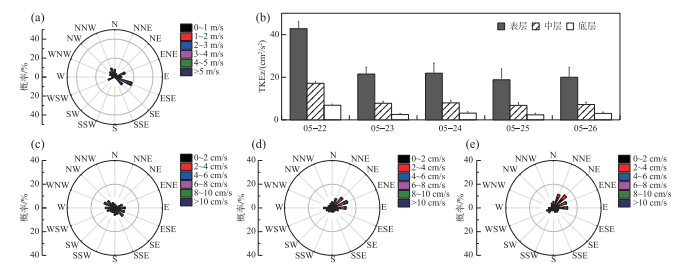
|
图 4 模拟时段内的风场和流场(a为模拟期间风场玫瑰图;b为#3的逐日TKEz;c为#3的表层流场玫瑰图;d为#3的中层流场玫瑰图;e为#3的底层流场玫瑰图) Fig.4 Wind fields and flow fields during the simulation period: (a) wind rose, (b) daily TKEz in #3, (c) surface flow rose in #3, (d) middle flow rose in #3, (e) bottom flow rose in #3 |
垂向紊流动能(TKEz)直接影响微囊藻的上浮、下沉[26]。由图 4b可见,模拟时段内日均TKEz的变化趋势也与风速变化趋势一致,5月22日最大(表层42.77 cm2/s2),5月25日和26日TKEz比较小(表层分别为18.82和20.01 cm2/s2)。TKEz存在明显的垂向衰减,衰减的比例与风速变化关系不大,表层平均是中层的2.7倍,是底层的7.3倍。
由图 4c~e可见,模拟时段内表层的流向与风向一样,比较紊乱,中层和底层有比较稳定、向东的流动。对流速大小垂向差异的分析表明,表层流速是中层的3.9倍,是底层的8.7倍,这个衰减比例也与风速变化关系不大。
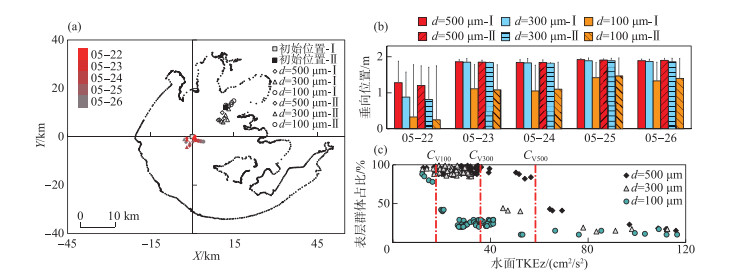
2.2 微囊藻在太湖中迁移的模拟 2.2.1 迁移轨迹以典型群体为代表分析微囊藻在太湖中的迁移,典型群体是模拟时间段内总轨迹长度为该粒径所有群体中位数的群体,对微囊藻迁移过程中的指标分析绘制于图 5。图 5a为典型群体逐日的起始位置和最终位置,图 5b为不同粒径群体逐日的平均垂向位置和标准差,图 5c为每2 h统计的水面TKEz与漂浮在水面(距水面 < 0.2 m)群体的占比。
|
图 5 模拟微囊藻运动的分析(a为典型群体每天的水平轨迹;b为不同典型群体每天的平均垂向位置;c为表层群体占比与水面TKEz的关系) Fig.5 Microcystis migration process: (a) daily initial and final positions of typical colonies, (b) daily average vertical positions and standard deviations of typical colonies, (c) proportion of surface TKEz to the percentage of colonies floating at the surface |
由图 5a可见,5月22—26日,总体来说无论从哪个位置出发,粒径较大的群体都向西移动,小粒径群体(d=100 μm)向东移动。从日迁移距离来看,粒径较大的群体迁移距离较长,小粒径群体迁移距离较短。
由图 5b可见,5月22日以后,由于风速下降,粒径较大的群体基本都能维持在水柱上层(距水面 < 0.4 m)移动,小粒径群体基本在水柱中下层移动。
由图 5c可见,当水面TKEz达到某一临界值时,各粒径微囊藻在水柱上层的占比会急剧下降。小粒径群体的TKEz临界值约为10 cm2/s2,中等粒径群体(d=300 μm)的TKEz临界值约为33 cm2/s2,大粒径群体(d=500 μm)的TKEz临界值约为50 cm2/s2。
2.2.2 水平迁移速度(1) 速度大小
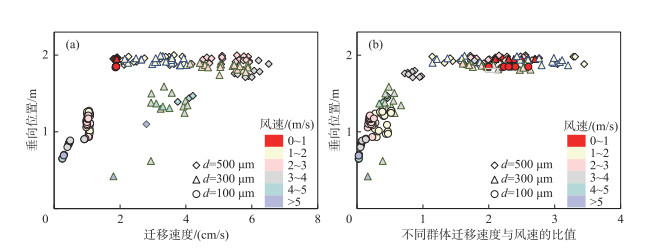
将模拟时间段内各粒径微囊藻典型群体的水平迁移速度大小的分析结果绘制于图 6。图 6a为每2 h统计的群体水平迁移速度大小与垂向位置的关系,图 6b为每2 h统计的群体水平迁移速度大小与此时风速的比值与垂向位置的关系。
|
图 6 不同群体水平迁移速度(a为不同群体迁移速度与垂向位置的关系,b为不同群体迁移速度与风速的比值与垂向位置的关系) Fig.6 Analysis of Microcystis colony horizontal migration velocity: (a) relationship between horizontal migration velocity magnitude and vertical position, (b) ratio of horizontal migration velocity magnitude to wind speed and vertical position |
由图 6a可见,微囊藻水平迁移速度大小与垂向位置有关,越接近水面,水平迁移速度越快。相同风速下,垂向位置相近的群体,无论粒径大小,水平迁移速度均相近。随风速增加,水面的微囊藻水平迁移速度也增加。
由图 6b可见,微囊藻水平迁移速度与风速的比值也与垂向位置有关,越接近水面,比值越大。微囊藻漂浮在水面时(距水面 < 0.2 m),比值约为2%,微囊藻在水柱中下层时(距水面>1 m),比值约为0.3%。比值的大小与风速关系不大,即使风速增加,只要微囊藻漂浮在水面,依旧可以维持较高的比值。
(2) 速度方向
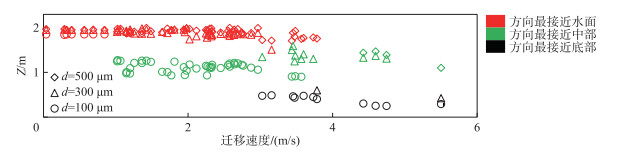
每2 h统计群体水平迁移速度方向与所在表、中、底3层流向之间的夹角,通过夹角的绝对值大小判断微囊藻迁移方向与流向的相似程度。将模拟时间段内各粒径微囊藻典型群体的迁移方向与流向的相似程度和垂向位置的关系绘制于图 7。
|
图 7 不同群体水平迁移速度方向 Fig.7 Similarity of horizontal migration velocity direction to the flow direction |
由图 7可见,无论粒径大小,微囊藻的水平迁移方向都与所在水层的流向相似。当微囊藻能漂浮在水面时,其水平迁移方向接近表层的流向,随着微囊藻下沉,其水平迁移方向也向对应水层的流向转变。
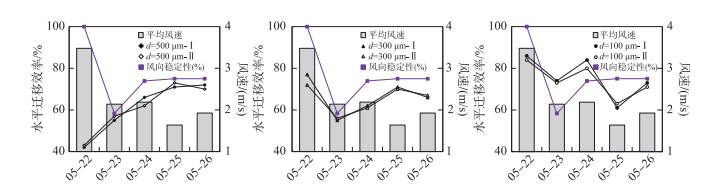
2.2.3 水平迁移效率水平迁移效率为逐日微囊藻迁移距离(最终位置与初始位置之间的直线距离)与微囊藻轨迹长度之间的比值。风向稳定性为每天风向在该日盛行风向±45°之内的时间比。将模拟时间段内不同粒径微囊藻水平迁移效率的平均值与该日平均风速、风向稳定性绘制于图 8。总体来说小粒径群体迁移的轨迹长度虽然短,但是水平迁移效率反而更高,模拟时间段内平均为75%,中大粒径的群体水平迁移效率平均值在60%左右(图 8)。从不同粒径群体的水平迁移效率与该日风场的关系来看,风向稳定和风速可以使微囊藻较稳定地停留在某一水层这两个条件同时满足时,水平迁移效率较大。如5月22日风速较大,中小粒径的微囊藻基本在水柱中下层(图 5b),风向也很稳定,此时中小粒径群体的水平迁移效率是模拟时间段内的最大值。5月25—26日风速较小(< 2 m/s),中大粒径的微囊藻基本在水柱中上层(图 5b),风向也很稳定,此时中大粒径群体的水平迁移效率较高。两个条件有一个不满足都会造成水平迁移效率下降。如5月23日尽管风速较小,大粒径群体基本在水柱上层(图 5b),但是由于风向不稳定,大粒径群体的水平迁移效率也较小。
|
图 8 水平迁移效率与风场的关系 Fig.8 Relationship between the migration efficiency and wind fields |
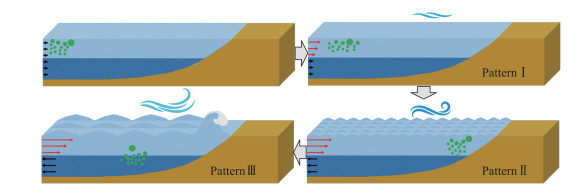
综合微囊藻水平迁移的速度大小和速度方向,微囊藻在太湖中有3种水平迁移模式(图 9)。Pattern Ⅰ为表层慢速迁移,此类迁移的特征是迁移速度小、迁移方向与表层流向一致。Pattern Ⅱ为表层快速迁移,此类迁移的特征是迁移速度大、迁移方向与表层流向一致。Pattern Ⅲ为中下层慢速迁移,此类迁移的特征是迁移速度小、迁移方向与中下层流向一致。以大粒径群体为例,Pattern Ⅰ变为Pattern Ⅱ的风速阈值是2 m/s,Pattern Ⅱ变为Pattern Ⅲ的风速阈值是4 m/s。其他粒径群体也有相似的特点,但是Pattern Ⅱ变为Pattern Ⅲ的风速阈值更低。
|
图 9 微囊藻的水平迁移模式 Fig.9 Horizontal migration patterns of Microcystis |
在对水华斑块的现场调查中,研究者在太湖竺山湾发现[15],风速低于3.6 m/s时,水华斑块的迁移速度与风速呈正相关。风速大于3.6 m/s时,水面就难以形成水华斑块。在对微囊藻迁移通量的现场调查中,研究者在太湖竺山湾发现[14],风速在2~3 m/s之间时,66%以上的微囊藻生物量集中在距水面1 cm的水层,随水流快速移动,在太湖梅梁湾也有相似的发现[16]。这是本文在介观尺度上总结的微囊藻水平迁移模式变化在宏观尺度上的表现。风速较小时,微囊藻聚集在水面,出现Pattern Ⅰ和Pattern Ⅱ的水平迁移模式。若风速进一步增加,微囊藻基本在水柱中下层,出现Pattern Ⅲ的水平迁移模式。由于微囊藻抵抗风浪扰动的能力与粒径呈正相关[11],因此Pattern Ⅱ变为Pattern Ⅲ的风速阈值也与粒径呈正相关。
综上,介观尺度上微囊藻有3种水平迁移模式,在宏观尺度上表现出的就是水华斑块迁移速度随风速的变化和微囊藻迁移通量的垂向差异。
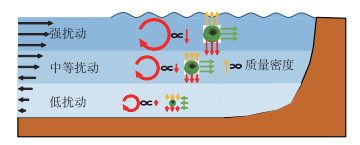
3.2 微囊藻水平迁移模式的影响因素太湖属于浅水湖泊,水面的水流运动主要受风的驱动,中部的水流运动主要受水的粘度、水位和风场变化引起的压力梯度力驱动,底部的水流运动主要受压力梯度力和底部摩擦力驱动[25]。从水面至水底不仅流速衰减[33],流向也会存在切变[34]。本研究对太湖分层流场的分析(图 4c~e)以及太湖流场的实测都表明[14],太湖表层流速是中层的4倍左右,是底层的8倍左右。表层流向与风向相似[35],中、底层流向与表层流向相反[36]。在水平方向上微囊藻的主要受力是紊流拖曳力,它会使得微囊藻的迁移逐渐接近所在位置水的流动[30]。因此,风扰动下的微囊藻垂向分布决定它的水平迁移(图 10)。
|
图 10 垂向位置对微囊藻水平迁移影响示意 Fig.10 The influence of vertical position on the horizontal migration of Microcystis |
从微囊藻水平迁移的速度大小来看,由于浅水湖泊中的表层直接受风驱动,是快速流动的水层[37]。因此,相同风速下,微囊藻距水面越近,速度越快。随风速增加,如果微囊藻仍能克服风浪扰动停留在水面,其迁移速度也会增加。如果微囊藻难以克服风浪扰动而下沉,其迁移速度和流速一样,会出现相似的垂向衰减现象(图 6a)。从微囊藻水平迁移的速度方向来看,其与所在水层的流向最接近(图 7a)。由于太湖的盛行风向和吞吐流流向相反,风生流的反向流加强了吞吐流,因此太湖流向的垂向切变比较明显[36]。当不同粒径的微囊藻所在水层不一致时,其迁移方向也会存在较大差异(图 5a)。
实际情况下太湖风场是连续变化的,微囊藻的垂向分布也可能发生变化,其水平迁移模式会对风速变化产生不同的响应。当风速极小或无风时,虽然占主导地位的吞吐流会驱使聚集在水面的微囊藻向下游迁移,但是由于太湖极低的吞吐流流速[38],微囊藻基本会停留在原位。当风速较小时,微囊藻仍聚集在水面,此时微囊藻的迁移速度虽然接近表层流速,迁移方向与表层流向一致,但是由于风速较低,表层流速也很低,出现Pattern Ⅰ的水平迁移模式。随着风速升高,表层流速也升高,此时虽然一些较小的微囊藻会下沉,但是仍能停留在水面的中大粒径群体会以较快的速度随表层水迁移,出现Pattern Ⅱ的水平迁移模式。使得微囊藻出现Pattern Ⅱ迁移模式的风速就是“适宜风速”,在这种迁移模式下,微囊藻可以在水面快速迁移聚集,增加了水华暴发的风险。对太湖竺山湾相同微囊藻生物量在不同风速下形成水华的时间研究表明,“适宜风速”(2.6 m/s)下形成水华的时间只需要其他风速(1 m/s或者4 m/s)下的一半左右[14]。当风速进一步增加并超过了大多数微囊藻的“临界风速”时,微囊藻基本在水柱中下层,迁移速度反而由于流速的垂向衰减而下降,迁移方向也更接近中下层的流向,出现Pattern Ⅲ的水平迁移模式。在太湖,这往往意味着微囊藻迁移方向与表层流向相反。
在深水湖泊中,由水温分层引起的温度/密度流也会改变藻的垂向分布,进而影响到藻的水平迁移模式,在伊利湖[39]、加利利湖[40]建立的水华预测模型中都有相应的研究。而由于太湖没有显著的水温分层[41],本研究未考虑水温的影响。此外,对于微囊藻大小、结构、太湖营养盐等因素的影响也有待进一步研究。
综上,风扰动下的微囊藻垂向分布决定了它的水平迁移。微囊藻越接近水面,水平迁移速度越快,其水平迁移的速度方向与所在水层的流向接近。3种水平迁移模式中,Pattern Ⅱ(表层快速迁移)容易造成水华的暴发。
3.3 微囊藻水平迁移对太湖水华面积变化的影响微囊藻的水平迁移对于太湖水华的暴发是必要的过程,但这可能是一个缓慢而长期的过程。太湖水华的暴发,尤其是水华面积的突然增加,主要是由风速下降引起微囊藻上浮造成的,而不是短时间内其他区域微囊藻的快速聚集。首先,微囊藻的迁移轨迹长度是有限的。微囊藻在太湖中迁移速度的最大值很难超过当时的水面流速。而对太湖水面流速的模拟和实测[14]都表明,太湖水面流速最大约为风速的2%,并且当风速增加到4 m/s以上时,太湖水面流速与风速的比值还会下降,这可能是由于风速增加、波浪加强改变了水面的粗糙度[42]。从不同群体迁移速度与风速的比值来看,当微囊藻漂浮在水面时,迁移速度也会接近风速的2%左右,而一旦微囊藻下沉,这个比值会迅速下降到1%以下(图 6b)。太湖夏季的平均风速是2.37 m/s[24],即使以最大的比值计算迁移速度,微囊藻夏季每周平均的迁移轨迹长度也只有28 km。微囊藻在水面形成较小的水华斑块后,由于风可以直接驱动水华斑块,迁移能力有一定的提高,最大也只能达到风速的4%左右[15]。而风速增加虽然能提高微囊藻迁移速度,但是也会造成微囊藻下沉,降低微囊藻迁移的速度(图 6a)。太湖南北长约60 km,东西宽约45 km,1 d以内微囊藻在太湖中的迁移范围是有限的。
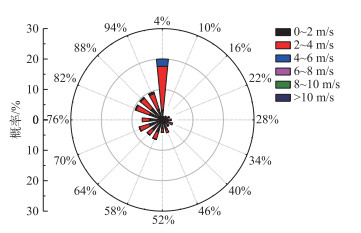
其次,微囊藻迁移的轨迹长度转化为迁移距离的水平迁移效率也是有限的。大粒径微囊藻基本漂浮在水面,且风向比较稳定的情况下(5月25—26日),水平迁移效率也只有70%左右(图 8a)。当风向不稳定或者风速变化造成微囊藻在水柱中浮沉时(5月22日),水平迁移效率下降到了42%。小粒径群体虽然基本在水柱中下层,其水平迁移效率却超过60%(图 8c)。但是由于其迁移轨迹长度很小,最终的迁移距离也很短。这主要是因为太湖风生流的反向流加强了吞吐流,中底层流向反而相对稳定(图 4d~e)。提高水平迁移效率需要微囊藻迁移方向稳定,而微囊藻迁移方向与所在水层流向相近,太湖的流向又存在垂向改变。因此,更高的水平迁移效率需要稳定且较弱的风场(微囊藻可以漂浮在水面,风速 < 2 m/s)或者稳定且很强的风场(微囊藻难以漂浮在水面,风速>4 m/s)。当出现稳定且较弱的风场时,如水面本就存在水华斑块,可能会驱使水华斑块向下风向集中,形成面积较小、生物量更高、维持时间更长的“厚层水华”[43]。对太湖流域2011—2020年逐小时风场进行分析,满足这个条件的风场只占总时间的18.6%(图 11)。因此,太湖多变的风场使得微囊藻水平迁移效率很难增加,也限制了微囊藻水平聚集的能力。
|
图 11 2011—2020年太湖流域风场特征 Fig.11 Characteristics of wind field in Lake Taihu from 2011 to 2020 |
微囊藻的水平迁移对太湖水华的短期时效性虽然缓慢,但却具有长期的累积性。从多年来太湖夏季水华暴发时的卫星照片分析发现,太湖夏季水华易暴发的区域为太湖北部的竺山湾和梅梁湾附近[44]。野外调查中,夏季在太湖西北部的竺山湾[14]、梅梁湾[15]都观察到了微囊藻的净输入。分析其原因是微囊藻对风速的动态响应所形成的水平迁移模式会产生一种长期的“水平迁移累积”。太湖夏季的盛行风是东南风,平均风速是2.37 m/s,太湖夏季的微囊藻粒径在500 μm左右[18],太湖湖心的藻密度近年来最高约为0.8×108 cells/L[45]。在这样的风场下,湖心区的微囊藻生物量尽管很难在原位形成水华,但在风速较低时,湖心的微囊藻会以Pattern Ⅰ或Pattern Ⅱ的模式向西北湖区漂移。风速增加到迁移模式转变为Pattern Ⅲ时,尽管微囊藻在中下水层中受吞吐流和风生流反向流的影响离开西北湖区,但是迁移速度较慢,且当风速下降,又会上浮、较快地返回。因此,总体上形成夏季微囊藻向西北湖区漂移快,从西北湖湾向外迁移慢的现象,快与慢之间的差值形成“水平迁移累积”,这是造成西北湖区微囊藻生物量高的重要机制。由于西北湖区是太湖主要入湖湖区,受入湖水质的影响,水质较差,微囊藻生长率本身较高[46],这也会造成西北湖区的微囊藻生物量在原位生长和外来输入的影响下持续上升,产生恶性循环。
对太湖梅梁湾微囊藻原位生长率的研究也表明[4],尽管近岸区的微囊藻原位生长率更高,但不足以解释巨大的微囊藻生物量差异。因此,盛行风下微囊藻“水平迁移累积”是至关重要的。到秋、冬季节,太湖的盛行风向向北偏移,此时营养盐水平更高的太湖梅梁湾微囊藻原位生长率已为负数[4],营养盐水平更低的南部沿岸区却开始出现水华[47],这可能与微囊藻向下风向的南部湖湾区产生的“水平迁移累积”有关。
4 结论1) 由于风扰动下的垂向变化,介观尺度上微囊藻会出现3种水平迁移模式,在宏观尺度上表现出的就是水华斑块迁移速度随风速的变化和微囊藻迁移通量的垂向差异。以大粒径群体为例,Pattern Ⅰ变为Pattern Ⅱ的风速阈值是2 m/s,Pattern Ⅱ变为Pattern Ⅲ的风速阈值是4 m/s。其他粒径群体也有相似的特点,但是Pattern Ⅱ变为Pattern Ⅲ的风速阈值更低。
2) 风扰动下的微囊藻垂向分布决定了它的水平迁移。微囊藻越接近水面水平迁移速度越快,其微囊藻水平迁移的速度方向与所在水层的流向接近。3种水平迁移模式中,Pattern Ⅱ(表层快速迁移)容易造成水华暴发。
3) 微囊藻的水平迁移对太湖水华的影响是缓慢、长期的。微囊藻对风速的动态响应所形成的水平迁移模式产生了一种长期的“水平迁移累积”,也就是微囊藻向下风向湖湾迁移的快,从湖湾向外迁移的慢,因而产生长期在下风向湖湾部聚集的效应。
5 附录附录见电子版(DOI: 10.18307/2024.0613)。
附录 1 使用ADCP记录流场的方法以及微囊藻的采集方式为了了解太湖的水动力特征和微囊藻的生理特征,作者所在课题组于2017年不同月份在太湖中7个采样点使用声学多普勒流速仪(ADCP)记录了3个方向分层流场的数据,于2017年8月24日—2017年8月30日在太湖竺山湾内进行了连续采样,采集3个方向分层流场的数据以及微囊藻的样品(图1)。不同采样点的经纬度、采样种类以及采样时间见附表Ⅰ。
| 附表 Ⅰ 太湖采样点经纬度 |
在太湖中7个采样点使用ADCP记录3个方向分层流场的数据时,先乘采样船通过GPS定位到达设定的点位,将ADCP固定在采样船上测定各点位不同水深的三维流速值,每次监测30 min,测量间隔时间为2s。声学多普勒流速仪自身仪器高度为0.27 m,从水面0.27 m向下至水底,每隔0.13 m自动采集流速数据(附图Ⅰ)。

|
附图 Ⅰ 固定在采样船上的声学多普勒流速仪 |
由于ADCP受仪器自身高度的影响,对流速的采集存在盲区,尤其是表面的流速很难被采集到。为了准确的了解不同风速下太湖3个方向流速的垂向变化,尤其是水体表层的流速,作者所在的课题组在太湖竺山湾进行了连续6天的野外观测。为了测量表面的流速,将ADCP倒置安放湖底表面,通过调整三角架支柱的埋深,使得探头刚好能够监测到水体表层0~0.13 m的平均三维流速。流场的监测指标为每隔1 s采集自表面往下每隔0.13 m的水层流场数据(附图Ⅱ)。

|
附图 Ⅱ 太湖竺山湾内的观测平台和声学多普勒流速仪 |
2017年8月24日—29日,作者所在课题组在太湖竺山湾内设置了9个采样点采集太湖竺山湾的微囊藻样品。在每个采样点位,有机玻璃便携式采水器采集水下0、0.5、1.0、1.5和2.0 m的水样各5 L,分别用63 μm浮游植物网浓缩,并冲洗2次后装入50 mL样品瓶。后续在实验室内分析太湖微囊藻的群体粒径和群体质量密度。
2 微囊藻迁移的IBM模型及各子模型的构建 2.1 主模型本研究从受力分析的角度出发,在Matlab 2018a平台上,使用迭代法,建立微囊藻迁移IBM模型。首先分析此刻微囊藻群体在紊流中所受的外力,并根据各个方向上的外力计算各个方向上的加速度。然后,根据此刻微囊藻群体所在的位置和速度,计算出这个时间步长结束后微囊藻群体的位置和速度。在下个时间步长内进行同样的计算,直至计算时间结束。
本研究建立的微囊藻迁移IBM模型在结构上分为主模型、水动力子模型和微囊藻质量密度子模型。对紊流中的微囊藻群体受力分析可以发现,微囊藻群体所受的外力有3种,第1种是紊流对微囊藻群体的拖曳力,第2种是重力,第3种是浮力。在主模型中,对以上3种外力进行矢量相加,求出各个方向上的加速度,最后根据这一时刻的加速度和上一时刻的位置与速度计算下个时刻的位置与速度。在计算紊流对微囊藻群体的拖曳力时,使用非均匀速度场中球体的确定性运动方程,由水动力子模型输出此时刻的非均匀速度场。在计算重力和浮力对微囊藻群体的作用时,由微囊藻质量密度子模型输出此时刻微囊藻群体的质量密度。
在本研究中,我们使用Matlab 2018a建立了微囊藻迁移IBM模型的主模型,以正东、正北和垂直水面向上作为x、y、z的正方向。各个方向上控制微囊藻运动的方程为:
| xn=xn−1+Sx | (S1) |
| yn=yn−1+Sy | (S2) |
| zn=zn−1+Sz | (S3) |
| Sx=un−1×Δt | (S4) |
| Sy=vn−1×Δt | (S5) |
| Sx=wn−1×Δt | (S6) |
式中,
根据每个时间步长内的加速度,计算出这个时间步长结束后的速度,根据以上的控制方程,计算微囊藻群体在下一步开始时的位置。微囊藻群体的加速度计算公式如下:
| un=un−1+axn−1×Δt | (S7) |
| vn=vn−1+ayn−1×Δt | (S8) |
| wn=wn−1+azn−1×Δt | (S9) |
| →an=→Fhnm | (S10) |
式中,
根据各个时刻微囊藻群体所受的外力,计算这个时刻微囊藻的加速度,根据以上方程,计算微囊藻群体在下一步开始时的速度。微囊藻在同一时刻所受的外力有紊流拖曳力、浮力和重力,这三种外力的矢量和为微囊藻群体所受外力的合力。微囊藻群体所受外力的计算公式如下:
| →Fhn=→Fwn+→fn+→Gn | (S11) |
| →Fwn=→Fwnx+→Fwny+→Fwnz | (S12) |
| Fwnx=(3μCDRed4ρpd2p(un−uwn)+12(ρρp)2uwn∂uwn∂xddt(un−uwn))×m | (S13) |
| Fwny=(3μCDRed4ρpd2p(vn−vwn)+12(ρρp)2vwn∂vwn∂xddt(vn−vwn))×m | (S14) |
| Fwnz=(3μCDRed4ρpd2p(wn−wwn)+12(ρρp)2wwn∂wwn∂xddt(wn−wwn))×m | (S15) |
| fn=ρgmρp | (S16) |
| Gn=mg | (S17) |
式中,
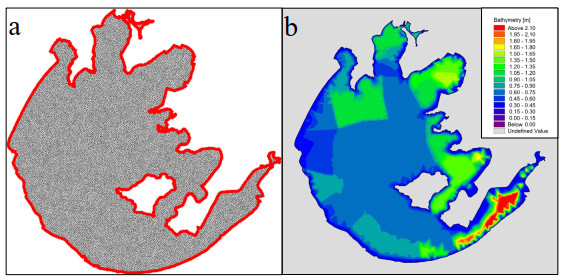
本研究建立的三维水动力子模型包括太湖湖面及22条主要出入湖河道(图1),面积2338 km2,为了更好的模拟地形变化和风生流造成的垂向紊动,垂向采用σ坐标,均分为10层。经纬度坐标系选取WGS84坐标系,投影带坐标系选取北京1954坐标系,中央经线为120°E。模拟区域在水平上划分为19885个三角形网格(附图Ⅲa),未进行局部加密,网格大小范围为0.08~0.14 km2。模拟区域的湖底高程根据太湖流域管理局提供的湖内点位数据进行插值,以湖底最低位置的高程为0(附图Ⅲb)。
|
附图 Ⅲ 太湖三维水动力子模型网格划分及湖底高程(a.网格划分;b.湖底高程) |
在σ坐标系下,本研究建立的太湖三维水动力子模型的连续性方程、动量方程以及输运方程可以改写为如下形式:
| \text{u=Rcos}\mathtt{ϕ}\frac{\text{d}λ}{\text{dt}} \;\;\;\;\;\;\; \text{v=R}\frac{\text{d}\mathtt{ϕ}}{\text{dt}} | (S18) |
| \frac{\text{∂h}}{\text{∂t}}\text{+}\frac{\text{1}}{\text{Rcos}\mathtt{ϕ}}\left(\frac{\text{∂hu}}{\text{∂}\lambda }\text{+}\frac{\text{∂hvcos}\mathtt{ϕ}}{\text{∂}\mathtt{ϕ}}\right)\text{+}\frac{\text{∂h}\mathtt{ω}}{∂\mathtt{σ}}\text{=hS} | (S19) |
| \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{\partial h u}{\partial t}+\frac{1}{R cos \phi}\left(\frac{\partial h u^2}{\partial \lambda}+\frac{\partial h v u cos \phi}{\partial \phi}\right)+\frac{\partial h \omega u}{\partial \sigma}=\left(f+\frac{u}{R} tan \phi\right) v h-\frac{1}{R cos \phi}\left(g h \frac{\partial \eta}{\partial \lambda}+\frac{1}{\rho_0} \frac{\partial p_a}{\partial \lambda}+\right.\\ \left.\frac{g}{\rho_0} \int_z^\eta \frac{\partial \rho}{\partial \lambda} d z+\frac{1}{\rho_0}\left(\frac{\partial S_{x x}}{\partial \lambda}+cos \phi \frac{\partial S_{x y}}{\partial \phi}\right)\right)+h\left(\frac{\partial}{\partial x}\left(2 A \frac{\partial v}{\partial y}\right)+\frac{\partial}{\partial y}\left(A\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\right)\right)+\frac{\partial}{\partial \sigma}\left(\frac{v_v}{h} \frac{\partial u}{\partial \sigma}\right)+h u_s S | (S20) |
| \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{\partial h v}{\partial t}+\frac{1}{R cos \phi}\left(\frac{\partial h u v}{\partial \lambda}+\frac{\partial h v^2 cos \phi}{\partial \phi}\right)+\frac{\partial h \omega v}{\partial \sigma}=-\left(f+\frac{u}{R} tan \phi\right) u h-\frac{1}{R}\left(g h \frac{\partial \eta}{\partial \phi}+\frac{1}{\rho_0} \frac{\partial p_a}{\partial \phi}+\right.\\ \left.\frac{g}{\rho_0} \int_z^\eta \frac{\partial \rho}{\partial \phi} d z+\frac{1}{\rho_0}\left(\frac{1}{cos \phi} \frac{\partial S_{y x}}{\partial \lambda}+\frac{\partial S_{y y}}{\partial \phi}\right)\right)+h\left(\frac{\partial}{\partial x}\left(A\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\right)+\frac{\partial}{\partial y}\left(2 A \frac{\partial v}{\partial y}\right)\right)+\frac{\partial}{\partial \sigma}\left(\frac{v_v}{h} \frac{\partial v}{\partial \sigma}\right)+h v_s S | (S21) |
式中,
在σ坐标系下,水深的控制方程为:
| \frac{\partial \mathrm{h}}{\partial t}+\frac{1}{R \cos \emptyset}\left(\frac{\partial h \bar{u}}{\partial \lambda}+\frac{\partial h \bar{v} \cos \emptyset}{\partial \emptyset}\right)=h S | (S22) |
式中,
在σ坐标系下,对紊流的模拟控制方程为:
| \frac{\partial h k}{\partial t}+\frac{1}{R cos \phi}\left(\frac{\partial h u k}{\partial \lambda}+\frac{\partial h v k cos \phi}{\partial \phi}\right)+\frac{\partial h \omega k}{\partial \sigma}=h F_k+\frac{1}{h} \frac{\partial}{\partial \sigma}\left(\frac{v_t}{\sigma_k} \frac{\partial k}{\partial \sigma}\right)+h(P+B-\varepsilon) | (S23) |
| \frac{\partial h \varepsilon}{\partial t}+\frac{1}{R cos \phi}\left(\frac{\partial h u \varepsilon}{\partial \lambda}+\frac{\partial h v \varepsilon cos \phi}{\partial \phi}\right)+\frac{\partial h \omega \varepsilon}{\partial \sigma}=h F_{\varepsilon}+\frac{1}{h} \frac{\partial}{\partial \sigma}\left(\frac{v_t}{\sigma_{\varepsilon}} \frac{\partial \varepsilon}{\partial \sigma}\right)+h \frac{\varepsilon}{k}\left(c_{1 \varepsilon} P+c_{3 \varepsilon} B-c_{2 \varepsilon} \varepsilon\right) | (S24) |
式中,
大型浅水湖泊中,风生流是重要的流态,在σ坐标系下,对风应力的模拟控制方程为:
| \overrightarrow{\tau_s}=\rho_a c_d\left|u_w\right| \overrightarrow{u_w} | (S26) |
式中,
本研究根据Wallace修改的Visser提出的光驱动下微囊藻质量密度变化的数学模型,建立了光照强度与微囊藻群体质量密度的关系,对模型中的参数未作改动。在本研究中,微囊藻群体的质量密度变化仅与所在位置的光照强度变化有关,二者之间的关系式为:
| \rho_p(t+\Delta t)=\rho_p(t)+d t \Delta t | (S27) |
| \begin{cases}d t=k_1 I e^{-I / I_0}+k_2 & I \geq I_0 \\ d t=k_3 \rho_p(t)+k_4 & I <I_0\end{cases} | (S28) |
式中,
当光强处于增大趋势且I > I0时,对3.2-2进行修正,增加了响应时间,使得微囊藻群体的质量密度变化速率下降。
| d t_w=\left.e^{-\left(t / \tau_r\right)} d t\right|_{t-\Delta t}+\left.\left(1-e^{-\left(t / \tau_r\right)}\right) d t\right|_t | (S29) |
式中,
水面的光照强度随时间变化,微囊藻在不同水深的位置,所在位置的光照强度与此时水面的光照强度关系受朗伯-比尔定律的控制。
| I_S=I_{max } sin \left(\pi t / D_L\right) | (S30) |
| I_z=I_S / e^{\eta z} | (S31) |
式中,η为水的消光系数,z表示微囊藻群体所在水层的深度,
本研究根据太湖的水文、地形数据在MIKE 3中建立了太湖三维水动力子模型,并使用2017年的水位数据和太湖中不同测点三个方向(x、y、z)的整水柱平均紊流动能数据来验证本研究建立的模型。
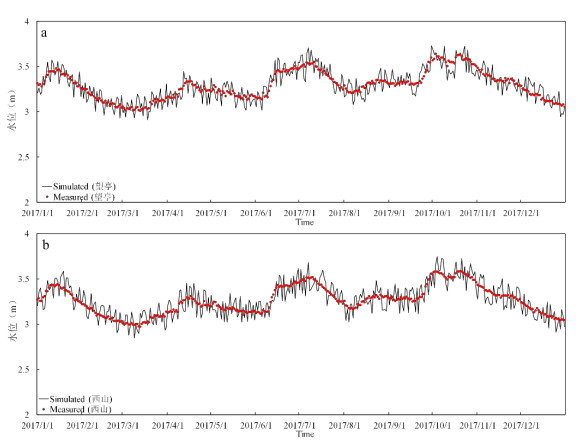
3.1 水位验证实测的水位数据来自太湖望亭、西山水文站(图2),模拟的水位数据来自本研究建立的太湖三维水动力子模型输入2017年的太湖水文、气象数据后输出的结果。对验证指标准确性的分析使用纳什系数(NSE)。结果表明,望亭水文站实测与模拟水位的纳什系数是0.88,西山水文站实测与模拟水位的纳什系数是0.90,可以认为对出入湖流量的模拟是比较准确的(附图Ⅳ)。
|
附图 Ⅳ 实测与模拟的太湖水位对比(a.望亭水文站;b.西山水文站) |
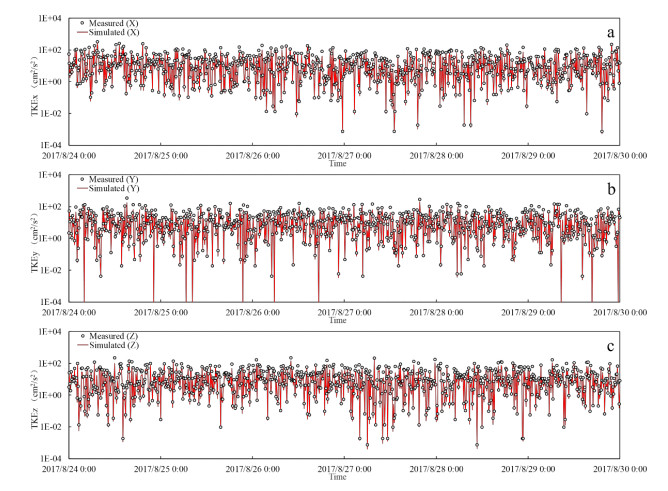
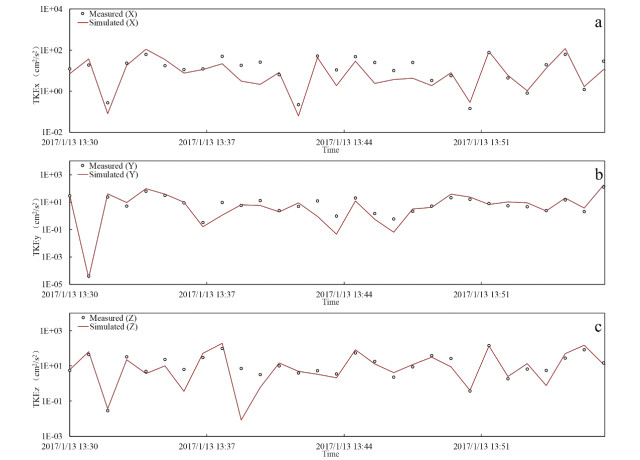
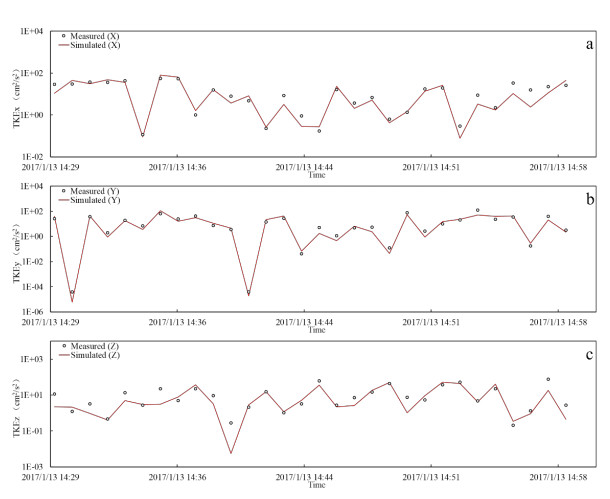
实测的紊流动能数据来自作者课题组在太湖竺山湾、贡湖湾、梅梁湾、湖心北开展的8个点的野外观测(图1),模拟的紊流动能数据来自本研究建立的太湖三维水动力子模型输入2017年的太湖水文、气象数据后在相同位置输出的结果。对验证指标准确性的分析使用纳什系数(NSE)。结果表明,8个测点的三个方向紊流动能的纳什系数都大于0.50,可以认为对太湖紊流模拟的准确性也是可以接受的(附表Ⅱ)。不同测点的实测与模拟紊流动能对比见附图Ⅴ~附图ⅩⅡ。
| 附表 Ⅱ 太湖不同测点实测与模拟紊流动能的纳什系数 |
|
附图 Ⅴ 测点1紊流动能实测值与模拟值对比 |
|
附图 Ⅵ 测点2紊流动能实测值与模拟值对比 |
|
附图 Ⅶ 测点3紊流动能实测值与模拟值对比 |
|
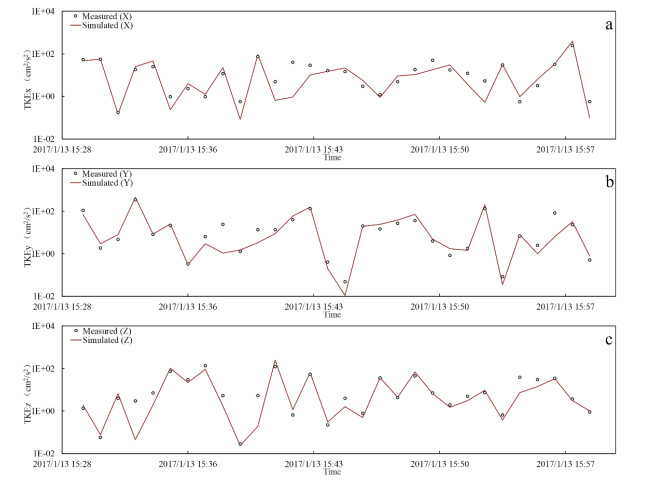
附图 Ⅷ 测点4紊流动能实测值与模拟值对比 |
|
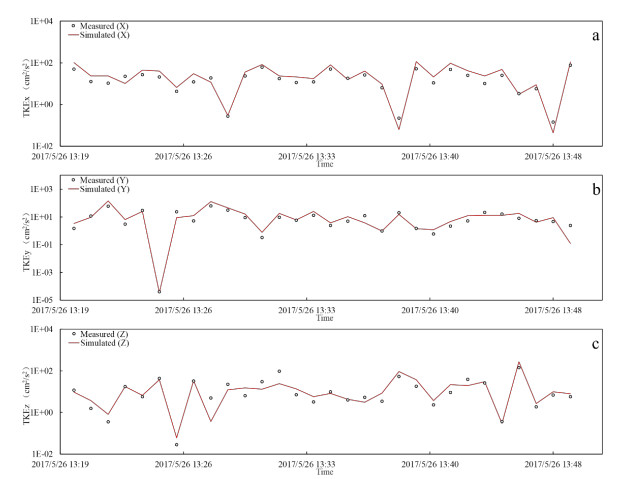
附图 Ⅸ 测点5紊流动能实测值与模拟值对比 |
|
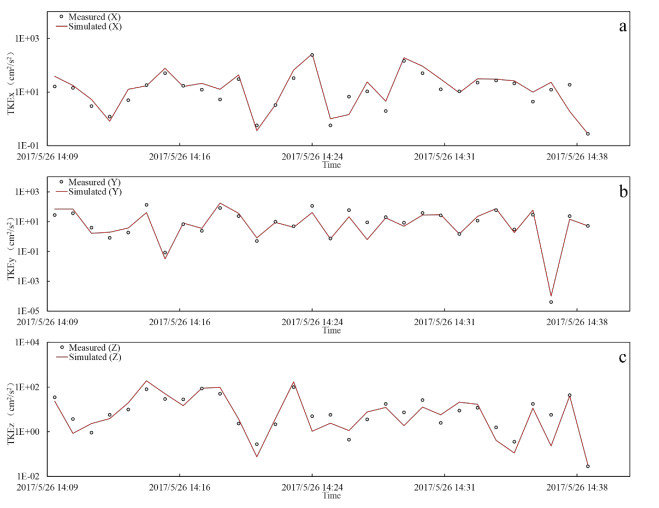
附图 Ⅹ 测点6紊流动能实测值与模拟值对比 |

|
附图 ⅩⅠ 测点7紊流动能实测值与模拟值对比 |
|
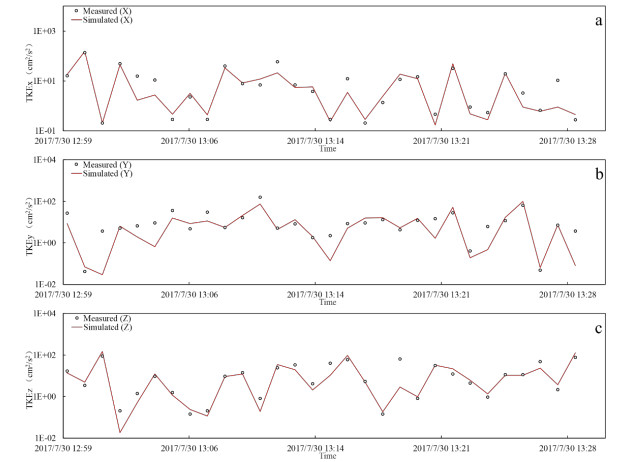
附图 ⅩⅡ 测点8紊流动能实测值与模拟值对比 |
本研究使用微囊藻迁移IBM模型,对2017年8月28日—8月29日太湖竺山湾内微囊藻迁移的过程以及2017年9月13日—14日太湖水华面积减小的过程进行反演,以此来验证我们建立的微囊藻迁移IBM模型。
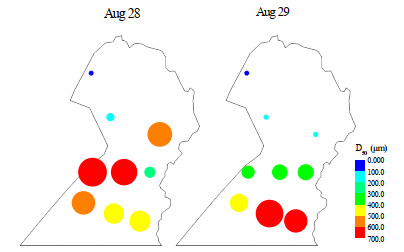
4.1 太湖竺山湾内微囊藻迁移过程的反演实测数据来自作者课题组在2017年8月28日—8月29日在太湖竺山湾9个采样点采集的藻群体粒径的d50数据和风速风向数据。通过对风场数据分析和水面藻群体粒径的d50数据分析发现,2017年8月28日—8月29日,太湖的竺山湾日均风速为2.61 m/s,主导风向为东北风和东北偏东风。这两天在竺山湾的九个固定测点实测的水面微囊藻群体的粒径d50发现,偏北的测点在8月29日测得的水面微囊藻群体粒径的d50比前一天要小,偏南的测点在8月29日测得的水面微囊藻群体粒径的d50比前一天要大(附图ⅩⅢ)。因此可以认为,这段时间内,大粒径的微囊藻群体在向西南移动,与主导风向的方向一致。
|
附图 ⅩⅢ 太湖竺山湾实测的微囊藻d50 |
模拟数据来自本研究建立的微囊藻迁移IBM模型模拟的大粒径微囊藻群体(d=600 μm)在同期太湖流场中的迁移(2017年8月28日—8月29日)。同期的太湖流场数据来自本研究建立的太湖三维水动力子模型的输出。通过微囊藻群体质量密度子模型,我们模拟了迁移过程中微囊藻群体质量密度的变化,初始的微囊藻质量密度根据多年采样结果设置为985 kg/m3。初始微囊藻群体放置的位置距离水底1.6 m。考虑到紊流影响的随机性,本研究在模拟的大粒径微囊藻群体(d=600 μm)在太湖流场中的迁移时,计算了同粒径的100个群体的迁移。模拟情景设置详见附表Ⅲ。
| 附表 Ⅲ 微囊藻迁移模拟情景设置 |
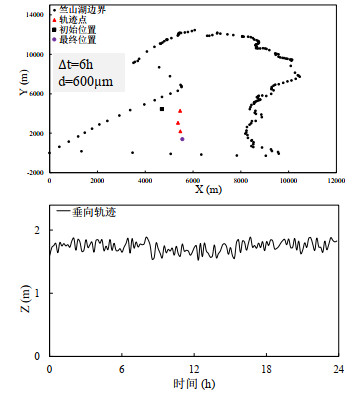
由于微囊藻的垂向分布对其水平迁移有重要影响,本研究将模拟结束后停留位置是100个群体中值的这一群体当作典型群体,将典型群体的迁移轨迹绘制于附图ⅩⅣ。由图可见,在垂向上,模拟的微囊藻群体基本漂浮在水面。而从水平迁移的轨迹来看,模拟的微囊藻群体从初始位置出发向东南方向迁移,也与同时期实测的风向相近。
|
附图 ⅩⅣ 太湖竺山湾模拟的微囊藻群体迁移轨迹 |
从实测的微囊藻微囊藻群体粒径的d50数据判断,2017年8月28日—8月29日,在太湖竺山湾主导的东北风影响下,大粒径的微囊藻群体向下风向(西南方)迁移。本研究建立的微囊藻群体IBM模型对大粒径微囊藻群体(d=600 μm)的模拟反演了该时段微囊藻群体迁移的过程。模拟结果表明,在2017年8月28日—8月29日的风速影响下(日均风速2.61 m/s),大粒径的群体基本漂浮在水面上,而水面是风生流影响强烈的区域,因此大粒径群体(d=600 μm)向下风向迁移。从模拟结果对实测结果的反演来看,本研究建立的微囊藻迁移IBM模型对微囊藻在太湖中迁移的模拟是可信的。
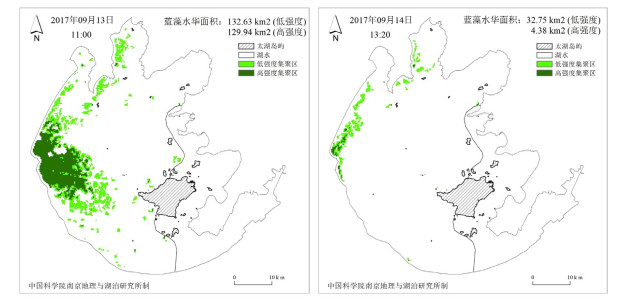
4.2 太湖水华面积减小的反演实测数据来自国家科技基础条件平台—国家地球系统科学数据中心-湖泊-流域分中心对MODIS卫星拍摄的太湖水面照片的分析。结果表明,2017年9月13日—14日,太湖水华面积由262.57 km2减少至37.13 km2,水华暴发最严重的区域也由西部沿岸区的南侧变为西部沿岸区的北侧(附图ⅩⅤ)。两次卫星照片拍摄时刻的风速由2017年9月13日的4.1 m/s变为2017年9月14日的6.7 m/s,盛行风向是东北风(NE)。
|
附图 ⅩⅤ 太湖水华面积变化 |
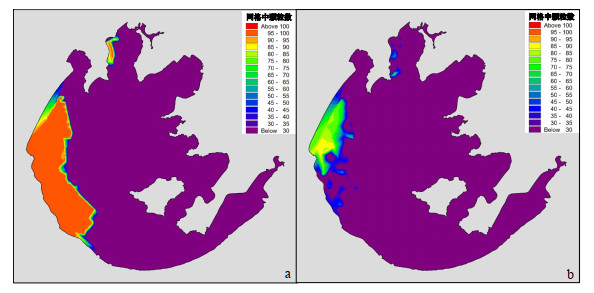
模拟数据来自本研究建立的微囊藻迁移IBM模型模拟的大粒径微囊藻群体(d=600 μm)在同期太湖流场中的迁移(2017年9月13日—9月14日)。同期的太湖流场数据来自本研究建立的太湖三维水动力子模型的输出。通过微囊藻群体质量密度子模型,我们模拟了迁移过程中微囊藻群体质量密度的变化,初始的微囊藻质量密度根据多年采样结果设置为985 kg/m3。初始的微囊藻群体根据2017年9月13日水华暴发的区域,在水华暴发相应位置的网格内都放置100个大粒径的微囊藻群体,距水面均为0.05 m(附图ⅩⅥa)。模拟情景设置详见附表Ⅳ。
|
附图 ⅩⅥ 表层颗粒分布(a.初始状态;b.最终状态) |
| 附表 Ⅳ 水华面积变化模拟情景设置 |
模拟的结果表明,2017年9月13—14日,大部分群体都在盛行风(东北风)的驱动下,向西南转移,在太湖西部沿岸区的边界堆积(附图ⅩⅥb)。但是由于2017年9月14日卫星拍摄前三小时开始,风速维持在6m/s以上,卫星拍摄时刻的风速更是达到了6.7 m/s,大部分群体都难以维持在水面,因此水华面积减小(附图ⅩⅥb)。从模拟结果对实测结果的反演来看,本研究建立的微囊藻迁移IBM模型对太湖水华面积变化的模拟是可信的。
| [1] |
Huang JC, Zhang YJ, Arhonditsis GB et al. The magnitude and drivers of harmful algal blooms in China's lakes and reservoirs: A national-scale characterization. Water Research, 2020, 181: 115902. DOI:10.1016/j.watres.2020.115902 |
| [2] |
Wang Q, Niu Y, Xie P et al. Factors affecting temporal and spatial variations of microcystins in Gonghu Bay of Lake Taihu, with potential risk of microcystin contamination to human health. The Scientific World Journal, 2010, 10: 1795-1809. DOI:10.1100/tsw.2010.172 |
| [3] |
Wu XQ, Noss C, Liu L et al. Effects of small-scale turbulence at the air-water interface on microcystis surface scum formation. Water Research, 2019, 167: 115091. DOI:10.1016/j.watres.2019.115091 |
| [4] |
Li M, Xiao M. In situ growth rate of microcystis in a hypertrophic lake: RNA/DNA ratio as an indicator. Fresenius Environ Bull, 2014, 23: 1100-1106. |
| [5] |
Reynolds CS, Walsby AE. Water-Blooms. Biological Reviews, 1975, 50(4): 437-481. DOI:10.1111/j.1469-185x.1975.tb01060.x |
| [6] |
Chen HM, Zhu YY, Zhang Y et al. Cyanobacterial bloom expansion caused by typhoon disturbance in Lake Taihu China. Environmental Science and Pollution Research, 2020, 27(34): 42294-42303. DOI:10.1007/s11356-020-09292-0 |
| [7] |
Zhu W, Zhou XH, Chen HM et al. High nutrient concentration and temperature alleviated formation of large colonies of Microcystis: Evidence from field investigations and laboratory experiments. Water Research, 2016, 101: 167-175. DOI:10.1016/j.watres.2016.05.080 |
| [8] |
Feng GY, Liu JB, Li HB et al. Insights from colony formation: The necessity to consider morphotype when assessing the effect of antibiotics on cyanobacteria. Water Research, 2023, 246: 120704. DOI:10.1016/j.watres.2023.120704 |
| [9] |
Kromkamp JC, Mur LR. Buoyant density changes in the cyanobacterium Microcystis aeruginosa due to changes in the cellular carbohydrate content. FEMS Microbiology Letters, 1984, 25(1): 105-109. DOI:10.1111/j.1574-6968.1984.tb01384.x |
| [10] |
Ibelings BW, Mur LR, Walsby AE. Diurnal changes in buoyancy and vertical distribution in populations of Microcystis in two shallow lakes. Journal of Plankton Research, 1991, 13(2): 419-436. DOI:10.1093/plankt/13.2.419 |
| [11] |
Xue ZP, Zhu W, Zhu YY et al. Influence of wind and light on the floating and sinking process of Microcystis. Scientific Reports, 2022, 12(1): 5655. DOI:10.1038/s41598-022-08977-5 |
| [12] |
Steinbuck JV, Stacey MT, McManus MA et al. Observations of turbulent mixing in a phytoplankton thin layer: Implications for formation, maintenance, and breakdown. Limnology and Oceanography, 2009, 54(4): 1353-1368. DOI:10.4319/lo.2009.54.4.1353 |
| [13] |
Wu TF, Qin BQ, Brookes JD et al. The influence of changes in wind patterns on the areal extension of surface cyanobacterial blooms in a large shallow lake in China. Science of the Total Environment, 2015, 518/519: 24-30. DOI:10.1016/j.scitotenv.2015.02.090 |
| [14] |
Chen HM, Zhu W, Wang RC et al. Rapid horizontal accumulation and bloom formation of the cyanobacterium Microcystis under wind stress. Hydrobiologia, 2023, 850(1): 123-135. DOI:10.1007/s10750-022-05048-8 |
| [15] |
Deng JC, Chen F, Liu X et al. Horizontal migration of algal patches associated with cyanobacterial blooms in an eutrophic shallow lake. Ecological Engineering, 2016, 87: 185-193. DOI:10.1016/j.ecoleng.2015.12.017 |
| [16] |
Cao HS, Kong FX, Luo LC et al. Effects of wind and wind-induced waves on vertical phytoplankton distribution and surface blooms of Microcystis aeruginosa in Lake Taihu. Journal of Freshwater Ecology, 2006, 21(2): 231-238. DOI:10.1080/02705060.2006.9664991 |
| [17] |
Wu XD, Kong FX, Chen YW et al. Horizontal distribution and transport processes of bloom-forming Microcystis in a large shallow lake(Taihu, China). Limnologica, 2010, 40(1): 8-15. DOI:10.1016/j.limno.2009.02.001 |
| [18] |
Li M, Zhu W, Gao L. Analysis of cell concentration, volume concentration, and colony size of Microcystis via laser particle analyzer. Environmental Management, 2014, 53(5): 947-958. DOI:10.1007/s00267-014-0252-8 |
| [19] |
Ranjbar MH, Hamilton DP, Etemad-Shahidi A et al. Individual-based modelling of cyanobacteria blooms: Physical and physiological processes. Science of the Total Environment, 2021, 792: 148418. DOI:10.1016/j.scitotenv.2021.148418 |
| [20] |
Grimm V, Berger U, Bastiansen F et al. A standard protocol for describing individual-based and agent-based models. Ecological Modelling, 2006, 198(1/2): 115-126. DOI:10.1016/j.ecolmodel.2006.04.023 |
| [21] |
Feng T, Wang C, Wang PF et al. How physiological and physical processes contribute to the phenology of cyanobacterial blooms in large shallow lakes: A new Euler-Lagrangian coupled model. Water Research, 2018, 140: 34-43. DOI:10.1016/j.watres.2018.04.018 |
| [22] |
Ranjbar MH, Hamilton DP, Etemad-Shahidi A et al. Impacts of atmospheric stilling and climate warming on cyanobacterial blooms: An individual-based modelling approach. Water Research, 2022, 221: 118814. DOI:10.1016/j.watres.2022.118814 |
| [23] |
Feng GY, Zhu W, Xue ZP et al. Structural variations increase the upper limit of colony size of Microcystis: Implications from laboratory cultures and field investigations. Journal of Phycology, 2020, 56(6): 1676-1686. DOI:10.1111/jpy.13054 |
| [24] |
中华人民共和国国家发展和改革委员会. 太湖流域水环境综合治理总体方案(2013年修编), 2013.
|
| [25] |
Hu WP. A review of the models for Lake Taihu and their application in lake environmental management. Ecological Modelling, 2016, 319: 9-20. DOI:10.1016/j.ecolmodel.2015.07.028 |
| [26] |
Xue ZP, Zhu W, Bai S et al. Wind-driven post-bloom dispersion of Microcystis in a large shallow eutrophic lake: A case study in Lake Taihu. Science of the Total Environment, 2024, 941: 173512. DOI:10.1016/j.scitotenv.2024.173512 |
| [27] |
Xue ZP, Zhu W, Cheng L et al. Wind-driven hydrodynamic characteristics of Lake Taihu, a large shallow lake in China. Environmental Science and Pollution Research, 2024, 31(17): 26123-26140. DOI:10.1007/s11356-024-32930-w |
| [28] |
Wallace BB, Hamilton DP. Simulation of water-bloom formation in the Cyanobacterium Microcystis aeruginosa. Journal of Plankton Research, 2000, 22(6): 1127-1138. DOI:10.1093/plankt/22.6.1127 |
| [29] |
Feng GY, Zhu W, Hu SY et al. Attenuation of light influences the size of Microcystis colonies. Harmful Algae, 2019, 89: 101667. DOI:10.1016/j.hal.2019.101667 |
| [30] |
Maxey MR, Riley JJ. Equation of motion for a small rigid sphere in a nonuniform flow. The Physics of Fluids, 1983, 26(4): 883-889. DOI:10.1063/1.864230 |
| [31] |
Tang YM, Ren FJ, Pedrycz W. Fuzzy C-Means clustering through SSIM and patch for image segmentation. Applied Soft Computing, 2020, 87: 105928. DOI:10.1016/j.asoc.2019.105928 |
| [32] |
Li M, Zhu W, Guo LL et al. To increase size or decrease density? Different Microcystis species has different choice to form blooms. Scientific Reports, 2016, 6: 37056. DOI:10.1038/srep37056 |
| [33] |
Li Q, Bou-Zeid E, Vercauteren N et al. Signatures of air-wave interactions over a large lake. Boundary-Layer Meteorology, 2018, 167(3): 445-468. DOI:10.1007/s10546-017-0329-z |
| [34] |
Tse IC, Poindexter CM, Variano EA. Wind-driven water motions in wetlands with emergent vegetation. Water Resources Research, 2016, 52(4): 2571-2581. DOI:10.1002/2015wr017277 |
| [35] |
Qin BQ, Hu WP, Chen WM et al. Studies on the hydrodynamic processes and related factors in Meiliang Bay, northern Taihu Lake, China. J Lake Sci, 2000, 12(4): 327-334, 385. [秦伯强, 胡维平, 陈伟民等. 太湖梅梁湾水动力及相关过程的研究. 湖泊科学, 2000, 12(4): 327-334, 385. DOI:10.18307/2000.0406] |
| [36] |
Wang JW, Li YP, Luo LC et al. Field observation of vertical shear of wind-driven current in Taihu Lake. Water Resources Protection, 2016, 32(6): 98-103, 116. [王建威, 李一平, 罗潋葱等. 太湖风生流垂向切变规律的原位观测. 水资源保护, 2016, 32(6): 98-103, 116. DOI:10.3880/j.issn.1004-6933.2016.06.016] |
| [37] |
Nutz A, Schuster M, Ghienne JF et al. Wind-driven bottom currents and related sedimentary bodies in Lake Saint-Jean(Québec, Canada). Geological Society of America Bulletin, 2015, 127(9/10): 1194-1208. DOI:10.1130/b31145.1 |
| [38] |
Zhu W, Cheng L, Xue ZP et al. Changes of water exchange cycle in Lake Taihu(1986-2018) and its effect on the spatial pattern of water quality. J Lake Sci, 2021, 33(4): 1087-1099. [朱伟, 程林, 薛宗璞等. 太湖水体交换周期变化(1986—2018年)及对水质空间格局的影响. 湖泊科学, 2021, 33(4): 1087-1099. DOI:10.18307/2021.0411] |
| [39] |
Soontiens N, Binding CR, Fortin V et al. Algal bloom transport in Lake Erie using remote sensing and hydrodynamic modelling: Sensitivity to buoyancy velocity and initial vertical distribution. Journal of Great Lakes Research, 2019, 45(3): 556-572. DOI:10.1016/j.jglr.2018.10.003 |
| [40] |
Hozumi A, Ostrovsky I, Sukenik A et al. Turbulence regulation of Microcystis surface scum formation and dispersion during a cyanobacteria bloom event. Inland Waters, 2020, 10(1): 51-70. DOI:10.1080/20442041.2019.1637681 |
| [41] |
Wang W, Shen SH, Liu SD et al. Mechanistic analysis of the observed energy imbalance of Lake Taihu. Acta Ecologica Sinica, 2017, 37(18): 5935-5950. |
| [42] |
George DG. Wind-induced water movements in the south basin of Windermere. Freshwater Biology, 1981, 11(1): 37-60. DOI:10.1111/j.1365-2427.1981.tb01241.x |
| [43] |
Wu HM, Wu XQ, Yang TT et al. Feedback regulation of surface scum formation and persistence by self-shading of Microcystis colonies: Numerical simulations and laboratory experiments. Water Research, 2021, 194: 116908. DOI:10.1016/j.watres.2021.116908 |
| [44] |
Shi K, Zhang YL, Zhang YB et al. Phenology of phytoplankton blooms in a trophic lake observed from long-term MODIS data. Environmental Science & Technology, 2019, 53(5): 2324-2331. DOI:10.1021/acs.est.8b06887 |
| [45] |
水利部太湖流域管理局. 太湖健康状况报告, 2017.
|
| [46] |
Guan DX, Wang XY, Xu HC et al. Temporal and spatial distribution of Microcystis biomass and genotype in bloom areas of Lake Taihu. Chemosphere, 2018, 209: 730-738. DOI:10.1016/j.chemosphere.2018.06.141 |
| [47] |
Han ZP, Shao CG, Zhang ZS et al. Annual variations of blue algae biomass and TN and TP levels and their correlation at different inlet areas of South Taihu Lake. Oceanologia et Limnologia Sinica, 2012, 43(5): 911-918. [韩志萍, 邵朝纲, 张忠山等. 南太湖入湖口蓝藻生物量与TN、TP的年变化特征及相关性研究. 海洋与湖沼, 2012, 43(5): 911-918.] |
 2024, Vol. 36
2024, Vol. 36 


