摘要
不同区域具有不同的地理和气候条件,对于极端降雨的影响规律不尽相同;深入、准确地剖析太湖流域极端降雨对城镇化进程的响应规律,对于预测和减轻未来极端天气事件的潜在影响至关重要。因此,本研究通过考虑区域异质性,构造了城市、乡镇、农村不同地区、不同类型的城镇化因子矩阵;将位置参数建模为随气候变化因子、本地因子、邻近城市因子和邻近乡镇因子变化的函数,构建了反映不同地区、不同速度的城镇化进程对极端降雨影响的时变广义极值分布模型,揭示了太湖流域极端降雨对城镇化的响应规律。结果显示:不同模型的对比表明有必要在极端降雨模型中考虑气候变化和城镇化的影响,且不仅要考虑本地城镇化的影响,还要考虑周围地区城镇化的影响;受城镇化的驱动影响,太湖流域极端降雨的量级整体增大,且更为集中;城镇化的影响使得太湖流域极端降雨量级的重现水平在城市区域增加36.0%、乡镇区域增加25.2%、农村区域增加31.6%,极端降雨累积强度的重现水平在城市区域增加16.8%、乡镇区域增加35.2%、农村区域增加24.4%。本研究考虑区域异质性,构建了一个全面反映不同地区、不同速度的城镇化对极端降雨影响的评估框架,深化了气候变化、城镇发展与极端降水交互作用的认识,为制定更为精准的气候适应策略及城市规划提供了科学依据。
Abstract
Varied in geographic and climatic conditions, many regions have different influence patterns on extreme precipitation. An in-depth analysis of the response pattern of extreme precipitation to urbanization is essential for predicting and mitigating the potential impacts of future extreme weather events. In this study, different types of urbanization factor matrices for the cities, towns and rural areas in Taihu Basin are constructed by considering regional heterogeneity. The location parameters are modelled as a function of variation with climate change factor, local factor, neighboring city factor and neighboring township factor. A time-varying non-stationary generalized extreme value distribution model reflecting the impact of urbanization processes on extreme precipitation in varied regions and rates is constructed. The response pattern of extreme precipitation to urbanization in the Taihu Basin is revealed. The results show that: the comparison of different models show the need to consider the impacts of climate change and urbanization in extreme precipitation models, and not only the impacts of local urbanization, but also the impacts of urbanization in surrounding areas. Driven by urbanization, the magnitude of extreme precipitation in Taihu Basin increases overall and becomes more concentrated around a certain value. The urbanization increases the recurrence level of the magnitude of extreme precipitation in Taihu Basin by 36.0% in city areas, 25.2% in townships and 31.6% in rural areas, and increases the recurrence level of the cumulative intensity of extreme precipitation by 16.8% in city areas, 35.2% in townships and 24.4% in rural areas. Considering regional heterogeneity, this study constructs an assessment framework that comprehensively reflects the impacts of urbanization on extreme precipitation in different regions and rates, deepens the understanding of the interactions between climate change, urban development and extreme precipitation, and provides a scientific basis for formulating more accurate climate adaptation strategies and urban planning.
Keywords
随着全球气候变化和城镇化进程的快速发展,极端降水事件增多,太湖流域作为典型的高度城镇化地区,其洪涝灾害问题日益突出,成为制约经济社会发展的重要因素。城镇化过程所导致的气溶胶排放增加、下垫面急剧变化、城市热岛效应不断增强等,使得大气热量、动力条件、城市环境组分等发生变化,这些变化驱动着小尺度局地气候发生显著改变,影响了极端降水的形成和分布。
在城市化对极端降水的影响研究方面,物理模拟和统计分析是当前比较流行的方法[1-4]。Yang等利用天气研究与预报(WRF)模型研究了大型城市化地区的降雨时空分布规律[5]。Zhang等利用耦合多层城市冠层方案的天气研究和预报模型揭示了城市化对区域极端降水过程的影响[6]。但是,采用物理模拟的方法存在一定的局限性,比如模型参数存在不确定性、要求高分辨率的数据以及计算成本相对较大等。而使用历史观测数据的统计分析方法需要的计算成本相对较小,适用于区域尺度的研究[7]。Golroudbary等利用统计分位数回归和分类方法,考虑露点、气温和北大西洋涛动指数与降水的相关关系,量化了荷兰极端降水对城市化的响应,结果表明城市站点最大日降水量的重现期大于非城市站点,春季以后尤其明显,差异值达到5%~7%[8]。Feng利用1961—2010年中国544个气象站逐日降水资料,研究了中国夏季极端降水对城市化的潜在响应,发现:城市化使极端降水阈值增加了1.68%;极端降水强度与城市化水平呈明显的线性相关,城市化水平增加一级,极端降水强度增加0.62%,从而得出结论:城市化的影响增加了中国夏季极端降水的风险[9]。Wu等分析了西安市土地利用和极端降水的变化特征以及城市化对极端降水的影响,研究发现:城市化使极端降水强度显著增加,但对长历时降水强度影响较小;2000年以后,城市建设用地、极端降雨频率、强度的增长趋势高度一致[10]。Wang等评价了中国珠江三角洲地区城市化与极端降水的关系,结果显示:极端降水指数的空间格局与城市范围的空间格局基本一致,二者具有显著的空间正相关性;时间尺度较短的极端指数的相关性强于时间尺度较长的极端指数的相关性,如最大5日降水与城市范围自然对数的相关系数为0.42,最大3小时降水与城市范围自然对数的相关系数为0.74[11]。以往的研究多集中在比较同一站点在不同的城市化发展阶段降雨特征(如降雨强度和持续时间)的变化[12-13],以及同一时期不同站点之间降雨特征的变化[14-17],而对于不同地区、不同速度的城市化进程对极端降雨影响的精细化量化研究尚未见报道。
由于不同区域具有不同的地理和气候条件,其对于极端降雨的影响规律也不尽相同。深入、准确地剖析城镇化进程对太湖流域极端降水的影响规律,对于认识太湖流域城镇发展与极端降水变化的关系、预测和减轻未来极端天气事件的潜在影响具有十分重要的科学意义。因此,本文通过考虑区域异质性,构造城市、乡镇和农村不同地区、不同类型的城镇化因子矩阵,据此构建反映不同地区、不同速度的城镇化进程对极端降雨影响的时变非平稳广义极值分布模型,从而剖析太湖流域极端降雨对城镇化的响应规律。
1 研究区及数据
太湖流域位于长江三角洲南缘(30°05′~32°08′N,119°08′~121°55′E),属亚热带季风气候区,四季分明,雨水丰沛。流域内分布有超大城市上海,特大城市杭州、苏州,大中城市无锡、常州、镇江、嘉兴、湖州及迅速发展的众多小城市和建制镇,城镇化率达74.7%。选择太湖流域中处于城镇化快速发展阶段的常州、无锡、苏州、嘉兴及其下辖县级市作为研究区(图1a)。上海处于城市化发展成熟阶段,故没有纳入本次研究。湖州大部分位于山区,城镇化水平不高,为了集中研究城镇化因素对极端降水的影响,而非山地环境的影响,故将湖州排除在外。本研究区中的不同地区之间城市化水平存在差异,位于江苏省的常州、无锡和苏州经济发展较快、城市化水平较高,而位于浙江省的嘉兴城市化水平相对较低。本研究中,将上述4个地级市定义为城市,其下辖县级市(区)定义为乡镇,选择分布在各区市的20个雨量站,并根据地理位置和行政区域,将其分为城市站点、乡镇站点和农村站点(图1b)。农村站点位于城市边缘,离城市不透水表面有一定距离。

图1研究区域及站点分布
Fig.1Study area and distribution of stations
20个雨量站1978—2019年逐日降水数据来源于中华人民共和国水利部太湖流域管理局及《中华人民共和国水文年鉴·长江流域水文资料》。编程将降水数据处理为年最大1日降雨序列(Max1d)和年最大5日降雨序列(Max5d),Max1d反映极端降水的量级,Max5d反映极端降水的累积强度[18]。
研究区是典型的亚热带季风气候主导的高度城镇化地区,气候变化和人类活动都是影响极端降雨的重要因素。考虑全球气候变化的影响,本研究采用与太湖流域极端降雨存在遥相关的6个大尺度气候指标作为气候变化因子。Niño3.4区海温指数(Niño3.4)表示赤道中东太平洋(5°S~5°N,120°W~170°W)区域的海温异常;南方涛动指数(SOI)用南太平洋大溪地与达尔文两地的气压差来衡量,反映厄尔尼诺现象的活跃程度;Niño3.4和SOI均为厄尔尼诺-南方涛动(ENSO)指标。北大西洋涛动(NAO)表示亚速尔高压和冰岛低压之间气压的反向变化关系。太平洋年代际振荡(PDO)表示以中纬度太平洋盆地为中心的强、周期性的海洋大气气候变化模式。东亚夏季风指数(EASMI)定义为东亚热带季风槽区与东亚副热带地区850 hPa的平均纬向风距平,反映东亚风场与降水场的年际变化特征。南中国海夏季季风指数(SCSMI)定义为南海季风区925 hPa季节性环流的动态标准化指数。Niño3.4、SOI、NAO和PDO数据来源于美国大气海洋局(NOAA)网页(https://www.esrl.noaa.gov),EASMI和SCSMI数据来源于中国海洋大学物理海洋教育部重点实验室李建平教授的主页(http://lijianping.cn)。本研究使用的数据为1978—2019年的逐年平均值。
不透水表面是衡量城镇化程度最直观和最重要的指标。众多研究表明,不透水表面与极端降雨有着密切的联系,不透水表面的扩张会改变区域气候[19-20]。因此,采用不透水表面作为城镇化因子。利用Google Earth高分辨率遥感影像,采用不透水面指数法进行解译,提取研究区逐年不透水表面分布情况,提取精度达到90%以上。1978—2019年各城市及乡镇逐年不透水面积变化如图2所示。

图2各城市及乡镇1978—2019年不透水面积变化
Fig.2The changes of impervious area of each city and town from 1978 to 2019
2 研究方法
2.1 非平稳广义极值分布模型
非平稳广义极值分布(GEV)模型在参数项中引入协变量来表征参数的变化,具有随时间变化的特征。忽略环境过程的非平稳行为可能导致对分位数的偏倚估计,而包含协变量效应的模型能够提供相对无偏的估计[21]。已有研究表明,位置参数对极值降水的变化趋势起主要作用,而形状参数的作用较小[22-23],并且,拟合中如果允许形状参数变化,可能导致数值计算方面的问题[24]。因此,本研究考虑位置参数随时间的变化,以气候变化因子和城镇化因子作为协变量,其关系采用线性函数;将尺度参数和形状参数作为常数。非平稳广义极值分布函数定义如下:
(1)
式中,x为年最大1日或5日降雨序列,μ(θ)为非平稳广义极值分布模型的位置参数,θ为位置参数的协变量,σ和ξ分别为尺度参数和形状参数。采用极大似然估计法估计模型参数。
2.2 模型构建
2.2.1 气候变化因子
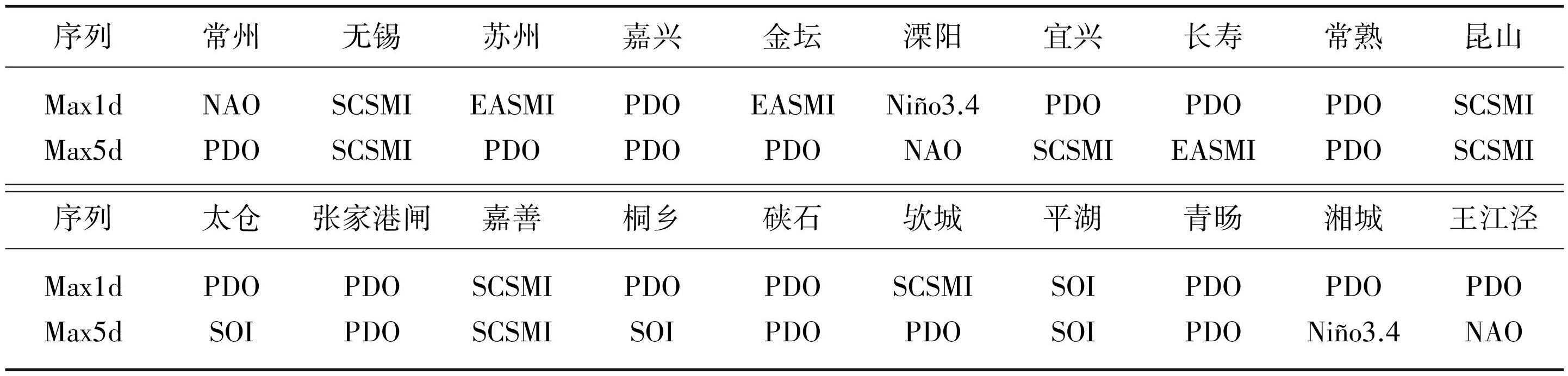
研究区极端降水的变化受亚热带季风气候影响,与Niño3.4、SOI、NAO、PDO、EASMI和SCSMI等气候指标存在遥相关[25-26]。对以上气候指标与各站点1978—2019年Max1d和Max5d序列进行相关分析,选择相关性最强的气候指标作为该序列的气候变化因子,建立随大气条件变化的非平稳模型。各序列相关性最强的气候指标如表1所示,即为各站点序列非平稳广义极值分布模型的气候变化因子Q。
表1各站点Max1d和Max5d序列的气候变化因子
Tab.1 Climate change factors matrix of Max1d and Max5d sequences at each station
2.2.2 城镇化因子矩阵
研究区各城镇1978—2019年不透水面积如图2所示,1978年,各城镇不透水面积较小,城镇化水平较低;之后,城镇不透水面积持续快速扩张,各城镇与周边区域的关系也逐渐加强。为了建立随城镇化进程变化的非平稳模型,基于不透水表面扩张过程,考虑本地城镇化、邻近区域城镇化对极端降水的影响,构造包含3个部分的城镇化因子组:本地因子A、邻近城市因子B和邻近乡镇因子C,不同类型站点的城镇化因子矩阵如图3所示。
本地因子A表示本地的不透水表面增加对极端降水的影响;随着周边城市的发展,邻近城市因子B表示周边城市的不透水表面增加对极端降水的影响;随着乡镇的扩张,邻近乡镇因子C表示周边乡镇的不透水表面增加的影响。不透水面积越大,对极端降水的影响越大;不透水表面的距离越远,对极端降水的影响越小,因此,将不透水面积作为城镇化因子的分子,将与不透水表面的距离作为城镇化因子的分母。对于城市站点,本地因子Ac为该城市本身的不透水面积。对于乡镇站点,本地因子At为该乡镇本身的不透水面积。对于农村站点,本地因子Ar为该站点所属城市的不透水面积与该站点至所属城市不透水表面最近距离的比值。这是由于农村本身没有不透水表面,这里将其所属城市的不透水表面对农村极端降雨的影响归为本地影响;并且,农村站点位于所属城市边界,与所属城市的不透水表面有一定距离。对于各类型站点,邻近城市因子B为邻近城市不透水面积与该站点至邻近城市不透水表面最近距离的比值;邻近乡镇因子C为邻近乡镇不透水面积与该站点至邻近乡镇不透水表面最近距离的比值。各站点的各城镇化因子为1978—2019年间的42个值。

图3不同类型站点的城镇化因子矩阵
Fig.3Urbanization factors matrix of different types of stations
此外,为了消除气候变化因子(Q)和城镇化因子(A、B、C)的量纲影响,采用极值法进行标准化处理后再进行建模。
2.2.3 模型构建
本研究构建的模型基本信息如表2所示,采用GEV分布,对各站点的Max1d和Max5d序列进行以下模型的拟合:
表2本研究构建的模型基本信息
Tab.2 The information of models constructed in this study

μ、μ1、μ2、μ3、μ4、μ5、σ、ξ均为常数。
①模型M0:GEV(μ,σ,ξ),所有参数均为常数。该模型是一个平稳的情况,作为参考。
②模型M1:GEV(μ(Q),σ,ξ),位置参数随气候变化因子线性变化。该模型评估了气候变化对极端降雨的影响,作为气候变化背景的非平稳情况。
③模型M2:GEV(μ(A,B,C),σ,ξ),位置参数随所有城镇化因子的变化而变化。该模型评估了城镇化进程对极端降雨的影响。
④模型M3:GEV(μ(Q,A),σ,ξ),位置参数随气候变化因子和本地城镇化因子而变化。该模型评估了气候变化和当地城镇化进程对极端降雨的影响。
⑤模型M4:GEV(μ(Q,A,B,C),σ,ξ),位置参数随气候变化因子和所有城镇化因子而变化。该模型除了评估气候变化和本地城镇化进程对极端降雨的影响,还考虑了周边城市和乡镇城镇化进程对极端降雨的影响。
2.3 模型优选
采用似然比检验(LRT)优选最佳拟合GEV模型,GEV模型的对数似然函数为:
(2)
式中,n为样本容量。LRT的检验统计量为:
(3)
式中,l1和l0分别为模型M1和模型M0的最大对数似然函数值。令k为模型M1和M0参数个数的差值,则统计量D服从自由度为k的χ2分布。D>0表示模型M1优于M0;取显著性水平为90%,若D>χ20.9(k),则模型M1显著优于M0。
2.4 重现水平计算
非平稳GEV模型的重现水平又叫“等效重现水平”,其公式如下:
(4)
式中,p为不超过概率,重现水平qp对应的重现期T=1/(1-p)。平稳情况中,重现期为T年的极端事件有两种解释:一次量级为qp的极端事件发生到下一次发生的平均间隔时间为T年;任意一年发生量级超过qp的极端事件的概率为1-p。而非平稳情况下,重现水平随协变量发生变化,因此只有第二种解释是适用的。
3 结果与讨论
3.1 模型构建及优选
为了研究太湖流域城镇化对极端降雨的影响规律,对20个雨量站的Max1d和Max5d序列进行如表2所述的平稳GEV模型(M0)和4种非平稳GEV模型(M1~M4)的拟合。采用似然比检验法进行拟合优度检验,从而判断非平稳模型相对于平稳模型是否有改进,检验结果如表3所示。M1模型与M0模型相比的统计量大于0,表示M1模型的拟合效果优于M0。90%显著性水平下,参数个数相差1、2、3、4的临界值分别为2.71、4.61、6.25、7.78,统计量大于临界值表示M1模型显著优于M0模型,在表3中加粗显示。
由表3可知,所有的非平稳模型(M1、M2、M3、M4)与平稳模型(M0)相比,统计量均大于0,即非平稳模型的拟合效果均优于平稳模型,说明有必要构建时变概率分布模型来反映极端降雨分布的非平稳性。在非平稳模型中,同时考虑气候变化和城镇化影响的M3、M4模型的拟合效果均优于仅考虑气候变化影响的M1模型,说明研究区的极端降雨受到气候变化和城镇化的双重影响;而仅考虑城镇化影响的M2模型,在绝大部分站点的拟合效果优于M1模型,表明研究区城镇化对极端降雨的影响比气候变化更大。不管是与M0模型还是与M1模型相比,考虑气候变化因子和全部城镇化因子的M4,统计量超过临界值的站点最多,即显著优于M0模型和M1模型,表明有必要在极端降雨模型中考虑气候变化和城镇化的影响,且不仅要考虑本地城镇化的影响,还要考虑周围地区城镇化的影响。总的来说,研究区极端降雨的最优模型为M4模型,下面采用P-P图直观检验M4的拟合性能,各站点Max1d和Max5d序列采用M4模型的理论概率和经验概率之间的拟合效果如图4所示。概率点均大致分布在对角线上,说明M4模型对Max1d和Max5d序列的拟合效果较好。
表3Max1d和Max5d序列拟合模型的似然比检验结果*
Tab.3 Likelihood ratio test results of Max1d and Max5d sequences fitting models
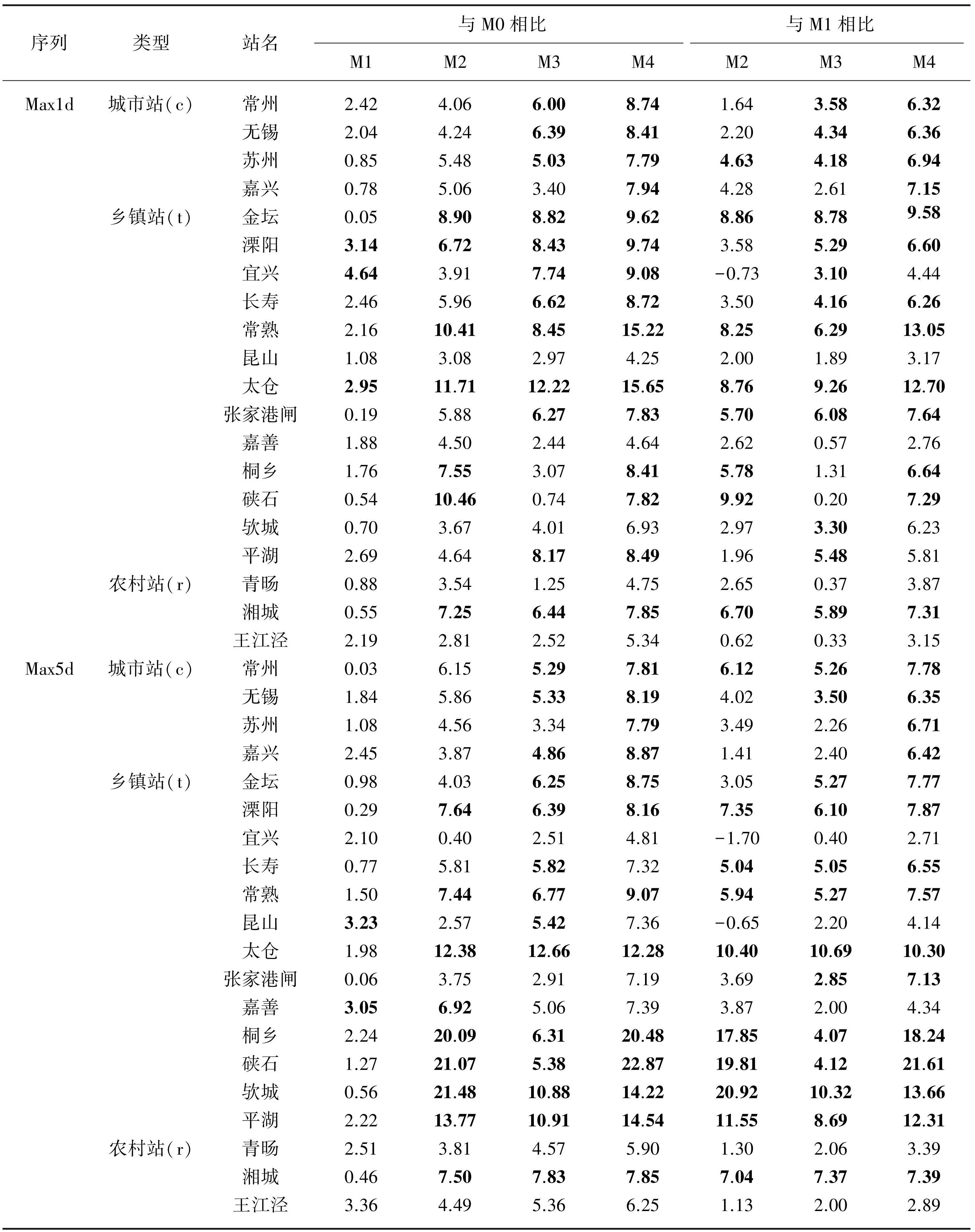
*加粗显示的统计量为超过90%显著性水平临界值的情况,即可认为模型显著优于被比较模型。

图4Max1d和Max5d序列M4模型拟合P-P图
Fig.4P-P diagram of Max1d and Max5d sequences fitting M4 model
3.2 城镇化对极端降雨的影响规律
研究区属于典型的季风气候,单纯考虑城镇化因素对极端降雨的影响不合理,因此,本研究选择了相关性强的大尺度气候指标表征气候变化,构建了M1模型。与M1模型相比,M4模型还另外考虑了本地及周边城镇化因素,本研究通过对比M1和M4模型来研究城镇化对极端降雨的影响。表3中最后一列为M4模型与M1模型相比的统计量,其中加粗显示为M4模型显著优于M1模型的站点,包括所有城市站点、大部分乡镇站点和部分农村站点,因此选择这些站点来着重研究。
M1和M4模型的差异表明快速城镇化进程对极端降雨有重要影响,Max1d和Max5d序列分别拟合M1和M4模型的概率密度函数(PDF)曲线(图5和图6),其中M1和M4模型的位置参数均取其位置参数序列的95%分位数作为典型实例[27-28]。
由图5和图6可知,与M1模型相比,M4模型的概率密度函数曲线更加陡峭狭窄,且峰值出现不同程度的右移,说明引入城镇化对极端降水的影响后,Max1d和Max5d的量级整体增大,且更加集中于某一值附近。对于Max1d序列,变化尤为明显的是城镇化水平较高的城市站点常州、无锡和苏州;对于Max5d序列,城镇化水平较高的城市站点变化仍然较为明显,且城镇化快速发展的部分乡镇站点变化更为明显,说明城镇化对于极端降雨峰值的影响在城市地区最大,对于极端降雨累积强度的影响在乡镇地区最大。对太湖流域高度城镇化下降雨特征的时空变化研究[29]发现,城镇化水平较高的地区降雨量更大,尤其是大雨和暴雨事件更易发生,这与本研究结论一致。

图5各站点Max1d序列拟合M1和M4模型的概率密度函数曲线对比
Fig.5The probability density function of M1 and M4 models fitted by Max1d sequence of each station

图6各站点Max5d序列拟合M1和M4模型的概率密度函数曲线对比
Fig.6The probability density function of M1 and M4 models fitted by Max5d sequence of each station
同时,本研究计算了分别基于M1和M4模型的10年一遇、20年一遇、50年一遇和100年一遇重现期的Max1d和Max5d重现水平,如图7和图8所示,其中M1和M4模型的位置参数使用1978—2019年逐年变化的值。

图7基于M1和M4模型的Max1d重现水平对比
Fig.7Return period of Max1d based on M1 and M4 models
图8基于M1和M4模型的Max5d重现水平对比
Fig.8Return period of Max5d based on M1 and M4 models
由图7和图8可知,随时间推移,M4模型的重现水平较M1模型呈现显著的增加趋势;M4模型10年、20年、50年和100年重现期的重现水平总体上高于M1模型,虽然少数站点刚开始基于M4模型的重现水平略低于M1模型,但随着时间推移,M4模型的重现水平迅速增加,使得近年来M4模型的重现水平仍高于M1;随着重现期的增加,两种模型之间的重现水平差异越大;以上变化特征在城镇化水平较高的城市站点和城镇化快速发展的乡镇站点尤为明显。说明受城镇化的影响,Max1d和Max5d的重现水平增大。
接着,本研究进一步以10年为步长,分别计算了基于M1和M4模型的10~100年重现期的Max1d和Max5d重现水平;然后对于城市、乡镇、农村不同类型的站点,建立了M1与M4模型模拟的重现水平之间的线性回归函数,如图9所示。引入城镇化因素对于重现水平的影响可以通过M1和M4的线性回归函数曲线与45°线(y=x)的偏离程度(即偏移角与45°的比率)来进行量化[12]。

图9城镇化对Max1d和Max5d重现水平的影响
Fig.9The effect of urbanization on the return periods of Max1d and Max5d
由图9可知,引入城镇化影响后,城市站点Max1d的重现水平增加了36.0%,乡镇站点增加了25.2%,农村站点增加了31.6%;而Max5d的重现水平在城市站点增加了16.8%,乡镇站点增加了35.2%,农村站点增加了24.4%。结果表明:对于Max1d,城镇化对极端降水峰值的影响在城镇化水平高的地区大于城镇化水平低的地区;而对于Max5d,城镇化对极端降水累积强度的影响在城镇化水平低的地区大于城镇化水平高的地区,这与前面M1和M4模型拟合的PDF曲线的变化程度一致。已有研究[30]分析了城镇化对极端降水的影响及其贡献率,结果也显示城市地区城镇化对极端降水量级和日数的指标有显著强化作用。
城镇化进程中,城市群建筑物特征通过多种机制影响城市小气候变化,从而影响极端降雨事件的发生和特性。建筑物的高度、密度、布局、材料等不仅改变了城市的热平衡和风场,还影响云的形成和降水过程。首先,建筑物通过改变地表反照率和热容量,限制空气流动,增强了城市热岛效应。热岛效应驱动城市地区形成低空辐合、高空辐散的环流,在城市及其下风地区引发大气对流和风场辐合,从而增强降水。其次,建筑物的高度和布局影响风速和风向,从而影响城市中的湍流和边界层结构。城市表面的粗糙度增加,延缓对流系统的移动速度并引起局地辐合,影响降水强度和空间分布。此外,城市地区是气溶胶的重要来源,气溶胶颗粒可以作为云凝结核,影响云滴的形成和增长,从而改变降水的性质。同时,不透水下垫面增加,减少地表水的下渗和蒸发,导致地表径流增大,在极端降水事件发生时加剧城市洪涝灾害的风险。因此,在城市规划和建筑设计时,应充分考虑这些因素,优化城市小气候,减轻城市热岛效应,改善城市环境的同时,也能在一定程度上缓解由城镇化引起的极端降雨问题。
4 结论
本研究引入基于非平稳GEV分布的变参数概率分布模型,首先,通过考虑区域异质性,构造了城市、乡镇和农村不同地区、不同类型的城镇化因子矩阵;然后,将位置参数建模为随多种因素变化的函数,包括气候变化、本地特征以及邻近城市和乡镇的影响;据此构建了反映不同地区、不同速度的城镇化进程对极端降雨影响的时变极值分布模型,揭示了太湖流域极端降雨对城镇化的响应规律。结论如下:
1)考虑气候变化因子和全部城镇化因子的M4模型对于太湖流域Max1d和Max5d的拟合效果显著优于平稳模型M0,表明有必要在极端降雨模型中考虑气候变化和城镇化的影响,且不仅要考虑本地城镇化的影响,还要考虑周围地区城镇化的影响。
2)受城镇化的驱动影响,太湖流域极端降雨的量级整体增大,且更为集中。
3)城镇化的影响使得太湖流域极端降雨量级的重现水平在城市站点增加36.0%、乡镇站点增加25.2%、农村站点增加31.6%,极端降雨累积强度的重现水平在城市站点增加16.8%、乡镇站点增加35.2%、农村站点增加24.4%。
本研究考虑区域异质性,构建了一个全面反映不同地区、不同速度的城镇化对极端降雨影响的评估框架,深化了气候变化、城镇发展与极端降水交互作用的认识,为制定气候适应策略及城市规划提供了科学依据。未来可以进一步探讨城市群建筑物特征对城市小气候变化的影响,分析太湖流域极端降雨的成因机制,例如风暴潮“三碰头”的变化与影响,从而深入探讨极端降雨对城市化的响应机理。

