降雨作为流域水文模型最重要的输入信息之一,其空间变化制约着水文预报的精度.但一般情况下,流域内雨量站点数量有限且分布不均,由各站观测的点雨量推求面雨量必然存在一定误差[1].因此,定量描述降雨空间分布的不均匀性是提高水文预报精度的重要途径.
降雨空间分布不均匀性的描述有两种途径.第1种途径是通过将流域划分为更小的计算子流域(单元),认为每个子流域上的雨量是均匀分布的,但不同单元是不同的,以此反映流域降雨量的空间不均匀性,各单元可以根据周围的观测站雨量采用空间插值方法计算得到子流域雨量[2-4].第2种途径是采用统计分布函数描述降雨在流域上的空间分布.如Warrilow等[5]提出流域的降雨量可以用负指数型概率密度函数描述,以此反映降雨的空间变化特征,由负指数型函数的特性可知,这意味着较小的降雨拥有较大的概率,而较大的降雨则拥有较小的概率. Rao等[6]采用两个极值间的均匀分布函数描述降雨的空间分布,在此基础上提出了估算山坡尺度的面平均下渗率的半解析模型.梁忠民等[7]基于统计理论提出了两种降雨概率密度函数,对降雨过程中的任一计算时段,采用拟合优度概念选择其中最优模型,在此基础上构建了一种统计产流模型;但该方法需要处理Gamma分布函数,并且在每一计算时段进行降雨统计模型的优选,增加了计算的复杂性,另外,只能进行产流计算,没有解决产流量为随机变量条件下的汇流计算问题.
为此,本文引入两个负指数型函数之差构造的概率密度函数,描述一场降雨中任一计算时段流域降雨量的空间分配,并结合超渗—蓄满垂向混合产流模型,推导出流域产流量的概率分布函数;再将流域概化成一个线性水库,建立流域汇流随机微分方程[8],推求任一时段流域出口断面流量的统计分布,从而构建一个完整的流域随机产汇流模型.
1 降雨空间分布模型 1.1 模型描述对一场降雨的任一计算时段Δt,假设流域内任一点发生某个量值的降雨量是随机的,即在空间分布上具有不均匀性和不确定性.因此,可以采用某种形式的概率密度函数描述各点降雨的空间分布情况;不同时段,这个函数的形式可以相同,但对应的参数不同.本文引入如下形式的概率密度函数:
| $ f\left( {{P_i}} \right) = c\left( {{{\rm{e}}^{ - \frac{{{P_i}}}{{{m_1}}}}} - {{\rm{e}}^{ - \frac{{{P_i}}}{{{m_2}}}}}} \right) $ | (1) |
式中,Pi为流域内任一点的降雨量(mm);m1、m2和c为参数,c=1/(m1-m2),m1和m2均为正数且m1 > m2.
1.2 参数估计根据式(1),降雨的分布函数及其均值为:
| $ F\left( {{P_i}} \right) = c \cdot {m_1} \cdot {{\rm{e}}^{ - \frac{{{P_i}}}{{{m_1}}}}} - c \cdot {m_2} \cdot {{\rm{e}}^{ - \frac{{{P_i}}}{{{m_2}}}}} $ | (2) |
| $ E\left( {{P_i}} \right) = {m_1} + {m_2} $ | (3) |
将式(3)代入式(2),消去参数m2,得:
| $ F\left( {{P_i}} \right) = c \cdot {m_1} \cdot {{\rm{e}}^{ - \frac{{{P_i}}}{{{m_1}}}}} - c\left[ {E\left( {{P_i}} \right) - {m_1}} \right]{{\rm{e}}^{ - \frac{{{P_i}}}{{E\left( {{P_i}} \right) - {m_1}}}}} $ | (4) |
假设流域中有n个雨量站,则对某一Δt的n个降雨量样本,E(Pi)可以采用样本的均值估计,则分布函数F(Pi)中仅包含m1一个参数,因此,可以采用水文计算中的优化适线法估计参数m1值.实际应用时,由于雨量站数目较少(n较小),可以将流域划分成很多个格网,根据n个观测雨量,按照地理插值法(如距离平方倒数法)插值,得到每个网格雨量,以这些网格雨量为样本进行适线估计m1,进而得到m2及c的值.
2 随机产流模型将前述估计的降雨量概率分布函数与流域水文模型耦合进行流域产流量的计算,得到产流量的概率分布,以此描述产流的空间变化.本次研究采用垂向混合的产流模型进行计算,即采用超渗产流模式进行地表产流量计算,根据降雨与土壤下渗能力的联合分布推求地表产流量的空间分布;采用蓄满产流模式进行地面以下产流量的计算,但考虑到推求下渗量与蓄水容量联合分布函数的复杂性,而且对洪水而言,地面以下径流所占比重较小,因此,本次研究中对地面以下的径流计算简化处理,不推导其分布函数,而是代之以计算分布的均值(确定值).总产流量为地表径流与地面以下径流之和,由于地表径流是以分布函数形式表示的,所以,总产流量也是以分布函数形式描述.
2.1 地表径流计算采用超渗产流模式计算地表径流.由于任一计算时段的流域各点土壤结构、类型、质地及初始土壤含水量等因素不同,导致下渗能力存在差异性.因此,引入下渗能力分配曲线[9]来描述下渗能力的空间变化:
| $ F\left( {{F_i}} \right) = 1 - {\left( {1 - \frac{{{F_i}}}{{{F_{{\rm{mm}}}}}}} \right)^{BF}} $ | (5) |
| $ {F_{{\rm{mm}}}} = \left( {1 + BF} \right){F_{\rm{m}}} $ | (6) |
式中,Fm表示流域的平均下渗能力(mm/Δt);Fmm表示流域的最大下渗能力(mm/Δt);BF为反映下渗量分布不均匀性的指数.
对式(5)求导得到下渗能力的概率密度函数:
| $ f\left( {{F_i}} \right) = \frac{{BF}}{{{F_{{\rm{mm}}}}}}{\left( {1 - \frac{{{F_i}}}{{{F_{{\rm{mm}}}}}}} \right)^{BF - 1}} $ | (7) |
对任一Δt,当雨强Pi大于下渗能力Fi时产生地表径流,即:
| $ R{S_i} = \left\{ \begin{array}{l} {P_i} - {F_i}\;\;\;{P_i} > {F_i}\\ 0\;\;\;\;\;\;\;\;\;\;{P_i} \le {F_i} \end{array} \right. $ | (8) |
根据降雨和下渗能力的联合概率分布推求地表产流量的统计分布形式:
| $ F\left( {RS} \right) = \iint\limits_{{P_i} > {F_i}} {f\left( {{F_i},{P_i}} \right){\text{d}}{F_i} \cdot {\text{d}}{P_i}} $ | (9) |
式中,F(RS)为地表产流量的概率分布函数;f(Fi, Pi)为二元随机变量(Fi, Pi)的联合概率密度函数.
假设降雨与下渗能力相互独立,进一步积分求解可得地表产流量的分布函数:
| $ F\left( {RS} \right) = \frac{{c \cdot BF}}{{{F_{{\text{mm}}}}}}\left( {r - {{\text{e}}^{ - \frac{{RS}}{{{m_1}}}}} \cdot {r_1} + {{\text{e}}^{ - \frac{{RS}}{{{m_2}}}}} \cdot {r_2}} \right) $ | (10) |
其中:
| $ \left\{ \begin{array}{l} r = \left( {{m_1} \cdot {{\rm{e}}^{ - \frac{{{P_{\min }}}}{{{m_1}}}}} - {m_2} \cdot {{\rm{e}}^{ - \frac{{{P_{\min }}}}{{{m_2}}}}}} \right)\int_0^{{F_{{\rm{mm}}}}} {{{\left( {1 - \frac{{{F_i}}}{{{F_{{\rm{mm}}}}}}} \right)}^{BF - 1}}{\rm{d}}{F_i}} \\ {r_1} = \int_0^{{F_{{\rm{mm}}}}} {\left( {{m_1} \cdot {{\rm{e}}^{ - \frac{{{F_i}}}{{{m_1}}}}}} \right){{\left( {1 - \frac{{{F_i}}}{{{F_{{\rm{mm}}}}}}} \right)}^{BF - 1}}{\rm{d}}{F_i}} \\ {r_2} = \int_0^{{F_{{\rm{mm}}}}} {\left( {{m_2} \cdot {{\rm{e}}^{ - \frac{{{F_i}}}{{{m_2}}}}}} \right){{\left( {1 - \frac{{{F_i}}}{{{F_{{\rm{mm}}}}}}} \right)}^{BF - 1}}{\rm{d}}{F_i}} \end{array} \right. $ | (11) |
式中,Pmin为某一Δt流域内的最小雨量(mm); r、r1、r2是与RS无关的系数,均可通过数值积分求解.
由式(10)可推求分布的均值及方差:
| $ \begin{array}{l} E\left( {RS} \right) = \frac{{c \cdot BF}}{{{F_{{\rm{mm}}}}}}{P_{\max }}\left( {{r_2} \cdot {{\rm{e}}^{ - \frac{{{P_{\max }}}}{{{m_2}}}}} - {r_1} \cdot {{\rm{e}}^{ - \frac{{{P_{\max }}}}{{{m_1}}}}}} \right) + \\ \frac{{c \cdot BF}}{{{F_{{\rm{mm}}}}}}\left[ {{r_1} \cdot {m_1}\left( {1 - {{\rm{e}}^{ - \frac{{{P_{\max }}}}{{{m_1}}}}}} \right) - {r_2} \cdot {m_2}\left( {1 - {{\rm{e}}^{ - \frac{{{P_{\max }}}}{{{m_2}}}}}} \right)} \right] \end{array} $ | (12) |
| $ D\left( {RS} \right) = E\left( {R{S^2}} \right) - {\left[ {E\left( {RS} \right)} \right]^2} $ | (13) |
其中:
| $ \begin{array}{l} E\left( {R{S^2}} \right) = \frac{{c \cdot BF}}{{{F_{{\rm{mm}}}}}}\\ \left\{ {\begin{array}{*{20}{l}} {{P_{\max }}^2\left( {{r_2} \cdot {{\rm{e}}^{ - \frac{{{P_{\max }}}}{{{m_2}}}}} - {r_1} \cdot {{\rm{e}}^{ - \frac{{{P_{\max }}}}{{{m_1}}}}}} \right) + 2{P_{\max }}\left( {{r_2} \cdot {m_2} \cdot {{\rm{e}}^{ - \frac{{{P_{\max }}}}{{{m_2}}}}} - {r_1} \cdot {m_1} \cdot {{\rm{e}}^{ - \frac{{{P_{\max }}}}{{{m_1}}}}}} \right)}\\ { + 2\left[ {{r_2} \cdot {m_2}^2\left( {{{\rm{e}}^{ - \frac{{{P_{\max }}}}{{{m_2}}}}} - 1} \right) - {r_1} \cdot {m_1}^2\left( {{{\rm{e}}^{ - \frac{{{P_{\max }}}}{{{m_1}}}}} - 1} \right)} \right]} \end{array}} \right\} \end{array} $ | (14) |
式中,Pmax为某一Δt流域内的最大雨量(mm).
求得地表径流均值后,土壤的平均下渗量为:E(I)=E(P)-E(RS).
2.2 地面以下径流计算按照蓄满产流模式计算地面以下产流量.采用抛物线型的流域蓄水容量—面积分配曲线[10]表征土壤缺水量的空间分布:
| $ \left\{ \begin{array}{l} \alpha = 1 - {\left( {1 - \frac{{W'}}{{{W_{{\rm{mm}}}}}}} \right)^B}\\ {W_{{\rm{mm}}}} = \left( {1 + B} \right){W_{\rm{m}}} \end{array} \right. $ | (15) |
式中,W′为流域单点蓄水容量(mm);Wmm为流域单点最大蓄水容量(mm);α为产流面积;Wm为面平均最大蓄水容量(mm);B为蓄水容量—面积分配曲线的指数.
地面以下径流量RR计算公式为:
| $ RR = \left\{ {\begin{array}{*{20}{l}} 0 & {E\left( I \right) \le 0}\\ {E\left( I \right) - {W_{\rm{m}}} + {W_{\rm{0}}} + {W_{\rm{m}}}{{\left( {1 - \frac{{A + E\left( I \right)}}{{{W_{{\rm{mm}}}}}}} \right)}^{1 + B}}} & {E\left( I \right) > 0\;{\rm{且}}E\left( I \right) + A < {W_{{\rm{mm}}}}}\\ {E\left( I \right) - {W_{\rm{m}}} + {W_{\rm{0}}}} & {E\left( I \right) > 0\;{\rm{且}}\;E\left( I \right) + A \ge {W_{{\rm{mm}}}}} \end{array}} \right. $ | (16) |
式中,RR为地面以下径流量(mm);E(I)为土壤平均下渗量(mm);A为流域初始平均土壤蓄水量W0对应的纵坐标值.
本次研究,对上述计算的地表径流,直接进入河网;对地面以下径流,先划分为壤中流及地下径流,再分别按线性水库退水处理后进入河网.
3 随机汇流模型将计算单元概化为一个无旁侧入流的线性水库,水库的入流量即为前述计算的总产流量,联立水量平衡方程及槽蓄方程,可得到流域汇流系统的演算方程组:
| $ \left\{ \begin{array}{l} QT\left( t \right) - QC\left( t \right) = \frac{{{\rm{d}}W\left( t \right)}}{{{\rm{d}}t}}\\ W\left( t \right) = {K_t} \cdot QC\left( t \right) \end{array} \right. $ | (17) |
式中,QT(t)表示随机入流过程,即前述的总产流量(m3/s);QC(t)表示随机出流过程(m3/s);W(t)为计算单元的蓄水量(m3);Kt为线性水库的蓄量常数(h).
为简化计算,假设随机入流QT(t)可以近似表示成均值偏移与一个高斯白噪声项两部分的变化过程:
| $ QT\left( t \right) = \overline {QT\left( t \right)} + \omega \left( t \right) $ | (18) |
式中,
联立求解式(17)和(18),可得到该汇流模型的随机微分方程:
| $ {\rm{d}}QC\left( t \right) = \frac{1}{{{K_t}}}\left[ {QT\left( t \right) - QC\left( t \right)} \right]{\rm{d}}t + \frac{1}{{{K_t}}}{\rm{d}}B\left( t \right) $ | (19) |
采用数值离散法对式(19)进行求解,得:
| $ \left\{ \begin{array}{l} E\left[ {QC\left( {t + \Delta t} \right)} \right] = \left( {1 - \frac{1}{{{K_t}\Delta t}}} \right)E\left[ {QC\left( t \right)} \right] + \frac{1}{{{K_t}}}E\left[ {QT\left( t \right)} \right]\Delta t\\ D\left[ {QC\left( {t + \Delta t} \right)} \right] = {\left( {1 - \frac{1}{{{K_t}\Delta t}}} \right)^2}D\left[ {QC\left( t \right)} \right] + \frac{1}{{K_t^2}}D\left[ {QT\left( t \right)} \right]\Delta {t^2} \end{array} \right. $ | (20) |
根据式(20)即可推求每一计算时段出流的均值与方差,在随机项为高斯白噪声的假设下,即可得到任一时段计算单元出口流量过程的概率分布.
4 防洪风险率分析河道防洪的水文风险率R,可表示为河道洪水超过防洪安全泄量Qs的概率:
| $ R = P\left( {QC\left( t \right) \ge {Q_{\rm{s}}}} \right) = \int_{{Q_{\rm{s}}}}^{ + \infty } {f\left( {QC} \right){\rm{d}}QC} $ | (21) |
式中,f(QC)为流域出口流量过程的概率密度函数.
5 实例研究 5.1 流域概况以淮河支流黄泥庄流域为研究对象,对模型进行应用研究.黄泥庄流域面积805 km2;多年平均降水量1077 mm,但时空分布不均,年内集中于6—9月,占全年降水量的50%~80%;属于暴雨洪水多发区,场次降雨中暴雨强度时程变化大,暴雨中心范围小,洪水具有陡涨陡落的特点.流域及其雨量站点分布见图 1.
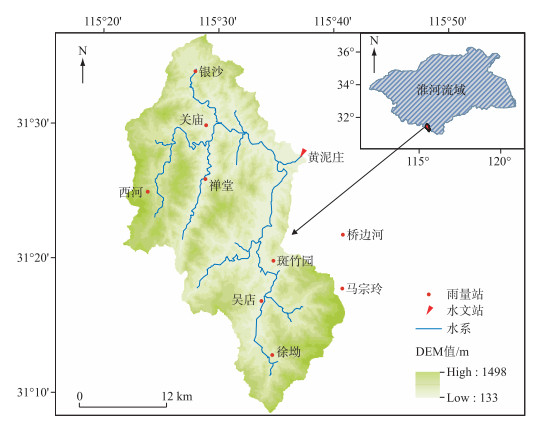
|
图 1 黄泥庄流域及其雨量站点分布 Fig.1 Geographical position and rain gauging network of Huangnizhuang Basin |
先将流域划分为10×10共100个网格,再采用距离平方倒数法由流域及其附近的10个雨量站观测数据插值得到各网格的雨量,据此估计每一计算时段的降雨空间统计分布参数m1、m2和c.选用黄泥庄水文站的16场实测次洪资料对模型进行模拟验证,其中12场用于率定,4场用于检验,计算时段Δt=1 h.
5.3 结果分析模型参数率定结果见表 1. 表 2为采用随机产汇流模型计算的16场洪水概率分布的期望值过程的精度统计结果,其中包括洪峰期望值相对误差、期望值过程洪量相对误差及确定性系数.
| 表 1 模型参数率定值 Tab.1 Calibrated parameter values of the model |
| 表 2 模型计算结果统计 Tab.2 Calibration and validation results of the model |
从表 2可以看出,考虑降雨空间变异性的随机产汇流模型计算期望值的过程,其平均确定性系数约为0.82,其中最小为0.71,最大为0.92;洪峰相对误差绝对值平均为11.3%,其中最小为0.2%,最大为22.4%;洪量相对误差绝对值平均为11.8%,其中最小为1.6%,最大为31.5%.结果表明,该模型在黄泥庄流域取得了较好的应用效果. 图 2给出了验证期两场洪水的模型计算与实测流量的对比;作为示例,图 3给出了19950624次洪、20050902次洪第4个时段及各自雨峰时段的雨量空间统计分布估计结果.

|
图 2 洪号19890510(a)和20050710(b)的模型计算与实测流量对比 Fig.2 Comparison between simulated and observed flow for flood event (No.19890510 (a) and No.20050710 (b)) |

|
图 3 流域降雨空间统计分布估计结果:(a)19950624次洪第4个时段; (b)19950624次洪雨峰时段; (c)20050902次洪第4个时段; (d)20050902次洪雨峰时段 Fig.3 Estimation results of statistical distribution of rainfall for flood event: (a)No.19950624 at the fourth time; (b) No.19950624 at the rainfall peak time; (c) No.20050902 at the fourth time; (d) No.20050902 at the rainfall peak time |
当获得洪水过程的概率密度函数后,可按式(21)计算防洪风险率,以此分析评价防洪风险.以19830625场次洪水为例,洪峰流量分布函数的期望值为1100 m3/s,标准差为280 m3/s. 图 4为正态分布假设下该场洪水洪峰流量的概率密度函数.

|
图 4 洪号19830625洪峰流量概率密度函数 Fig.4 Probability density function of flood peak for flood event (No.19830625) |
根据式(21)计算该洪峰流量超过设计洪峰流量的概率,结果列于表 3. 图 5显示了随机产汇流模型计算的洪水过程概率分布期望值、新安江模型确定性预报的结果.
| 表 3 不同重现期下设计洪峰流量及其超过概率 Tab.3 Designed peak flow and its probability in different return periods |
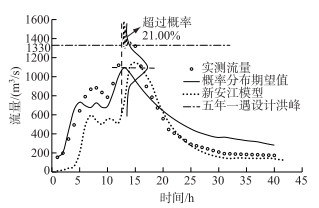
|
图 5 洪号19830625洪水风险分析示意图 Fig.5 Schematic diagram of flood risk analysis for flood event (No.19830625) |
分析表明,采用本文随机产汇流模型计算的洪峰流量期望值,其超过5年一遇设计洪峰流量(1330 m3/s)的概率较大,为21.00%,而超过10年一遇的可能性已很小,低于1%,几乎不可能超过20年一遇洪峰(2230 m3/s),概率近似为0.但是,若采用新安江模型的确定性预报结果,其洪峰预报值为1150 m3/s,认为不会超过5年一遇,防洪是安全的;而实际上,该场洪水实测洪峰流量为1350 m3/s,超过了5年一遇.由此表明,采用本文的随机产汇流模型,可以提供概率预报结果,从而可对防洪风险进行评估,更具实用价值.
6 结论在考虑降雨空间分布不均匀性的基础上,构建了一个完整的流域随机产汇流模型, 主要结论为:
1) 引入两个负指数型函数之差构造新函数,估计降雨过程中任一计算时段降雨量的概率分布函数,以此描述降雨量的空间变化特征.
2) 将降雨量分布函数与一种垂向混合的流域水文模型耦合,推导了产流量的概率分布函数,以此反映产流过程的空间变化;将流域概化成一个线性水库,并采用高斯白噪声项简化随机入流(产流)过程,从而构建流域汇流的随机微分方程,最终可得到洪水过程任一时段流量的概率分布.
3) 以淮河黄泥庄流域为例进行了应用研究,通过对16场次洪资料的模拟与验证,模型精度较好.根据计算的洪水过程概率分布函数,可进行防洪风险分析,提供比传统确定性模型更为丰富的预报信息.
| [1] |
Liang ZM, Jiang XL, Cao YX et al. Probabilistic flood forecasting considering rainfall uncertainty. Journal of Hohai University:Natural Sciences, 2016, 44(1): 8-12. [梁忠民, 蒋晓蕾, 曹炎煦等. 考虑降雨不确定性的洪水概率预报方法. 河海大学学报:自然科学版, 2016, 44(1): 8-12.] |
| [2] |
Shi P, Rui XF. Comparison and improvement of spatial rainfall interpolation methods. Journal of Hohai University:Natural Sciences, 2005, 33(4): 361-365. [石朋, 芮孝芳. 降雨空间插值方法的比较与改进. 河海大学学报:自然科学版, 2005, 33(4): 361-365.] |
| [3] |
Lebrenz H, Bárdossy A. Reconstruction of missing precipitation data. In:Copernicus. EGU general assembly conference abstracts, 2016.
|
| [4] |
Yan ZQ, Xia J, Lars G. Mapping runoff based on water balance:A case study of the Huaihe River Basin above Bengbu. Acta Geographica Sinica, 2010, 65(7): 841-852. [严子奇, 夏军, Gottschalk Lars. 基于水文随机方法的大尺度径流空间插值图化研究——淮河流域蚌埠以上区间为例. 地理学报, 2010, 65(7): 841-852. DOI:10.11821/xb201007008] |
| [5] |
Warrilow DA, Sangster AB, Slingo A. Modelling of land surface processes and their influence on European climate. Met O 20 Dynamical Climatology Technical Note 38. Bracknell:Met. office, 1986.
|
| [6] |
Rao SG, Corradini C, Morbidelli R. A semi-analytical model of expected areal-average infiltration under spatial heterogeneity of rainfall and soil saturated hydraulic conductivity. Journal of Hydrology, 2006, 316(1): 184-194. |
| [7] |
Liang ZM, Shi Y, Li BQ et al. Runoff-yield model based on statistical theory. Advances in Water Science, 2009, 20(6): 789-793. [梁忠民, 施晔, 李彬权等. 基于统计理论的产流模型. 水科学进展, 2009, 20(6): 789-793.] |
| [8] |
Sun YN, Rui XF, Fu Q et al. Basin flow concentration model based on stochastic differential equation. Journal of Hydraulic Engineering, 2011, 42(2): 187-191. [孙颖娜, 芮孝芳, 付强等. 基于随机微分方程的流域汇流模型. 水利学报, 2011, 42(2): 187-191.] |
| [9] |
Bao WM. Hydrological forecasting. Beijing: China Water & Power Press, 2009, 195. [包为民. 水文预报: 第4版. 北京: 中国水利水电出版社, 2009, 195.]
|
| [10] |
Horton RE. An approach toward a physical interpretation of infiltration-capacity. Soil Science Society of America Journal, 1941, 5(C). DOI:10.2136/sssaj1941.036159950005000C0075x |
 2018, Vol. 30
2018, Vol. 30 


