(2: 福州大学, 福州 350002)
(2: Fuzhou University, Fuzhou 350002, P. R. China)
科学模拟湖泊洪水的形成与演进过程,是湖泊建设规划与实时管理的基础性工作.根据地形、地势和洪水特性,研发适合湖泊自身特点、兼顾精度和效率的洪水演算模型,一直是水利工作者追求的重点.南四湖(34°27′~35°20′N,116°34~117°21′E)为中国第6大淡水湖,湖面面积1266 km2,南北长(约120 km),东西窄(最宽处达25 km,最窄处仅有5~6 km),自上而下由南阳湖、独山湖、昭阳湖和微山湖4个湖泊串联组成,之间无明显分界.南四湖有53条入湖河流,上游的南阳湖受水面积最大,约占南四湖流域面积的63%,而容积则仅占南四湖总容积的17%(水位在37.0 m时),受水面积与库容不相适应.加之芦苇、湖草、庄台等阻水物,洪水发生时南阳湖持续高水位,顶托河道入流,湖滨及湖西地区易出现“洪水不能入湖,坡水不能入河,汛期河湖水位壅高不下”的现象;独山湖、昭阳湖及微山湖亦在不同程度上存在这一现象.入流众多、地形复杂的特点,造成科学模拟南四湖洪水存在较大的困难:既不能概化成单个“水库”,又不能概化为“河道”. 1960s在湖腰处建设二级坝,在水力联系上将南四湖分成了上、下两个湖泊,从表面上看将南四湖概化为两个“串联水库”似乎可行,但在汛期时(尤其是大水年),上、下湖水位差超过3 m,洪水演算误差极大.更遑论将其视为一个“水库”.在该背景下,1960s老一辈水利人创造性地提出了“三湖两河”理念,并建立了基于半图解法的“三湖两河”洪水演算模型[1],该模型长期服务于南四湖的规划建设任务.
半图解法、列表试算法[2]是20世纪最常用的水库调洪演算方法,但随着计算机科学的发展,在计算效率和计算精度上受到新兴数值解法的冲击. 1980s陈守煜[3-4]对水库调洪函数数值解的存在性、唯一性和适定性进行了证明,比较了改进欧拉法、三阶龙格库塔法、四阶龙格库塔法等算法的计算精度,证明了四阶龙格库塔法的优越性,并在多个水库得到成功应用[5]. Fenton[6]于1992年提出了类同于陈守煜的调洪演算数值解法,认为这种解法在求解复杂泄流方式时具有优势,并指出数值解法更为直观,效率和精度更高,全面优于半图解法等传统方法.此外,金菊良等[7]和许永功等[8]建立了基于BP网络的水库调洪演算方法;吴成国等[9]提出了求解水库分期汛限水位的人工神经网络调洪演算方法,实例研究表明其精度可满足实际工程需求.归纳起来,水库调洪演算方法可归为3类:(1)传统方法,例如图解法、半图解法、列表法等;(2)数值解法,目的是求解水库调洪演算微分方程式,以有限差分法最为常见,主要方法有改进欧拉法、三阶龙格库塔法、四阶龙格库塔法等;(3)人工智能方法,例如神经网络等.从模型稳定性、计算精度和实用上角度来看,目前数值解法应用最为广泛,其中又以四阶龙格库塔法为优秀代表.
南四湖“三湖两河”模型,3个湖泊之间没有实际泄洪建筑物,各湖泊的水位和流量是相互影响的.半图解法存在大量插值计算,特别是在高水位时产生较大误差,并会向相邻湖区传递扩散;采用有限差分形式的数值解法,不用插值,较传统方法无论是计算精度还是计算效率都明显进步,在串联型湖泊调洪演算中优势突出.水文学中河道洪水演算以马斯京根法为代表[10],自1969年Cunge[11]提出了改进的马斯京根法之后,发展迅速并在河道洪水演算中得到了广泛应用[12-16].然而,马斯京根法主要适用于运动波,南四湖湖盆浅平、比降不大,再加上该法难以求解相邻湖泊的水位—流量关系,因此在“三湖两河”模型的河道洪水演算中难以直接采用,遂采用具备上述应用条件的动力学方法[17-18]对“两河”水流进行演算.另外,南四湖最宽处达25 km,部分湖区为死水区,完全视其为河道,采用一维水动力学法显然难以较好地模拟其实际情况[19].若采用二维水动力学法,南四湖湖区面积高达1266 km2,高精度地形资料获取困难,计算效率低,不具备时效性和预报的实用性,在二维空间里难以模拟二级坝(内边界条件)的过流情况,限制了该法在南四湖的应用.显然由于南四湖独特的地形地势条件,纯动力学方法并未能优于水文学(“三湖”)与水动力学(“两河”)结合的方法.为此,本文遵循继承“三湖两河”理念,建立基于四阶龙格库塔法的南四湖“三湖两河”调洪演算模型,称之为南四湖“三湖两河”调洪演算数值解模型,对传统基于半图解法的南四湖洪水演进模型进行革命性改进;并对模型中的若干经验参数进行敏感性分析,力图为南四湖洪水管理提供支撑工具,为类似湖泊提供借鉴和参考.
1 南四湖“三湖两河”洪水演进模型原理 1.1 模型假定“三湖两河”模型是根据南四湖地形、地势、洪水与水面特性,将其概化为“三湖”和“两河”来模拟洪水的工具. “三湖”即南阳湖、独昭湖(独山湖与昭阳湖的合并)和微山湖3个水平湖;把连接南阳湖和独昭湖、独昭湖和微山湖间的窄浅段视为河道,即为“两河”. “三湖”与“两河”的范围与代表站如下:中泓线里程桩号0~12 K为南阳湖,以王堰站(12 K)代表平均水位;桩号12~34 K为河道1;桩号34~42 K为独昭湖,以石口站(42 K)代表平均水位;桩号42~94 K为河道2;桩号94~120 K为微山湖,以微山站(94 K)代表平均水位(图 1).此外,在“不考虑河道调蓄作用,将河道的容积纳入相邻湖泊计算”的状态下,“三湖”的分界线则是:南阳湖与独昭湖以南阳镇为界(24 K),南阳镇以北为南阳湖,以南为独昭湖;二级坝(66 K)则为独昭湖与微山湖的分界.
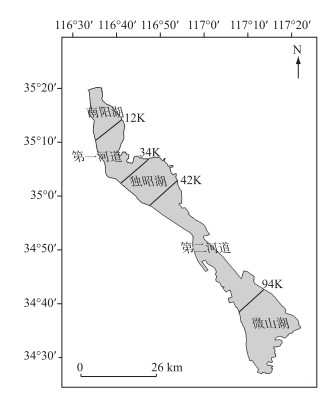
|
图 1 南四湖“三湖两河”示意图 Fig.1 Schematic diagram of "three-lake and two-river" in the Nansi Lake |
“三湖两河”模型假定如下:
1) 将河道的容积纳入相邻湖泊进行计算,不考虑窄浅河道的调蓄作用.
2) 洪水在湖泊和河道中的演进过程,分别用水量平衡方程和动力平衡方程来描述.
3) 通过恒定流计算原理得到上一级湖水位—上一级湖流量—下一级湖水位关系,进而自上而下实现上一级湖到下一级湖的逐级演算.
4) 洪水从南阳湖至独昭湖的传播历时6 h,独昭湖至微山湖历时12 h.
5) 南四湖出口韩庄闸具有固定的水位—流量关系(不受廻水影响).
1.2 控制方程 1.2.1 “三湖”洪水演算控制方程湖泊洪水调节计算是南四湖“三湖两河”洪水演算模型的核心,控制方程为水量平衡方程[1]:
| $ \frac{{{I_1} + {I_2}}}{2} \cdot t - \frac{{{D_1} + {D_2}}}{2} \cdot t = {V_2} - {V_1} $ | (1) |
式中,I1和I2分别为时段1和时段2的进湖流量(m3/s),D1和D2分别为时段1和时段2的出湖流量(m3/s),V1和V2分别为时段1和时段2的湖泊容积(m3),t为时间步长(s).将公式(1)分别应用于南阳湖、独昭湖及微山湖,可推得各个湖泊的洪水调节计算公式:
| $ \frac{{{I_{{{\rm{a}}_1}}} + {I_{{{\rm{a}}_2}}}}}{2} \cdot t - \frac{{{D_{{{\rm{a}}_1}}} + {D_{{{\rm{a}}_2}}}}}{2} \cdot t = {V_{{{\rm{a}}_2}}} - {V_{{{\rm{a}}_1}}} $ | (2) |
| $ \frac{{{I_{{{\rm{b}}_1}}} + {I_{{{\rm{b}}_2}}}}}{2} \cdot t + \frac{{{D_{{{\rm{a}}_1}}} + {D_{{{\rm{a}}_2}}}}}{2} \cdot t - \frac{{{D_{{{\rm{b}}_1}}} + {D_{{{\rm{b}}_2}}}}}{2} \cdot t = {V_{{{\rm{b}}_2}}} - {V_{{{\rm{b}}_1}}} $ | (3) |
| $ \frac{{{I_{{{\rm{c}}_1}}} + {I_{{{\rm{c}}_2}}}}}{2} \cdot t + \frac{{{D_{{{\rm{b}}_1}}} + {D_{{{\rm{b}}_2}}}}}{2} \cdot t - \frac{{{D_{{{\rm{c}}_1}}} + {D_{{{\rm{c}}_2}}}}}{2} \cdot t = {V_{{{\rm{c}}_2}}} - {V_{{{\rm{c}}_1}}} $ | (4) |
式中,a、b和c分别为南阳湖、独昭湖和微山湖,记为A湖、B湖和C湖;Ia1、Ib1和Ic1分别为时段1 A湖、B湖和C湖的进湖流量(m3/s);Ia2、Ib2和Ic2分别为时段2各湖进湖流量(m3/s);Da1、Db1和Dc1分别为时段1各湖出湖流量(m3/s);Da2、Db2和Dc2分别为时段2各湖出湖流量(m3/s);Va1、Vb1和Vc1分别为时段1各湖容积(万m3);Va2、Vb2和Vc2分别为时段2各湖容积(万m3);式(3)中的Da1和Da2分别为时段1、时段2南阳湖前6 h出湖流量(m3/s);式(4)中的Db1和Db2分别为时段1及时段2独昭湖前12 h的出湖流量(m3/s).
将式(2~4)中的已知项移至右端,整理后分别变成:
| $ \frac{{2{V_{{{\rm{a}}_2}}}}}{t} + {D_{{{\rm{a}}_2}}} = {I_{{{\rm{a}}_1}}} + {I_{{{\rm{a}}_2}}} + \left( {\frac{{2{V_{{{\rm{a}}_1}}}}}{t} + {D_{{{\rm{a}}_1}}}} \right) - 2{D_{{{\rm{a}}_1}}} $ | (5) |
| $ \frac{{2{V_{{{\rm{b}}_2}}}}}{t} + {D_{{{\rm{b}}_2}}} = {D_{{{\rm{a}}_1}}} + {D_{{{\rm{a}}_2}}} + {I_{{{\rm{b}}_1}}} + {I_{{{\rm{b}}_2}}} + \left( {\frac{{2{V_{{{\rm{b}}_1}}}}}{t} + {D_{{{\rm{b}}_1}}}} \right) - 2{D_{{{\rm{b}}_1}}} $ | (6) |
| $ \frac{{2{V_{{{\rm{c}}_2}}}}}{t} + {D_{{{\rm{c}}_2}}} = {D_{{{\rm{b}}_1}}} + {D_{{{\rm{b}}_2}}} + {I_{{{\rm{c}}_1}}} + {I_{{{\rm{c}}_2}}} + \left( {\frac{{2{V_{{{\rm{c}}_1}}}}}{t} + {D_{{{\rm{c}}_1}}}} \right) - 2{D_{{{\rm{c}}_1}}} $ | (7) |
式(5)~(7)即为“三湖两河”模型中“三湖”洪水演进的控制性方程.在修正洪水入流过程之后,基于以上公式,辅以通过天然河道的恒定流水面线计算原理得到上级湖水位—上级湖流量—下级湖水位关系,形成洪水演算分析的辅助曲线,进而推得南四湖洪水期内的水位和流量过程.
1.2.2 “两河”洪水演进控制方程对连接“三湖”的两条“窄浅河道”,采用河道恒定流的水面曲线计算原理进行洪水演进计算[1],控制方程为:
| $ {z_1} + \frac{{{\alpha _1} \cdot v_1^2}}{{2g}} = {z_2} + \frac{{{\alpha _2} \cdot v_2^2}}{{2g}} + \Delta {h_f} + \Delta {h_j} $ | (8) |
式中,z1、z2分别为相邻断面1、2的水位(m);v1、v2分别为相邻断面1、2的流速(m/s);α1、α2分别为相邻断面1、2的动量校正系数;g为重力加速度(m2/s);Δhf为沿程水头损失(m);Δhj为局部水头损失(m).将式(8)推广至复式断面,根据湖泊形状的特性,忽略相邻断面的流速水头差及局部水头损失,可得到衔接“三湖”水位—流量关系的计算公式:
| $ {z_1} - {z_2} = \frac{{{Q^2} \cdot \Delta l}}{{\overline {{K_2}} }} $ | (9) |
式中,Q为河道过流量(m3/s);Δl为相邻断面1、2间的河道长度,一般取值2~4 km;
入湖洪水过程处理是“三湖两河”模型的重要组成部分.依据南四湖流域的特点,设计洪水计算时将南四湖的入湖洪水过程概化为14个分区,其中湖西包括梁济运河、洙赵新河、万福河、东鱼河、复兴河和丰沛地区6个分区;湖东有洸府河、泗河、白马河、城郭河和十字河5个分区,以及湖面南阳湖、独昭湖和微山湖3个分区.湖西地区为黄泛平原,由设计暴雨推求设计洪水;湖东地区由流量直接推求设计洪水,湖面则采用降雨量扣除蒸发量的方法实现对洪量的推求.以1957年的洪水过程为典型年,求得14条理想入湖过程线,洪水历时30 d.理想设计入湖洪水过程线需经滨湖来水处理、河道安全泄流削峰处理以及湖内洪水顶托处理之后,方能代入调洪演算模型进行计算.
1) 滨湖来水处理:南四湖滨湖范围内,高程37.0 m以下的面积(废黄河高程系,下同)约3000 km2,由于地势低洼,无法自排入湖.因此,需先扣除这部分区域的洪水,之后根据滨湖地区排灌站现状,加上这部分区域的提排量,便是滨湖来水.以上扣除的滨湖地区来水,若本时段内无法完全提排入湖,剩余部分则在随后的时段内提排入湖.滨湖来水流量的扣除,以南四湖流域各个分区的滨湖面积与各个分区的总面积之比,再乘以30 d理想入湖流量得到.南四湖流域11个分区的滨湖面积与总面积统计结果见表 1.
| 表 1 各分区总面积及滨湖面积(km2) Tab.1 Total area of each subarea and their waterfront area (km2) |
2) 河道安全泄流削峰处理:设计时规定滨湖地区的排水模数q=0.4 m3/(s·km2),各湖最大提排流量为排水模数与各湖滨湖面积之积.提排入湖流量与湖泊水位关系密切,当水位高于38.0 m时,排灌站无法提排滨湖来水入湖;水位高于37.0 m而低于38.0 m时,最多仅能提排最大提排流量的一半;而水位低于37.0 m时,可按提排能力提排流量入湖.再者,各河道入湖洪水均受河道安全泄量的控制,各河最大入湖流量见表 2.若时段内入湖流量大于表 2规定的最大入湖流量,做削峰处理,被削去的流量随后入湖.
| 表 2 南四湖各主要河道安全过流量(m3/s) Tab.2 Safety discharge of major rivers in the Nansi Lake (m3/s) |
3) 洪水顶托处理:指湖内达到一定的高水位时,入湖洪水受到了湖内洪水的顶托,需对理想入湖洪水过程进行折减.入南阳湖的梁济运河、洸府河、泗河、洙赵运河、万福河及白马河在湖水位高于35.8 m时开始折减;入独昭湖的东鱼河、复兴河及城郭河在湖水位高于36.0 m时开始折减;入微山湖的丰沛地区与十字河在湖水位高于36.2 m时开始折减.各湖不同水位折减系数如图 2所示.
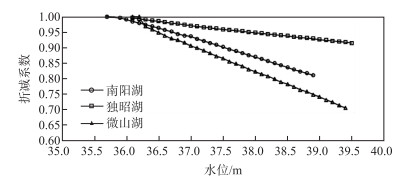
|
图 2 各湖不同水位折减系数 Fig.2 Reduction factor of different water levels in these lakes |
经过上述处理,河流实际入湖洪水过程可由式(10)表示:
| $ {Q_{{\rm{real}}}} = \min \left( {\left( {{Q_{{\rm{ideal}}}} - {Q_{{\rm{side}}}}} \right),{Q_{{\rm{safe}}}}} \right)\alpha + {Q_{{\rm{pumping}}}} $ | (10) |
式中,Qreal为实际入湖洪水过程,Qideal为理想设计洪水过程,Qside为滨湖低洼地区不能自排入湖的洪水,Qsafe为超过河道安全泄量的洪水,α值为受湖内洪水顶托影响的折减系数,Qpumping则为滨湖低洼地区的提排流量.在进行调洪演算时,除了经过上述处理的11条河流(南阳湖6个片区,独昭湖3个片区,微山湖2个片区)实际入湖洪水外,还要加上3片湖面入流.
1.3.2 河道糙率南四湖湖内情况错综复杂,湖内断面大多为复式断面,分为深槽、明湖、湖草及芦苇4种类型[1].根据南四湖实测地形断面资料、引水测验调查及水位条件,综合确定糙率(表 3).
| 表 3 南四湖各种类型糙率计算公式 Tab.3 Calculation formula of various types of roughness coefficient in the Nansi Lake |
获得糙率值后,对于南阳湖与独昭湖间的连接河道(12~34 K),假定河道末断面(34 K)水位值(代表独昭湖水位Hdz)及一系列流量值,通过公式(10)可计算得到南阳湖某一出湖流量Dny、独昭湖某一水位条件下相邻河道的断面水位,并逐步向上游演算得到河道首断面(12 K)的水位值(代表南阳湖水位Hny).至此,得到了南阳湖水位—南阳湖流量—独昭湖水位(Hny—Dny—Hdz)的关系.同理,对于独昭湖与微山湖间的连接河道(42~94 K),假定河道末断面(94 K)水位值(代表微山湖水位Hws)及一系列流量值,通过公式(9)可计算得到独昭湖某一出湖流量、微山湖某一水位条件下相邻河道的断面水位,并逐步向上游演算得到河道首断面(42 K)的水位值(代表独昭湖水位Hdz).有所不同的是,独昭湖与微山湖连接河道间建有二级坝,在不同过流条件下,闸上(66 K)与闸下(67 K)水位的关系见表 4.
| 表 4 不同过流条件下二级坝闸上—闸下水位(m) Tab.4 Stage relation in secondary dam upstream and downstream with different discharge condition |
至此,得到了独昭湖水位—独昭湖流量—微山湖水位(Hdz—Ddz—Hws)的关系.此外,根据韩庄闸的调度规则,微山湖出口(亦即南四湖出口)韩庄闸具有固定的水位—泄量关系(Hws—Dws).
2 基于四阶龙格库塔法的南四湖“三湖两河”洪水演进模型求解 2.1 算法原理湖泊(水库)调洪演算的原理是解下列方程:
| $ Q\left( t \right) - q\left( z \right) = \frac{{{\rm{d}}V}}{{{\rm{d}}t}} $ | (11) |
式中,t为时间;Q(t)为入湖(库)洪水流量过程,是时间t的函数;z表示水位;q(z)为湖泊(水库)泄流量,是水位z的函数;V为湖泊(水库)的蓄水量.式(11)可写成:
| $ \frac{{{\rm{d}}z}}{{{\rm{d}}t}} = \frac{{Q\left( t \right) - q\left( z \right)}}{{F\left( z \right)}} $ | (12) |
式中,F(z)为湖泊(水库)表面积,是水位z的函数.然而,有些时候只有水位—库容关系,而没有水位—面积曲线(本文收集南四湖资料时,便缺失了水位—面积曲线).此时倒推一步有:
| $ Q\left( t \right) - q\left( z \right) = \frac{{{\rm{d}}V}}{{{\rm{d}}t}} = \frac{{{\rm{d}}V}}{{{\rm{d}}t}} \cdot \frac{{{\rm{d}}z}}{{{\rm{d}}t}} $ | (13) |
| $ \frac{{{\rm{d}}z}}{{{\rm{d}}t}} = \frac{{Q\left( t \right) - q\left( z \right)}}{{{\rm{d}}V/{\rm{d}}z}} $ | (14) |
式(14)可归结为求解一阶微分方程z′(t)=f(t, z)满足初始条件z(t0)=z0时的函数解z(t),即求解湖泊(水库)水位在系列时刻t上的近似值. Q(t)为各湖实际入湖洪水过程.对于q(z),微山湖和南阳湖、独昭湖有所不同.微山湖位于南四湖的下游处,微山湖的出口即是南四湖的出口,南四湖的出口韩庄闸有固定的水位—流量关系.而对于南阳湖和独昭湖,实质上它们是人为划定的,出口断面并没有实际的泄流建筑物,无法直接获取它们的蓄泄曲线.因此,通过“两河”(三湖之间的连接河道)的恒定流水面曲线原理推算水位流量关系,详见1.3.3节.求得Hdz—Ddz—Hws与Hny—Dny—Hdz的关系.湖泊调洪演算过程中,由于微山湖的蓄泄关系q(z)已知,先对微山湖进行洪水调节计算,得到微山湖的水位和流量.此后,可视微山湖水位为一常数,利用Hdz—Ddz—Hws求得独昭湖的q(z);同理,视独昭湖水位为一常数,利用Hny—Dny—Hdz关系求得南阳湖的q(z). dV/dz为库容水位关系V=f(z)的一阶导数,仍用F(z)表示.
洪水调节计算开始时(t=t0),初始水位z0为湖泊(水库)的汛限水位,南阳湖及独昭湖为34.2 m,微山湖则为32.5 m.应用四阶龙格库塔公式可得:
| $ {z_i} = {z_{i - 1}} + \left( {{k_1} + 2{k_2} + 2{k_3} + {k_4}} \right)/6 $ | (15) |
式中:
| $ {k_1} = \Delta t\left[ {Q\left( {{t_{i - 1}}} \right) - q\left( {{z_{i - 1}}} \right)} \right]/F\left( {{z_{i - 1}}} \right) $ | (16) |
| $ {k_2} = \Delta t\left[ {Q\left( {{t_{i - 1}} + \Delta t/2} \right) - q\left( {{z_{i - 1}} + {k_1}/2} \right)} \right]/F\left( {{z_{i - 1}} + {k_1}/2} \right) $ | (17) |
| $ {k_3} = \Delta t\left[ {Q\left( {{t_{i - 1}} + \Delta t/2} \right) - q\left( {{z_{i - 1}} + {k_2}/2} \right)} \right]/F\left( {{z_{i - 1}} + {k_2}/2} \right) $ | (18) |
| $ {k_4} = \Delta t\left[ {Q\left( {{t_{i - 1}} + \Delta t} \right) - q\left( {{z_{i - 1}} + {k_3}} \right)} \right]/F\left( {{z_{i - 1}} + {k_3}} \right) $ | (19) |
首先,从微山湖开始进行洪水调节计算.对于公式(14),微山湖的入流包括两部分:一部分是由独昭湖入流的(历时12 h到达微山湖);另一部分则是天然河道及湖面入流,经由入流洪水过程修正之后,两部分叠加,便是公式(14)中的Q(t).微山湖出口(亦即南四湖出口)具有固定的水位—泄量关系(Hws—Dws),对于微山湖某一水位(前一时段),可以推求得相应的q(z).水位—库容关系已知,可推得微山湖不同水位下的dV/dz.因此,可基于四阶龙格库塔法的调洪数值解求得微山湖水位的增量Δh和微山湖下一时段的水位值,进而根据水位—泄量关系求得微山湖下一时段的出流量Dws.微山湖的起调水位为汛限水位32.5 m,独昭湖初始入湖流量为0.
其次,对临近微山湖的独昭湖进行洪水调节计算.同理,独昭湖的入流包括两部分,一部分是由南阳湖入流的(历时6 h到达独昭湖),另一部分则是天然河道及湖面入流,经入流洪水过程修正之后,两部分叠加,便是Q(t).根据Hdz—Ddz—Hws关系,下一时段的Hws前已求得,对于某一独昭湖水位(前一时段),可推求出相应的q(z).水位—库容关系已知,可推得独昭湖不同水位下的dV/dz.至此,基于四阶龙格库塔法的调洪数值解求得独昭湖水位的增量Δh和独昭湖下一时段的水位值Hdz,进而根据Hdz—Ddz—Hws关系求得独昭湖下一时段的出流量Ddz.独昭湖的起调水位为汛限水位34.2 m,南阳湖初始入流量为0.
最后,对南阳湖进行洪水调节计算.此时南阳湖的入流仅有天然河道及湖面入流,经入流洪水过程修正后,便为Q(t).根据Hny—Dny—Hdz关系,下一时段的Hdz前已求得,对于某一南阳湖水位(前一时段),可推求出相应的q(z).水位—库容关系已知,可推得南阳湖不同水位下的dV/dz.至此,基于四阶龙格库塔法的调洪数值解求得南阳湖水位的增量Δh和南阳湖湖下一时段的水位值Hny,进而根据Hny—Dny—Hdz关系求得南阳湖下一时段的出流量Dny.南阳湖的起调水位为汛限水位34.2 m.
下一时段的起调水位便是上一时段求得的水位.重复以上步骤即能求得各个湖泊、各个时段的水位及出湖流量,完成“三湖”的洪水调节计算,具体流程详见图 3.
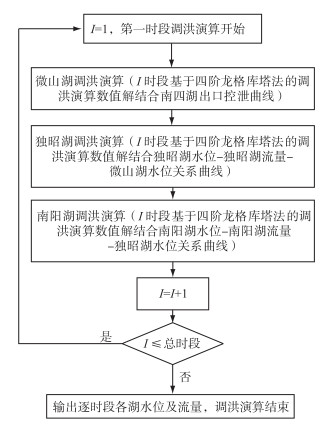
|
图 3 南四湖“三湖两河”洪水演算流程 Fig.3 Flood routing process of "three-lake and two-river" in the Nansi Lake |
选择50年一遇洪水过程[20](本研究有且仅能获取的洪水过程),通过与基于半图解法的“三湖两河”模型进行对比,说明改进模型的合理性和有效性.
水位是洪水调节计算中最为敏感的特征指标. 图 4对比了南阳湖、独昭湖和微山湖两种方法的计算结果,最大水位差绝对值分别为0.14、0.05和0.03 m,总体上均在合理的误差范围内.
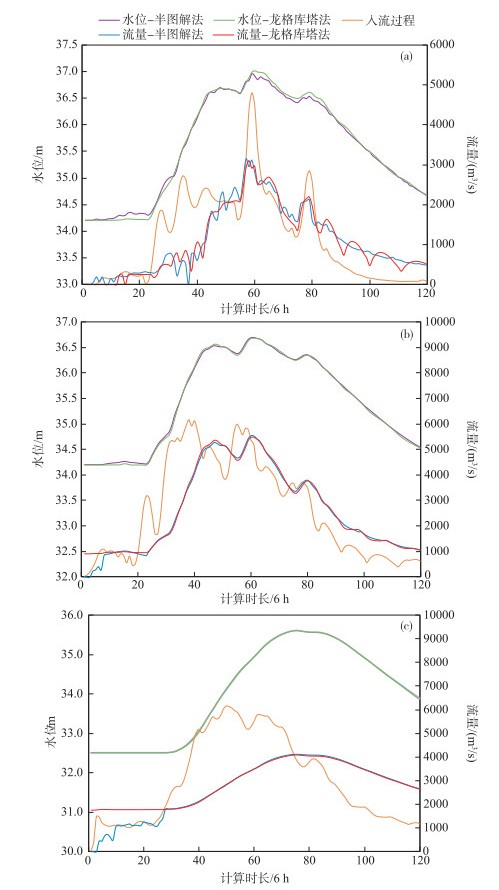
|
图 4 不同解法下南阳湖(a)、独昭湖(b)和微山湖(c)结果对比 Fig.4 Result comparison of Nanyang Lake (a), Duzhao Lake (b) and Weishan Lake (c) using different methods |
对于南阳湖,半图解法和数值解法相差较大(图 4a).
从局部水位差距进行分析,主要不同在于初始时段附近和峰值时段附近.从南阳湖入流过程来看,初始时段入流流量极小(200 m3/s左右),结合南阳湖的出流能力,南阳湖的水位基本不会上升,正如数值解法的水位过程和表 5所示.而半图解法在这种小流量入流的情况下,水位最高上涨了0.11 m,显然是不合理的.在峰值时段附近,数值解法所得水位过程对比半图解法所得水位过程平滑许多,这正是数值解法优化算法的体现,半图解法在峰值之后出现急跌再急升,对比入流曲线,笔者认为是不会出现这样的水位过程的.而数值解法则是峰值后一直缓慢变化,显然能更真实地反映水位过程.
| 表 5 南阳湖初始时段(6~20时段)的入流与出流流量 Tab.5 Inflow and outflow comparison in the initial period of Nanyang Lake (from 6 to 20) |
从独昭湖和微山湖所得结果分析,两种方法逐时刻水位过程及流量过程总体吻合(图 4b、图 4c).不同于半图解法计算受公式(5~7)控制,数值解法的出流流量初值为一固定值,这是因为我们设定计算水位低于起调水位时,保持水位为起调水位,微山湖出口韩庄闸具有固定水位—流量关系,因此出流流量初值为起调水位对应的固定值.独昭湖亦是同理.出流流量初值的不同是由于计算方法的差异导致的,然而初值求解的瑕疵并未引起流量过程和水位过程的波动,证明了数值解法的稳定性.相比传统的半图解法,以上分析验证了基于四阶龙格库塔法的调洪数值解法的适用性和合理性.
从计算效率方面分析,由于洪水过程仅有120个时段,CPU运行时间均近似为0.然而,从上述算法原理分析,数值解法较半图解法具有无需进行插值、存储量小的优点,对于日后长时段、精细时段的洪水过程计算,能明显缩短计算时间,提高洪水调节计算分析的效率.
综上所述,基于四阶龙格库塔法的南四湖“三湖两河”洪水调算模型优于基于半图解法的南四湖“三湖两河”洪水调算模型.
3.2 敏感性分析基于四阶龙格库塔法的南四湖“三湖两河”模型,对排水模数、“两河”传播历时和韩庄闸水位流量关系等模型经验参数进行敏感性分析,以探索这些参数变化对南四湖水位过程以及防洪工程建设的影响.
3.2.1 排水模数前已述及,南四湖滨湖范围内,高程37.0 m以下的面积约3000 km2,因地势低洼洪水无法自排入湖,须经机电排灌站提排入湖.滨湖地区的当前排水模数q=0.4 m3/(s·km2).随着南四湖机电排灌站建设的完善,滨湖地区排水模数势必会增大.此外,排灌站受淹的突发情况也会导致排水模数q变小.因此,取排水模数q=0、0.1、0.2、0.3、0.4(当前排水模数)、0.5、0.6 m3/(s·km2)进行分析,以探究排水模数变化对各湖泊水位过程的影响.计算结果如图 5所示.
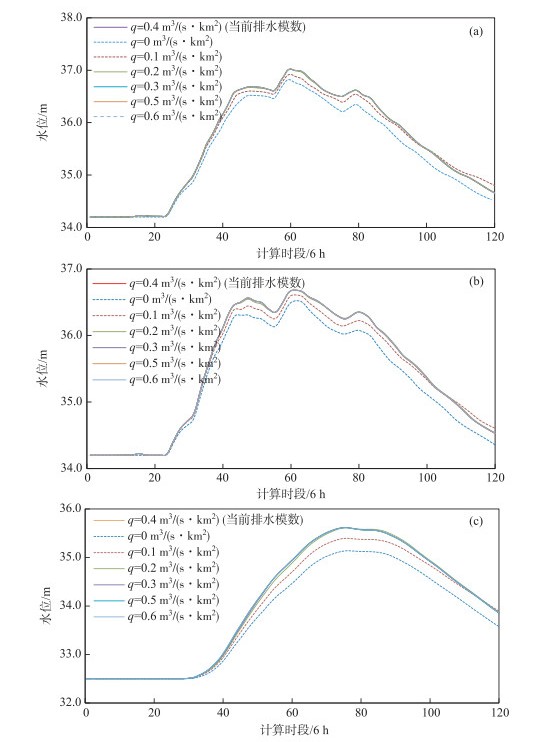
|
图 5 不同排水模数下南阳湖(a)、独昭湖(b)和微山湖(c)结果对比 Fig.5 Result comparison of Nanyang Lake (a), Duzhao Lake (b) and Weishan Lake (c) under different drainage modulus |
结果表明,与排水模数q > 0.2 m3/(s·km2)时,南阳湖、独昭湖以及微山湖的水位过程基本保持不变.这说明当前情况下,单纯地提高滨湖地区洪水的提排能力,并不能有效地减少涝灾面积,提排滨湖洪水入湖.另外,排水模数q=0和0.1 m3/(s·km2)时,各湖的水位出现明显的下降,南阳湖的水位峰值分别降低0.20和0.10 m;独昭湖的水位峰值分别降低0.16和0.07 m;微山湖的水位峰值则分别降低达0.46和0.11 m.以上结果说明,滨湖地区的洪水对南四湖的高水位有显著影响,这部分洪水是否提排入湖以及何时提排入湖仍待商榷.笔者认为,两者的关系近似于大坝与下游防洪对象的关系,却又有所不同.类似的地方在于,刚开始来水时有多少提排多少入湖,湖泊到一定高水位时,则限制提排入湖流量,正如大坝控制安全泄量一般.不同在于,大坝到达防洪限制水位时则全力泄水保坝,而由于湖泊高水位的顶托,滨湖地区的洪水无法提排入湖,“因洪致涝”势必给滨湖地区带来严重的影响.因此,建议相关防汛部门务必谨慎处理滨湖洪水入湖问题.
3.2.2 韩庄水位—流量关系前述南四湖出口韩庄闸具有固定的水位—流量关系见表 6.
| 表 6 韩庄闸水位—流量关系 Tab.6 Stage-discharge relation of Hanzhuang sluice |
湖泊水位过度抬高常常是出口泄流能力不足导致的.当前水位—流量关系状态下,南阳湖、独昭湖和微山湖水位峰值分别为37.02、36.68和35.62 m(图 6中流量系数为1.0对应的水位峰值).现保持各水位值不变,对出流流量进行折减或放大,分析不同水位—流量对应关系条件下各湖水位峰值的变化情况(图 6).
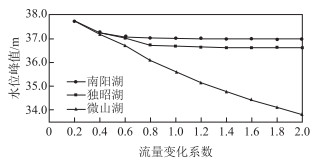
|
图 6 韩庄闸泄流量变化对各湖水位峰值的影响 Fig.6 Effect on the peak value of water level with changes of discharge of Hanzhuang sluice |
图 6表明,增大出口泄流能力,可显著降低微山湖水位峰值,如增大至1.2倍出湖流量,水位峰值由35.62 m降至35.17 m,降幅达0.45 m.因此,对于单个水平湖或者水库增强出口的泄流能力对水位峰值的调控作用明显.然而,泄流能力放大至两倍,独昭湖及微山湖的水位峰值仍变化微小,独昭湖由36.68 m降至36.63 m,微山湖由37.02 m降至36.99 m.复杂的入流情况和独特的地形构造为主因.南阳湖及微山湖承揽了南四湖流域多达87%的汇水,水位主要受入流影响.独昭湖与微山湖间的“连接河道”窄而长,杂草丛生、部分庄台、高地阻水严重,微山湖水位的下降对独昭湖和南阳湖影响有限.因此,对50年一遇及以下设计洪水,单纯扩大韩庄闸的泄流能力对降低南四湖高水位作用不大.南四湖的防洪工程具有整体性,在对排水模数的讨论中,我们也发现单纯地提高滨湖地区洪水的提排能力,并不能有效地减少滨湖地区的涝灾面积,因为湖内到达一定的高水位时洪水便很难提排入湖.基于此,建议在实施以上措施的同时,配合实施“连接河道”浅槽工程,打通南阳镇东西的阻水卡口,使泗河、洸府河和洙赵新河等河道的来水尽快进入独昭湖深水区,疏通独昭湖至微山湖间的浅滩湖段,使下泄的洪水快速通过浅滩湖段而进入微山湖深水区,进而有效降低南阳湖及独昭湖的高水位,减轻南四湖的防洪压力.
另外,对出流流量进行折减分析发现,折减系数越小,各湖水位越高,各湖的水位越是接近,从侧面验证了本模型的合理性.
3.2.3 传播历时本模型假定洪水从南阳湖至独昭湖的传播历时为6 h,独昭湖至微山湖12 h,当前还缺乏论证.按“连接河道”的中泓线里程计算,南阳湖至独昭湖约22 km,独昭湖至微山湖约52 km,后者距离是前者的2~3倍.若以模型假定的传播时间计算,水流平均流速在1~1.2 m3/s之间.南四湖湖盆浅平,更类似平原河道,一般较难达到这个速度水平.现对洪水不同传播历时组合进行分析,以探求湖泊间洪水传播历时对不同湖水位峰值与峰现时间的影响.不同组合方案计算结果如表 7所示.
| 表 7 各湖泊间“河道”传播历时对各湖水位峰值及峰值出现时间的影响* Tab.7 The effect of propagation time between adjacent lake on peak value of water level and corresponding appearance time |
随着传播历时的增加、水流平均流速减小(最低0.25 m3/s),各湖水位峰值与峰现时间均有所变化,水位峰值最多降低9~12 cm(表 7).究其原因,传播历时的增长,降低了大洪峰形成的几率,进而降低了各湖的水位峰值.南阳湖的水位峰值提前一个时段出现,独昭湖及微山湖最多分别推后3和11个时段出现.可见“连接河道”的传播历时对各湖的水位过程预测颇有影响,建议日后防汛工作中增强对不同来水情况下“连接河道”的监测,有条件的情况下进行模型试验,以确定各湖间的传播时间,更好地服务于南四湖的规划建设.
4 结论阐述了南四湖“三湖两河”洪水演进模型产生背景、原理、入流过程处理等方面,采用四阶龙格库塔数值解法,代替传统的半图解法对模型进行改进完善,提出了基于四阶龙格库塔法的南四湖“三湖两河”洪水调算模型;选择50年一遇设计洪水过程,从水位过程平滑性、初值时段和峰值时段附近水位合理性等方面论证了基于四阶龙格库塔法的南四湖“三湖两河”洪水调算模型的适用性和合理性,证明了较之传统的半图解法,数值解法在计算精度和计算效率上的优越性,能科学高效模拟南四湖洪水的演进过程.
分析排水模数、“两河”传播历时等经验值及韩庄闸水位—流量关系对各湖水位过程及水位峰值的影响,提出了对南四湖未来防洪工程、排涝工程等建设具有重要指导意义的结论:
1) 单纯地提高滨湖地区洪水的提排能力及扩大韩庄闸的泄流能力难以有效地降低南四湖的高水位、减少滨湖地区的涝灾面积,建议实施南四湖湖内浅槽工程,对南阳湖与独昭湖、独昭湖与微山湖间的窄浅河道进行疏通,提高洪水的快速下泄能力,再配合上述防洪工程措施,可有效降低南阳湖、独昭湖的高水位及滨湖地区的受淹面积,进而减轻南四湖的防洪压力.
2) 过低的洪水提排能力,“因洪致涝”势必给滨湖地区带来严重的影响,防汛部门应准确把握二者的利弊关系.
3) “两河”的传播历时对各湖的水位峰值颇有影响,在南四湖未来的规划建设中应重点予以确定.
需要指出的是:①除了以上讨论的排涝模数、“两河”传播历时外,模型还有多个经验参数,如洪水顶托折减系数、滨湖洪水入湖受限水位、河道糙率等,在实际应用中具有很高的复杂性和不确定性.然而,这些人为设定的参数亦正是老一辈水利人辛勤劳动和智慧的结晶,这也是我们坚持对“三湖两河”模型进行不断完善改进,而不是弃用的主要原因,即使是发展快速的水动力学模型也很难处理这些宝贵的经验方法. ②本文对南四湖“三湖两河”调洪演算模型的改进是局部的,今后将基于四阶龙格库塔法的南四湖“三湖两河”模型,展开如下工作:采用一维非恒定流对“三湖两河”里的“两河”进行水动力学演算,以较好地考虑河道的调蓄能力;建立整个南四湖流域的分布式水文模型,为南四湖“三湖两河”模型提供动态边界条件,实现流域降雨—径流洪水—湖内水文过程演进的实时预报.
| [1] |
Shandong Survey and Design Institute of Water Conservancy ed. Discussion of flood calculation method of the Nansi lake (exposure draft). Jinan:Shandong Survey and Design Institute of Water Conservancy, 1976. [山东省水利勘测设计院. 南四湖洪水计算方法商榷(征求意见稿). 济南: 山东省水利勘测设计院, 1976. ]
|
| [2] |
Zhou ZH. The water conservancy and hydropower planning. Beijing: China Water & Power Press, 1997. [周之豪. 水利水能规划. 北京: 中国水利水电出版社, 1997.]
|
| [3] |
Chen SY. The numerical analysis of reservoir flood regulation and the corresponding program. Journal of Hydraulic Engineering, 1980(2): 46-51. [陈守煜. 水库调洪计算的数值解法及其程序. 水利学报, 1980(2): 46-51.] |
| [4] |
Chen SY. The theory, model and program(TI-58C, 58, 59) of numerical analysis of reservoir flood regulation. Journal of Chongqing Jiaotong University:Natural Science, 1983(1): 64-73. [陈守煜. 水库调洪数值解法的理论、模式与程序(TI-58C、58、59). 重庆交通大学学报:自然科学版, 1983(1): 64-73.] |
| [5] |
Chen SY. Numerical and analytical solution method for reservoir routing. Journal of Dalian University of Technology, 1996, 36(6): 721-724. [陈守煜. 水库调洪数值-解析解法. 大连理工大学学报, 1996, 36(6): 721-724.] |
| [6] |
Fenton JD. Reservoir routing. Hydrological Sciences Journal/Journal Des Sciences Hydrologiques, 1992, 37(3): 233-246. DOI:10.1080/02626669209492584 |
| [7] |
Jin JL, Wei YM, Yang XH et al. Neural network and its application to calculation of reservoir flood. Journal of Catastrophology, 1997, 12(4): 1-5. [金菊良, 魏一鸣, 杨晓华等. 神经网络及其在水库调洪演算中的应用. 灾害学, 1997, 12(4): 1-5.] |
| [8] |
Xu YG, Li SL, Zhu L et al. Establishment and application of the BP neural network model on flood routing through reservoir. Jour of Northwest Sci-Tech Univ of Agri and For Nat Sci Ed, 2001, 29(5): 134-136. [许永功, 李书琴, 朱林等. 水库调洪演算BP网络模型的建立与研究. 西北农林科技大学学报:自然科学版, 2001, 29(5): 134-136.] |
| [9] |
Wu CG, Jin JL, Zhou YL et al. Application of neural networks to determine limited water level of reservoir flood routing. Journal of Applied Sciences, 2009, 27(3): 288-293. [吴成国, 金菊良, 周玉良等. 确定水库分期汛限水位的神经网络调洪演算方法. 应用科学学报, 2009, 27(3): 288-293.] |
| [10] |
Huang GR, Rui XF. Radial basis function-neural network model for channel flood routing. Journal of Hohai University:Natural Sciences, 2003, 31(6): 621-625. [黄国如, 芮孝芳. 河道洪水演算的径向基函数神经网络模型. 河海大学学报:自然科学版, 2003, 31(6): 621-625.] |
| [11] |
Gunge JA. On the subject of a flood propagation method (Muskingum method). J of Hydraul Res, 1969, 7(2): 205-230. DOI:10.1080/00221686909500264 |
| [12] |
Rui XF. Numerical diffusion of kinematic wave and flood routing method. Journal of Hydraulic Engineering, 1987(2): 39-45. [芮孝芳. 运动波数值扩散与洪水演算方法. 水利学报, 1987(2): 39-45.] |
| [13] |
Li ZJ. Research on channel routing method with flood diversion and flood retarding areas. Advances in Water Science, 1997, 8(1): 65-70. [李致家. 具有行蓄洪区的河道流量演算方法探讨. 水科学进展, 1997, 8(1): 65-70.] |
| [14] |
Leon JG, Calmant S, Seyler F et al. Rating curves and estimation of average water depth at the upper Negro River based on satellite altimeter data and modeled discharges. Journal of Hydrology, 2006, 328(3/4): 481-496. |
| [15] |
Wang ZZ, Cheng L, Wang YT et al. Modelling the flood behavior in a river network considering the streambed infiltration and its application in Haihe River basin of China. Journal of Hydraulic Engineering, 2015, 46(4): 414-424. [王宗志, 程亮, 王银堂等. 高强度人类活动作用下考虑河道下渗的河网洪水模拟. 水利学报, 2015, 46(4): 414-424.] |
| [16] |
Yoo C, Lee J, Lee M. Parameter estimation of the Muskingum channel flood-routing model in ungauged channel reaches. Journal of Hydrologic Engineering, 2017, 22(7): 05017005. DOI:10.1061/(ASCE)HE.1943-5584.0001507 |
| [17] |
Tan WY, Hu SY, Wang YT et al. Flow modelling of the middle Yangtze river-dongting lake flood control system-Ⅰ. Modelling procedures and basic algorithms. Advances in Water Science, 1996, 7(4): 336-345. [谭维炎, 胡四一, 王银堂等. 长江中游洞庭湖防洪系统水流模拟——Ⅰ.建模思路和基本算法. 水科学进展, 1996, 7(4): 336-345.] |
| [18] |
Liu KL, Li ZJ, Yao C et al. Study on hydrology and hydraulic methods applied to the middle Huai River basin. Journal of Hydroelectric Engineering, 2013, 32(6): 5-10. [刘开磊, 李致家, 姚成等. 水文学与水力学方法在淮河中游的应用研究. 水力发电学报, 2013, 32(6): 5-10.] |
| [19] |
Wu ZP, Yang GL, Gan MH. Effection of lake-saving on calculation of complex river systems. Advances in Water Science, 2004, 15(5): 603-607. [吴作平, 杨国录, 甘明辉. 湖泊调蓄作用对河网计算的影响. 水科学进展, 2004, 15(5): 603-607.] |
| [20] |
Huaihe River Water Conservancy Commission of the Ministry of Water Resources ed. Report of design flood above Luoma lake in Yishusi River basin. Bengbu:Huaihe River Water Conservancy Commission of the Ministry of Water Resources, 1980. [水利部治淮委员会. 沂沭泗河流域骆马湖以上设计洪水报告. 蚌埠: 水利部淮河委员会, 1980. ]
|
 2018, Vol. 30
2018, Vol. 30 

