(2: 黄河流域水资源高效利用省部共建协同创新中心, 郑州 450046)
(3: 新疆兵团勘测设计院(集团)有限责任公司, 乌鲁木齐 830000)
(2: Collaborative Innovation Center for Efficient Utilization of Water Resources, Zhengzhou 450046, P.R.China)
(3: XPCC Surveying & Designing Institute (Group) Co., Ltd., Urumqi 830000, P.R.China)
黄河流域生态保护与高质量发展是国家重大战略之一[1],区域水资源—经济—生态系统是一类重要的复合系统,水资源的开发利用以生态和经济为基础[2-3]. 随着河南省社会经济高速发展,发展的不平衡不充分问题日益显现,水资源、经济发展和生态环境的矛盾尤为凸显[4-5]. 加强水资源管理,助力社会经济发展,贯彻新发展理念,实现生态效益和经济效益相统一,河南省黄河流域可持续发展、高质量发展成为关键.
近年来,复合系统耦合协调度研究逐渐成为研究热点. 焦士兴等[6]基于层次分析法和耦合协调度模型,对河南省城镇化与水资源系统的协调发展状况进行研究. 张晓昱等[7]引入耦合协调度模型和空间自相关指数,对城市经济—环境—社会3个系统进行相关性分析. 吴新静等[8]对河南省乡村人口—经济—土地系统的耦合协调发展进行研究,为实现河南省乡村振兴提供参考依据. 刘晏冰等[9]对城市人与自然协调度进行研究,为城市生态文明建设与可持续发展提供参考依据. 赵荣钦等[10]对区域“水—土—能—碳”耦合系统进行研究,提出了未来研究方向. Gao[11]等对甘肃省水环境和农村发展进行耦合协调度研究,研究结果对于进一步定量分析中国农村经济与水环境的相互作用与反馈机制有重要意义. 还有部分学者对耦合协调度进行预测,其中周成、凌立文和蔡文静等[12-14]应用GM模型预测不同区域耦合协调度,对区域未来发展进行分析. 韩瑞玲等[15]选择ARMA模型对沈阳经济区复合系统进行短期预测,为解决沈阳经济区经济发展与环境保护之间的矛盾提供参考依据. 曹青青[16]基于BP神经网络对西部地区复合系统耦合协调发展水平进行预测,为加快西部建设提供参考.
当前已有较多学者对复合系统耦合协调度进行研究,部分学者对耦合协调度进行预测,但预测方法较为单一. 因此本文以河南省黄河流域为研究区域,建立水资源—经济—生态系统评价指标体系,通过组合权重法确定各指标权重,构建河南省黄河流域水资源—经济—生态系统耦合协调评价模型,探究水资源、经济、生态3个子系统的发展状况,并通过ARIMA-GM组合模型预测河南省黄河流域未来5年的耦合协调度发展趋势,以期为河南省黄河流域资源集约利用与绿色协调高质量发展提供理论依据.
1 研究区概况与数据来源 1.1 研究区概况河南省(31°23′~36°22′N,110°21′~116°39′E)地处黄河流域中下游交汇处,是全国重要的综合交通枢纽及人流物流信息流中心. 黄河是中国的第二大河,流经河南省郑州市、开封市、洛阳市、安阳市、新乡市、濮阳市、三门峡市、济源市和焦作市共9座城市. 河南省黄河流域是黄河流经区域地形地貌特征最为特殊的区域,特殊的地理位置决定了其具有特殊性,如河水流速放缓、河道陡然变宽、泥沙淤积严重,导致历史上水患频仍、防洪压力极大. 此外,河南省黄河流域城市例如郑州、洛阳等重要的城市,人口众多,工商业发达,各种用水需求量极大,相对于河南省其他城市而言,面临着更加严峻的资源问题和生态问题[17].
1.2 数据来源对河南省水资源—经济—生态系统协调发展程度进行研究,其中所用到的数据来源于2000—2019年《中国统计年鉴》《河南省统计年鉴》《河南省水资源公报》《河南省环境状况公报》,2000—2019年河南省黄河流域各市级统计年鉴、水资源公报,2000—2019年《黄河水资源公报》等.
2 研究方法 2.1 指标体系构建河南省在整个黄河流域的发展中,站在非常重要的地理位置,本文以维护黄河生态安全,维持黄河健康生命为目标,依据指标构建的原则和方法[18-19],针对河南省黄河流域水资源—经济—生态耦合系统进行和谐程度量化分析. 其中,水资源子系统所选指标主要涉及水资源总量、资源开发利用水平两个方面;经济社会子系统主要考虑社会发展状况、地区经济水平;生态环境子系统则主要体现地区水生态、水环境状况. 综上,构建了水资源、经济、生态3个准则层,包含人均水资源量、年平均降雨量等共27个指标的综合评价指标体系. 具体如表 1所示.
| 表 1 河南省黄河流域水资源—经济—生态系统综合评价指标体系 Tab. 1 Comprehensive evaluation index system of water resources-economy-ecosystem of the Yellow River Basin in Henan Province |
目前关于耦合协调发展评价指标目标值的确定并无统一的方法,参考我国生态城市、高质量发展城市、生态文明城市在确定指标目标值时多采用未来某个时期的规划目标值、期望值或理想值,或采用某一典型城市或理想城市的数值作为标准[20]. 遵循指标选取原则:首选已有国际标准或国家标准的指标;参考我国生态城市,环保模范城市,高质量发展与新能源经济城市等相关指标值;采用专家咨询法. 根据《2020中国城市竞争力报告》中经济竞争力城市、高质量发展城市和宜居城市的评价结果及《新资源经济城市指数报告》中新资源经济城市评价结果,选取排名靠前的城市作为典型城市,最终选取4类8个城市,结果见表 2.
| 表 2 指标目标值确定参考城市 Tab. 2 Index target value to determine the reference city |
黄河流域高质量发展不仅要注重经济高质量发展,而且要注重社会、生态等方面的高质量发展,其内涵具有多维性、系统性、动态性和长期性[21]. 河南省黄河流域下一步发展的着力点是把河南省经济社会的发展跟生态文明保护结合起来,在经济发展中,更好地嵌入生态文明的理念[22-24]. 参考我国排名靠前的经济竞争力城市、可持续发展城市、宜居城市和新资源经济城市,结合河南省黄河流域发展的内涵和下一步发展着力点,确定河南省黄河流域水资源—经济—生态系统发展目标值,具体如表 3所示,由于篇幅有限,此处只展示部分指标目标值.
| 表 3 水资源—经济—生态耦合协调发展指标目标值 Tab. 3 Water resources-economy-ecological coupling coordinated development index target value |
本文在充分考虑不同因子之间的关联性、综合因子对最终结果的影响程度、单一权重法易出现误差的基础上,拟采用组合权重法计算河南省黄河流域20年的水资源—经济—生态系统27个指标的权重,通过主观与客观方法相结合的形式,使最终结果具有较强的可信度[25].
(1) 层次分析法
层次分析法主要以定性和定量因素组合的多准则决策方法,在结合专家打分的基础上,确定两两指标之间的耦合因素并筛选出相对重要的指标.
Yaahp软件是一种层次分析法可视化建模与计算软件[26]. Yaahp软件在操作过程中,判断矩阵值的输入有两种:一是可以选用判断矩阵形式,二是以文字描述形式输入,标度可选择e^(0/5)~e^(8/5)标度或1~9标度.
本文在Delphi法的基础上结合Yaahp软件进行权重计算,计算步骤为:1)利用Yaahp软件绘制层次结构模型;2)基于Delphi法,采用1~9等级标度法对指标进行两两比较,构造判断矩阵;3)一致性动态显示及检查;4)计算结果导出.
(2) 熵权法
利用熵权法确定权重主要是利用各指标的效用值来计算权重的大小,一般而言,效用值越高,则结果对评价的重要性也就越大. 熵权法的具体计算步骤如下:
1) 构造判断矩阵,使得该矩阵有n个样本、m个评价指标;
2) 将判断矩阵归一化处理,并得到归一化判断矩阵A,表达式为R=(Xji)nm;
3) 根据熵的定义,得到各指标的熵,即:
| $ H_{i}=-\frac{1}{\ln n}\left[\sum\limits_{i=1}^{n} f_{i j} \cdot \ln f_{i j}\right] $ | (1) |
式中,
4) 利用熵值计算评价指标的熵权:
| $ w_{i}=\frac{1-H_{i}}{m-\sum\limits_{i=1}^{m} H_{i}} $ | (2) |
式中,0≤wi≤1,
(3) 组合权重法确定最终权重
由层次分析法得到的权重ci记为主观权重,由熵权法得到的权重wi记为客观权重,将ci和wi进行线性组合,得到最终的权重值,记为Qi. 其中Qi=aCi+bwi,a和b分别表示主观权重和客观权重的相对重要程度,满足0≤a≤1,0≤b≤1且a+b=1. 由于主观法、客观法均无法达到实际情况的需求,但是通过主观赋值,往往更接近实际情况,因此,在利用组合权重法计算最终权重时,赋予主观权重的因子更大一些,客观权重的值相对小一些[27],本文a和b取值分别为0.6和0.4. 因此,得到组合权重的计算公式为Qi=0.6Ci+0.4wi,各指标最终权重值如表 4所示.
| 表 4 各指标最终权重值 Tab. 4 Final weight value of each indicator |
构建综合评价指数,即:
| $ \left\{\begin{array}{l} f(x)=\sum\limits_{i=1}^{m} \alpha_{i} \cdot x_{i} \\ g(y)=\sum\limits_{i=1}^{n} \beta_{i} \cdot y_{i} \\ h(z)=\sum\limits_{i=1}^{k} \gamma_{i} \cdot z_{i} \end{array}\right. $ | (3) |
式中,f(x)、g(y)、h(z)分别代表各子系统的综合效益;αi、βi、γi分别为各子系统中各指标的权重;xi、yi、zi分别为描述各指标的无量纲值[28].
本文涉及3个子系统,分别为水资源、经济、生态子系统,构建系统耦合度模型,即:
| $ C=\left\{\frac{f(x) \cdot g(y) \cdot h(z)}{\left[\frac{f(x) \cdot g(y) \cdot h(z)}{3}\right]^{3}}\right\}^{\frac{1}{3}} $ | (4) |
式中,C为耦合度,0≤C≤1. 当C处于0~0.3为低水平耦合阶段,处于0.3~0.5为颉颃阶段,处于0.5~0.8为磨合阶段,处于0.8~1.0为高水平耦合阶段.
根据水资源—经济—生态系统耦合度模型,可以计算出系统的耦合协调度D,本文认为水资源子系统、经济子系统和生态子系统同样重要,即α=β=γ=1/3,计算水资源—经济—生态系统综合评价指数T,即:
| $ D=\sqrt{C \cdot T} $ | (5) |
| $ T=\alpha \cdot f(x)+\beta \cdot g(y)+\gamma \cdot h(z) $ | (6) |
式中,C为耦合度,D为耦合协调度,T为耦合协调发展水平的综合评价指数,α、β、γ分别为各子系统的权重.
经济快速发展时期,往往伴随着资源消耗和环境污染,经济进入发达时期,会更加注重水资源和生态环境的保护. 本文在参考河南省黄河流域各城市水资源、经济发展、生态环境发展现状的基础上,结合前人经验[29-31],对耦合协调发展类型和标准进行划分,如表 5所示:
| 表 5 耦合协调发展类型和标准划分 Tab. 5 Coupling and coordinated development type and standard division |
GM模型、ARIMA模型是经典的预测模型[32-37],而ARIMA-GM组合模型是一种通过对GM模型和ARIMA模型拟合结果进行赋权加总而组合成新结果的预测模型,此方法具有趋利避害的特点[38-40]. 具体过程如下所示:
1) 用熵权法对各模型进行权重分配. 熵权法权重分配具体步骤上文2.2中已有,此处不再赘述.
2) 通过赋权加总,计算组合模型的拟合及预测结果. 具体公式如下所示:
| $ Y=\sum\limits_{i=1}^{2} w_{i} \cdot y_{i} $ | (7) |
式中,wi为GM模型或ARIMA模型的权重,yi为GM模型或ARIMA模型拟合预测结果,Y为GM-ARIMA组合模型的拟合预测结果.
3 现状分析与评价 3.1 现状值分析通过对河南省黄河流域内9个市水资源—经济—生态系统指标现状值与目标值对比分析,发现多数指标现状值与目标值的差距较大. 水资源短缺、人均GDP小、第二产业结构偏重和生态治理效果不显著是制约河南省黄河流域水资源—经济—生态系统协调发展的关键性因素.
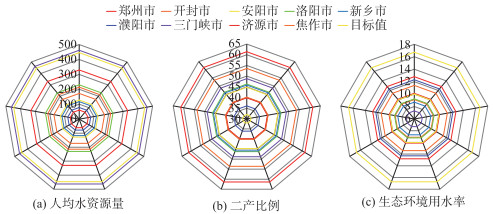
随着工业的快速发展,河南省黄河流域水资源供给与需求矛盾愈演愈烈. 2019年9个市人均水资源量、二产比例和生态环境用水率与目标值对比结果如图 1所示. 从图 1a可以看出,2019年,河南省黄河流域内9个市人均水资源量除三门峡市外,均未达到目标值,远低于全国人均水资源量. 其中,郑州市人均水资源量最低,为61.05 m3/人,原因是郑州市作为新兴城市,城市建设发展迅速,人口密度大,水资源总量相对较少. 图 1b可以看出,河南省是工业大省,工业是河南省经济发展的重点,2019年河南省黄河流域内9个市第二产业比例均高于目标值. 图 1c可以看出,流域内9个市生态环境用水率只有开封市、洛阳市、新乡市和三门峡市未超过目标值,分别为9.12%、9.23%、8.70%、7.30%,其余市均达到目标值.
|
图 1 2019年9个市人均水资源量(a)、二产比例(b)和生态环境用水率(c)与目标值的对比 Fig.1 Comparison of per capita water resources (a), secondary production ratios (b), and ecological environment water use rates (c) in 9 cities in 2019 with target values |
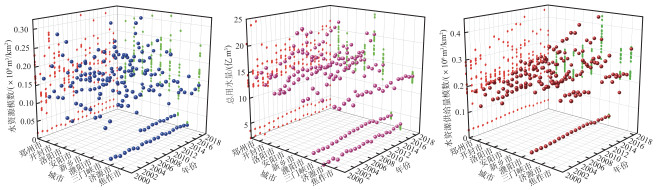
本文以水资源模数、总用水量和水资源供给量模数作为河南省黄河流域水资源状况的代表指标,以此分析河南省黄河流域各指标年际变化. 水资源模数代表了单位流域面积上的多年平均水资源量,可较好地反映一个地区的天然水资源条件. 总用水量是反映某一地区水资源利用情况的指标,可间接地反映出某一地区水资源需求量. 水资源供给量模数是某区域水资源供给量与土地面积的比值,可以较好地反映黄河流域地表水、地下水、蓄水工程和跨流域调水工程对水资源的供给能力. 选用这3个指标分析河南省黄河流域的水资源状况具有一定的现实意义. 不同市3个指标的年际变化如图 2所示.
|
图 2 2000—2019年9个市水资源模数、总用水量和水资源供给量模数的年际变化 Fig.2 Interannual changes in the modulus of water resources, total water consumption and water supply in 9 cities from 2000 to 2019 |
从河南省黄河流域内9个市水资源模数可以看出三门峡市水资源模数最大,2000—2019年平均值为0.09×106 m3/km2,这与三门峡市水资源充沛、土地面积相对较小有关. 济源市水资源模数平均值最小,为0.01×10 6m3/km2,原因是济源市山地较多,境内水资源有限,主要依靠境外产流,受国家水利工程调配和相关水利工程影响,分配给济源市的水资源量极为有限. 从总用水量年际变化可以看出,三门峡市与济源市总用水量多年值整体偏小. 其中,三门峡市总用水量少与其境内水库相对较多、人口密度小、年降雨量大有关. 济源市总用水量少是因为其境内水资源极其匮乏,人均水资源量很低. 从水资源供给量模数可以看出,三门峡市相对较低,年际变化较为平稳,在0.03×106~0.05×106 m3/km2之间.
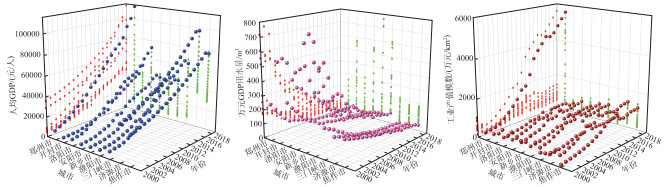
3.2.2 经济发展时空分布规律选择人均GDP、万元GDP用水量和工业产值模数作为河南省黄河流域经济发展的代表指标. 人均GDP常作为发展经济学中衡量经济发展状况的指标,是人们了解和把握一个国家或地区宏观经济运行状况的有效工具. 万元GDP用水量是将总用水量除以总GDP得出的,可以从侧面反映出某个区域水资源消耗量的多少. 工业产值模数是某区域工业总产值与该土地面积的比值,工业产值模数与区域经济发展水平呈正比. 因此,选用这3个指标分析河南省黄河流域的经济发展状况具有一定的现实意义. 不同市3个指标的年际变化如图 3所示.
|
图 3 2000—2019年9个市人均GDP、万元GDP用水量和工业产值模数的年际变化 Fig.3 Inter-annual changes in per capita GDP, water consumption per 10000 yuan of GDP, and industrial output value modulus in 9 cities from 2000 to 2019 |
从人均GDP年际变化来看,河南省黄河流域内9个市呈稳步增长趋势,其中郑州市人均GDP增长速度最快,从2000年的8965元/人增长到2019年的113139元/人,而焦作市人均GDP增长速度相对较慢. 从2000—2019年万元GDP用水量年际变化可以看出,新乡市、濮阳市、开封市和安阳市下降幅度较大,表明这些城市对当地的水资源优化利用起到了积极作用,但仍需改善. 郑州市工业产值模数从2000年到2019年急剧增长,从416.19万元/km2增长到5605.63万元/km2,河南省黄河流域其他城市均呈稳步增长趋势,这与郑州市建设国家中心城市有关.
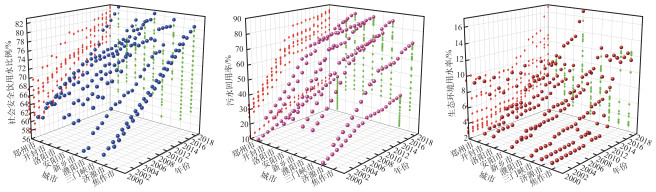
3.2.3 生态环境时空分布规律选用社会安全饮用水比例、污水回用率和生态环境用水率作为评价生态环境优劣的指标. 社会安全饮用水比例是饮用卫生达标水的人口占总人口的比例,社会安全饮用水比例间接反映某一区域的水环境状况. 污水回用率是污水回用量与污水回用量和直接排入环境的污水量的和的比值,可以直接反映某一地区水质、水量与生态环境状况. 生态环境用水率是生态环境用水量占总用水量的比例,可直接反映生态用水、环境用水情况,间接反映生态与环境功能. 因此,选用这3个指标分析河南省黄河流域的经济发展状况具有一定的现实意义. 不同市3个指标的年际变化如图 4所示.
|
图 4 2000—2019年9个市社会安全饮用水比例、污水回用率和生态环境用水率的年际变化 Fig.4 Inter-annual changes in the proportion of socially safe drinking water, sewage reuse rate and ecological environment water use rate in 9 cities from 2000 to 2019 |
河南省黄河流域内9个市社会安全饮用水比例均呈增长趋势,直至2019年郑州市社会安全饮用水比例最高,为82.78%,这与郑州市不断加强水环境治理有关. 9个市污水回用率2000—2019年在逐步升高,但与发达国家相比,仍相对较低. 从生态环境用水率来看,安阳市2019年生态环境用水率最高,达到16.73%,原因可能是早在2009年,安阳市委、市政府就决定从岳城水库调水满足生态环境用水,安阳市水利局与岳城水库签订了每年1.6亿m3的引供水协议,其中1.2亿m3为城市生态水,为安阳市水系景观建设提供了水源保障,有效改善了生态环境.
由3个子系统时空分布规律可知,各个城市间不同指标年际变化有明显差距,因此,相关部门需要考虑各个城市的空间复杂性、耦合协调发展程度等因素,有必要对河南省黄河流域沿线城市进行区域化管理.
3.3 现状评价——耦合协调度模型 3.3.1 综合评价指数时序分析运用河南省黄河流域水资源—经济—生态系统综合评价模型,计算得到河南省黄河流域2000—2019年综合评价指数(图 5).
|
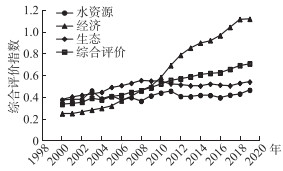
图 5 河南省黄河流域水资源—经济—生态系统历年综合评价指数 Fig.5 Evaluation index of water resources-economy-ecosystem of the Yellow River Basin in Henan Province over the years |
从图 5可以看出,河南省黄河流域水资源—经济—生态系统在2000—2019年综合评价指数呈升高趋势,从0.333升至0.711. 水资源子系统在2000—2019年整体波动相对较小,在个别年份有较明显的下降趋势. 经济子系统呈上升趋势,从2000年的0.247上升至2019年的1.125,从2005年开始呈大幅度上升趋势. 生态子系统较不稳定,综合评价指数2000—2008年呈逐渐升高趋势,2010年开始呈降低趋势,到2015年再次升高. 总体来看,河南省黄河流域水资源—经济—生态系统与各子系统2000—2019年呈上升趋势.
2003年黄河流域降水明显偏多,平均降水量为555.6 mm,折合降水总量为4417.0亿m3. 从降水量的地区分布看,三门峡至花园口区间最大. 2008年河南省黄河流域地表水水资源量减少,比多年平均值减少43.7%,其中伊洛河、沁河水系减幅超过50%. 2012年河南省人均水资源量相比于2011年大幅度下降. 2016年末河南省黄河流域的安阳—濮阳漏斗区面积扩大80 km2,漏斗中心地下水埋深增大1.84 m,这是由于地下水过量的开采,地下水收支平衡遭到破坏,从而导致地下水位持续下降. 综合以上原因,导致水资源子系统综合评价指数在2003年有明显上升趋势,2008、2012年有明显下降趋势,2016年有下降趋势.
经济子系统综合评价指数自2005年开始大幅度持续上升,是因为自河南省“十五”规划以来,河南省积极贯彻国家宏观调控政策,着力推进经济结构的战略性调整,河南省黄河流域综合经济实力显著增强,人均GDP由2005年的20018.8万元上升到2019年的68059.9万元,河南省完成了从农业大省向经济大省的转变.
直至2010年,河南省黄河流域人口多、底子薄、基础弱、发展不平衡尚未根本改变,环境形势依然严峻,基础能力相对滞后,加上此时期河南省黄河流域经济快速发展,环境保护体制机制仍不完善,生态子系统综合评价指数呈下降趋势. 2015年河南省黄河流域环境保护面临的形势依然十分严峻,资源环境约束趋紧,但相对于前几年,整体有所改善,河南省“十二五”环保规划实施总体进展良好. 河南省“十三五”环保规划期间,着力在构建生态环境预防体系上下功夫,效果较为明显,2019年河南省黄河流域生态子系统综合评价指数呈明显上升趋势.
3.3.2 耦合度和耦合协调度评价根据本文的研究方法,结合表 5对河南省耦合协调发展类型进行评价,评价结果如表 6、图 6所示:
| 表 6 河南省黄河流域水资源—经济—生态多指标评判结果 Tab. 6 Evaluation results of water resources-economy-ecology multi-indices of the Yellow River Basin in Henan Province |
|
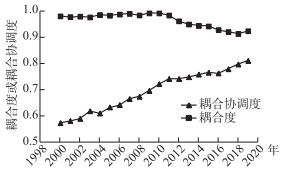
图 6 河南省黄河流域耦合度和耦合协调度 Fig.6 Coupling degree and coupling coordination degree of the Yellow River Basin in Henan Province |
从评价结果可以看出,2000—2019年河南省黄河流域耦合度虽一直处于高水平耦合阶段,但2011年前后开始呈降低趋势,是因为自1998年至今,河南省经济快速发展,但由于在经济发展初期,忽略了对生态治理、水资源的保护,2013年国家加大对生态及水资源的保护,但在保护力度上,尚未达到和经济子系统一样的发展速度,导致耦合度呈降低趋势. 2019年耦合度有上升趋势,说明生态治理效果已显现.
2000—2002年河南省黄河流域协调发展类型为勉强协调,进入2010年河南省黄河流域逐渐进入中级协调发展阶段,到了2019年河南省黄河流域的协调度总体发展进入良好协调期. 具体来看,从2000年到2019年河南省沿黄地区水资源—经济—生态结构配置逐年优化,受黄河流域水利工程开发与水资源治理工程的开展,河南省黄河流域实现了从勉强协调发展向良好协调发展的转变. 具体过程如下:由于1972—1999年黄河曾发生19次断流现象,严重破坏了沿黄流域的生态平衡,2001年12月31日,随着小浪底工程全部竣工之后,黄河流域的生态平衡开始正向发展,因此,2000—2002年河南省黄河流域的协调度低于0.6,处于勉强协调发展状态. 从2003年开始,到2009年前后,河南省黄河流域的水资源—经济—生态转变为初级协调发展状态,这是因为过度发展经济对水资源和生态环境亦造成了一定影响. 例如,在此期间,河南省第二产业内部制造业的比重逐年增加,2006年河南省第二产业内部制造业的比重为70.70%,高出全国第二产业内部制造业所占比重1.67%. 生态兴则文明兴,从2010年以后,河南省黄河流域的水资源—经济—生态逐步向中级协调发展转变,尤其是党的十八大以来,国家在生态环境和水资源优化配置方面做了大量工作,河南省进行深入贯彻落实. 例如河南省在大力推进污染防治持续改善生态环境等方面开展了大量工作,其中Ⅰ~Ⅲ类水质比例总体达到53%以上,完成营造林40000 hm2;在2019年河南省黄河流域的耦合协调发展度达到良好协调发展,这可能与全面推行河长制、构建水土流失防治体系、区域调水工程建设以及区域较大降雨量有关. 可见,在河南省黄河流域水资源极度紧缺条件下,各地区如何在经济高速发展的同时实现有效的环境保护,仍是今后的主要研究方向.
4 未来预测——ARIMA-GM模型 4.1 模型检验考虑到本研究所用的GM模型和ARIMA模型均属于短期预测模型,拟合预测时间过长会造成信息失真,本文将2000—2016年数据作为训练集,将2017—2019年数据作为测试集对模型效果进行检测. GM模型、ARIMA模型和ARIMA-GM组合模型检测结果如图 7所示.
|
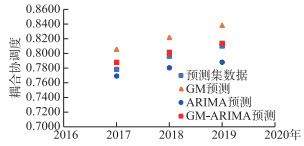
图 7 2017—2019年河南省黄河流域水资源—经济—生态系统预测模型检验图 Fig.7 Test chart of water resources-economy-ecosystem prediction model in the Yellow River Basin in Henan Province from 2017 to 2019 |
由图 7可以看出,ARIMA-GM模型预测结果与预测集数据最为接近,通过计算得出GM模型预测相对误差介于3.16%~3.49%之间,平均相对误差为3.37%;ARIMA模型预测相对误差介于1.15%~2.72%之间,平均相对误差为1.96%;ARIMA-GM组合模型预测相对误差介于0.45%~1.23%之间,平均相对误差为0.77%. 综上所述,ARIMA-GM组合模型预测效果较好,准确度较高.
4.2 保障方案本文主要从以下4个未来情景模拟2021—2025年河南省黄河流域水资源—经济—生态系统发展变化,以此确定最优保障方案,为今后河南省黄河流域水资源—经济—生态系统协调发展工作提供方向和理论依据.
情景1(现状):保持现有的发展状态,不采取任何措施,维持各指标变量值不变.
情景2:加强水资源保护. 减少工业用水比例每年1%,减少农业用水比例每年1%,减少生活用水比例每年1%,减少水资源供给量模数每年0.5%.
情景3:加强环境保护. 减少工业污染排放量每年2%,增加植被覆盖率每年1%,增加污水回用率每年1%,增加生态环境用水率每年1.5%.
情景4:综合方案2~3的所有改进措施,提高工业总产值增速8%,提高人均GDP增速8%,治污减污,加强环境保护等.
4.3 情景预测根据设定的未来发展情景,利用ARIMA-GM组合模型对4种情景进行模拟预测,计算河南省黄河流域水资源—经济—生态系统评价指标体系中各个指标2021—2025年共计5年的模拟预测值,未来4种情景下水资源—经济—生态耦合协调发展度见表 7.
| 表 7 河南省黄河流域未来4种情景下水资源—经济—生态系统耦合协调发展变化情况 Tab. 7 Changes in the coordinated development of water resources-economy-ecosystem coupling under the next four scenarios in the Yellow River Basin of Henan Province |
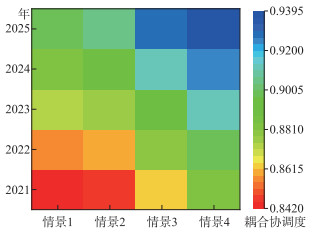
结合表 5,从表 7可以看出在维持现有发展程度下(即情景1),河南省黄河流域水资源—经济—生态系统耦合协调度由0.8424上升到0.8983,增长速率较为稳定,直至2025年仍未发展至优质协调发展类. 针对情景2状况,减少工业用水、农业用水、生活用水比例,减少水资源供给量模数的情况下,河南省黄河流域水资源—经济—生态系统耦合协调度相比于情景1有所提高,2025年发展至优质协调发展类. 针对情景3状况,减少工业污染排放量,增加植被覆盖率,增加污水回用率,增加生态环境用水率的情况下,河南省黄河流域水资源—经济—生态系统耦合协调度有较为明显的提高,2024年发展至优质协调发展类. 针对情景4状况,综合方案2~3的所有改进措施,提高工业总产值,提高人均GDP,治污减污,加强环境保护等措施同时实施的情况下,河南省黄河流域水资源—经济—生态系统耦合协调度发展趋势最好,2021年发展至良好协调发展类,2023年发展至优质协调发展类. 在情景4模式下,整体来看河南省黄河流域水资源—经济—生态系统未来发展态势良好,各子系统间协调发展较快,耦合协调度稳定升高. 因此,未来在保持现有发展优势的同时,需要不断关注水资源、经济和生态的发展,不断提高资源利用效率的同时,也要注重各子系统间的协调发展. 4个情景下2021—2025年河南省黄河流域水资源—经济—生态系统耦合协调度变化情况如图 8所示.
|
图 8 2021—2025年河南省黄河流域水资源—经济—生态系统耦合协调度变化 Fig.8 Changes in the coordination degree of water resources-economy-ecosystem coupling in the Yellow River Basin of Henan Province from 2021 to 2025 |
水资源,经济,生态三者相辅相成,在社会的发展过程中发挥着重要的作用. 本文对河南省黄河流域水资源—经济—生态系统进行探究,阐明了不同市水资源状况、经济社会发展程度以及生态环境演进规律,探索了河南省黄河流域内9座城市各指标的年际变化,构建了河南省黄河流域水资源—经济—生态系统耦合协调度模型进行综合评价,并对该复合系统未来发展进行预测.
1) 从河南省黄河流域水资源—经济—生态系统综合评价指数可知,河南省黄河流域水资源—经济—生态系统协调演化程度呈稳定上升状态. 水资源子系统综合评价指数整体波动较小,在2003年由于区域降水量过大呈上升趋势,2008、2012、2016年由于地表、地下水资源量减少,呈下降趋势;经济子系统综合评价指数呈上升状态,且2005年开始经济快速发展;生态子系统综合评价指数相对于其他两个子系统波动较大,2011年综合评价指数呈下降趋势,在2015年河南省开展“十二五”环保规划的情况下,河南省黄河流域生态子系统综合评价指数有了明显上升趋势.
2) 河南省黄河流域水资源—经济—生态系统一直处于高水平耦合阶段,表示各子系统间关联程度较好,且耦合协调度一直上升,至2019年耦合协调度过渡到良好协调发展类. 通过河南省黄河流域协调演化特征规律说明河南省黄河流域水资源—经济—生态系统总体保持良好趋势,且上升空间较大.
3) 基于ARIMA-GM模型预测的基础上,在情景4模式下发现,河南省黄河流域水资源—经济—生态系统呈稳定上升趋势,2023年发展至优质协调发展类,且发展空间、增长速度较大,未来应合理分配资源,提高各项资源利用效率,避免资源浪费,防止因城市高速发展而出现资源失衡.
5.2 讨论本文在研究内容方面,对河南省黄河流域进行整体性评价和耦合分析并进行分情景模拟预测,为河南省黄河流域的研究发展提供新的思路. 在研究方法方面,采用综合评价方法、耦合协调性分析方法对河南省黄河流域水资源—经济—生态耦合系统做出客观全面的评价及耦合研究,又利用ARIMA-GM短期预测模型对未来5年做出模拟预测,得出不同情景下耦合协调度发展状态,以期为河南省黄河流域高质量发展和生态文明建设提供理论参考和现实借鉴. 下面就研究过程中发现的问题以及对下一步研究的建议展开深入探讨.
5.2.1 系统协调评价于磊等[41]运用和谐量化模型对河南省水资源—能源—粮食耦合系统进行和谐评价,在其对水资源子系统进行分析时发现,2012年水资源子系统和谐程度最差,从2012年到2018年逐渐变好. 本文研究发现,河南省黄河流域水资源子系统综合评价指数在2003年有明显上升趋势,2008、2012年有明显下降趋势,2012—2018年总体呈上升趋势,在该研究水资源子系统分析中虽然与本文评价方法不同,但在相同年限内研究结果基本一致. 该研究在耦合协调度研究中认为各个子系统同等重要,权重平均分配,与本论文一致. 探究耦合协调评价子系统权重分配问题,经查阅相关文献,吴青松等、田培等、Tormal[42-44]考虑各系统的相对重要程度及协同发展的必要性,认为各子系统权重一样. 但在其他耦合协调度研究中,Zhu等[45]认为是要根据相关规划发展,咨询相关专家,按照区域具体情况分配权重,Wang等[46]认为各系统对协调发展的贡献不同,应根据相关人员对各子系统未来发展预测结果进行权重分配. 耦合协调评价子系统权重分配问题,对评价结果有一定影响,后续有待继续深入研究. 现有的指标体系在全面性方面有所欠缺,在下一步的研究中指标体系建立时,应本着黄河流域是一个生命共同体,统筹“山水林田湖草沙”,从宏观到微观,建立一个囊括自然、能源、社会、经济和环境等的指标体系.
5.2.2 系统未来预测通过对已有耦合协调度相关研究进行分析,发现在现有文章中,对黄河流域复合系统进行分情景模拟预测的较少,对河南省黄河流域水资源—经济—生态系统进行分情景模拟预测的文章几乎没有. 由于复合系统耦合协调度是随着各子系统变化不断发生改变的,影响其变化的因素众多,因此,本文在预测模型上选择短期预测模型. 在短期预测模型的选择上,本文选择目前应用较多的灰色预测模型和时间序列预测模型,但在模型检验时发现,二者与预测值相比,相对误差均较大. 探究其原因发现,由于灰色系统的理论体系目前还不完善,导致GM模型存在较多缺陷,GM模型的预测误差偏大是其主要缺陷之一[47-48]. 而时间序列模型适用范围不具有普遍性[49],当遇到外界发生较大变化,往往会有较大偏差[50]. 本文在模型检验时,发现ARIMA-GM组合模型对耦合协调度的预测精度比两种模型单一使用高,部分学者在其他领域的研究中,例如彭慧婷在发电量预测研究中、He在汇率预测的研究中和刘源在生活垃圾产量预测研究中也得出此类结果[51-53]. 但本文在建立ARIMA-GM模型时,由于资料搜集以及时间上的限制,模型的普遍适用性可能存在缺陷. 后期可通过资料收集,扩展完善模型,使得研究更具普适性.
| [1] |
Deng XZ, Yang KZ, Shan JJ et al. Urban agglomeration and industrial transformation and development in the Yellow River Basin. Journal of Natural Resources, 2021, 36(2): 273-289. [邓祥征, 杨开忠, 单菁菁等. 黄河流域城市群与产业转型发展. 自然资源学报, 2021, 36(2): 273-289. DOI:10.31497/zrzyxb.20210201] |
| [2] |
Lv T, Han WX. Chaos control of Ec-R-Ev system based on coordination. Systems Engineering-Theory & Practice, 2002, 22(3): 8-12. [吕彤, 韩文秀. 基于协调的区域"经济-资源-环境"系统混沌控制. 系统工程理论与实践, 2002, 22(3): 8-12. DOI:10.3321/j.issn:1000-6788.2002.03.002] |
| [3] |
Lv CM, Wu ZN. Emergy analysis for sustainable development assessment of regional water ecological-economics system. Systems Engineering—Theory & Practice, 2010, 30(7): 1293-1298. [吕翠美, 吴泽宁. 区域水资源生态经济系统可持续发展评价的能值分析方法. 系统工程理论与实践, 2010, 30(7): 1293-1298. DOI:10.12011/1000-6788(2010)7-1293] |
| [4] |
Huang CS, Geng LH, Yan B et al. Dynamic prediction and regulation of water resource carrying capacity: A case study on the Yellow River Basin. Advances in Water Science, 2021, 32(1): 59-67. [黄昌硕, 耿雷华, 颜冰等. 水资源承载力动态预测与调控——以黄河流域为例. 水科学进展, 2021, 32(1): 59-67.] |
| [5] |
Guo YY, Li SY, Liu R et al. Relationship between landscape pattern and water quality of the multi-scale effects in the Yellow River Basin. J Lake Sci, 2021, 33(3): 737-748. [郭羽羽, 李思悦, 刘睿等. 黄河流域多时空尺度土地利用与水质的关系. 湖泊科学, 2021, 33(3): 737-748. DOI:10.18307/2021.0310] |
| [6] |
Jiao SX, Wang AZ, Li QY et al. Study on coupling and coordinated development of urbanization and water resources in Henan Province. Water Resources Protection, 2020, 36(2): 21-26. [焦士兴, 王安周, 李青云等. 河南省城镇化与水资源耦合协调发展状况. 水资源保护, 2020, 36(2): 21-26.] |
| [7] |
Zhang XY, Qi J. Research on the coupling coordination transformation mechanism and spatial differentiation of regional economy, environment and society-a case study of Henan Province. Statistical Theory and Practice, 2020(5): 44-53. [张晓昱, 祁绩. 区域经济、环境与社会耦合协调转型机制及空间分异研究——以河南省为例. 统计理论与实践, 2020(5): 44-53.] |
| [8] |
Wu XJ, Li TS. Research on rural population-economy-land spatial agglomeration and coupling coordinated development under the background of rural revitalization—A case study of Henan. Hubei Social Sciences, 2019(6): 61-69. [吴新静, 李铜山. 乡村振兴背景下乡村人口—经济—土地空间集聚及耦合协调发展研究——以河南省为例. 湖北社会科学, 2019(6): 61-69. DOI:10.3969/j.issn.1003-8477.2019.06.010] |
| [9] |
Liu YB, Han BL, Liu JR et al. Harmonization of coupled human and natural systems in China urban area. Acta Ecologica Sinica, 2021, 41(14): 5578-5585. [刘晏冰, 韩宝龙, 刘晶茹等. 我国城市人与自然耦合系统的协调度. 生态学报, 2021, 41(14): 5578-5585. DOI:10.5846/stxb202002220306] |
| [10] |
Zhao RQ, Li ZP, Han YP et al. The coupling interaction mechanism of regional water-land-energy-carbon system. Acta Geographica Sinica, 2016, 71(9): 1613-1628. [赵荣钦, 李志萍, 韩宇平等. 区域"水—土—能—碳"耦合作用机制分析. 地理学报, 2016, 71(9): 1613-1628. DOI:10.11821/dlxb201609012] |
| [11] |
Gao X, Wang K, Lo K et al. An evaluation of coupling coordination between rural development and water environment in northwestern China. Land, 2021, 10(4): 405. DOI:10.3390/land10040405 |
| [12] |
Zhou C, Feng XG, Tang R. Analysis and forecast of coupling coordination development among the regional economy-ecological environment-tourism industry—A case study of provinces along the Yangtze economic zone. Economic Geography, 2016, 36(3): 186-193. [周成, 冯学钢, 唐睿. 区域经济—生态环境—旅游产业耦合协调发展分析与预测——以长江经济带沿线各省市为例. 经济地理, 2016, 36(3): 186-193.] |
| [13] |
Ling LW, Yu PX. Analysis and prediction of coupled coordination level of urbanization and eco-environment in Guangdong Province. Journal of Northwest A & F University: Social Science Edition, 2016, 16(4): 138-145, 154. [凌立文, 余平祥. 广东省城镇化与生态环境耦合水平分析与预测. 西北农林科技大学学报: 社会科学版, 2016, 16(4): 138-145, 154.] |
| [14] |
Cai WJ, Xia Y, Zhao XH. Analysis of coupled coordinated development and forecast of "ecological environment-economic development-urbanization" in five provinces of northwest China. Chinese Journal of Agricultural Resources and Regional Planning, 2020, 41(12): 219-227. [蔡文静, 夏咏, 赵向豪. 西北5省区"生态环境—经济发展—城镇化" 耦合协调发展及预测分析. 中国农业资源与区划, 2020, 41(12): 219-227. DOI:10.7621/cjarrp.1005-9121.20201225] |
| [15] |
Han RL, Tong LJ, Zhu SH et al. The coordinated development of economy and environment based on ARMA model in Shenyang economic zone. Scientia Geographica Sinica, 2014, 34(1): 32-39. [韩瑞玲, 佟连军, 朱绍华等. 基于ARMA模型的沈阳经济区经济与环境协调发展研究. 地理科学, 2014, 34(1): 32-39.] |
| [16] |
Cao QQ. A study on coupling coordination degree model and forecast of oil-economy-environment system—take the western region as an example[Dissertation]. Chengdu: Chengdu University of Technology, 2015. [曹青青. 石油—经济—环境系统耦合协调度模型及其预测研究——以西部地区为例[学位论文]. 成都: 成都理工大学, 2015. ]
|
| [17] |
Song GQ. The economic development path of Henan under the background of the national strategy of ecological protection and high-quality development of the Yellow River Basin. Yellow River. Loess. Yellow Race, 2020(15): 44-46. [宋冠群. 黄河流域生态保护和高质量发展国家战略背景下河南经济发展路径. 黄河黄土黄种人, 2020(15): 44-46.] |
| [18] |
Liu CG. Research on the construction of ecological planning index system and circular economy system[Dissertation]. Qingdao: Ocean University of China, 2004. [刘传国. 生态规划指标体系及循环经济体系构建研究——以临沂生态市规划为例[学位论文]. 青岛: 中国海洋大学, 2004. ]
|
| [19] |
Feng JH, Zhang LL, Tang M. Research on coupling coordination in ecology-economy-society system—taking Shaanxi Province as an example. Chinese Journal of Systems Science, 2021, 29(3): 92-96. [冯俊华, 张路路, 唐萌. 农业经济—生态—社会复合系统耦合协调发展研究——以陕西省为例. 系统科学学报, 2021, 29(3): 92-96.] |
| [20] |
Liang J. The research on the coordinative development between society-economic-water resource-water environment (sere) in Huaihe River basin of Henan[Dissertation]. Zhengzhou: Zhengzhou University, 2014. [梁静. 河南省淮河流域社会—经济—水资源—水环境(SERE)协调发展研究[学位论文]. 郑州: 郑州大学, 2014. ]
|
| [21] |
An SW, Li RP. Intension and promotion strategy of high-quality development in the Yellow River Basin. Reform, 2020(1): 76-86. [安树伟, 李瑞鹏. 黄河流域高质量发展的内涵与推进方略. 改革, 2020(1): 76-86.] |
| [22] |
Li JH. Problems in ecological protection and high-quality development of the Yellow River Basin in Henan and countermeasures. Science & Technology Economic Guide, 2020, 28(36): 124-125. [李建华. 河南黄河流域生态保护和高质量发展存在的问题及对策建议. 科技经济导刊, 2020, 28(36): 124-125.] |
| [23] |
Xinhua News Agency. When Xi Jinping hosted a symposium on ecological protection and high-quality development of the Yellow River Basin in Henan, he emphasized that we should work together to protect and coordinate to promote major governance and make the Yellow River a happy river that benefits the people. Yellow River, 2019, 41(10): 2-3. [新华通讯社. 习近平在河南主持召开黄河流域生态保护和高质量发展座谈会时强调共同抓好大保护协同推进大治理让黄河成为造福人民的幸福河. 人民黄河, 2019, 41(10): 2-3.] |
| [24] |
Yu SF. Basic follow and development countermeasures for ecological protection and high-quality development of the core demonstration area of the Yellow River Basin in Henan. Tourism Overview, 2021(2): 67-70. [于善甫. 河南黄河流域生态保护和高质量发展核心示范区建设的基本遵循与发展对策. 旅游纵览, 2021(2): 67-70.] |
| [25] |
Bao Yl, Tian B, Zhang Y et al. River health assessment in Xiongan New Area. Acta Ecologica Sinica, 2021, 41(15): 5988-5997. [鲍艳磊, 田冰, 张瑜等. 雄安新区河流健康评价. 生态学报, 2021, 41(15): 5988-5997. DOI:10.5846/stxb202004070817] |
| [26] |
Hu Y, Zhang Y. Based on Yaahp software to realize the risk analysis of BOT project capital structure under the AHP mode. Project Management Technology, 2011, 9(8): 27-31. [胡杨, 张毅. 基于Yaahp软件实现AHP模型下BOT项目资本结构风险分析. 项目管理技术, 2011, 9(8): 27-31. DOI:10.3969/j.issn.1672-4313.2011.08.004] |
| [27] |
Chen H. Research on key impact factors identification of water ecological health and harmony regulation in rivers controlled by sluices[Dissertation]. Zhengzhou: Zhengzhou University, 2016. [陈豪. 闸控河流水生态健康关键影响因子识别与和谐调控研究[学位论文]. 郑州: 郑州大学, 2016. ]
|
| [28] |
Li LX, Yang Q, Sun CC et al. Coupling coordinated evolution and forecast of tourism-urbanization-ecological environment: The case study of Chongqing, China. Mathematical Problems in Engineering, 2021, 1-15. DOI:10.1155/2021/7271637 |
| [29] |
Wang LC, Hou BD, Zhou YY et al. Research on the coupling coordinative degree in urban water-energy-food system. Hydro-Science and Engineering, 2021(1): 9-17. [王丽川, 侯保灯, 周毓彦等. 城市水-能源-粮食耦合协调发展研究. 水利水运工程学报, 2021(1): 9-17.] |
| [30] |
Diao YX, Zuo QT, Ma JX. Urbanization, water use level and their coupled coordination in the Yellow River Basin. Journal of Beijing Normal University: Natural Science, 2020, 56(3): 326-333. [刁艺璇, 左其亭, 马军霞. 黄河流域城镇化与水资源利用水平及其耦合协调分析. 北京师范大学学报: 自然科学版, 2020, 56(3): 326-333. DOI:10.12202/j.0476-0301.2020166] |
| [31] |
Wang H, Hu P. Key issues of ecological conservation in the Yellow River Basin from a water cycle perspective. Journal of Hydraulic Engineering, 2020, 51(9): 1009-1014. [王浩, 胡鹏. 水循环视角下的黄河流域生态保护关键问题. 水利学报, 2020, 51(9): 1009-1014.] |
| [32] |
Liu SF, Deng JL. The range suitable for GM (1, 1). Systems Engineering-Theory & Practice, 2000, 20(5): 121-124. [刘思峰, 邓聚龙. GM(1, 1)模型的适用范围. 系统工程理论与实践, 2000, 20(5): 121-124. DOI:10.3321/j.issn:1000-6788.2000.05.023] |
| [33] |
Zu XH, Yang CL, Wang YY. Performance prediction of successive supercharged diesel engines based on GM(1, 1) model and MATLAB GUI. Journal of Harbin Engineering University, 2015, 36(11): 1454-1458. [祖象欢, 杨传雷, 王银燕. 基于GM(1, 1)模型和MATLAB GUI的相继增压柴油机性能预测. 哈尔滨工程大学学报, 2015, 36(11): 1454-1458. DOI:10.11990/jheu.201408039] |
| [34] |
Wen LH. Grey system theory and application[Dissertation]. Harbin: Harbin Engineering University, 2003. [温丽华. 灰色系统理论及其应用[学位论文]. 哈尔滨: 哈尔滨工程大学, 2003. ]
|
| [35] |
Han C, Song S, Wang CH. A real-time short-term traffic flow adaptive forecasting method based on ARIMA model. Acta Simulata Systematica Sinica, 2004, 16(7): 1530-1532, 1535. [韩超, 宋苏, 王成红. 基于ARIMA模型的短时交通流实时自适应预测. 系统仿真学报, 2004, 16(7): 1530-1532, 1535. DOI:10.3969/j.issn.1004-731X.2004.07.042] |
| [36] |
Shadab A, Ahmad S, Said S. Spatial forecasting of solar radiation using ARIMA model. Remote Sensing Applications: Society and Environment, 2020, 20: 100427. DOI:10.1016/j.rsase.2020.100427 |
| [37] |
Li SY, Yang X, Li RR. Forecasting China's coal power installed capacity: A comparison of MGM, ARIMA, GM-ARIMA, and NMGM models. Sustainability, 2018, 10(2): 506. DOI:10.3390/su10020506 |
| [38] |
Li ZC, Liu S. Prediction comparison based on ARIMA model, grey model and regression model. Statistics & Decision, 2019, 35(23): 38-41. [李志超, 刘升. 基于ARIMA模型、灰色模型和回归模型的预测比较. 统计与决策, 2019, 35(23): 38-41.] |
| [39] |
Li SY, Li RR. Comparison of forecasting energy consumption in Shandong, China using the ARIMA model, GM model, and ARIMA-GM model. Sustainability, 2017, 9(7): 1181. DOI:10.3390/su9071181 |
| [40] |
Peng SG, Geng XH. Forecasting for import quantity and value of China's soybean based on ARIMA and GM (1, 1) models. Soybean Science, 2020, 39(4): 626-632. [彭世广, 耿献辉. 基于ARIMA和GM(1, 1)模型的中国大豆进口量及进口额预测. 大豆科学, 2020, 39(4): 626-632.] |
| [41] |
Yu L, Guojia H, Wang HL. Harmonious evaluation of the coupling system of regional water resources, energy and food. South-to-North Water Transfers and Water Science & Technology, 2021, 19(3): 437-445. [于磊, 郭佳航, 王慧丽. 区域水资源-能源-粮食耦合系统和谐评价. 南水北调与水利科技: 中英文, 2021, 19(3): 437-445.] |
| [42] |
Wu QS, Ma JX, Zuo QT et al. Quantitative analysis on harmony degree of water resources-economic society-ecological environment coupling system in the Tarim River Basin. Water Resources Protection, 2021, 37(2): 55-62. [吴青松, 马军霞, 左其亭等. 塔里木河流域水资源-经济社会-生态环境耦合系统和谐程度量化分析. 水资源保护, 2021, 37(2): 55-62.] |
| [43] |
Tian P, Wang JY, Hua W et al. Temporal-spatial patterns and coupling coordination degree of water resources carrying capacity of urban agglomeration in the middle reaches of the Yangtze River. J Lake Sci, 2021, 33(6): 1871-1884. [田培, 王瑾钰, 花威等. 长江中游城市群水资源承载力时空格局及耦合协调性. 湖泊科学, 2021, 33(6): 1871-1884. DOI:10.18307/2021.0621] |
| [44] |
Tomal M. Analysing the coupling coordination degree of socio-economic-infrastructural development and its obstacles: The case study of Polish rural municipalities. Applied Economics Letters, 2021, 28(13): 1098-1103. DOI:10.1080/13504851.2020.1798341 |
| [45] |
Zhu H, Zhu JS, Zou Q. Comprehensive analysis of coordination relationship between water resources environment and high-quality economic development in urban agglomeration in the middle reaches of Yangtze River. Water, 2020, 12(5): 1301. DOI:10.3390/w12051301 |
| [46] |
Wang Y, Chen XH, Sun PJ et al. Spatial-temporal evolution of the urban-rural coordination relationship in northeast China in 1990-2018. Chinese Geographical Science, 2021, 31(3): 429-443. DOI:10.1007/s11769-021-1202-z |
| [47] |
Li K. The application study of optimized grey prediction models[Dissertation]. Shanghai: Shanghai University of Finance and Economics, 2020. [李凯. 灰色预测模型的优化及其应用研究[学位论文]. 上海: 上海财经大学, 2020. ]
|
| [48] |
Li L, Li XC. Optimization algorithm and application of grey GM(1, 1) model. Statistics & Decision, 2019, 35(13): 77-81. [李丽, 李西灿. 灰色GM(1, 1)模型优化算法及应用. 统计与决策, 2019, 35(13): 77-81.] |
| [49] |
Cao JB, Zhou RJ, Deng XH et al. Wind power forecast considering differential times of optimal ARIMA model. Proceedings of the CSU-EPSA, 2019, 31(1): 105-111. [曹俊波, 周任军, 邓学华等. 考虑优化ARIMA模型差分次数的风功率预测. 电力系统及其自动化学报, 2019, 31(1): 105-111. DOI:10.3969/j.issn.1003-8930.2019.01.017] |
| [50] |
Escudero P, Alcocer W, Paredes J. Recurrent neural networks and ARIMA models for euro/dollar exchange rate forecasting. Applied Sciences, 2021, 11(12): 5658. DOI:10.3390/app11125658 |
| [51] |
Peng HT. Research of power generation forecast based on the GM-ARIMA model[Dissertation]. Lanzhou: Lanzhou University, 2014. [彭慧婷. 基于GM-ARIMA模型的发电量预测研究[学位论文]. 兰州: 兰州大学, 2014. ]
|
| [52] |
H eT, Jin LQ. Research on forecasting exchange rate based on ARIMA-GM combined model of inverse transform. Advances in Applied Mathematics, 2019, 8(4): 595-601. DOI:10.12677/aam.2019.84066 |
| [53] |
Liu Y. Research of Chengdu domestic waste output forecast based on GM-ARIMA model[Dissertation]. Chengdu: Southwest Jiaotong University, 2016. [刘源. 基于GM-ARIMA模型的成都市生活垃圾产量预测研究[学位论文]. 成都: 西南交通大学, 2016. ]
|
 2022, Vol. 34
2022, Vol. 34 

